后缀表达式

什么是后缀表达式？

在计算机科学和数学领域，表达式求值是一项基本且频繁的任务。我们熟知的中缀表达式（如 7 + 15 ∗ 1 + 4 ∗ 1）直观易读，但在计算机处理时却需要复杂的栈或递归算法来解析。相比之下，后缀表达式（又称为逆波兰表示法）则更为简洁。

后缀表达式是一种将运算符放置在操作数之后的表示法。比如，中缀表达式 5 + 3 ∗ 2 在后缀形式下写作 5 3 2 ∗ + 。在这一表示法中，每个运算符紧跟着它作用的所有操作数，消除了括号的需要，简化了计算规则。

后缀表达式的优点

简化解析：后缀表达式无需考虑运算符优先级和括号，可以直接通过栈实现简单高效的计算。
直接计算：遵循遇到操作数入栈，遇到运算符弹出栈顶两个操作数计算并将结果入栈的原则，直至表达式结束。
易于实现：后缀表达式的算法实现相对简单，减少了编程复杂度

中缀转后缀

• 我们利用栈将中缀表达式转换为后缀表达式。
• 遍历中缀表达式，如果遇到数字，直接将其添加到输出队列的末尾。
• 如果遇到的是左括号 (，直接将其压入操作符栈。
• 如果遇到的是右括号 )，则不断地从操作符栈顶弹出操作符并加入输出队列，直到遇到左括号 (（左括号不加入输出队列，直接丢弃），这样做的目的是将括号内的表达式处理完毕。
• 对于其他操作符（如 +, -, *, /），需要与栈顶的操作符比较优先级：
• 如果栈顶操作符优先级更低或栈为空，则将当前操作符压入栈。
• 如果当前操作符优先级不低于栈顶操作符（如乘除优先于加减），则持续从栈顶弹出操作符加入输出队列，直到栈顶的操作符优先级低于当前操作符，然后将当前操作符压入栈。
• 遍历完整个中缀表达式后，如果操作符栈中仍有剩余操作符，将它们全部弹出并加入输出队列。

示例：

假设有一个中缀表达式：3 + 4 * 2 - (10 / 5)

转换过程如下：

遇到 3，输出队列变为 3。

遇到 +，压入操作符栈。

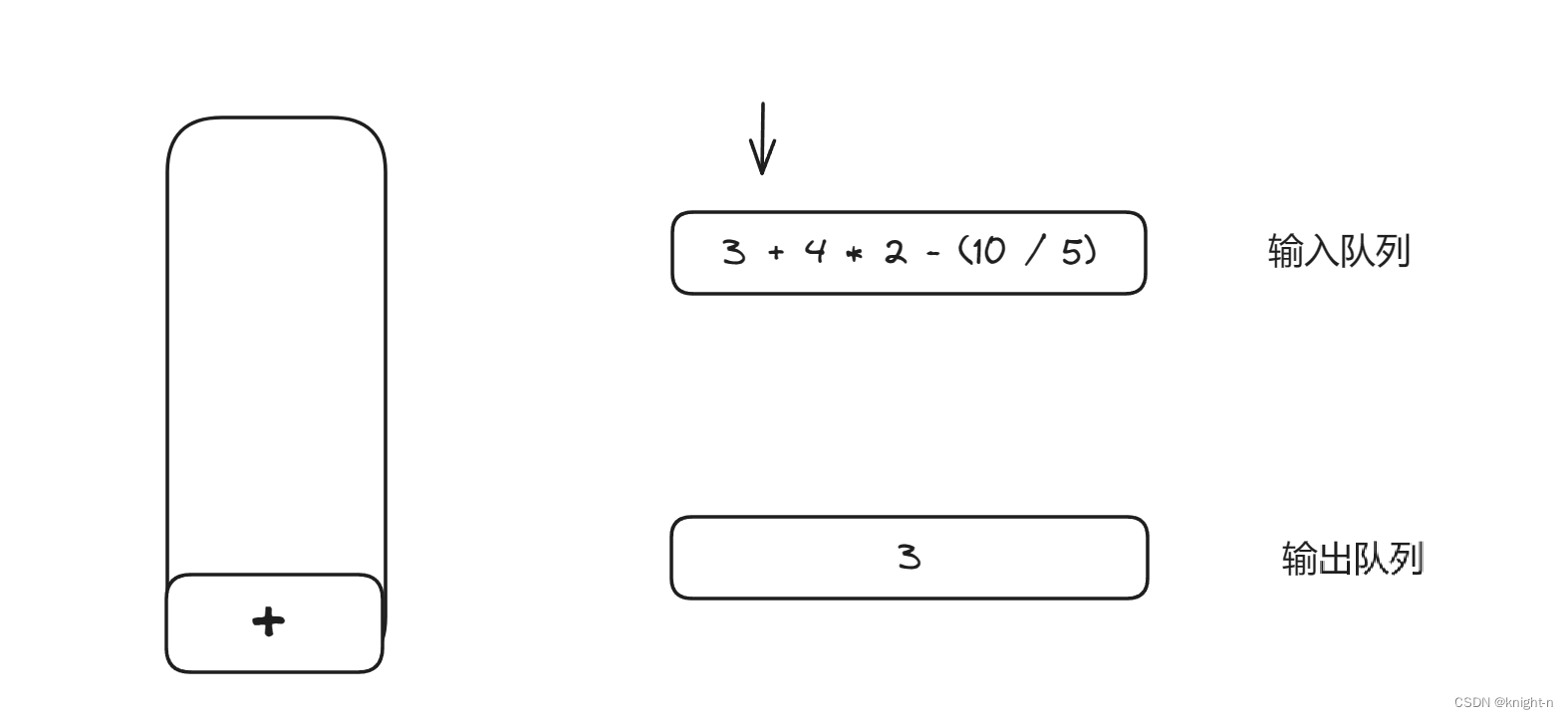
遇到 4，输出队列变为 3 4。

遇到 *，由于 * 的优先级高于 +，将 * 压入栈。

遇到 2，输出队列变为 3 4 2。

遇到 -，此时栈顶为 *，优先级不低于 -，故先弹出 * 加入输出队列，然后将 - 压入栈，输出队列变为 3 4 2 *。

遇到左括号 (，压入栈。

遇到 10，输出队列变为 3 4 2 * 10。

遇到 /，压入栈。

遇到 5，输出队列变为 3 4 2 * 10 5。

遇到右括号 )，弹出栈顶直到左括号，输出队列变为 3 4 2 * 10 5 /。

遍历结束，栈中剩余 -，弹出加入输出队列，最终输出队列为：3 4 2 * 10 5  /  - +。

后缀表达式的运算 

后缀表达式的运算也通过栈进行。方法如下：

• 左到右扫描后缀表达式：每次遇到一个元素，根据以下规则处理：
• 如果是操作数（数字），直接将其压入栈顶。例如，遇到数字 5，直接将其压入栈中。
• 如果是运算符（如 +, -, *, /），从栈顶弹出两个操作数（栈顶元素作为第二个操作数，次栈顶元素作为第一个操作数），对它们进行相应的运算，然后将运算结果压回栈顶。
• 遍历完整个表达式后，栈顶剩下的唯一元素就是整个后缀表达式的计算结果。

示例：

我们用上面算出的后缀表达式进行演示：3 4 2 * 10 5  /  - +。

遍历后缀表达式：

遇到 3，压栈 → 栈：[3]

遇到 4，压栈 → 栈：[3, 4]

遇到 2，压栈 → 栈：[3, 4, 2]

遇到 *（乘法），弹出 2 和 4，计算 4 * 2 = 8，压栈 → 栈：[3, 8]

遇到 10，压栈 → 栈：[3, 8, 10]

遇到 5，压栈 → 栈：[3, 8, 10, 5]

遇到 /（除法），弹出 5 和 10，计算 10 / 5 = 2，压栈 → 栈：[3, 8, 2]

遇到 -（减法），弹出 2 和 8，计算 8 - 2 = 6，压栈 → 栈：[3, 6]

遇到 +（加法），弹出 6 和 3，计算 3 + 6 = 9，压栈 → 栈：[9]

遍历完成，栈中剩下 9，这是后缀表达式 3 4 2 * 10 5 / - + 的计算结果。

代码实现

// 辅助函数确定操作符的优先级
int precedence(char op) 
{
    if (op == '*' || op == '/') return 2;
    if (op == '+' || op == '-') return 1;
    return 0; // 无效操作符的默认优先级
}

// 辅助函数判断字符是否为操作符
bool isOperator(char c) 
{
    return c == '+' || c == '-' || c == '*' || c == '/';
}


std::string infixToPostfix(const std::string& infixExp) 
{
    std::stack<char> operators;
    std::stringstream output;
    for (char c : infixExp) 
    {
        if (isdigit(c)) 
        {
            output << c; // 直接输出数字
        } 
        else if (isOperator(c)) 
        {
            while (!operators.empty() && precedence(operators.top()) >= precedence(c)) 
            {
                output << ' ' << operators.top();
                operators.pop();
            }
            operators.push(c);
        } 
        else if (c == '(') 
        {
            operators.push(c);
        } 
        else if (c == ')') 
        {
            while (!operators.empty() && operators.top() != '(') 
            {
                output << ' ' << operators.top();
                operators.pop();
            }
            if (!operators.empty() && operators.top() == '(')
                operators.pop(); // 弹出左括号，但不输出
        }
    }
    // 处理剩余的操作符
    while (!operators.empty())
    {
        output << ' ' << operators.top();
        operators.pop();
    }
    return output.str();
}