Leetcode239 - 滑动窗口最大问题（单调栈）学习笔记 Java

概述：

单调队列就是在普通队列的基础上要求队列的整体是单调递增或递减的，对于一个单调队列，如果我们要在此队列尾部增加任意一个元素，都要判断此元素加入队列后是否能使原队列保持单调的特性，如果不影响即直接添加，如果原来队列的单调性改变，则需要根据原队列是单调增或减来移除比待添加元素大或小的所有元素，直到添加后仍不改变单调性为止，而从移除的poll方法则没有限制。

如一个单调递减队列{7，5，3，1}，要添加一个元素6，则需要将5，3，1全部移除后再在尾部添加6，由此可见，此队列创建应当是个双端队列。

代码实现：

/**
 * <h3>单调递减队列</h3>
 * 队列中的元素都是单调递减的
 * 如果要添加一个元素，那么队列中所有比这个元素小的都要移除
 */
public class MonotonicQueue {

    private LinkedList<Integer> deque = new LinkedList<>();  //创建一个双端队列

    public Integer peek() {
        return deque.peekFirst();  //从头部获取元素，但不移除
    }

    public void poll() {
        deque.pollFirst();  //获取且移除
    }

    // 6 5 4 2 1    <= 3
    public void offer(Integer t) {
        while (!deque.isEmpty() && deque.peekLast() < t) {  //队列尾部的元素要比添加的元素小
            deque.pollLast();  //不断循环，从队列的尾部移除这些元素
        }
        deque.offerLast(t);  //再将t加入
    }

    @Override
    public String toString() {
        return deque.toString();  //打印队列
    }

    public static void main(String[] args) {
        MonotonicQueue q = new MonotonicQueue();
        for (int i : new int[]{1, 3, -1, -3, 5, 3, 6, 7}) {
            q.offer(i);
            System.out.println(q);
        }

    }
}

运用单调队列的性质，我们可以解决如下问题：

模拟题意：

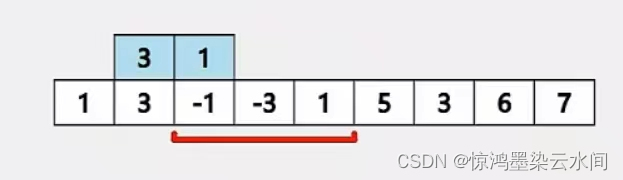
红色框为大小为 3 的滑动窗口，每次可以向右移动一格，本题其实就是要求在窗口内数字凑满三个的时候计算这三个数字的最大值，每移动一次就将最大值记录一次。

第一次移动只有一个数字无需考虑最大值并输出，直到窗口移动到 -1 处，此时窗口被填满，其最大值为 3 ，将 3 记录下来并继续右移。

同理，窗口一直右移，每次记录最大值，直到移动到最后一个元素，求解完毕。

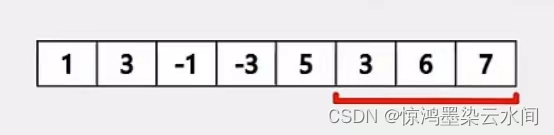
对于单调队列，不难发现，我们只需要每次在窗口右移的时候就把这个元素加入到队列当中，单调队列队头的元素就是最大的即滑动窗口的最大值。

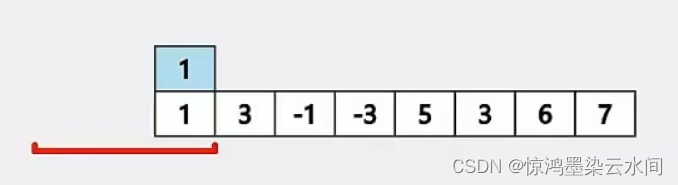
一开始我们将单调队列中加入元素 1：

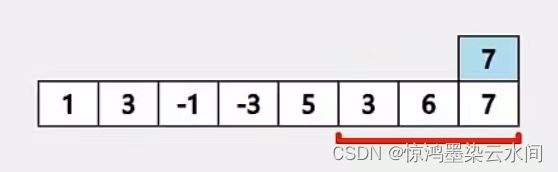
接着向右移动，加入 3 ，但是加入 3 后就不满足单调性了，则将 1 移除，再进行添加。后面再移动，-1 比 3 小，跟在 3 后面，继续右移，遇到大的就移除前面比其小的，如此往复就能求得答案。

整体思路：

1. 创建一个单调队列（前面的实现），创建一个集合收集结果

2. 写外层循环，检查队列头部元素，超过滑动窗口范围要移除

3. 获取输入的 k ，在此范围内拿到队列头部的元素，通过当前的索引 i  -  滑动窗口的范围k  即可得到滑动窗口外上一个元素。如果发现和队首元素相同，说明这个队首元素超过范围了，将其移除

如果不加 if 判断则第三次输出的结果就是错误的 3 

 

注意点：不能通过判断队列中的元素个数超过了窗口的最大范围而移除元素，这可能导致将队列中比新加入的元素小的都移除了，导致队列中的元素个数小于3，如下例子：

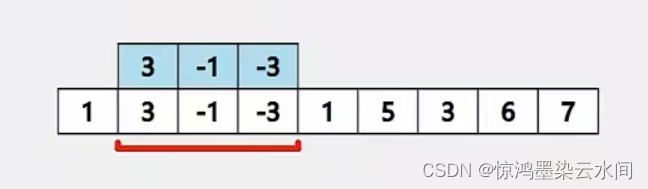
移动后：

发现也会拿到之前窗口外的元素，因此也是错误的

4. 移除并添加，如果直接从 0 开始获取最大值，那么前面就会出现不满 k 个的元素进行获取头部，应该从 k - 1 开始(窗口满了)才获取最大值

5. 拿到队列头部的元素加到集合中

代码实现（已将注释写好）：

/**
 * <h3>滑动窗口最大值 - 单调队列</h3>
 */
public class SlidingWindowMaximumLeetcode239 {

    // 每次向单调递减队列加入元素，队头元素即为滑动窗口最大值
    static int[] maxSlidingWindow(int[] nums, int k) {
        MonotonicQueue queue = new MonotonicQueue();  //创建一个单调队列
        List<Integer> list = new ArrayList<>();  //创建一个集合收集结果
        for (int i = 0; i < nums.length; i++) {
            // 检查队列头部元素，超过滑动窗口范围要移除
            if (i >= k && queue.peek() == nums[i - k]) {
            //i >= k: 保证在滑动窗口范围内
            //queue.peek() == nums[i - k]:拿到队列头部的元素，通过当前的索引i - 滑动窗口的范围k 即可得到滑动窗口外的上一个元素，如果发现和队首元素相同，说明这个队首元素超过范围了，将其移除

            //注意：不能通过判断队列中的元素个数超过了窗口的最大范围而移除元素，这可能导致将队列中比新加入的元素小的都移除了，导致队列中的元素个数小于3，就会拿到窗口外的元素
                queue.poll();  //移除
            }
            int num = nums[i];  //拿到第i个元素
            queue.offer(num);  //将第i个数字添加到队列中
            if (i >= (k - 1)) {  //如果直接从0开始获取最大值，那么前面就会出现不满k个的元素进行获取头部，应该从 k - 1 开始(窗口满了)才获取最大值
//                System.out.println(queue.peek());
                list.add(queue.peek());  //拿到队列头部的元素加到集合中
            }
        }
        return list.stream().mapToInt(Integer::intValue).toArray();
        //通过流的方式，Integer::intValue通过包装类型的int转化成基本类型的int，再转成数组
    }

    public static void main(String[] args) {
        System.out.println(Arrays.toString(
                maxSlidingWindow(new int[]{1, 3, -1, -3, -4, 5, 3, 6, 7}, 3))
        ); //[3, 3, 5, 5, 6, 7]
//        System.out.println(Arrays.toString(maxSlidingWindow(new int[]{7, 2, 4}, 2))); // [7, 4]
//        System.out.println(Arrays.toString(maxSlidingWindow(new int[]{1, 3, 1, 2, 0, 5}, 3))); // [3, 3, 2, 5]
//        System.out.println(Arrays.toString(maxSlidingWindow(new int[]{-7, -8, 7, 5, 7, 1, 6, 0}, 4))); // [7, 7, 7, 7, 7]
    }
}