进 制 转 换

一、进制分类

二进制（B）

十进制（D）

八进制（O）

十六进制（H）

括号中的字母表示用来代表该数为什么类型的进制

二、进制转换

1.十进制

1）n进制 -> 十进制  （加权展开求和）

1.1 、二进制转十进制

1110  1010（B）

1×2⁷+1×2⁶+1×2⁵+0×2⁴+1×2³+0×2²+1×2¹+0×2⁰ = 128+64+32+8+2=234

1.2、八进制转十进制

352（O）

3×8²+5×8¹+2×8⁰=192+40+2=234

1.3、十六进制转十进制

（十六进制中 ，0-9正常排序，10-16分别用A BCDEF表，例如：12DE则为 12 13 14）

EA（H）

14×16¹+10×16⁰=224+10=234

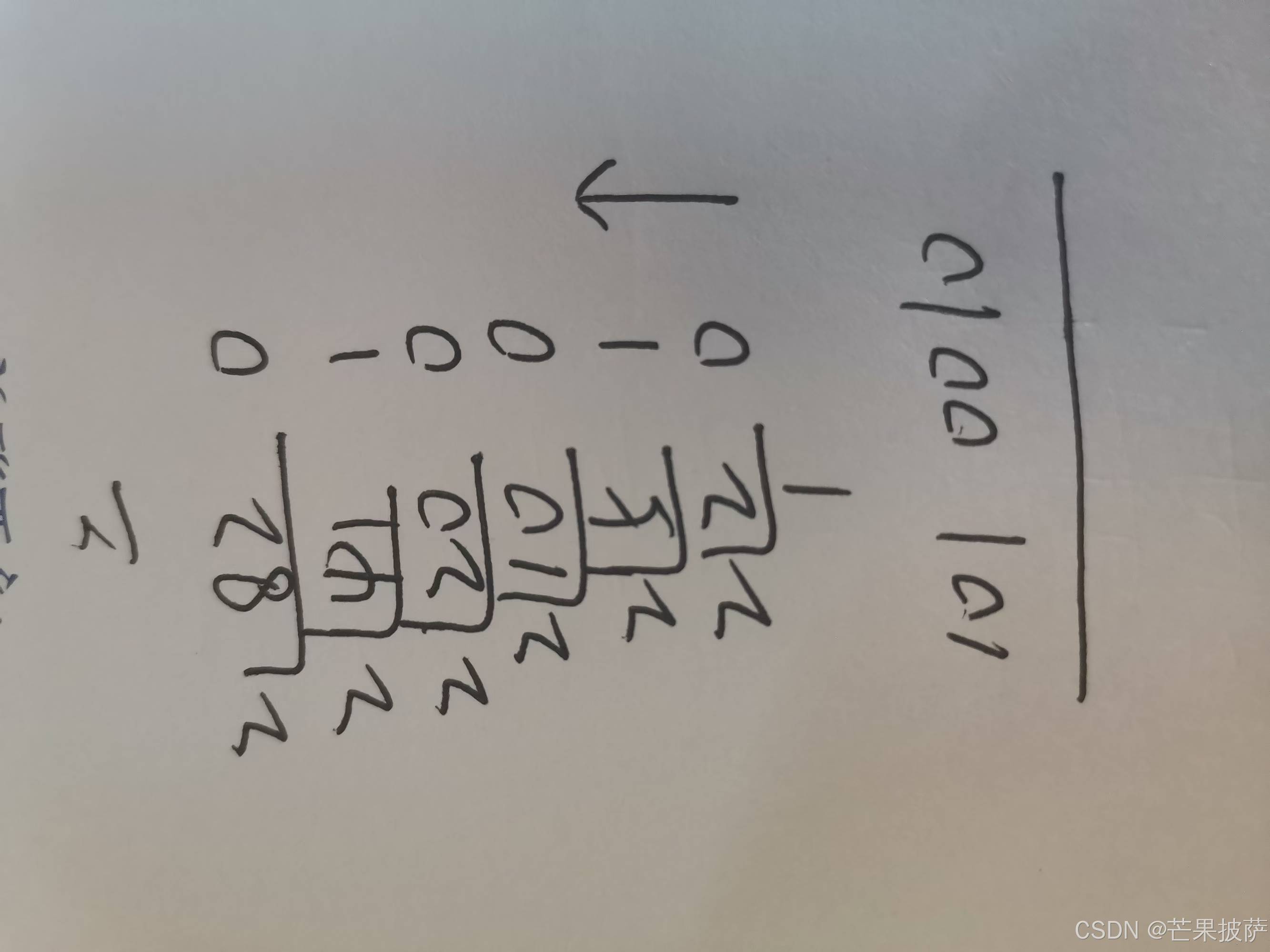
2）十进制-> n进制  除n反序倒余法

1.1 十进制转二进制

1.2十进制转八进制

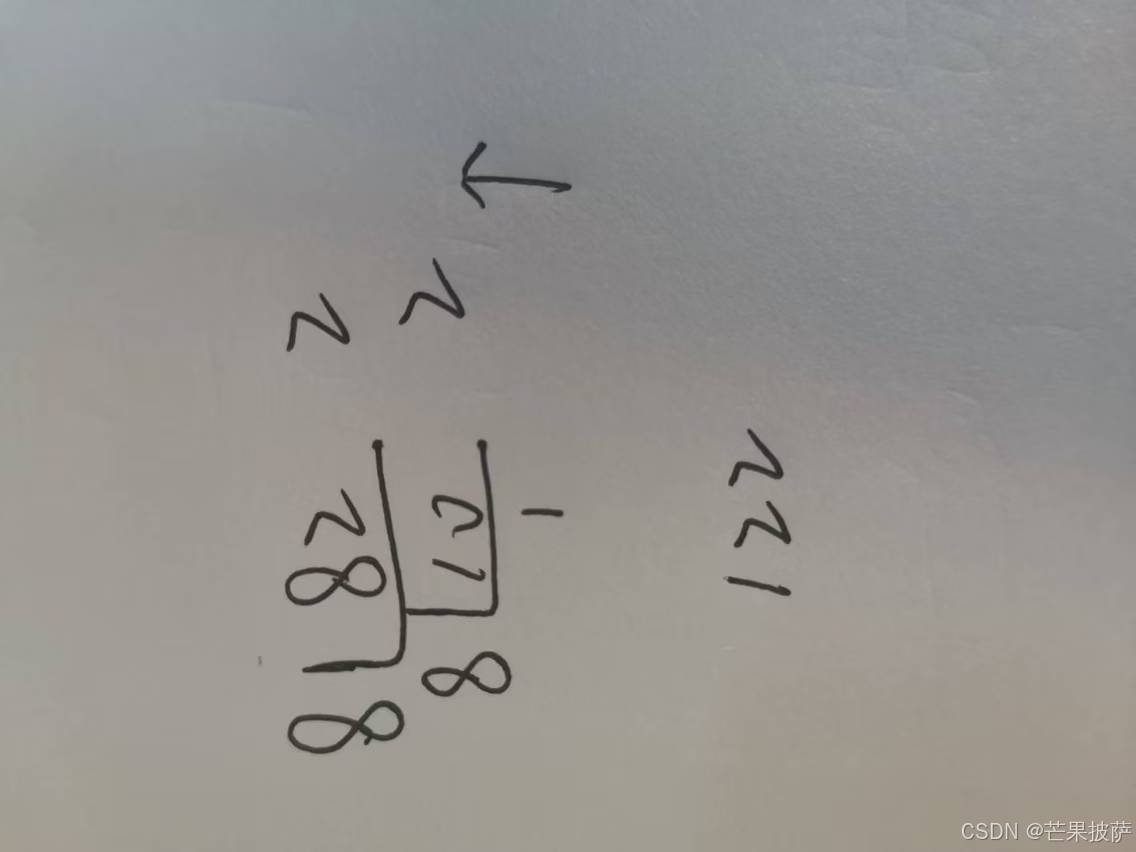
1.3十进制转十六进制

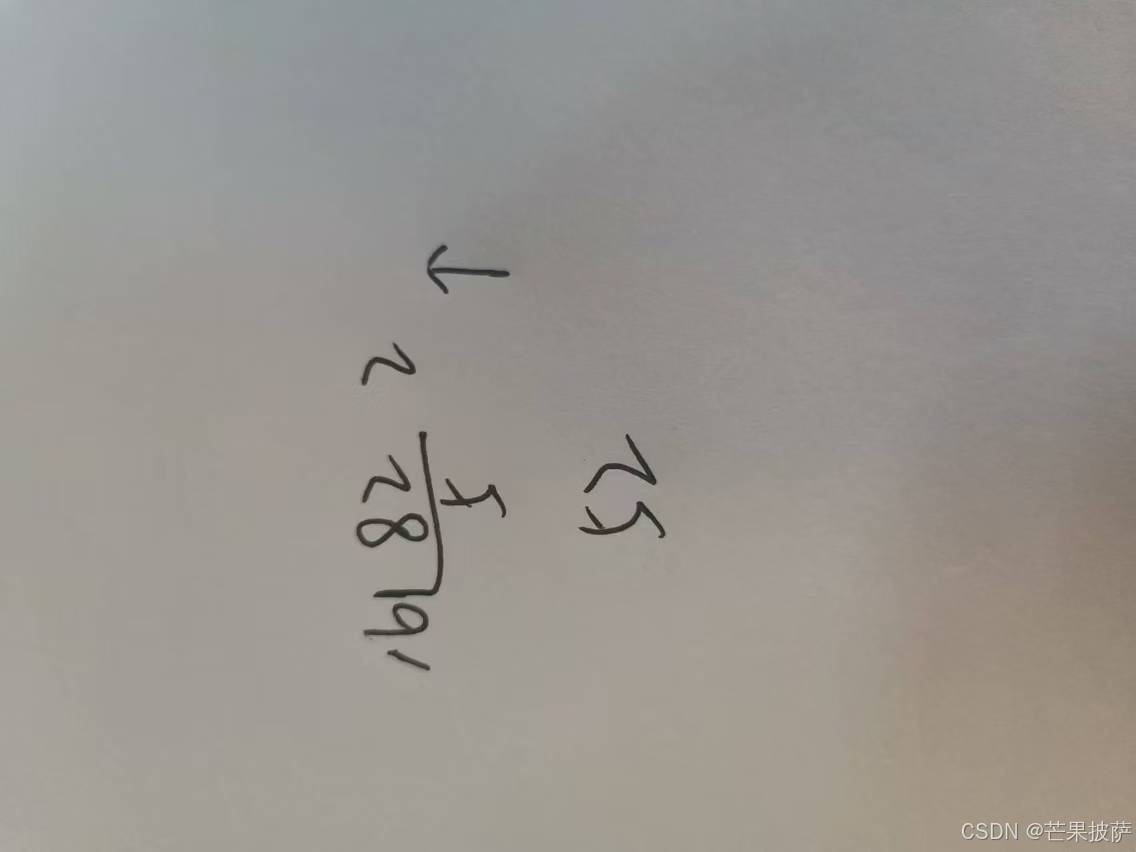
2.二进制

2.1、八进制转二进制  -> 一位八进制等于三位二进制

举例：

352（O）

一个八进制等于三位二进制，所以每个数扩展为三位，即

_ _ _  _ _ _  _ _ _（三位表示一个数）

 ↑       ↑       ↑

 3       5       2

3 =  0  +  2¹ + 2⁰  --> 011

5 =  2² + 0  + 2⁰   --> 101

2 =  0 + 2¹ + 0     -->010

从高位到低位 011101010，第一位的0可以去掉，即为1110 1010

2.2、十六进制转二进制 -> 一位十六进制等于四位二进制

举例

EA（H）

一位十六进制等于四位二进制，每位数扩展为四位，即

_ _ _ _    _ _ _ _（四位表示一个数）

   ↑          ↑

  E           A

E = 2³+2²+2¹+0  -->1110

A= 2³+0+2¹+0    -->1010

从高位往低，即为 1110 1010

三、进制加减法

1.加法（逢n进1）

举例：

239（D）+1=240 

这个过程中逢十进1，正常的加法，因此各种进制做加法也是如此，都是逢n进1

二进制：

   1011  1111

+                  1

————————

    1100 0000

2.减法（借1当n）

举例：

234（D）- 5 = 229

这个过程中借1当10，正常的减法，因此另外的进制也是如此计算