一.查找的基本概念
查找是由同一类型的数据元素(或记录)构成的集合。由于集合中数据元素存在着松散的关系,因此查找表是一种应用灵便的结构
1.关键字
主关键字:可唯一标识一个记录的关键字是主关键字
次关键字:相反,用以识别若干记录的关键字是次关键字
查找算法的评价指标:
2.关键字的平均比较次数,也称平均比较长度ASL
3.分类
静态查找表:仅作查询(检索)操作的查找表
动态查找表:作插入和删除操作的查找表
二.线性表的查找----ASL=(n+1)/2
1.顺序查找(线性查找)
顺序表或线性链表表示的静态查找表
表内元素之间无序
1.数据元素类型定义

2.顺序表ST中查找值为key的数据元素(从最后一个元素开始比较)

改进:可以把待查关键字key存入表头(哨兵,监视岗)

特别需要注意for语句的“;”
3.算法分析
1.时间复杂度O(n)
查找成功时的平均查找长度,设表中各个记录查找概率相同
ASL=(n+1)/2
2.空间复杂度–一个辅助空间-----O(1)
4.提高查找概率

简单来说就是,把查找概率大的尽量放在后面查找次数少的
5.顺序查找优缺点
优点:算法简单,逻辑次序无要求,不同存储结构均适用
缺点:ASL太长,时间效率太低
2.折半查找(二分或对分查找)
每次将待查找记录所在区间缩小一半
1.折半查找算法(非递归算法)


2.折半查找(递归算法)
int Search_Bin(SSTable ST,KeyType key,int low,int high)
{
if(low>high)
return 0;
mid=(low+high)/2;
if(key==ST.elem[mid].key)
return mid;
else if(key<ST.elem[mid].key)
Search_Bin(ST,key,low,mid-1);
else if(key>ST.elem[mid].key)
Search_Bin(ST,key,mid+1,high);
}
3.算法分析
折半查找性能分析(判定树)
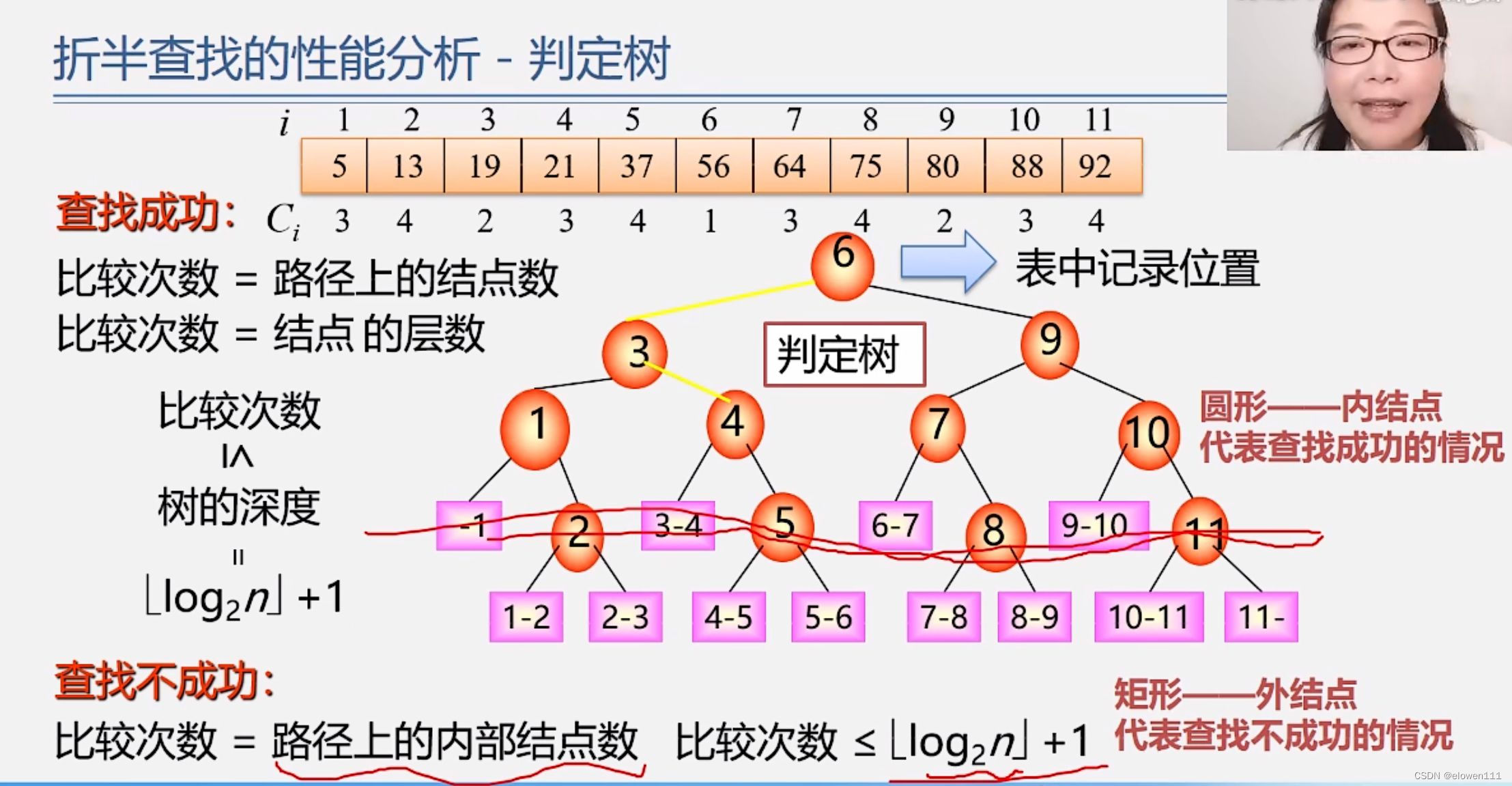

4.折半查找优缺点
优点:效率比顺序查找高
缺点:只适用于有序表,且限于顺序结构(对线性链表无效)
3.分块查找(索引顺序查找)
1.条件:
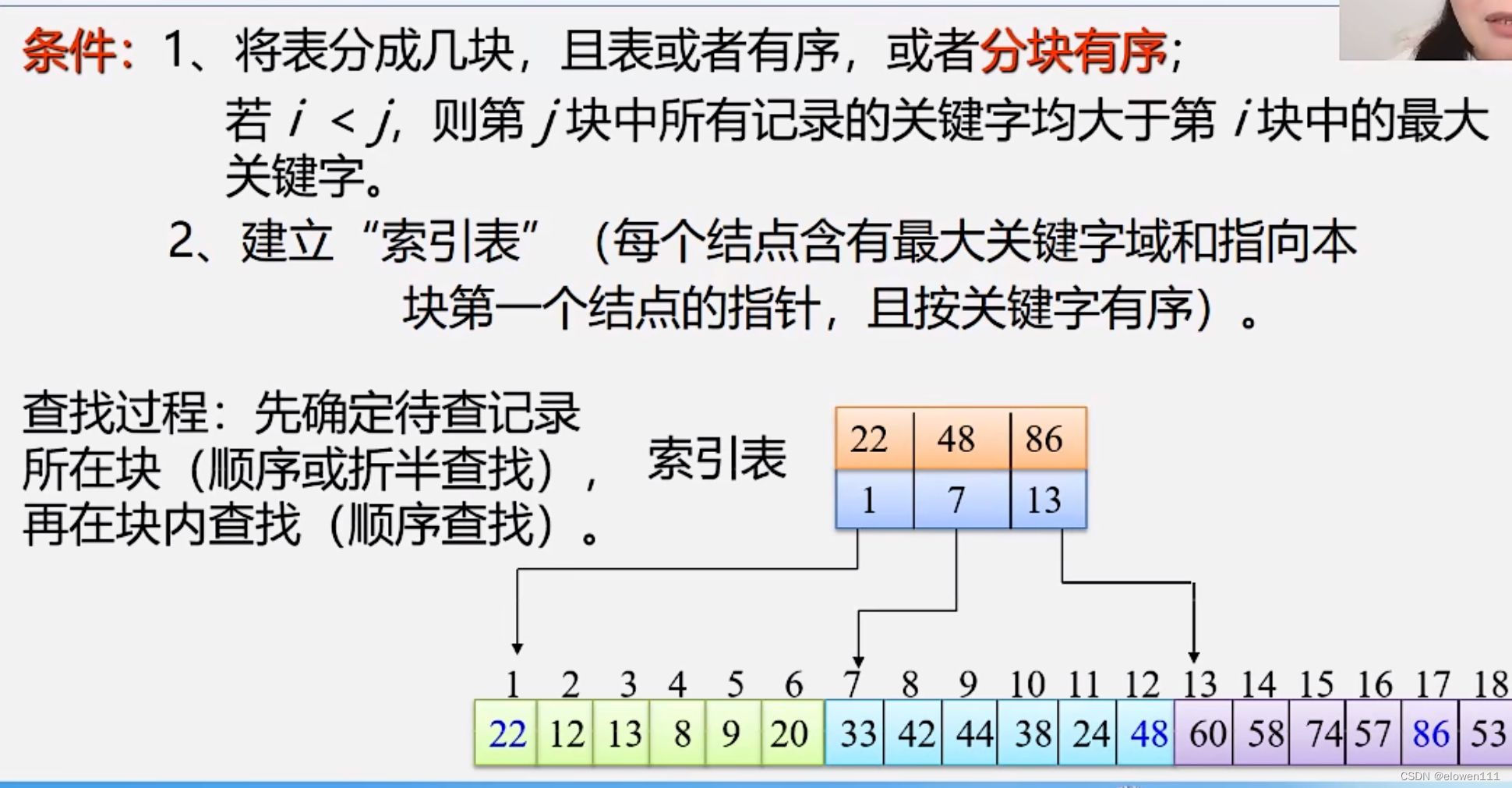
2.算法分析

3.优缺点

4.查找方法比较
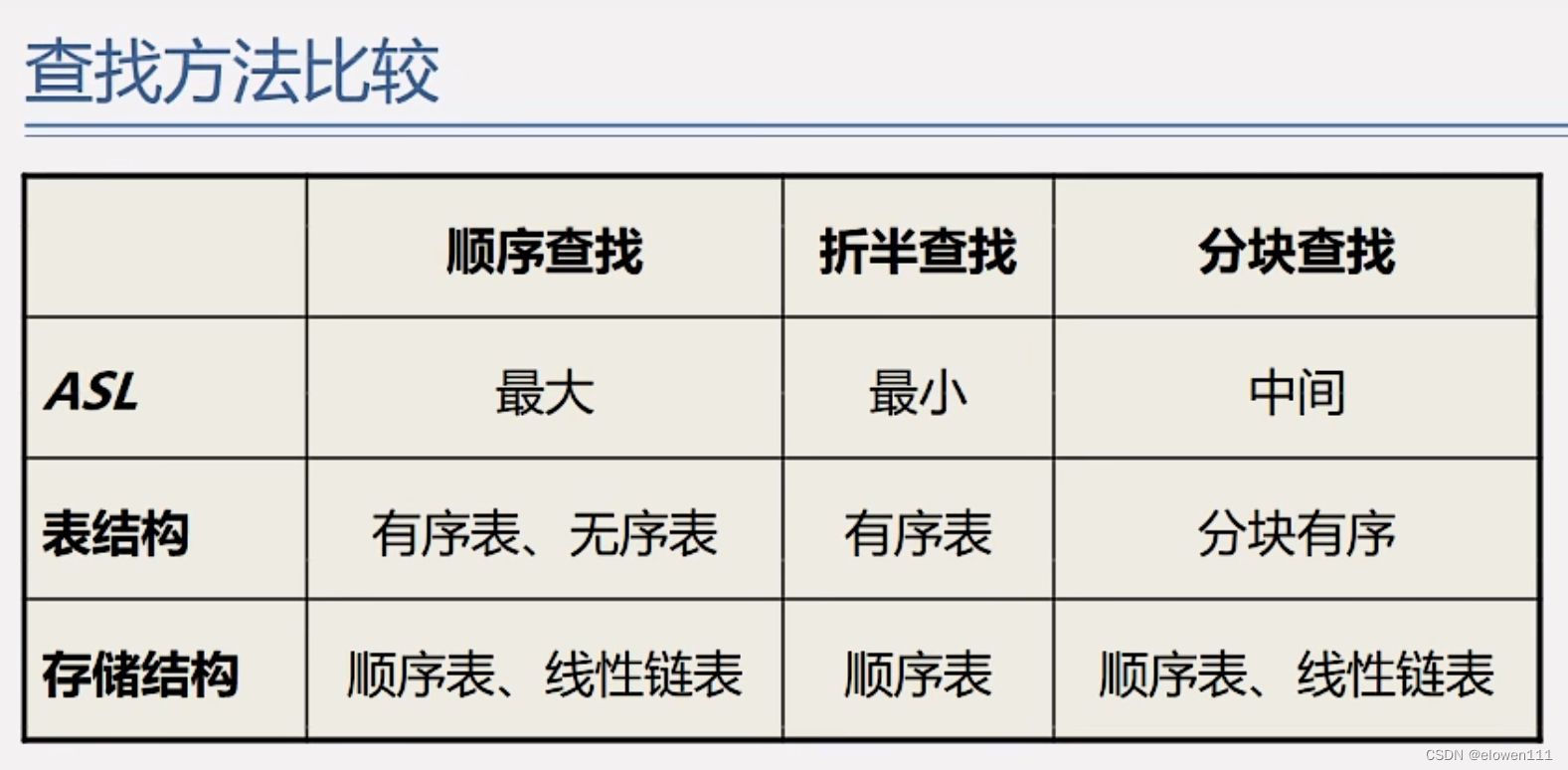
三.树表的查找

1.二叉排序树

性质:
中序遍历非空二叉排序树所得到的数据元素序列是一个按照关键字排序的递增有序序列
1.存储结构

2.算法思想

3.二叉排序树的递归查找
BSTree* SearchBST(BSTree *T,KeyType key)
{
if((!T)||key==T->data.key)
return T;
else if(key<T->data.key)
return SearchBST(T->ichild,key);
else if(key>T->data.key)
return SearchBST(T->rchild,key);
}
4.算法分析
二叉树上面查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径
比较的关键字次数=此结点所在的层次数
最多的比较次数=树的深度
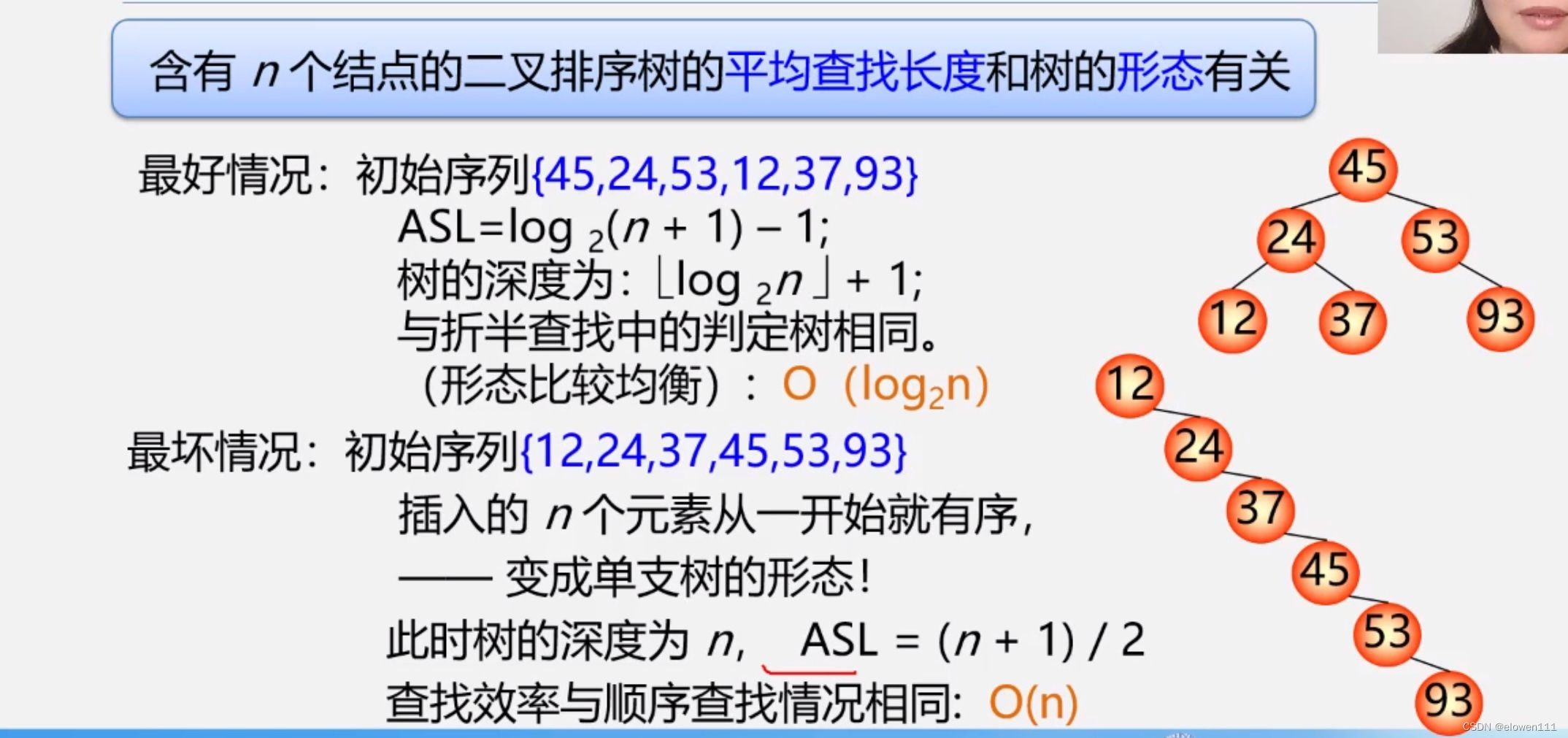
5.提高形态不平衡的二叉排序树的查找效率–平衡二叉树
6.二叉排序树的操作
1.插入

2.生成
从空树出发,经过一系列查找,插入操作之后,可以生成一颗二叉排序树

3.删除
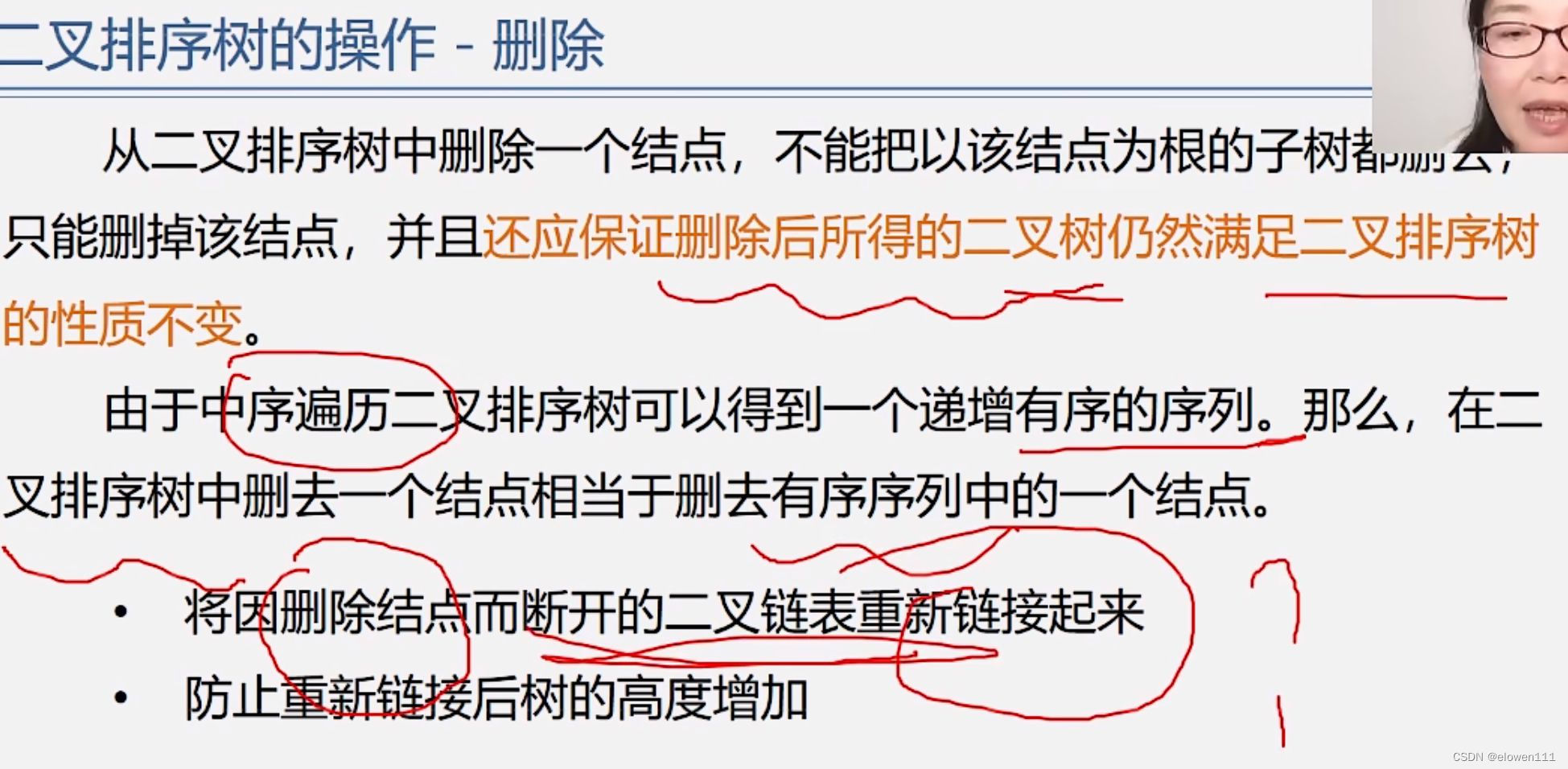
1.删除的是叶子结点
直接删除该结点

2.被删除的结点只有左子树或者只有右子树
直接用其左子树或者右子树替换

3.被删除的结点既有左子树又有右子树

2.平衡二叉树
1.定义

2.失衡二叉树的分析和调整
平衡调整的四种类型
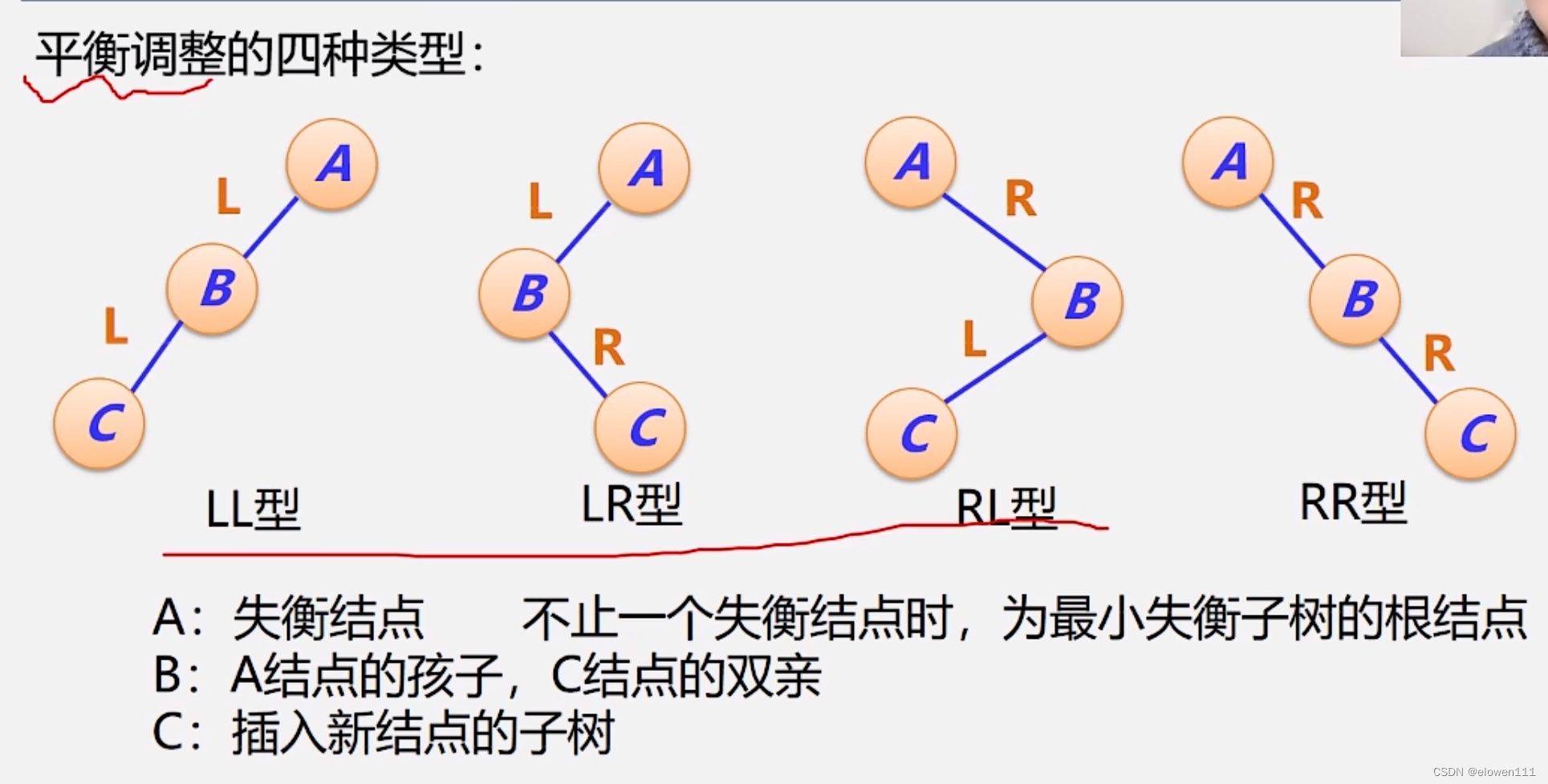
调整原则:
1.降低高度
2.保持二叉排序树的性质
3.散列表的查找
1.基本概念
记录存储位置与关键字之间存在的对应关系
对应关系—hash函数
2.散列表的术语


3.散列函数构造方法

1.直接定址法
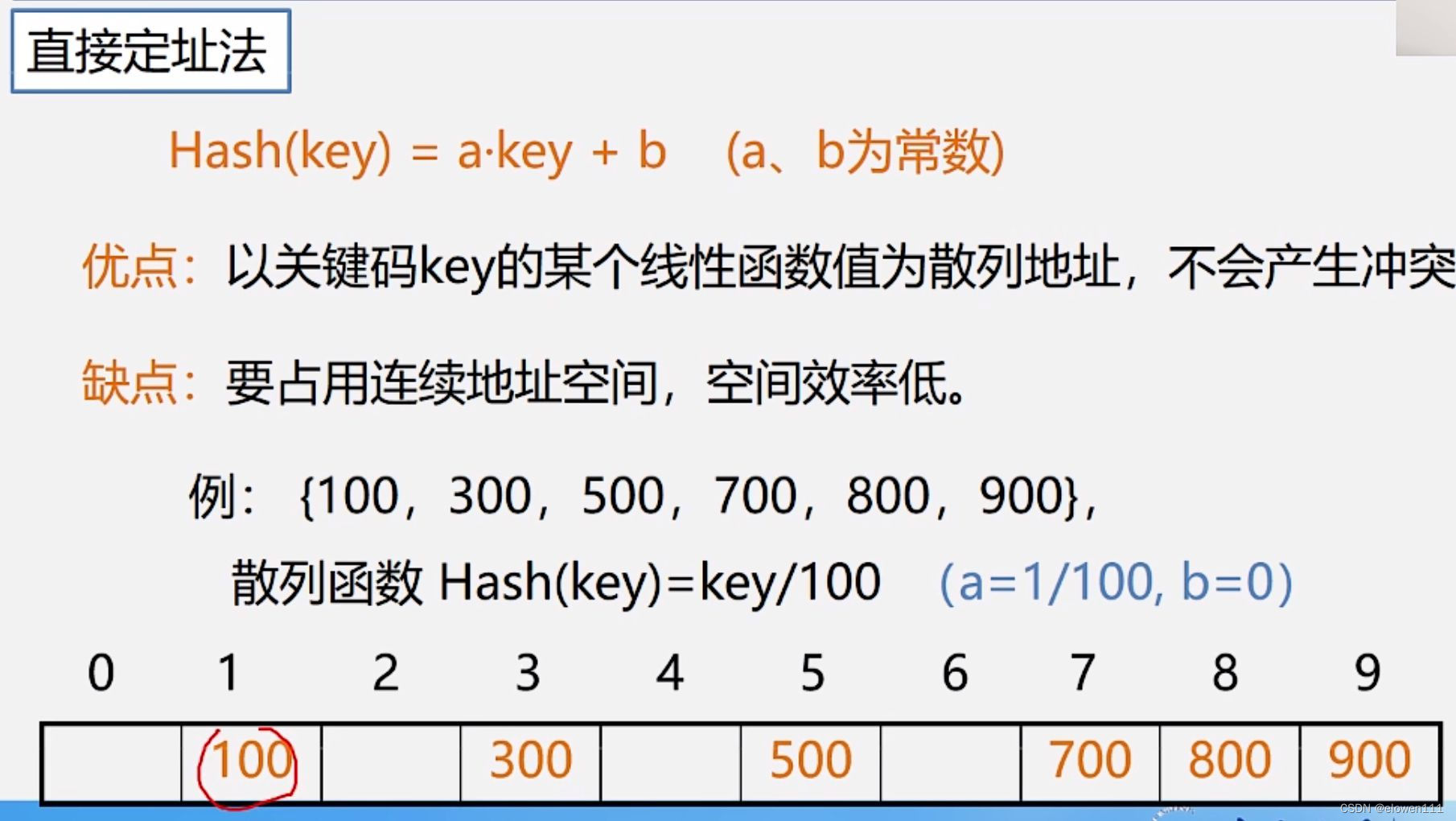
2.除留余数法

4.处理冲突的方法
1.开放地址法



2.链地址法(拉链法)
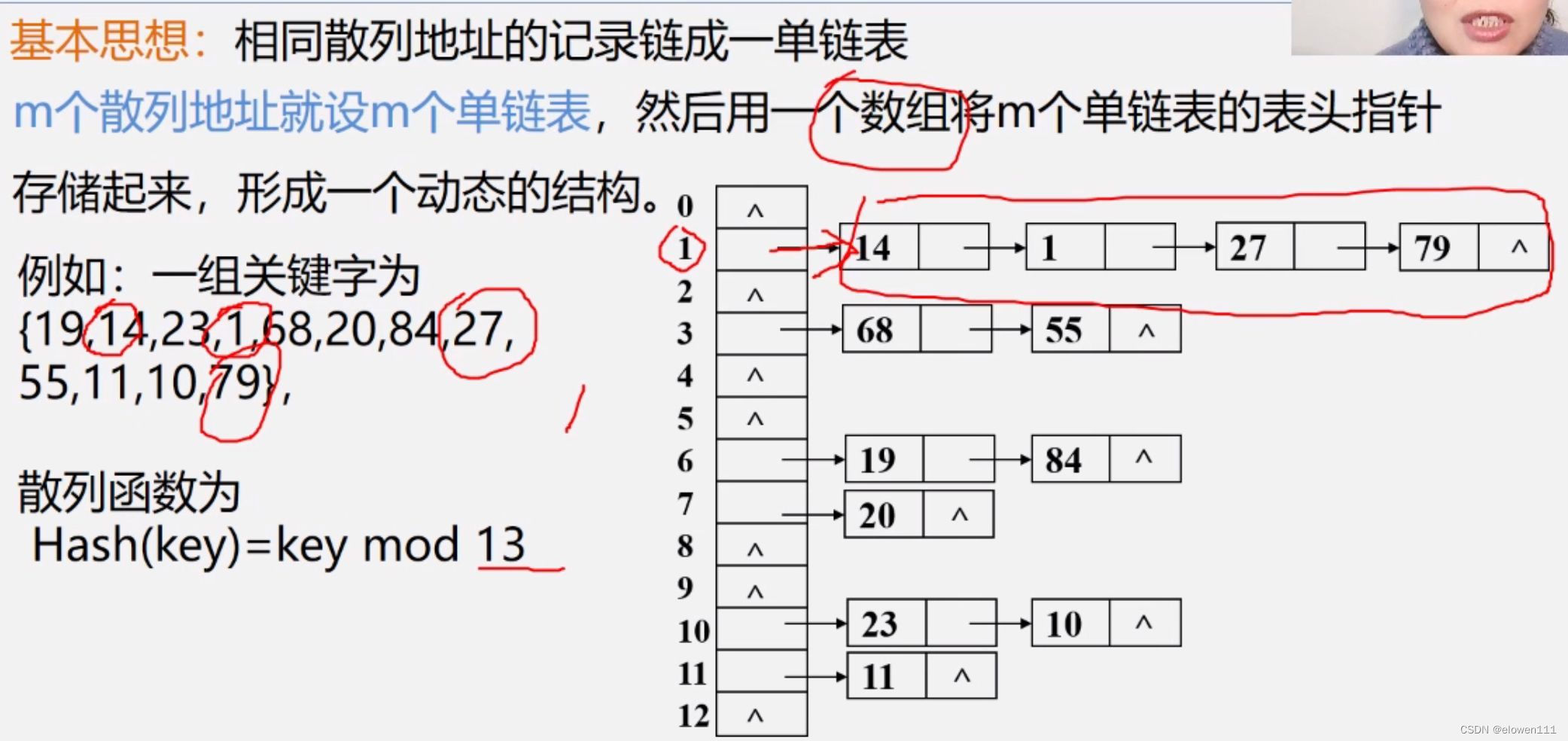

5.散列表的查找
查找过程



- 散列表技术具有很好的平均性能,优于一些从传统技术
- 链地址法优于开地址法
- 除留余数法作散列函数优于其他类型的函数
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








