递归：概念、应用与实例解析-优快云博客

这篇文章我们将介绍一种解决问题的方法：递归

递归的概念

递归指函数自己调用自己，如下图就是个简单递归的实现：

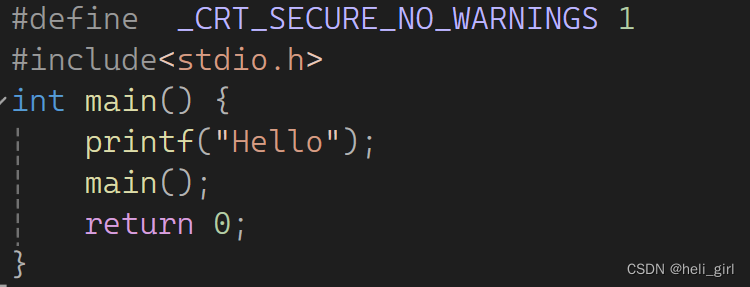
这里在main函数中调用了main函数，我们可以预测这个程序将会不停的打印“Hello”，因为每一次main函数的调用都会在栈帧中占用一篇内存空间，因为计算机的存储空间有限，所以如果程序不停的调用main函数最后会造成栈溢出，如图：

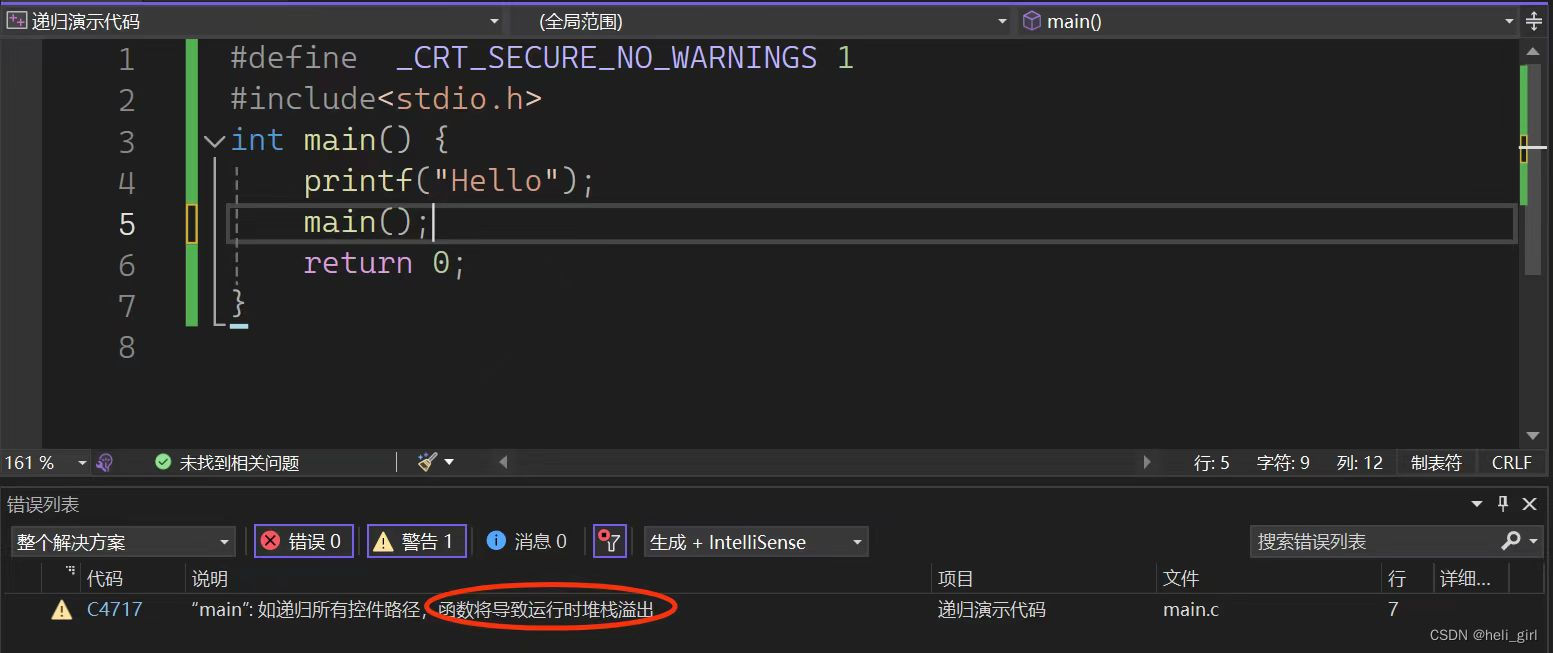
所以为了避免栈溢出，我们给函数调用加上一个限制条件，同时，限制条件有以下两个要求：

满足条件不再递归
每次函数递归后越来越接近这个条件

比如，将以上代码修改，给main函数加上一个计数器count，用来计数，每次递归后减一，当count=0时函数不再递归，代码实现如下：

这样我们就避免程序出现栈溢出的情况。

递归的思想

大事化小：把大型复杂问题转化成一个与原问题相似但规模小的子问题

在这我们可以类比于高中所学的数列问题，如：

我们可以通过两种方法求出第n项

通过数列的通项公式去求解第n项
知道第m和n项之间的关系，通过第m项去求解第n项

递归就是用到第二种方法，只要知道两项之间的关系，不断向前递推，直到推到第1项，然后，从第一项一步步回归求出第n项，所以递归这个词包含两种意思：

递：递推，展开函数
归：回归，从极致一步步回推（极致如数列中的第一项，不可再向前展开了）

递归的好处

使用简单的代码就可以完成复杂的任务，接下来我将通过实例，为读者讲解

递归的应用

示例：斐波那契数列

斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368

特别指出：第0项是0，第1项是第一个1。

这个数列从第3项开始，每一项都等于前两项之和，所以我们可以写出它的递推公式来：

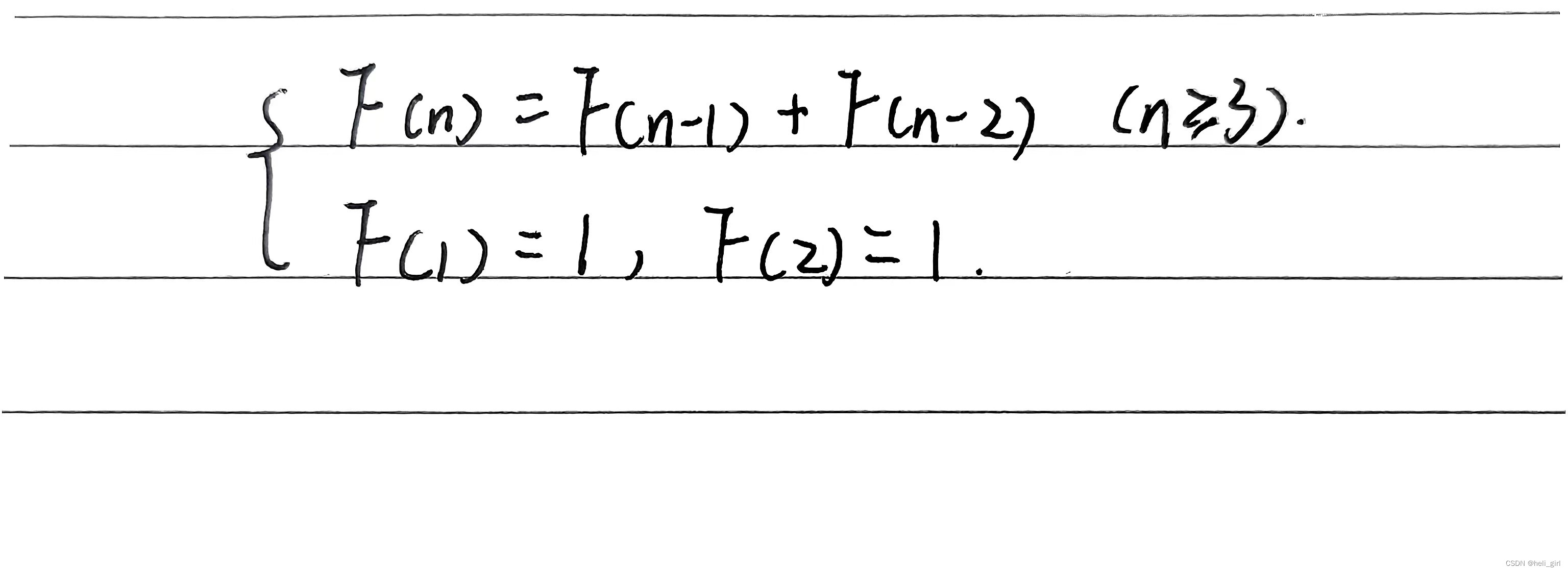
将其转换为编程语言，代码如下：

#include<stdio.h>
int func(int n) {
	if (n > 2) {
		return func(n - 1) + func(n - 2);
	}
	else
	return 1;
}
int main() {
	int n,f;
	scanf("%d", &n);
	f = func(n);
	printf("%d", f);
	return 0;
}

但此数列的通项公式为：

如果用通项公式表达起来非常复杂，所以将复杂问题转化成递推问题往往可以使代码更简单，同时更易于人理解

实战一：青蛙跳台阶问题

青蛙跳台阶讲的是有只青蛙，一次可以跳1或2节台阶，问青蛙跳到n阶台阶时共有几种跳法？

首先我们可以将这个问题分阶段来看，当台阶是2的时候青蛙有两种选择，第一种是第一步选择跳一阶，第二种是第一步选择跳两阶，对于两级来说只有两种选择，如图：

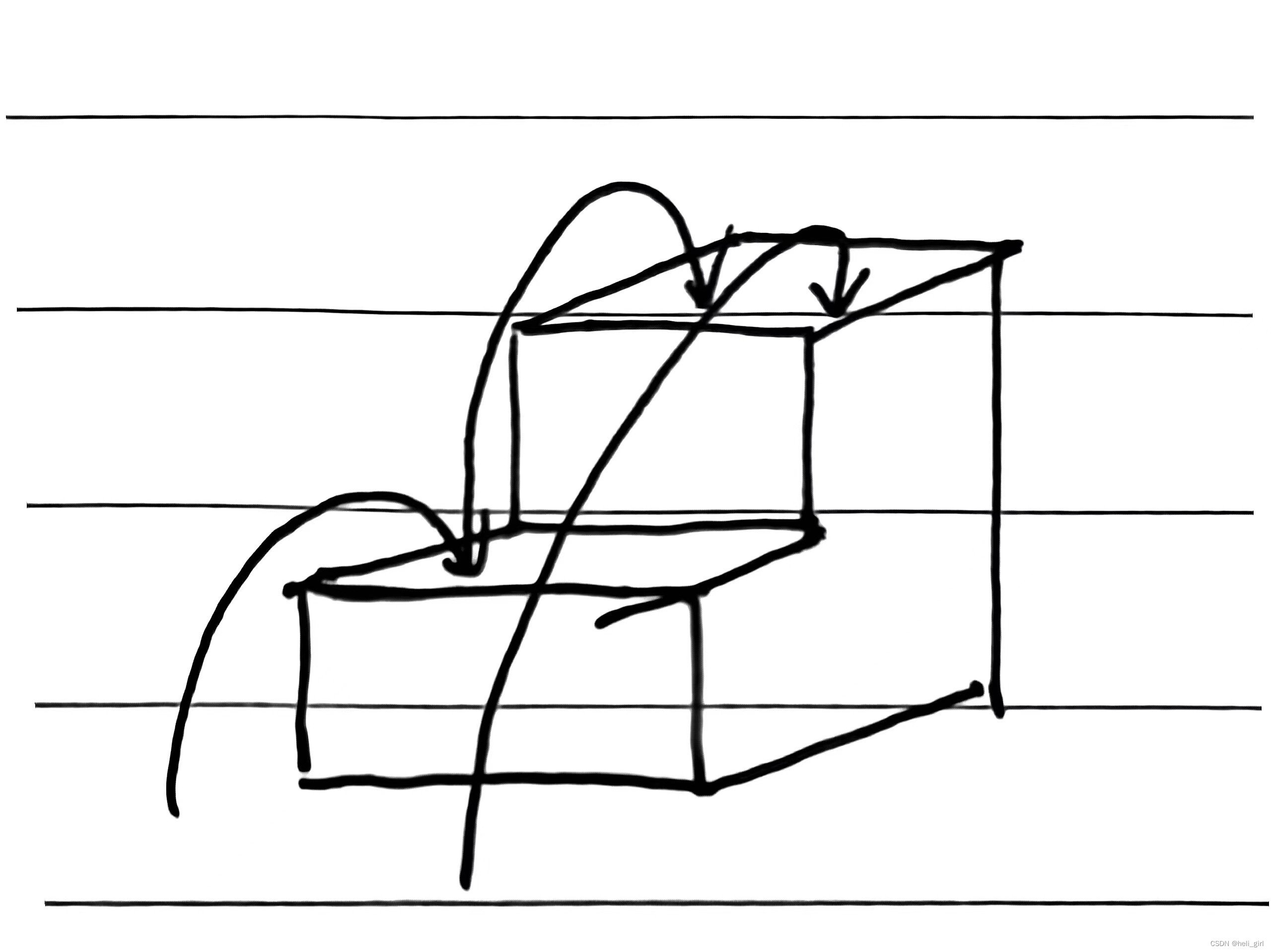
当台阶是三时有三种选择，如图：

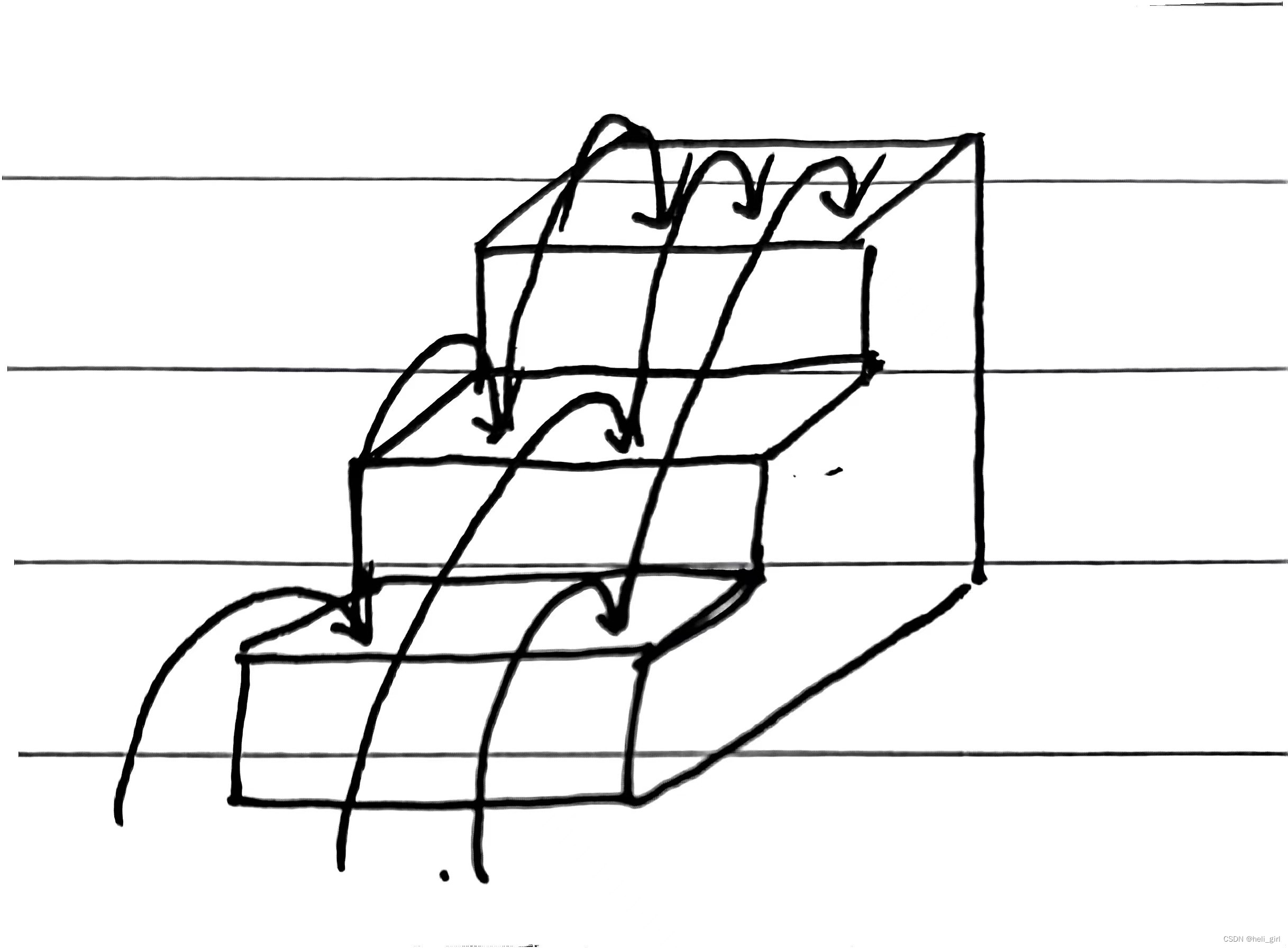
经过观察我们可以将跳台阶的过程分为两个部分，第一步选择和第一步之后的所有选择，如图：

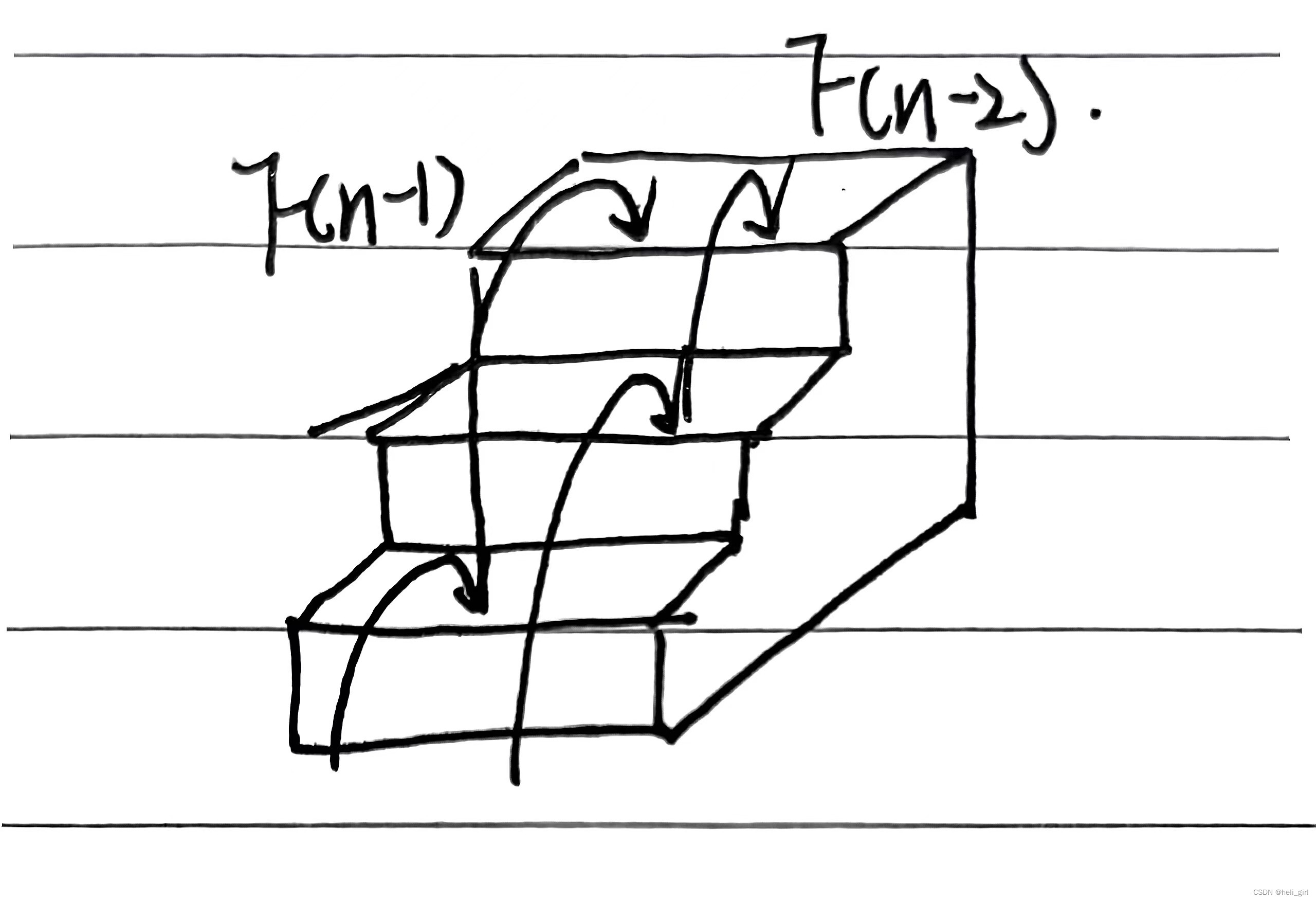
当第一步选择是跳一阶时，剩下n-1阶需要选择，当第一步选择跳二阶时剩下n-2阶需要选择，而总选择为F(n-1)+F(n-2)，所以我们可以列出一个递归函数如下：

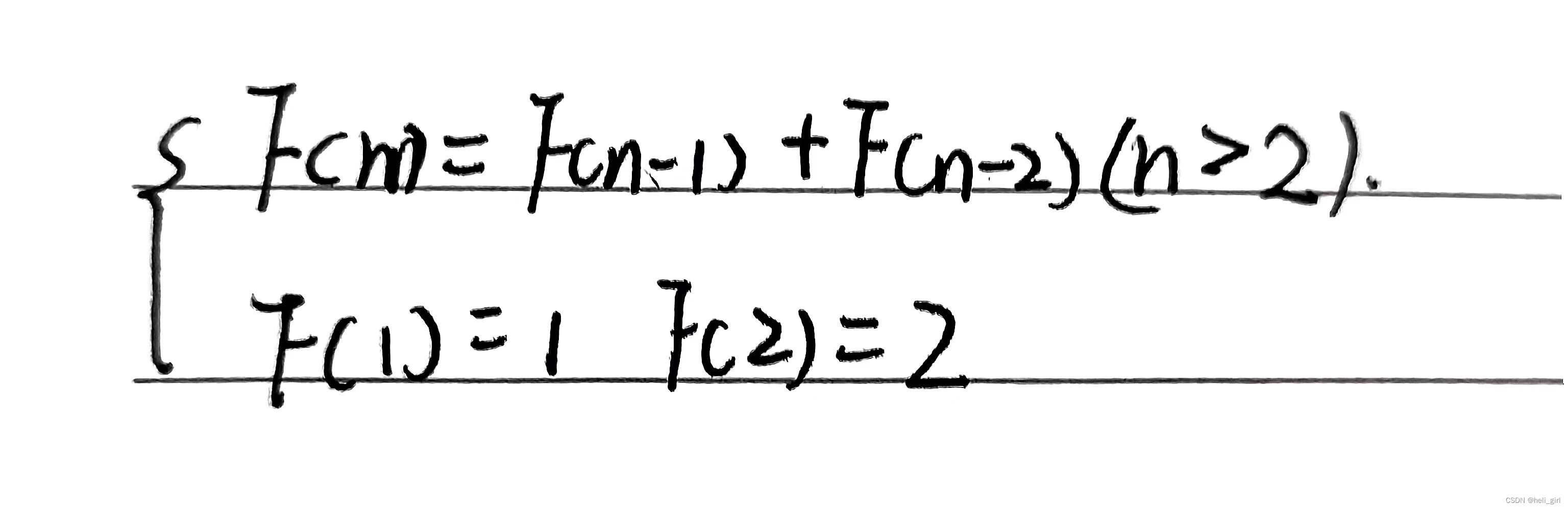
将其转化成编程语言如下：

#include<stdio.h>
int step(int n) {
	int count = 0;
	if (n > 2) {
		count = step(n - 1) + step(n - 2);
	}
	else if (n == 1)count = 1;
	else if (n == 2)count = 2;
	return count;
}
int main() {
	int n, s;
	scanf("%d", &n);
	s = step(n);
	printf("%d", s);
	return 0;
}

实战二：汉诺塔问题

有三根杆子A,B,C。A杆上有若干碟子
每次移动一块碟子,小的只能叠在大的上面
把所有碟子从A杆全部移到C杆上

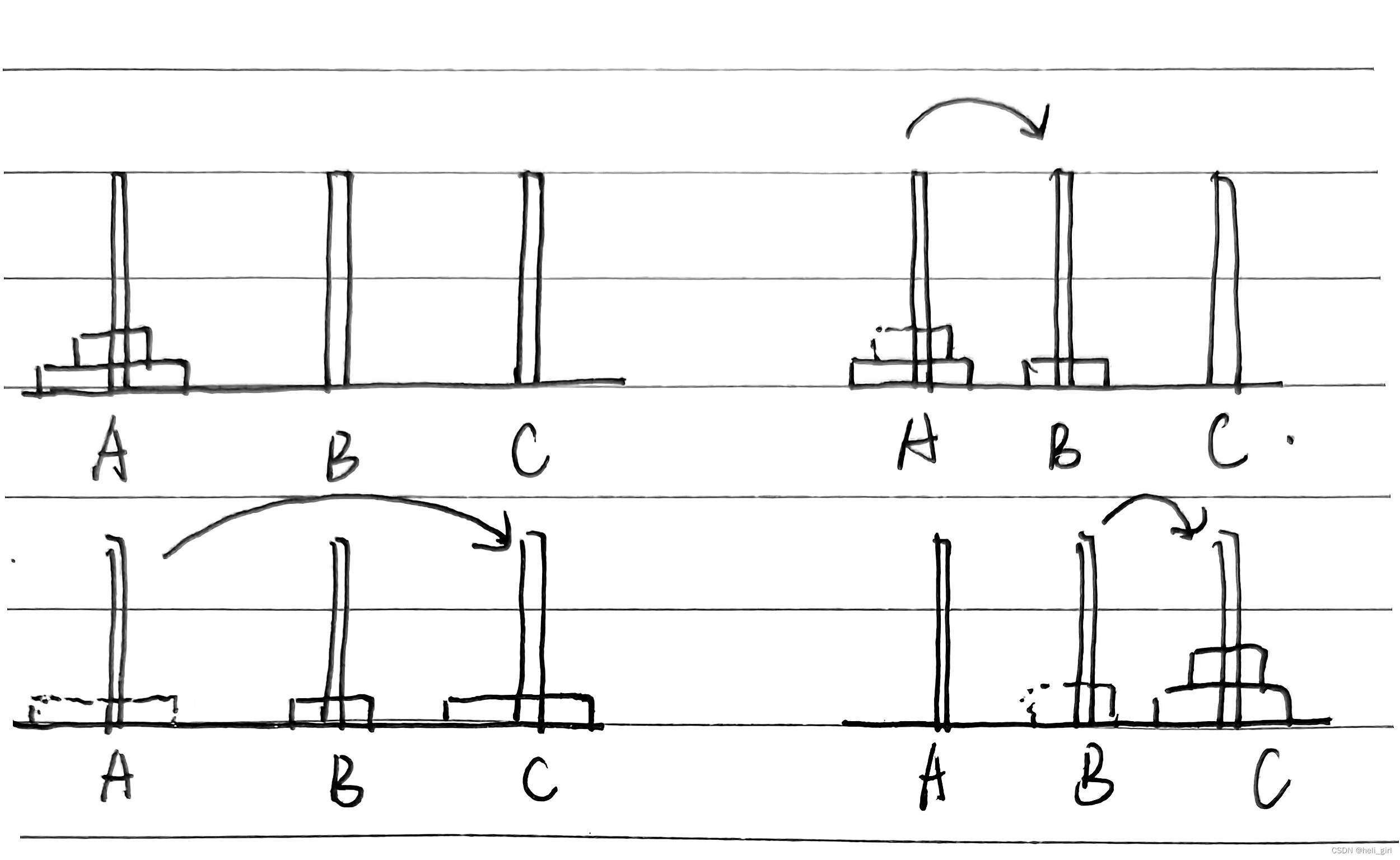
问将所有碟子从A杆移动到C杆需要多少步，将其用动态图来表示为：

我们需要把A柱的盘子，移动到C柱同时需要保证小的盘子只能在大的上面，让我们把这个问题简化成只有两个盘子，这时我们需要把最上面的盘子从A移动到B，再把底下的盘子从A移动到C，再把盘子从B移动到C，总共需要三步，如图：

当盘子更多时，我们可以把n-1个盘子看成整体，这时候只有最底下的盘子和剩下的n-1个盘子，我们可以将其类比于两个盘子，动态如图：

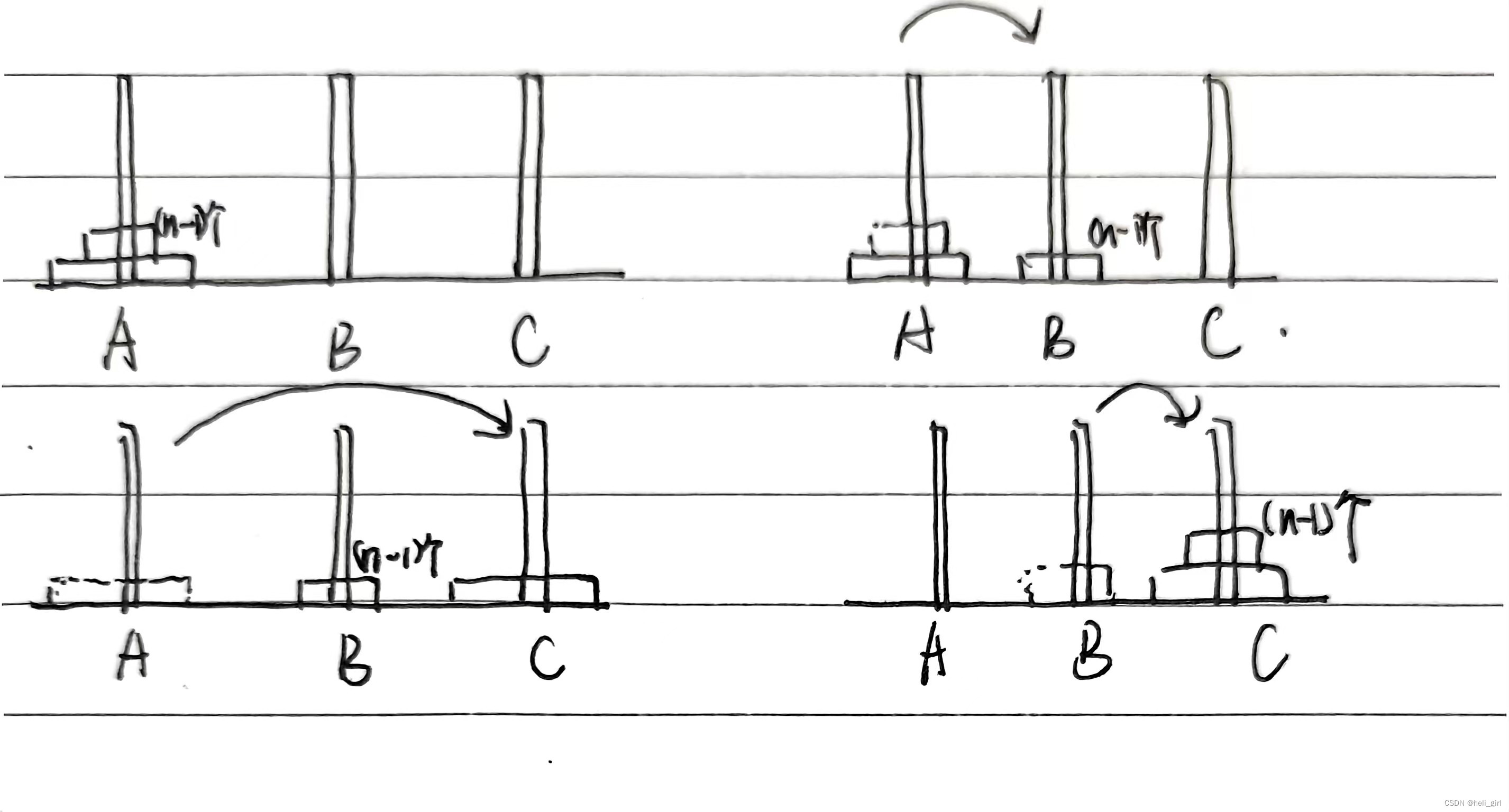
同时，n-1又可以看成第n-1个盘子和剩下n-2个盘子，这样我们就可以得到一个递归关系：

首先，将n-1个盘子从A移动到B
再将最底下的盘子从A移动到C
最后将n-1个盘子从B移动到C

这样我们就得到了一个递归关系，将其转化为编程语言如下：

#include<stdio.h>
int count = 0;
void move(int n, char a, char b, char c) {
	if (n == 1) {//将最低下的盘子从A移到C
		count++;
		printf("step %d\n", count);
		printf("%c->%c\n", a, c);
	}
	else {
		move(n - 1, a, c, b);//将n-1个盘子从A移到B
		count++;
		printf("step%d\n", count);
		printf("%c->%c\n", a, c);
		move(n - 1, b, a, c);//将n-1个盘子从B移动C
	}
}
int main() {
	int n, s;
	char A, B, C;
	A = 'A';
	B = 'B';
	C = 'C';
	scanf("%d", &n);
	move(n,A,B,C);
	printf("sum = %d\n", count);
	return 0;
}