快速排序

目录

快速排序

基本思想

快速排序实现主框架

 _QuickSort方法

 hoare版本

代码实现

问题一：为什么跳出循环后 right 位置的值一定不大于key?

问题二：为什么left和right指定的数据和key值相等时也要交换？

 挖坑法

  动图实现  ​编辑

代码实现 

 lomuto前后指针

 算法思路

 动图实现

代码实现

 快速排序特性总结

 非递归版本

代码实现 

---

快速排序 

 

基本思想

快速排序是Hoare于1962年提出的⼀种⼆叉树结构的交换排序方法，

其基本思想为：任取待排序元素 序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

 

举例 

例如有数据集合 ： 9  2  13  23  7  8  10

选取 9 为基准值，则第一遍排序后 ： ( 8  2 7 )  9  ( 23  13  10)  

此时左子序列(即 9 左括号里) 的元素都比 9 小，右子序列的元素都比 9 大。(此时 9 的位置已经定了)

然后再不断对左子序列与右子序列进行此操作。不断排序后将会得到整体有序序列。

 

快速排序实现主框架

void QuickSort(int* a, int left, int right)
{
	if (left >= right)  
	{
		return;
	}
	int meet = _QuickSort(a, left, right);  // 
	QuickSort(a, left, meet -1);
	QuickSort(a, meet + 1, right);
}

 

 _QuickSort方法

将区间中的元素进行划分的 _QuickSort 方法主要有以下几种实现方式：

 

 hoare版本

算法思路：

• 创建左右指针，确定基准值
• 从右往左找出比基准值小的数据，从左往右找出比基准值大的数据，左右指针交换，进入下次循环

 

代码实现

int _QuickSort(int* a, int left, int right) 
{
     int begin = left;
     int end = right;
     int keyi = left;
     ++left;
     while (left <= right)
     {
         // 右边找⼩ 
         while (left <= right && a[right] > a[keyi])
         {
             --right;
         }
         // 右边找⼩ 
         while (left <= right && a[left] < a[keyi])
         {
             ++left;
         }
         if (left <= right)
         {
             swap(&a[left++], &a[right--]);
         }
     }
     swap(&a[keyi], &a[right]);
     return right;
}

 

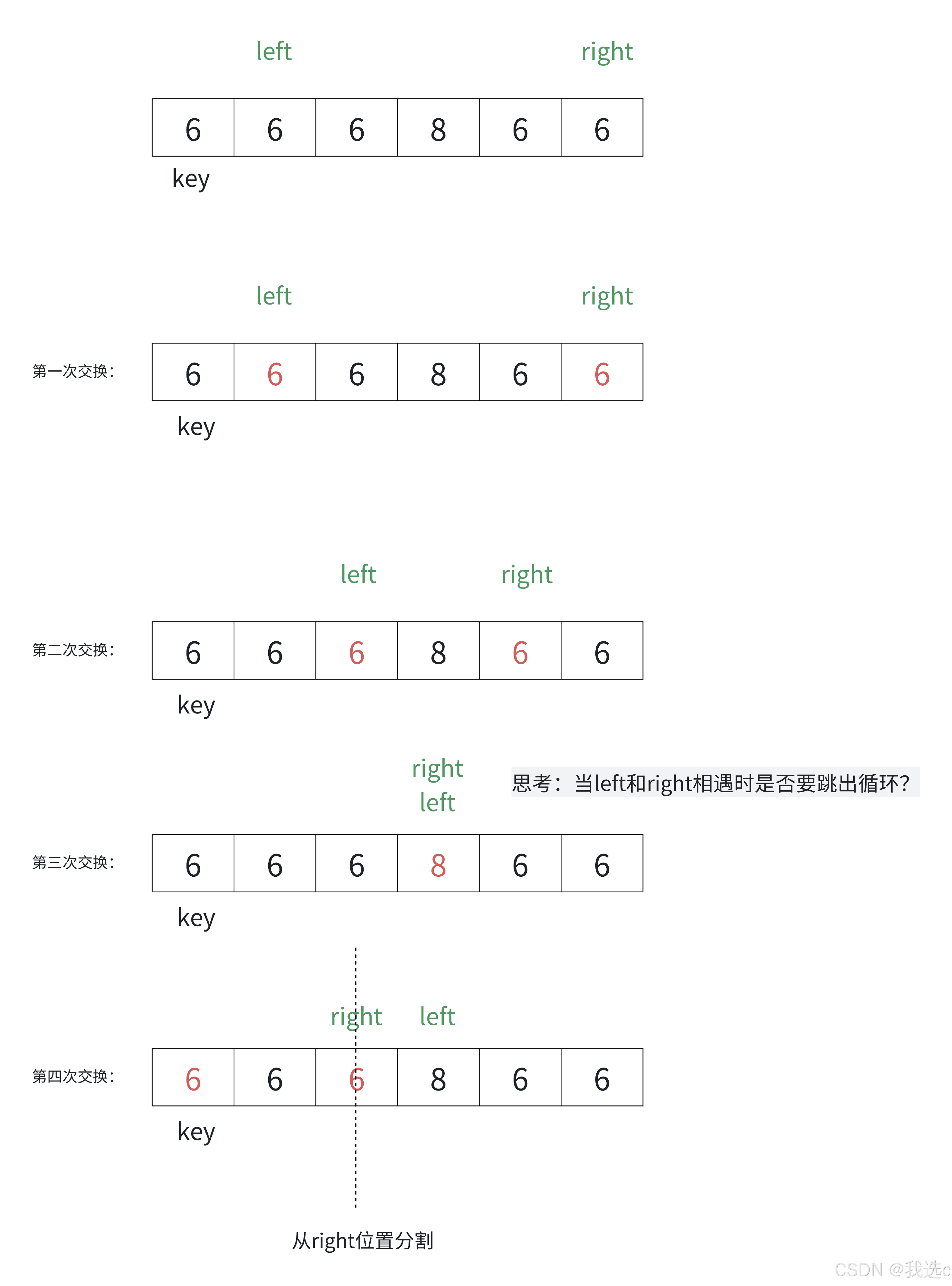
问题一：为什么跳出循环后 right 位置的值一定不大于key?

当 left > right 时，即是 right 走到 left 的左侧，而 left 扫描过的数据均不大于key，因此 right 此时指向的数据一定不大于 key

 

问题二：为什么left和right指定的数据和key值相等时也要交换？

相等的值参与交换确实有⼀些额外消耗。实际还有各种复杂的场景，假设数组中的数据大量重复时， 无法进行有效的分割排序

 

 

 挖坑法

思路： 创建左右指针。首先从右向左找出比基准小的数据，找到后立即放入左边坑中，当前位置变为新 的"坑"，然后从左向右找出比基准大的数据，找到后立即放入右边坑中，当前位置变为新的"坑"，结 束循环后将最开始存储的分界值放入当前的"坑"中，返回当前"坑"下标（即分界值下标）

 
 动图实现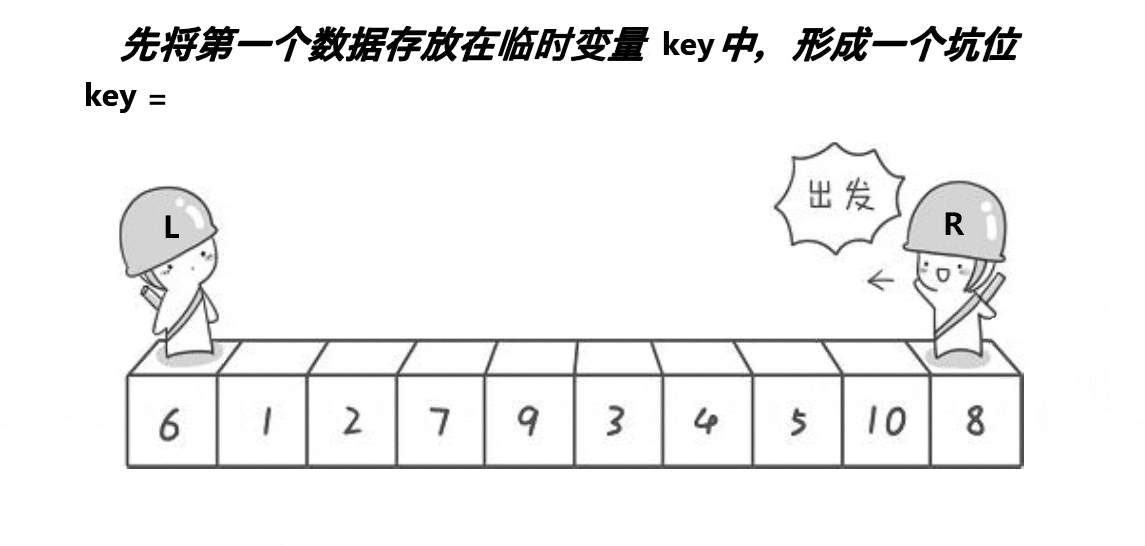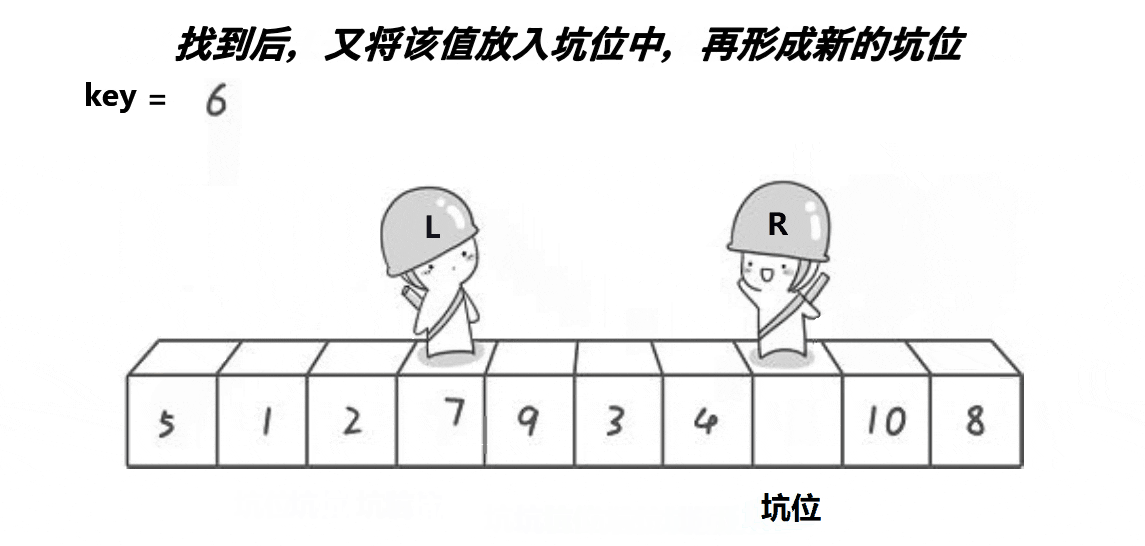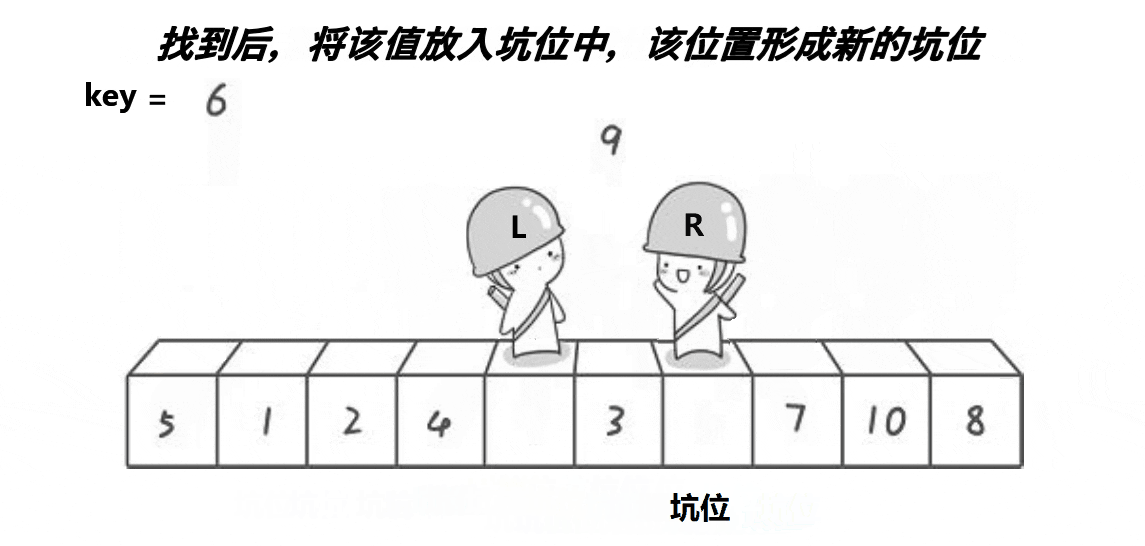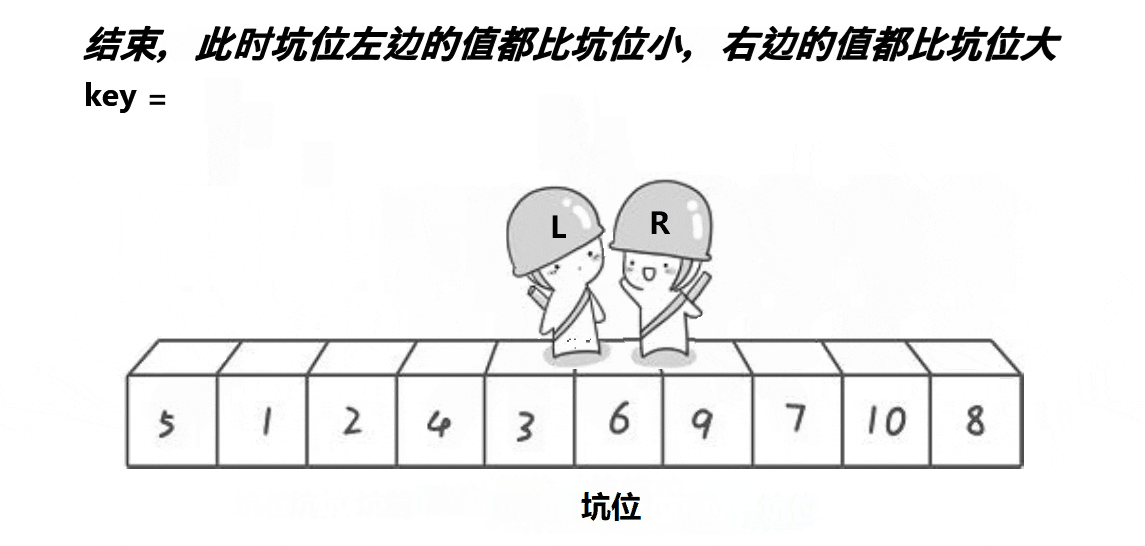  

代码实现 

int _QuickSort(int* a, int left, int right) 
{
     int mid = a[left];
     int hole = left;
     int key = a[hole];
     while (left < right)
     {
         while (left < right && a[right] >= key) 
         {
             --right;
         }
         a[hole] = a[right];
         hole = right;
         while (left < right && a[left] <= key)
         {
             ++left;
         }
         a[hole] = a[left];
         hole = left;
     }
     a[hole] = key;
     return hole;
}

 

 lomuto前后指针

 

 算法思路

创建前后指针，从左往右找比基准值小的进行交换，使得小的都排在基准值的左边。

 动图实现

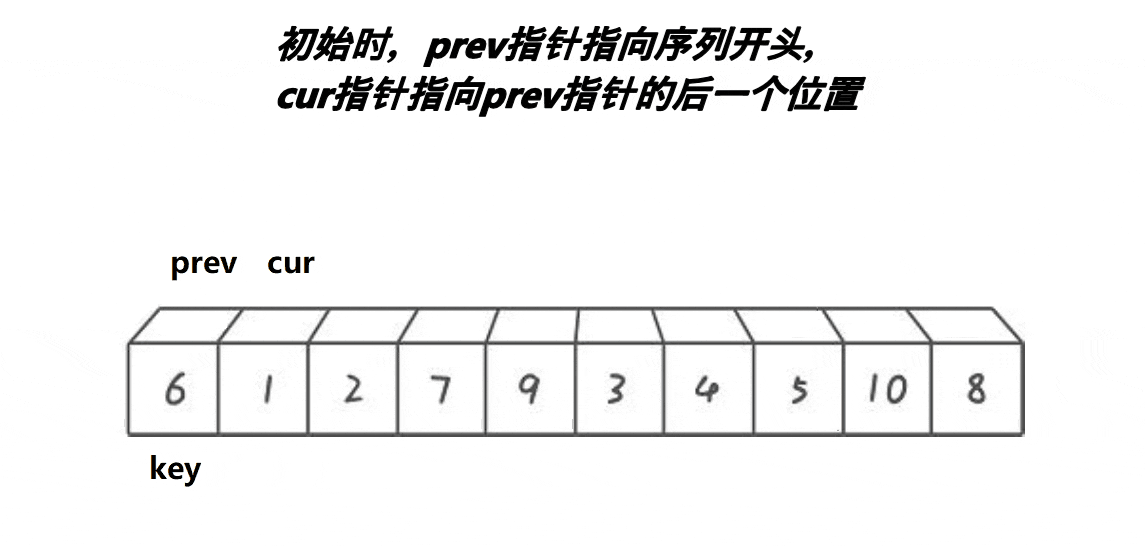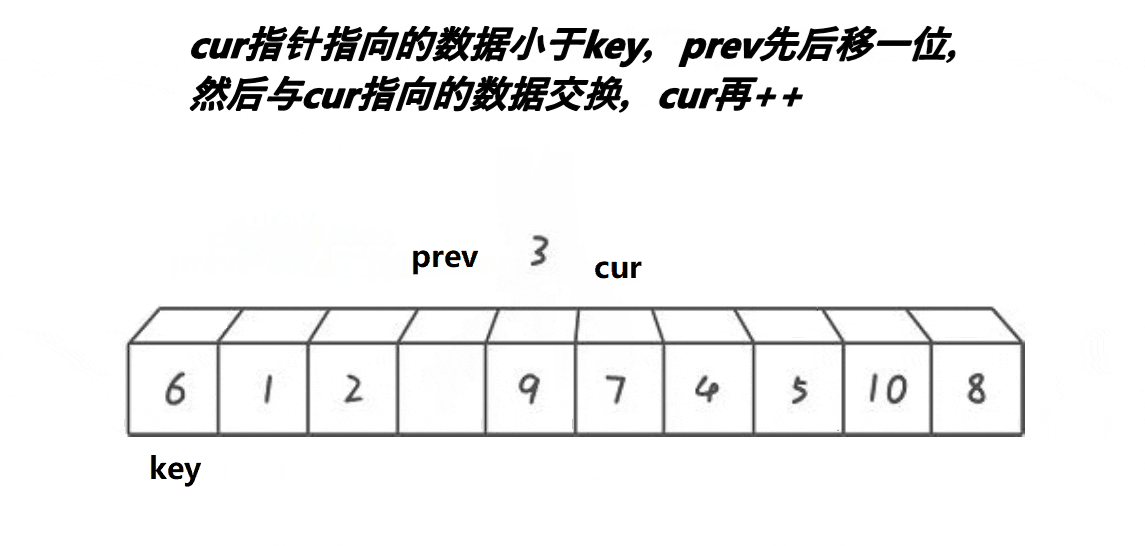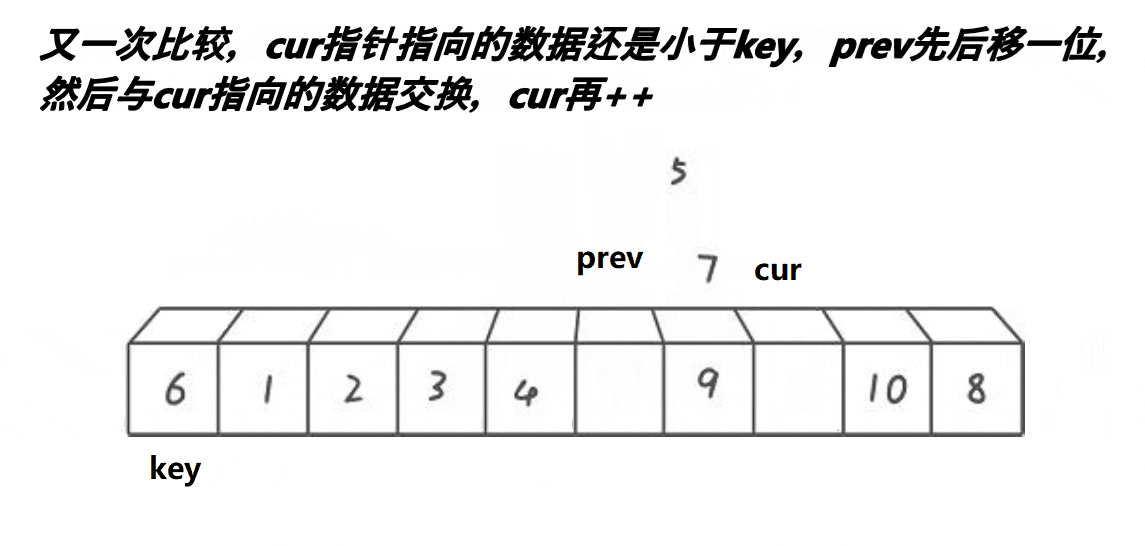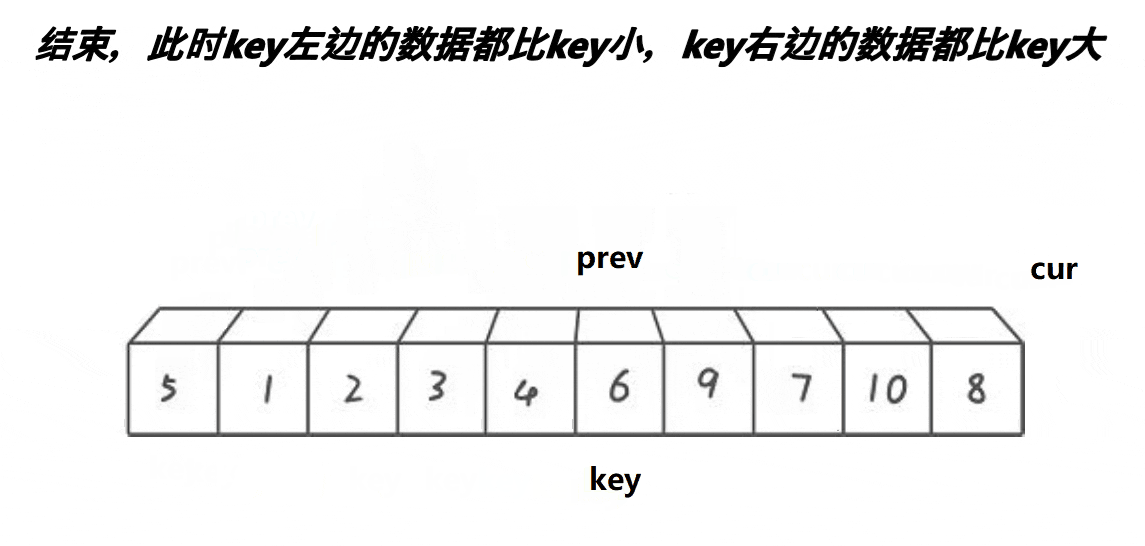
代码实现

 

int _QuickSort(int* a, int left, int right) 
{
     int prev = left, cur = left + 1;
     int key = left;
     while (cur <= right)
     {
         if (a[cur] < a[key] && ++prev != cur) 
         {
             swap(&a[cur], &a[prev]);
         }
         ++cur;
     }
     swap(&a[key], &a[prev]);
     return prev;
}

 

 快速排序特性总结

• 1. 时间复杂度：O(nlogn)
• 2. 空间复杂度：O(logn)

 

 非递归版本

非递归版本的快速排序需要借助数据结构：栈 

代码实现 

void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);
	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);
		// 单趟 
		int keyi = begin;
		int prev = begin;
		int cur = begin + 1;
		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ++prev != cur)
				Swap(&a[prev], &a[cur]);
			++cur;
		}
		Swap(&a[keyi], &a[prev]);
		keyi = prev;
		// [begin, keyi-1] keyi [keyi+1, end] 
		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}
	STDestroy(&st);
}