双 指 针

   双指针技巧是解题时的常用技巧，其大体分为同向双指针、快慢指针、对向双指针。通常我们把

窗口长度固定的题目叫做滑动窗口，长度不固定时叫做双指针类题目。

   关于双指针类的题目，一部分只是将代码以双指针的形式表达出来的，并没用单调性(贪心)方面

的考虑，这类题目相对较简单；但当题目涉及单调性时，这类用双指针的题目较难。

   下面以题目来体会用双指针解题：

奇偶排序

class Solution {
public:
    void swap(vector<int>& nums, int i, int j) {
        int rem = nums[i];
        nums[i] = nums[j];
        nums[j] = rem;
    }
    vector<int> sortArrayByParityII(vector<int>& nums) {
        int pos = nums.size() - 1;
        int odd = 1, even = 0;
        for (; odd < nums.size() && even < nums.size();) {
            if (nums[pos]&1) {
                swap(nums, pos, odd);
                odd += 2;
            }

            else {
                swap(nums, even, pos);
                even += 2;
            }
        }
        return nums;
    }
};

  此题就不涉及单调性的问题；在数组的左边界设置两个指针，用来标记奇数位置和偶数位置；在数组的右边界设置一个数据指针，用来传递数据

 寻找重复的数

class Solution {
public:
    int findDuplicate(vector<int>& nums) {
        int slow = nums[0];
        int fast = nums[nums[0]];
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[nums[fast]];
        }
        fast = 0;
        while (fast != slow) {
            fast = nums[fast];
            slow = nums[slow];
        }
        return fast;
    }
};

  此题也不涉及单调性的问题；解决此题时，最直接的思路是用一个哈希表记录遍历过的数字，但这不符合题目对空间的要求。

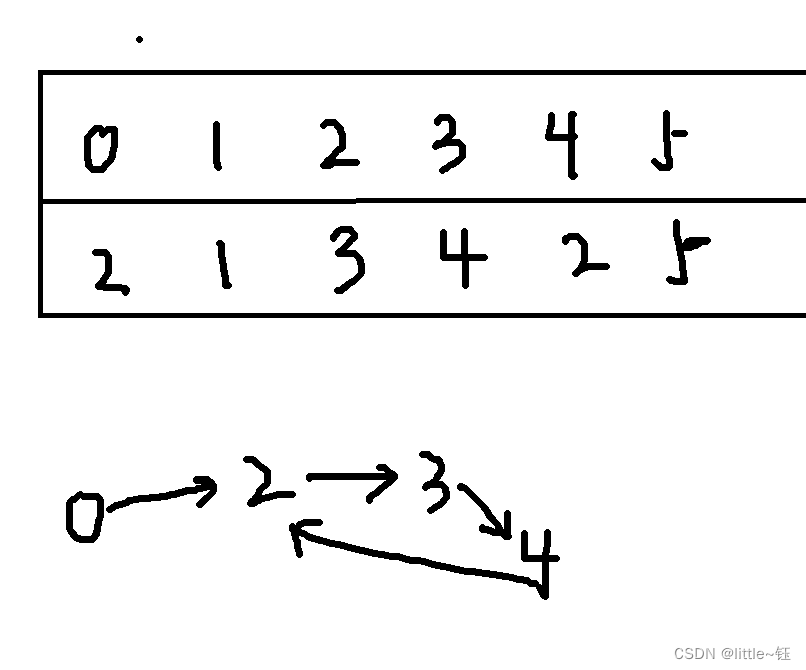
  有n+1个数，范围在1-n以内，我们从下标0对应的数开始，以每个数组中每个数作为下标去索引到下一个位置，画出如上图的线路图，如果有重复的数字，最后一定会形成一个回路，这转化为找环形链表的入口。

  接雨水

class Solution {
public:
    int trap(vector<int>& height) {
        int l = height[0], r = height[height.size() - 1];
        int ans = 0;
        int i = 1, j = height.size() - 2;
        while (i <= j) {
            if (l > r) {
                ans += max(0, r - height[j]);
                r = max(r, height[j]);
                j--;
            } else {
                ans += max(0, l - height[i]);
                l = max(l, height[i]);
                i++;
            }
        }
        return ans;
    }
};

   求整个区域接水的量，可以分别求每个柱体可以接的水的体积求和。对于求每个柱体可以接的水

的体积，只要知道其左右两边柱体的最大高度，用其最大高度中的最小值减去要求的柱体的高度就

是此柱体可以接的体积(注：当左右的最大高度都小于柱体的高度，就不能接水，coding时高度差

需要和0比较)。

    要求左右两边的最大高度，可以先预处理出两个数组分别记录从0~l和从r~size-1区间的最大高

度，然后只要遍历一遍数组统计体积就可以，这样时间复杂度达到最优，但空间复杂度并不是最

优。我们可以在数组的左右两边设置左右指针向中间遍历，并用两个变量了l,r记录左右指针划过的

区域中的最大高度，当l大于r时，对于右指针所指向的柱体，虽然不知道其左边区域的最大值是多

少(因为l只记录了左指针左边区域的最大值)，但一定不会小于l，此时r减去柱体的高度就是右指针

指向柱体所能接的水的体积；当了l<r时同理。这样就用有限的变量就可以完成统计

救生艇

class Solution {
public:
    int numRescueBoats(vector<int>& people, int limit) {
        sort(people.begin(), people.end());
        int l = 0, r = people.size() - 1;
        int ans = 0;
        while (l <= r) {
            if (l == r) {
                ans++;
                r--;
                l++;
            } else {
                if (people[l] + people[r] <= limit) {
                    ans++;
                    l++;
                    r--;
                } else {
                    ans++;
                    r--;
                }
            }
        }
        return ans;
    }
};

我们先给数组排序，因为每艘汽艇只能坐两个人，所以尽量让体重小的和体重大的配对，这样才是

最有利的方案。所以在左右两端设置指针，如果左右两个人的体重和满足条件，ans++，左右指针

向中间移动；当不满足条件时，那么体重大的只能自己坐一个汽艇，右指针移动。遍历统计答案

(注：当左右指针指向同一个人时，这个人只能独自坐一个汽艇，coding时需要注意不要叠加了这

个人的体重导致代码出错)

盛水最多的容器

class Solution {
public:
    int maxArea(vector<int>& height) {
        int ans = 0;
        for (int l = 0, r = height.size() - 1; r >= l;) {
            ans = max(ans, min(height[l], height[r]) * (r - l));
            if (height[r] > height[l])
                l++;
            else
                r--;
        }
        return ans;
    }
};

如上图，假设a和b之间的区域盛水量最大。指针从左右两边移动，移动的过程中左右指针一定有

一个先移动到a或b，假设左指针先移动到a，此时右指针移动到c；如果c的高度大于a，那么a~c的

盛水量一定大于a~b，这样不符合假设；如果c的高度小于a，那么右指针向左移动才可能找到更大

的盛水量，那么右指针一定不会错过b，所以一定不会错过正确答案的统计。 

供暖器

class Solution {
public:
    bool f(vector<int>& heaters, vector<int>& houses, int i, int j) {
        return j == heaters.size() - 1 ||
               abs(heaters[j] - houses[i]) < abs(heaters[j + 1] - houses[i]);
    }
    int findRadius(vector<int>& houses, vector<int>& heaters) {
        sort(heaters.begin(), heaters.end());
        sort(houses.begin(), houses.end());
        int ans = 0;
        for (int i = 0, j = 0; i < houses.size(); i++) {
            while (!f(heaters, houses, i, j))
                j++;
            ans = max(ans, abs(heaters[j] - houses[i]));
        }
        return ans;
    }
};

在house和heater数组分别设两个指针，同时移动；当house[i]和heater[j]的半径小于house[i]和

heater[j+1]的半径时，记录此时的半径，i移动下一个位置；i+1位置上的房子一定和j及其以后的位

置上的暖气产生最小半径，因为j之前的暖气和i位置上的房子没有产生最小半径，那么和i+1上的房

子更不可能产生最小半径

最小的整数

class Solution {
public:
    void swap(vector<int>& nums, int l, int r) {
        int rem = nums[l];
        nums[l] = nums[r];
        nums[r] = rem;
    }
    int firstMissingPositive(vector<int>& arr) {
        int l = 0, r = arr.size();
        while (l < r) {
            if (arr[l] == l + 1)
                l++;
            else if (arr[l] > r || arr[l] <= l || arr[arr[l] - 1] == arr[l])
                swap(arr, l, --r);
            else
                swap(arr, l, arr[l] - 1);
        }
        return l + 1;
    }
};

  此题就比较难了；首先关于l和r指针的定义：l就是在遍历数组，r第一个意义就是r包括r之后的区

域是一个"垃圾区"，用来收集前面重复或不需要的数字；第二个意义就是r表示r之前最大还有可能

填上的数字。

  当l位置上的数字就是l+1时，l移动

  当l位置上的数字大于r时，因为最大就填到r，所以也不需要了；arr[l]<=l同理

  当arr[arr[l]-1]==arr[l]时，即在arr[l]-1位置上已经有了arr[l]这个数字，那也就不需要这个数字了

  当以上条件都不满足时，那就把arr[l]放到正确的位置arr[l]-1上

最后l位值本应对应的数字l+1就是缺失的数字