穿越雷区（bfs）

1.题目链接https://www.lanqiao.cn/problems/141/learning/?page=1&first_category_id=1&sort=students_count&second_category_id=3&status=2

2.题目分析

由题，显然是一道典型的搜索题。这里我使用的广度优先搜索，不过限制条件比较特殊，是每次只能走不同符号的地方，不过也很好解决，在结构体新加一个属性就可以解决。剩下的就是常规的bfs模版了。

3.代码实现

#include<iostream>
#include<queue>
using namespace std;
char map[101][101];
int n;
int book[101][101];
int nextgo[4][2] = { 0,1,1,0,0,-1,-1,0 };
int start_x, start_y, end_x, end_y;
typedef struct Node
{
	int x, y, step;
	char flag;
}node;
int bfs(int x, int y)
{
	queue<node>q;
	q.push({ x,y,0,'.' });
	while (q.size())
	{
		node d = q.front();
		q.pop();
		if (d.x == end_x && d.y == end_y)
		{
			return d.step;
		}
		for (int i = 0; i < 4; i++)
		{
			int tx = d.x + nextgo[i][0];
			int ty = d.y + nextgo[i][1];
			if (tx >= 0 && tx < n && ty >= 0 && ty < n && !book[ty][tx])
			{
				if (d.flag != map[ty][tx])
				{
					book[ty][tx] = 1;
					q.push({ tx,ty,d.step + 1,map[ty][tx] });
				}
			}
		}
	}
	return -1;
}
int main()
{
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		for (int j = 0; j < n; j++)
		{
			cin >> map[i][j];
			if (map[i][j] == 'A')
			{
				start_x = j;
				start_y = i;
			}
			if (map[i][j] == 'B')
			{
				end_x = j;
				end_y = i;
			}
		}
	}
	book[start_y][start_x] = 1;
	cout << bfs(start_x, start_y);
	return 0;
}

具体代码实现如上，接下来对每个操作进行解释。

这是对每个节点属性的创建，记录了该点的坐标以及走到该点需要的步数，还有flag记录该点的符号，便于之后进行判断。

bfs函数的开头，先创建一个队列，然后把起始位置存进去。

之后在队列不为空的基础上对队列首个元素依次进行分析，如果该元素的坐标就是终点坐标，我们就可以返回该坐标的步数。

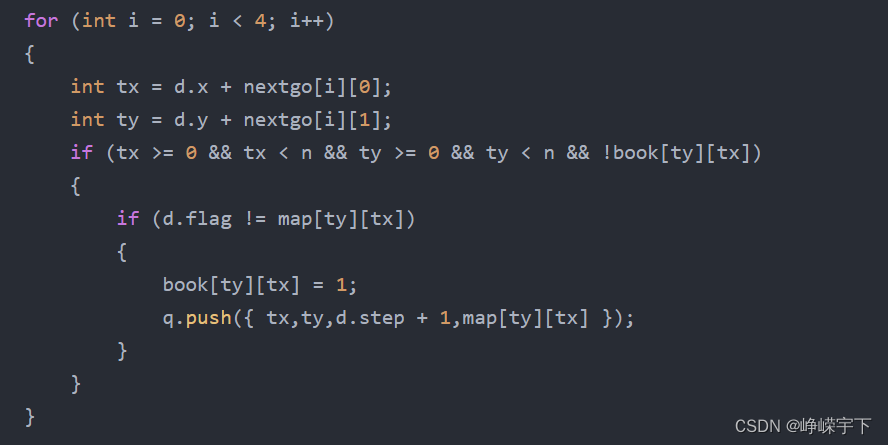
然后就是正常的搜索操作，不过额外加了一个判断（如下），寻找与该节点符号不同的节点，从而进行下一步搜索。