【PTA】图的邻接矩阵存储和遍历

最新推荐文章于 2024-11-03 10:45:48 发布

原创最新推荐文章于 2024-11-03 10:45:48 发布 · 1.6k 阅读

23 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法

PTA 专栏收录该内容

16 篇文章

订阅专栏

1. 题目描述

图的邻接矩阵存储用一个一维数组存储各顶点数据元素，一个二维数组存储顶点之间的邻接关系。

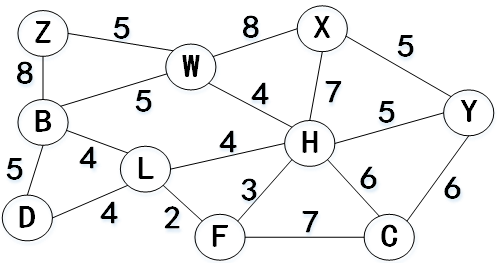
如上面的无向加权图，顶点数据元素为“A-Z”之间的单个字符，为了使遍历输出结果唯一，要求顶点数据元素按由小到大(ASCII码)的顺序存储。例如，对于上面的加权图，数据元素按照B、C、D、F、H、L、W、X、Y、Z的顺序存储。依附于边的权值为整数，且大于0。使用C或C++编写算法，实现：
（1）使用邻接矩阵存储结构，按照输入数据建立加权图；
（2）按存储位置，从第1个顶点出发，按照深度优先搜索算法输出各顶点数据；
（3）按存储位置，从第1个顶点出发，按照广度优先搜索算法输出各顶点数据；
（4）按存储位置，计算并输出个顶点的度。

1.1 输入格式

输入分为以下几行，第1行为图的顶点数，第2行为图的边数，第3行及以后各行为图的各个边依附的顶点及其权值。

1.2 输出格式

输出分为以下行，第1行为深度优先遍历序列，第2行为广度优先遍历序列，其后为各顶点及其度。

1.3 输入样例

如上图的输入格式为：

10
17
Z B 8
Z W 5
B D 5
B W 5
B L 4
D L 4
W X 8
W H 4
L H 4
L F 2
X H 7
X Y 5
H F 3
H Y 5
H C 6
F C 7
C Y 6

1.4 输出样例

如上图的输出为：

DFS: B D L F C H W X Y Z
BFS: B D L W Z F H X C Y
B:4
C:3
D:2
F:3
H:6
L:4
W:4
X:3
Y:3
Z:2

其中"DFS:","BFS:","B:","C:"等为提示标志，序列" B D L F C H W X Y Z"的每个字符前面有一个空格。

代码长度限制：16 KB

时间限制：400 ms

内存限制：64 MB

栈限制：8192 KB

2. 图的邻接矩阵存储结构

2.1 存储方式

用连续的地址空间存储图的数据元素及元素之间的关系（邻接关系）。

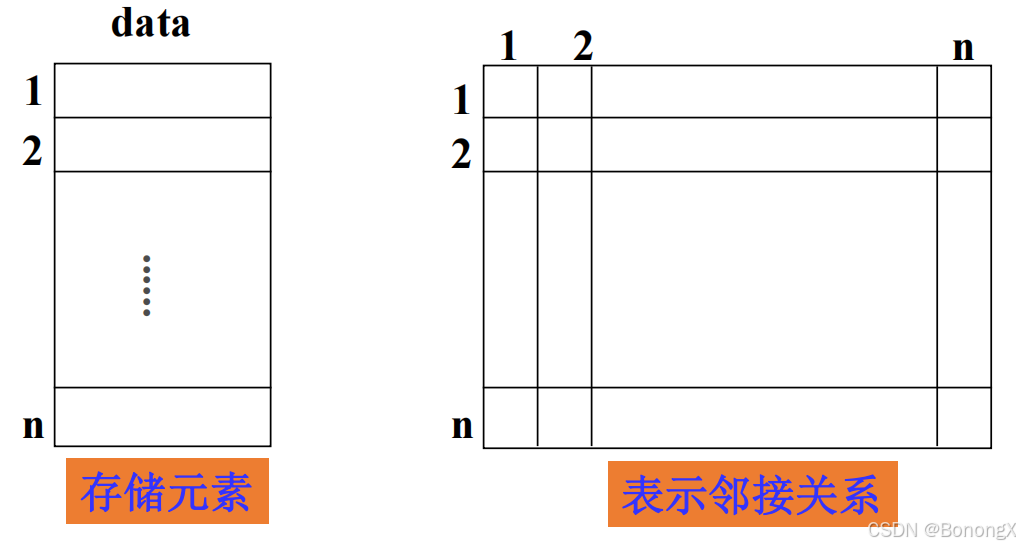
$Edge[i][j]=\left\{\begin{matrix} 1, \, & \left \langle v_{i},v_{j} \right \rangle \in E \; or\; \left ( v_{i},v_{j} \right )\in E\\ 0,\; &else \end{matrix}\right.$

$Edge[i][j]=\left\{\begin{matrix} W_{ij},\; v_{i}\neq v_{j}\; and\; \left \langle v_{i},v_{j} \right \rangle \in E\; or\; \left ( v_{i},v_{j} \right ) \in E& \hfill\\ \infty ,\; v_{i}\neq v_{j}\; and\; \left \langle v_{i},v_{j} \right \rangle \notin E\; or\; \left ( v_{i},v_{j} \right ) \notin E \hfill \\ 0,\; v_{i}= = v_{j} \hfill\hfill\\ \end{matrix}\right.$

2.2 举例

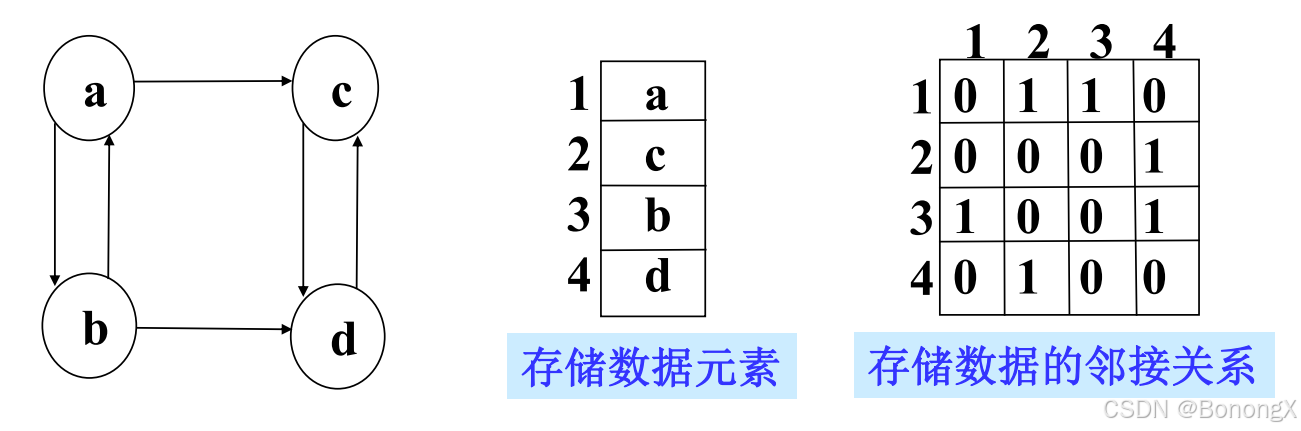
2.3 特点

对于无向图（非加权）

① 矩阵是对称的；

② 第 i 行或者第 i 列1的个数为顶点 $v_{i}$ 的度；

③ 矩阵中1的个数的一半为图中边的数目；

④ 很容易判断顶点 $v_{i}$ 和顶点 $v_{j}$ 之间是否有边相连。

对于有向图（非加权）

① 矩阵不一定是对称的；

② 第 i 行中1的个数为顶点 $v_{i}$ 的出度；

③ 第 i 列中1的个数为顶点 $v_{i}$ 的入度；

④ 矩阵中1的个数为图中弧（有向边）的数目；

⑤ 很容易判断顶点 $v_{i}$ 和顶点 $v_{j}$ 之间是否有弧相连。

3. 图的遍历

3.1 图的遍历概述

遍历：从已给的连通图中某一顶点出发，沿着一些边访遍图中所有的顶点，且使每个顶点仅被访问一次，就叫做图的遍历，它是图的最重要的基本运算。

遍历图的实质：找每个顶点的邻接点并访问的过程。

注意：图的遍历比树更复杂，因为元素之间的关系复杂。

要考虑两种情况：

其一：可能会陷入死循环（如图中存在环）

其二：可能有的顶点不能从出发点访问到（如非连通图）

处理的方法是：对每个顶点作一个访问标志！

设置一个辅助数组 $visited[n]$ ，用来标记每个被访问过的顶点。它的初始状态为0，在图的遍历过程中，一旦某一个顶点 $v_{i}$ 被访问， $visited[i]$ 置为1，防止它被多次访问。

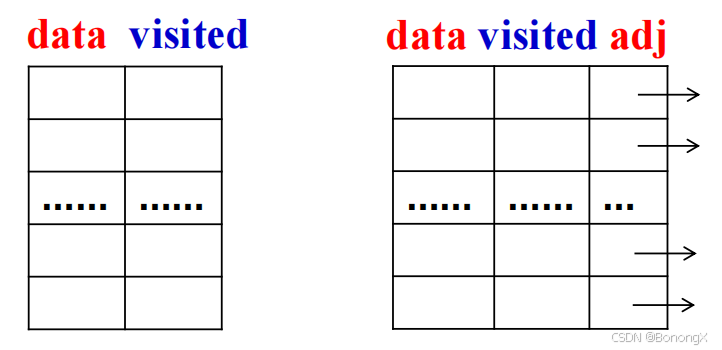
3.2 图的深度优先遍历：DFS

3.2.1 遍历方式

假设图为G=(V,E)，从 $v_{0}$ 开始深度优先遍历图

• 访问 $v_{0}$ ，作已访问标志；

• 选择一个与 $v_{0}$ 邻接但未访问的顶点 u（如果没有，则从 $v_{0}$ 开始的深度优先遍历结束；如果有多个，选其中一个）；

• 从顶点u开始深度优先遍历图；

3.2.2 特点

类似于树的前序遍历；

沿着图的某一分支访问，直到它的末端，然后回溯。

3.2.3 算法

/* Visited[]为全局变量，已经初始化为false */
void DFS(Graph G, Vertex V, void (*Visit)(Vertex))
{ 
    // 从第V个顶点出发递归地深度优先遍历图G
    Visit( V ); // 访问第V个顶点 
    Visited[V] = true;
    for(V的每个邻接点W){
        if (!Visited[W]){
        // 对V的尚未访问的邻接顶点W递归调用DFS
        DFS(G, W, Visit);
        }
    }
}

3.3 图的广度优先遍历：BFS

3.3.1 遍历方式

假设图为G=(V,E)，从 $v_{0}$ 开始深度优先遍历图

• 访问 $v_{0}$ ，作已访问标志；

• 依次访问与 $v_{0}$ 邻接但未访问的各个顶点；

• 再依次访问这些顶点的未被访问的邻接点。

3.3.2 特点

类似于树的层序遍历；

尽可能先在横向上访问邻接点，即由近及远，依次访问和出发点有路径相通，且路径长度为1, 2, ...的顶点。

3.3.3 算法

bool IsEdge(MGraph Graph, Vertex V, Vertex W){
    return Graph->G[V][W]<INFINITY ? true : false;
}

// Visited[]为全局变量，已经初始化为false
void BFS(MGraph Graph, Vertex S, void(*Visit)(Vertex)) { 
    // 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 
    Queue Q; 
    Vertex V, W;
    Q = CreateQueue(MaxSize); 
    // 创建空队列, MaxSize为外部定义的常数
    // 访问顶点S：此处可根据具体访问需要改写 
    Visit(S);
    Visited[S] = true; // 标记S已访问 
    AddQ(Q, S); // S入队列 
    while(!IsEmpty(Q)) {
        V = DeleteQ(Q); // 弹出V 
        for(W=0; W<Graph->Nv; W++) {
        // 对图中的每个顶点W ,若W是V的邻接点并且未访问过 
            if(!Visited[W] && IsEdge(Graph, V, W)) {
                // 访问顶点W 
                Visit( W );
                Visited[W] = true; // 标记W已访问 
                AddQ(Q, W); // W入队列 
            }
        }
    } // while结束
}

4. 代码实现

// Creator: Bonong
// Create Time: 2024/11/1 16:00
// Description: 图的邻接矩阵存储和遍历

#include <iostream>
using namespace std;

// 定义常量
#define maxSize 26
#define INFINITY 65535

// 图的邻接矩阵存储
typedef struct GNode {
    int vertexNum; // 顶点数
    int edgeNum; // 边数
    int edge[maxSize][maxSize]; // 邻接矩阵
    char data[maxSize]; // 存顶点的数据
}GNode, *PtrToGNode;

// 创建图
PtrToGNode CreatGraph(int vertexNum) {
    PtrToGNode Graph = new GNode;
    Graph->vertexNum = vertexNum;
    Graph->edgeNum = 0;
    // 初始化邻接矩阵
    for (int v = 0; v < maxSize; v++) {
        Graph->data[v] = '$';
        for (int w = 0; w < maxSize; w++) {
            Graph->edge[v][w] = INFINITY;
        }
    }
    return Graph;
}

// 构建图
PtrToGNode BuildGraph() {
    PtrToGNode Graph;
    int vertexNum;
    cin >> vertexNum;
    Graph = CreatGraph(vertexNum);
    cin >> Graph->edgeNum;
    if (Graph->edgeNum != 0) {
        char v1, v2;
        int weight;
        for (int i = 0; i < Graph->edgeNum; i++) {
            cin >> v1 >> v2 >> weight;
            int v = v1 - 'A'; 
            int w = v2 - 'A';
            Graph->data[v] = v1;
            Graph->data[w] = v2;
            Graph->edge[v][w] = weight;
            Graph->edge[w][v] = weight;
        }
    }
    return Graph;
}

// 深度优先遍历图
void DFS(PtrToGNode Graph, int v, bool visited[]) {
    while(Graph->data[v] == '$') {
        v++;
    }
    cout << " " << Graph->data[v];
    visited[v] = true;
    for (int w = 0; w < maxSize; w++) {
        if (Graph->edge[v][w] != INFINITY && !visited[w]) {
            DFS(Graph, w, visited);
        }
    }
}

// 广度优先遍历图
void BFS(PtrToGNode Graph, int v, bool visited[]) {
    int queue[maxSize];
    int front = 0, rear = 0;
    while(Graph->data[v] == '$') {
        v++;
    }
    cout  << " " << Graph->data[v];
    visited[v] = true;
    queue[rear++] = v; // 入队
    while (front != rear) {
        int w = queue[front++]; // 出队
        // 遍历w的邻接点
        for (int x = 0; x < maxSize; x++) {
            if (Graph->edge[w][x] != INFINITY && !visited[x]) {
                cout  << " " << Graph->data[x];
                visited[x] = true;
                queue[rear++] = x;
            }
        }
    }
}

// 计算顶点的度
int GetDegree(PtrToGNode Graph, int v) {
    int degree = 0;
    for (int w = 0; w < maxSize; w++) {
        if (Graph->edge[v][w] != INFINITY) {
            degree++;
        }
    }
    return degree;
}

int main() {
    // 创建图
    PtrToGNode Graph = BuildGraph();
    // 深度优先遍历
    bool visited[maxSize] = {false};
    cout << "DFS:";
    DFS(Graph, 0, visited);
    // 重置visited数组
    for (int v = 0; v < maxSize; v++) {
        visited[v] = false;
    }
    // 广度优先遍历
    cout << endl << "BFS:";
    BFS(Graph, 0, visited);
    cout << endl;
    // 计算并输出顶点的度
    for(int v = 0; v < maxSize; v++) {
        if(Graph->data[v] != '$') {
            cout << Graph->data[v] << ":" << GetDegree(Graph, v) << endl;   
        }
    }
    return 0;
}