swust oj 1015: 堆排序算法

堆的概念

堆(Heap)是计算机科学中一类特殊的数据结。堆通常是一个可以被看作一棵完全二叉树的数组对象。可以理解为堆就是一颗用数组是实现的完全二叉树。

性质

• 堆中某个结点的值总是不大于或不小于其父结点的值；

• 堆总是一棵完全二叉树

将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。

下标的关系

• 父亲的下标为i
• 左孩子的下标为2*i+1
• 右孩子的下标为2*i+2

 堆的实现

堆向下调整算法

前提：左右子树都是一个堆，才能进行调整

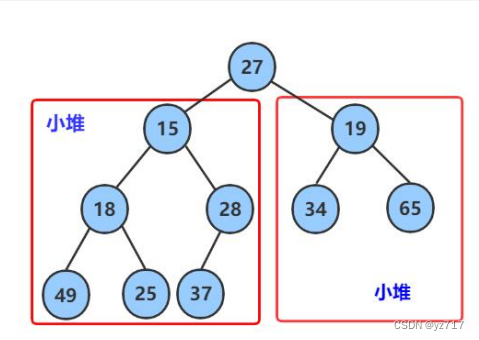
算法思想 

找出左右孩子中最小的一个，与父亲进行比较

若小于父亲，二者交换位置，更新父亲结点，孩子结点

一直重复上述过程

若不小于父亲说明建堆完成

代码实现 

void Adjustdown(datatype* arr, int n, int root)//向下调整
{
	//前提：左右子树已经是小堆
	//找出左右孩子中小的那个
	int parent = root;
	int child = root * 2 + 1;//假设小的那个是左孩子
	while (child < n)
	{
		if (child+1<n&&a[child + 1] < a[child])++child;//找出小的那个孩子 
		//child+1判断特殊情况
		//即child为左孩子且为叶子节点且不存在右孩子 
	

		//如果父亲大于孩子则交换
		if (arr[child] < arr[parent])
		{
			swap(arr[child], arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

建堆过程

仅需从倒数第一个非叶子结点开始开始调整

代码实现

	for (int i = (n - 1-1)/2; i >= 0; i--)
	{
		adjust_down(arr, i, n);
	}

题目描述

其实就是一个建堆的过程，故题解代码如下

题目代码

#include <iostream>
using namespace std;
int arr[1000];

void adjust_down(int* arr, int root,int n)
{
	int parent = root;
	int child = parent * 2 + 1;
	while (child < n)
	{
		if (child + 1 < n && arr[child + 1] < arr[child])child++;
		if (arr[child] < arr[parent])
		{
			swap(arr[child], arr[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}


int main()
{
	int n;
	cin >> n;
	for (int i = 0; i < n; i++)cin >> arr[i];
	for (int i = (n - 1-1)/2; i >= 0; i--)
	{
		adjust_down(arr, i, n);
	}
	for (int i = 0; i < n; i++)cout << arr[i] << ' ';
	return 0;
}