1035 插入与归并 - PAT（Basic Level）Practice（通俗易懂，小白也能学会的简单方法）

题目描述：

根据维基百科的定义：

插入排序是迭代算法，逐一获得输入数据，逐步产生有序的输出序列。每步迭代中，算法从输入序列中取出一元素，将之插入有序序列中正确的位置。如此迭代直到全部元素有序。

归并排序进行如下迭代操作：首先将原始序列看成 N 个只包含 1 个元素的有序子序列，然后每次迭代归并两个相邻的有序子序列，直到最后只剩下 1 个有序的序列。

现给定原始序列和由某排序算法产生的中间序列，请你判断该算法究竟是哪种排序算法？

输入格式：

输入在第一行给出正整数 N (≤100)；随后一行给出原始序列的 N 个整数；最后一行给出由某排序算法产生的中间序列。这里假设排序的目标序列是升序。数字间以空格分隔。

输出格式：

首先在第 1 行中输出Insertion Sort表示插入排序、或Merge Sort表示归并排序；然后在第 2 行中输出用该排序算法再迭代一轮的结果序列。题目保证每组测试的结果是唯一的。数字间以空格分隔，且行首尾不得有多余空格。

输入样例 1：

10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0

输出样例 1：

Insertion Sort
1 2 3 5 7 8 9 4 6 0

输入样例 2：

10
3 1 2 8 7 5 9 4 0 6
1 3 2 8 5 7 4 9 0 6

输出样例 2：

Merge Sort
1 2 3 8 4 5 7 9 0 6

上代码：

#include<bits/stdc++.h>
using namespace std;
int M[110], Mc[110];//原序列，排序后序列
set<int>s;//若归并排序，则需得出归并的次数
int main()
{
    int N, k1 = 0, k2 = 0, i;
    cin >> N;
    for(i = 0; i < N; i++) cin >> M[i];
    cin >> Mc[0];
    for(i = 1; i < N; i++)
    {
        cin >> Mc[i];
        if(Mc[i] < Mc[i - 1] && !k1) k1 = i;
        if(Mc[i] != M[i] && k1) k2 = 1;
    }
    s.insert(k1);
    if (!k2)
    {
        puts("Insertion Sort");
        sort(Mc, Mc + k1 + 1);
    }
    else
    {
        puts("Merge Sort");
        for(i = k1 + 1; i < N; i++) {if (Mc[i] < Mc[i - 1]) {s.insert(i - k1); k1 = i;}}
        int n = *s.begin() * 2;
        for(i = 0; i + n < N; i += n) sort(Mc + i, Mc + i + n);
        sort(Mc + i, Mc + N);
    }
    cout << Mc[0];
    for(i = 1; i < N; i++) cout << " " << Mc[i];
    puts("");
    return 0;
}

详解：

  题目保证每组测试的结果是唯一的，故判断为一种后就不用去判断第二种，所以首要目标是得出哪一种好判断。

  这里我推荐不懂归并排序的可以去看NoobDream_的讲解，下图为其文的归并讲解图。

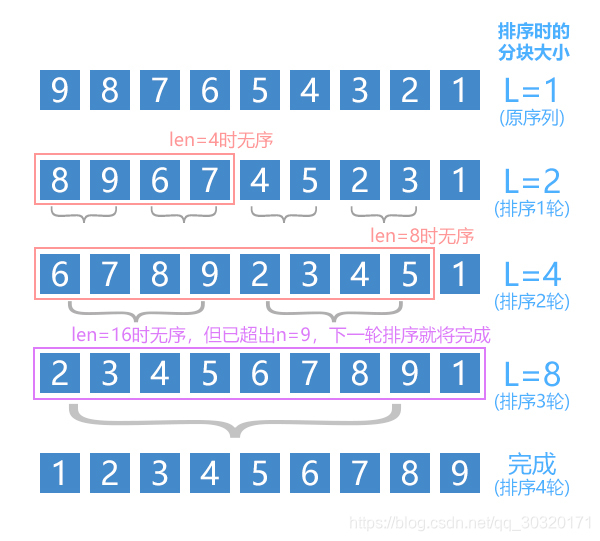
  这里不难看出归并是较为复杂的，所以我选择先判断插入。

  插入排序相对好理解一些，经过思考，我们能得出关于插入排序的重要结论：插入排序后，前k1个数字排序完成，后N-k1个数字与原序列相等。

  这样就好理解了，代码第15行的k2就是起判断其是否是插入排序的作用，只要后面N-k1个数字存在与原序列不等的情况，就必定不是插入排序。

  如果是插入排序，那问题就很简单了，只需要给排序后序列的前k1个数字排序就可以了（sort函数不会用的人有难了）。

  如果是归并排序，那么这个问题就比较复杂了，因为会出现k1（给不懂的人解释一下，在26行以前，k1一直是排序后序列的直到第一个小于前一个数字的数字出现前已经排序完美的数字个数）并非是原排序排序后的已排序归并数字个数，也会出现排序所需组数不足的情况，不懂的话理解为有超级多坑就行了。

  此时，我选择用set<int>来得出已排序归并数字个数，set是个好东西，既不会重复插入同一个数字，还能自动从小到大排序，不过记得加*才是set里的数字，否则只是那个数字的地址。

  然后排序上问题只要注意一下最后一组就行了，我是直接拎出来单独写一行（29行），其他的各位读者想必都看得懂（看不懂的去狠狠恶补函数去吧），我就不多加赘述。

  祝各位码农身体健康，万事如意！