关于求方程近似根的方法探寻问题_涵数的近似根-优快云博客

本文链接：https://blog.youkuaiyun.com/2301_79105088/article/details/134900423

一、内容简述

本文会使用构造压缩函数、二分法和牛顿切线法三种方法求方程x^2+x-1=0在（0,1）上的根。在编程语言上，我们会使用matlab画图，还会在c语言的基础上进行代码分析，此外还有python语言。我们首先通过matlab画图来求出该方程的近似解，然后再用三种方法分别求解，并与这个近似解进行比对。

下面我先用matlab画图求得这个方程的近似解：

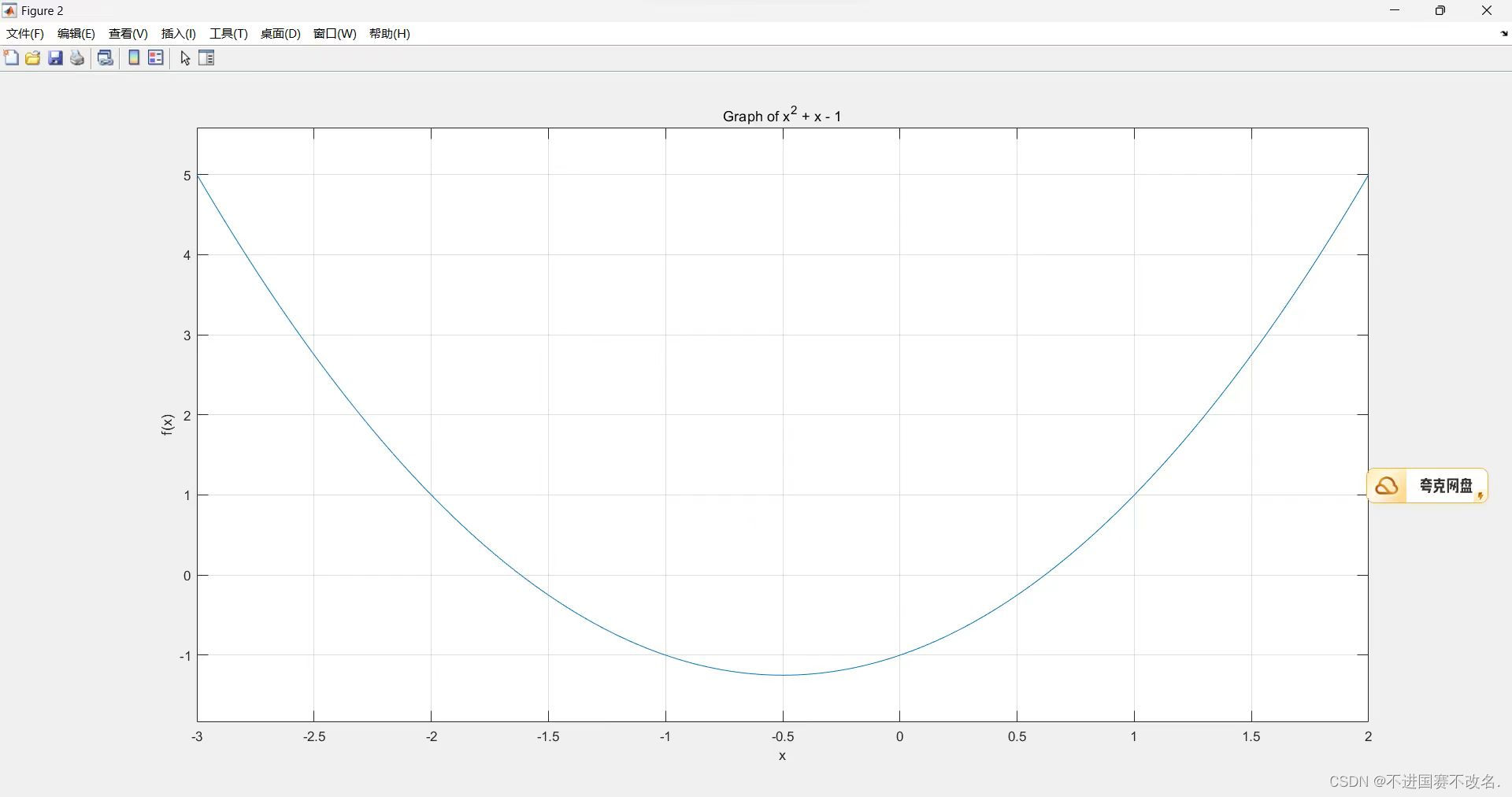
要求该方程的根，只需要求解该方程和y=0这个方程的交点这个位置便可以得出方程的近似解。

在该图像的不断放大、坐标区间不断缩小的过程中，可以确定该方程在（0,1）上的根位于 0.6180~0.6181之间。

接着，我们便会使用这个近似解对代码的正确性进行验证。

二、3种求解方法

1. 构造压缩函数

1.1 基础知识

压缩映射原理就是解决某类映射不动点的存在性和唯一性的问题,利用它的这一特性便是解决方程根的关键。那么什么是不动点呢？听听老师的简单例子，便可以理解了：在一个地方打开一张世界地图，上面有一个点，它在地图上的位置和它的实际位置是重叠的。（不动点的证明在这里不再展开）为了使用压缩映射来求解方程的根,我们需要将原方程转化为一个适合进行压缩映射的形式。我们可以通过变形、代换等方法将方程转化为映射的形式。具体来说,我们可以将方程表示为x=
g(x),其中g(x)是一个映射函数。

1.2 代码实现

在 MATLAB 中，可以使用 fzero 函数来求解方程。对于方程 x^2+x-1=0，我们可以这样使用 fzero:

%定义方程
equation = @(x)x^2 +x- 1;
%设置初始猜测值
initialGuess=1;

%使用fzero求解方程
root = fzero(equation,initialGuess);
%显示结果
disp([方程的根为:num2str(root)]);

其中，equation 是方程的匿名函数表示，initialGuess 是方程的根的初始猜测值，fzero 函数会尝试找到方程的根，并将结果存储在变量 root 中，最后，通过 disp 函数显示方程的根。

请注意，初始猜测值对于 fzero 函数来说是重要的，因为它会影响算法的收敛性。在这个例子中，我们选择了 1 作为初始猜测值。你可以根据实际情况选择不同的初始猜测值，以提高算法的性能。

在 MATLAB 中，fzero 是一个强大的工具，适用于各种方程的数值求解。

在编译器上的运行结果为：

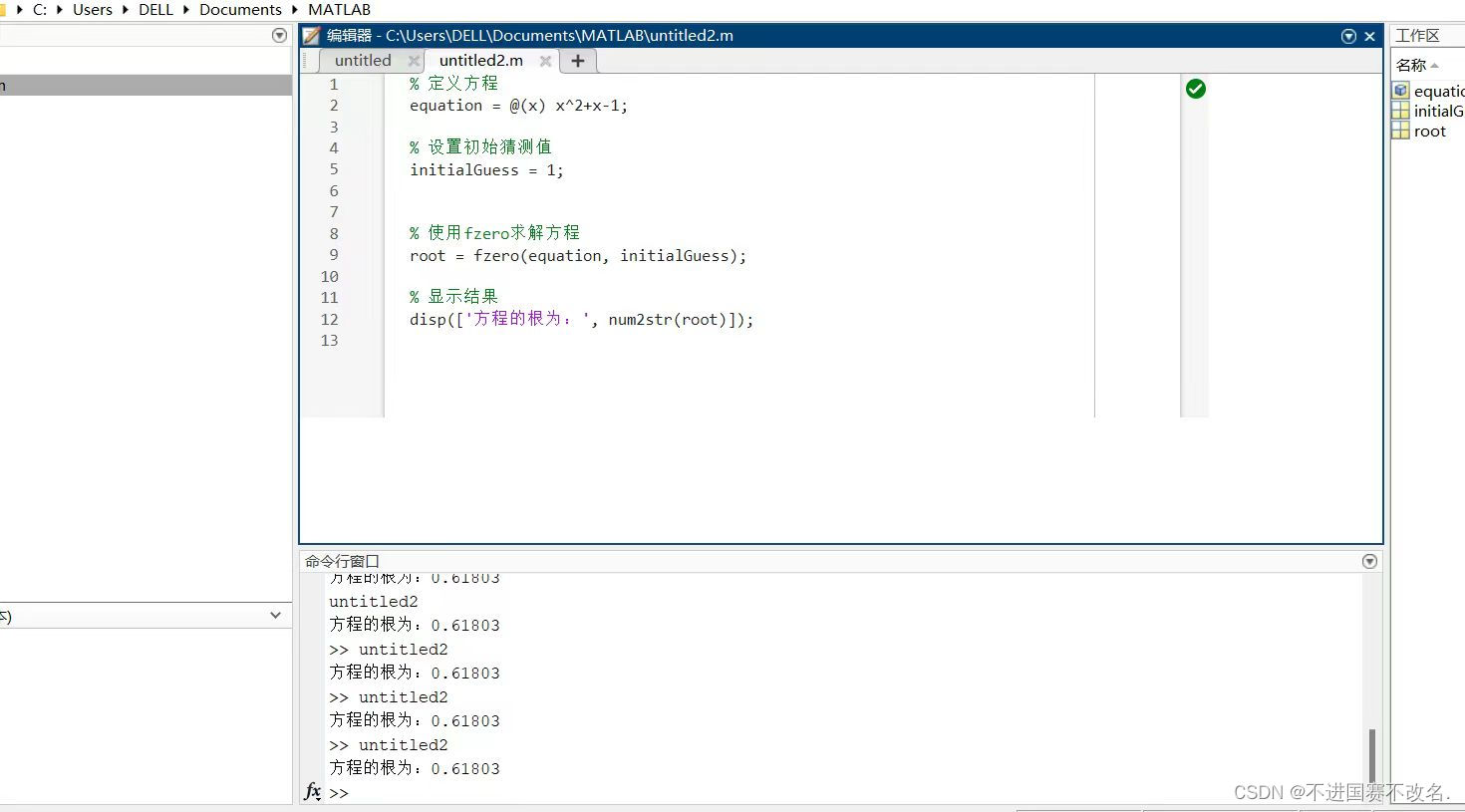
我们发现，matlab默认保留的小数只有5位。

下面我们用c语言程序再次对该方程进行求解。

具体代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <math.h>
int main()
{
	float x = 0.0;
	double x0 = 0.0;
	double f1 = x * x + x - 1;
	printf("请输入一个近似值\n");
	double f2 = sqrt(1-x);
	scanf("%f", &x);
	do
	{
		x0 = x;
		x = sqrt(1-x);

	} while (fabs(x - x0) >= 1e-8);
	printf("该方程组的解是%f\n", x);
	
	return 0;
}

我们通过一个简单的迭代公式来逐步求解方程的根。首先，按照公式算出x1 = g(x0)，然后再用同样的方法算出x2，以此类推。这样一直迭代下去，就可以逐渐接近方程的根了。这个过程就像是一个魔法棒，每次点击都能让你离目标更近一步。

当满足迭代我们设置的停止条件时，程序自然就会停止。

对于小数保留的位数的探讨将在下面的二分法里具体说明。

2. 二分法

1.1 基础知识

二分法这个方法无论是在数学中，还是在解一个算法题中，都是一个比较重要的知识点。

首先要讲的便是二分法求方程根的思想：

我们知道，一个连续函数，如果两个不同点的函数值的乘积为负数，那么在这两个点之间的区间内至少有一个根。这便是解决方程根的关键。

以我们求的x^2+x-1=0在（0,1）上举个例子：

令f(x)=x^2+x-1, 容易知道f(0)<0, f(1)>0 ,所以在（0,1）上必然存在与y=0 的交点，即存在根，然后再取该区间的中点0.5，然后计算x=0.5时的函数值，如果在0.5时的函数值大于0，那么该根一定存在于（0,0.5）之间，否则在（0.5,1）之间，以此类推，不断缩小区间，便可以求出方程的近似解。

在解决这个问题中，如果是人为计算，那么肯定是非常难的，但是交给计算机来计算，就仅仅是几行代码的问题。

1.2 代码实现

#include<iostream>
using namespace std;
int main(){
	double low=0.0,high=1.0,cnt=0;
	double middle=0.5;
	double y=middle*middle+middle-1;
	while(cnt<=100000){
		if(y==0){
			break;
		}
		if(y<0){
			low=middle;
			middle=(low+high)/2;
		}
		else{
			high=middle;
			middle=(low+high)/2;
		}
		y=middle*middle+middle-1;
		cnt++;
	}
	printf("%.49lf",middle);
	return 0;
}

代码实现便是应用了二分法的基本知识进行了一个代码化，这里就不多赘述了。

其中有一点，我在最后一句代码中表明printf("%.49lf",middle);意思是求保留49位小数。

竟然能保留到49位小数！那么我为什么在这个里写代码让他保留49位小数呢？因为我发现一个问题，无论让他进行多少轮循环，如果超过49位之后，后面多出来的小数竟然都是0，正如下面这样：

我不太清楚这到底是因为什么，但是他能保留49位就已经足够强大了！

这里可以看出求出的解和正确解非常吻合，甚至比画图中的近似解更加精准。

这样便验证了该方法的可行性，也验证了过程的正确性。

此外，我们还用python实现该方法：

具体，在这里我就再不一一赘述。

3.牛顿切线法

1.1 基础知识

我们设方程函数f(x)=m,该方程可以转化为g(x)=f(x)-m=0,我们只需要求出函数g(x)=0的解，就可以求出f(x)=m的解。

首先，我们需要找到函数f(x)的导数，然后用牛顿切线法来找到与x轴的交点。

但是，你要求的是绘制函数f(x)=x^2+x-1的曲线图像，这个函数在实数域上是连续的，且在x=1和x=-1处与x轴相交。我们可以用plot函数直接绘制这个函数的图像。

对于我们要求的方程x^2+x-1=0根，我们先找到了一个Xn点，我们在f(Xn)处进行求导取得了它的切线。显然只要这个切线的斜率不为0，那么我们一定可以获得它和x轴的交点。我们将这个交点作为下一个取值，也就是Xn+1的点。我们重复上述过程进行迭代，很快就可以得到一个足够接近的解。

1.2 代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <math.h>
int main()
{
	float x = 0.0;
	double x0 = 0.0;
	double f1 = x * x + x - 1;
	printf("请输入一个近似值\n");
	double f2 = sqrt(1 - x);
	scanf("%f", &x);
	do
	{
		x0 = x;
		x = sqrt(1 - x);

	} while (fabs(x - x0) >= 1e-8);
	printf("该方程组的解是%.49lf\n", x);

	return 0;
}

牛顿迭代法和二分法有不少相似之处，下面是该代码的运行结果：