汉诺塔问题，递归（c语言）

汉诺塔，，是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

那么汉诺塔的底层逻辑是什么呢？

首先要清楚我们有A,B,C三根柱子，目的是将A柱子上的汉诺塔移动到C柱子上。我们可以依靠B柱子起到中转的作用，在B柱子上建立一个小的汉诺塔，这时候A柱子上便剩下最底层最大的盘子，再将这个盘子移动到C柱子上。这时候B柱子上的汉诺塔成为起始点，A柱子成为中转战，C柱子为目的地。依次类推，最终成功将汉诺塔从A柱子移至C柱子。

下面为三层汉诺塔的解法

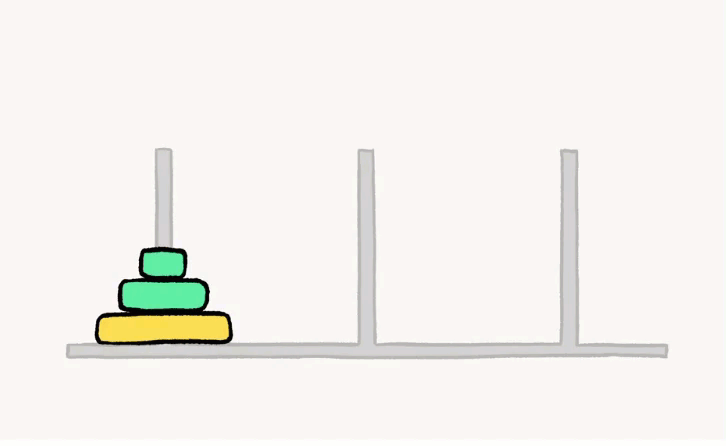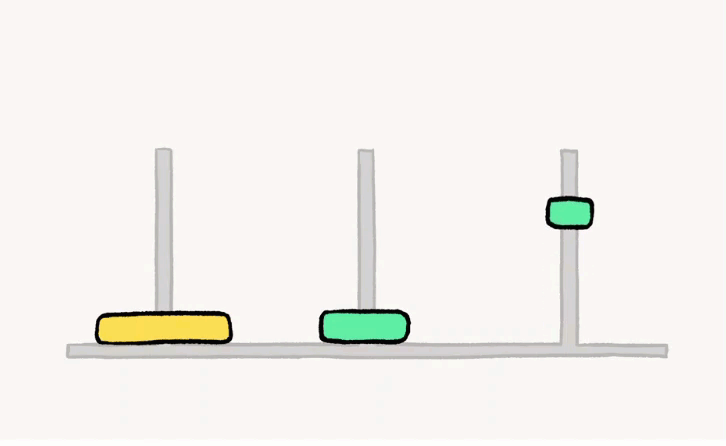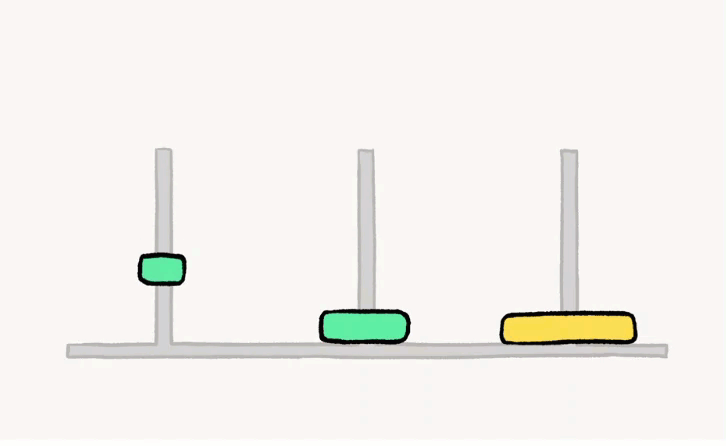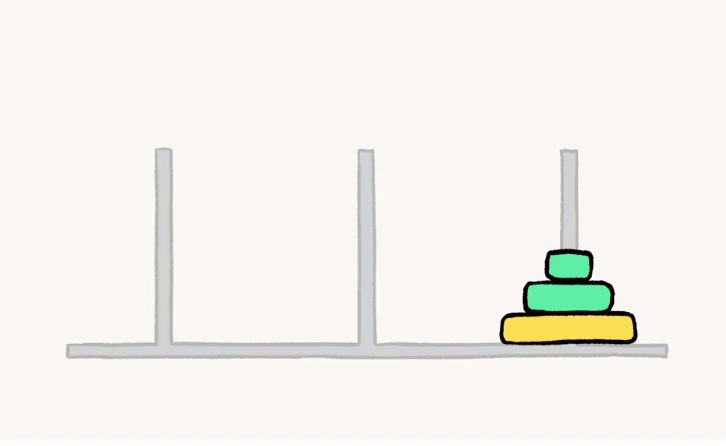
如果是4层，5层，6层甚至传说中的64层呢？那么层数的增i加也意味着解法的次数增加。1层汉诺塔的次数为1，2层的次数为3，3层的次数为7，4层的次数为15，不难发现，n层汉诺塔的最少移动次数为2^n-1次。

那么我们如何通过c语言实现汉诺塔问题呢？可以通过函数和递归的方法。

1.先定义有n层汉诺塔，A柱为begin，B柱为mid,C柱为end

2.建立if语句实现递归，分为只有一层和≥一层

3.n-1层则需从A->C->B,然后将n层从A->C

代码如下

void hanoi(int n, char begin, char mid, char end)
{
	if (n == 1)
	{
		move(n, begin, end);
	}
	else
	{
		hanoi(n - 1, begin, end, mid);
		move(n, begin, end);
		hanoi(n - 1, mid, begin, end);
	}
}

再建立一个move函数来打印我们的步骤

全部代码如下

#include<stdio.h>

void move(int n,char begin,char end)
	{
	printf("将%d从%c移动到%c\n", n, begin, end);
	}
void hanoi(int n, char begin, char mid, char end)
{
	if (n == 1)
	{
		move(n, begin, end);
	}
	else
	{
		hanoi(n - 1, begin, end, mid);
		move(n, begin, end);
		hanoi(n - 1, mid, begin, end);
	}
}
int main()
{
	int n =0;
	printf("请输入:");
	scanf_s("%d", &n);
	
	hanoi(n, 'A', 'B', 'C');
	return 0;
}

结尾

通过汉诺塔，我们可以清楚了解到c语言中的递归，并运用到我们实际的运用当中。本篇为本人第一次尝试写文章，逻辑性没有那么严谨，有错误欢迎批评与指出，谢谢！