归并排序 快排优化

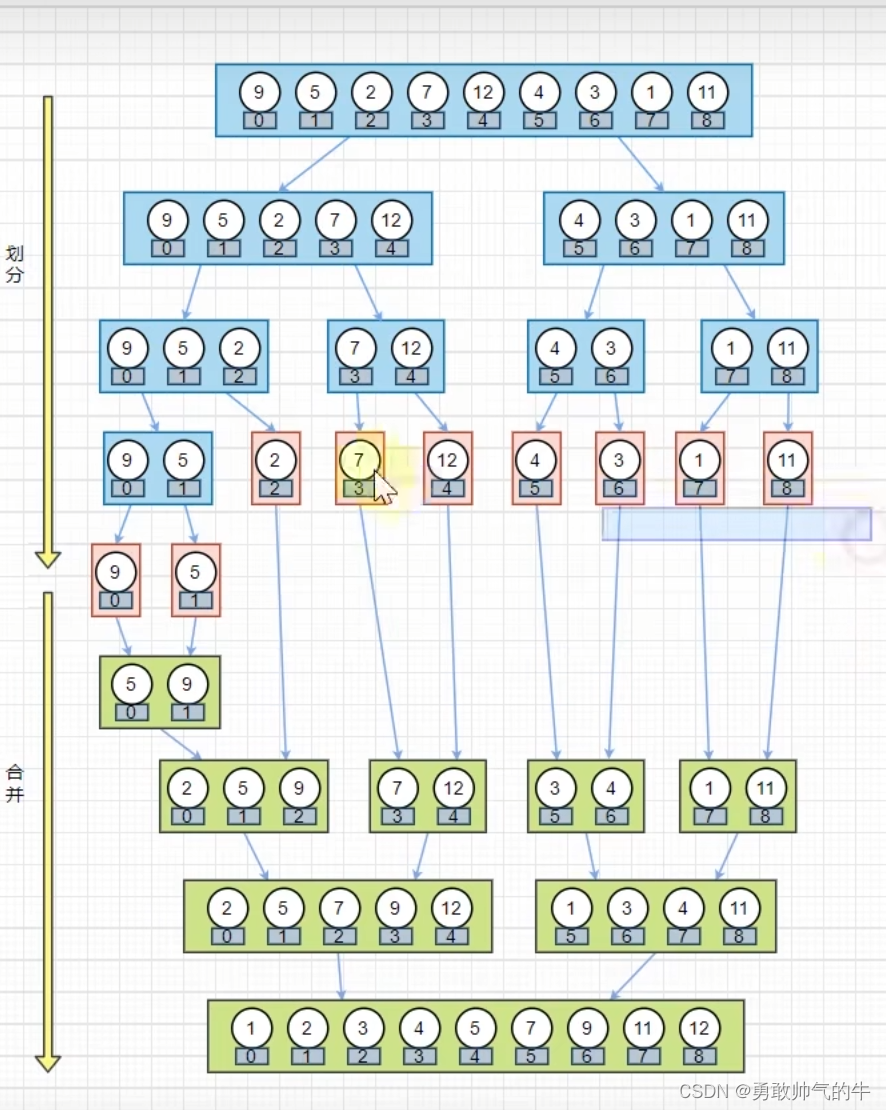
归并排序流程图

1.归并排序的思想

归并排序的具体步骤如下：

1. 分解：不断地将待排序的序列平均分割成子序列，直到每个子序列只包含一个元素。

2. 归并：从最小的子序列开始，两两合并，确保合并后的序列仍然有序。在归并过程中，需要额外的存储空间来存储合并后的序列。

3. 重复：重复归并步骤，直到最后只有一个有序的序列，这个序列就是排好序的结果。

归并排序的时间复杂度为 O(n \log n) O(nlogn)，是一种效率较高的排序算法。它不仅适用于小规模数据的排序，也能有效处理大规模数据集。此外，归并排序是一种稳定的排序算法，即相等的元素在排序后会保持其原有的顺序。

在实现归并排序时，通常采用递归或迭代两种方式。递归方式实现起来较为简洁，但需要额外的函数调用开销；而迭代方式虽然避免了递归的开销，但实现起来相对复杂。

#include<iostream>
#include<stdexcept>
#include<vector>
using namespace std;

//归并排序

//分治思想    分开-处理-合并


//合并数组
void merge(vector<int>&arr, int low, int mid, int high) {
	//计算左侧数组长度
	int left = mid - low + 1;
	//计算右侧数组长度
	int right = high - mid;

	//创建临时数组
	vector<int> L(left+1), R(right+1);

	//将分治开的左侧数组拷贝到新数组L中
	for (int i = 0; i < left; i++) {
		L[i] = arr[low + i];
	}
	//将分治开的右侧数组拷贝到新数组R中
	for (int j = 0; j < right; j++) {
		R[j] = arr[mid + 1 + j];
	}

	int i = 0;// 初始索引left子数组
	int j = 0; // 初始索引right子数组
	int k = low; // 初始索引合并的arr数组
	
	//对左右两边数组进行排序
	while (i < left && j < right) {
		//如果左边数组的值小于右边数组的值
		if (L[i] <= R[j]) {
			arr[k] = L[i];
			i++;
		}//如果右边数组的值小于左边数组的值
		else {
			arr[k] = R[j];
			j++;
		}
		k++;
	}
	//拷贝L的剩余元素
	while (i < left) {
		arr[k] = L[i];
		i++;
		k++;
	}
	while (j < right) {
		arr[k] = R[j];
		j++;
		k++;
	}


}


//递归排序
void mergeSort(vector<int>&arr, int low, int high) {
	if (low < high) {
		//中间点mid
		int mid = low + (high - low) / 2;

		//递归分开数组
		mergeSort(arr, low, mid);   //左子数组
		mergeSort(arr, mid+1, high);//右子数组

		//合并数组
		merge(arr, low, mid, high);
	}
}
int main() {
	vector<int> arr = { 12, 11, 13, 5, 6, 7 };
	mergeSort(arr, 0, arr.size() - 1);

	cout << "Sorted array: ";
	for (int num : arr) {
		cout << num << " ";
	}
	cout << endl;

	return 0;
}

2.为什莫分别对左右子数组排序完之后还要拷贝剩余的元素？

//拷贝L的剩余元素
while (i < left) {
	arr[k] = L[i];
	i++;
	k++;
}//拷贝R的剩余元素
while (j < right) {
	arr[k] = R[j];
	j++;
	k++;
}

在归并排序的合并过程中，剩余元素的情况发生在两个已排序的子数组L和R不完全相同长度时。这是因为归并排序的工作原理是将数组分成两半，递归地对它们进行排序，然后将它们合并在一起。以下是一些可能导致剩余元素的情况：

1. 不完全对半分：当原始数组长度为奇数时，在递归分解过程中，某个层的子数组不会完全对半分。这意味着一个子数组将比另一个子数组多一个元素。在合并这些子数组时，较短的那个子数组会先被完全合并，而较长的子数组将有一个剩余元素。

2. 递归基：递归的最底层是只包含一个元素的子数组。这些子数组被视为已排序的，在合并过程中，它们会被直接放入合并后的数组中，而不需要比较。

3. 合并过程中的比较：在合并过程中，我们比较L和R中的元素，并将较小的元素放入arr中。如果L中的所有元素都小于R中的元素，那么在将L中的所有元素放入arr之后，R中可能还有剩余元素。反之亦然，如果R中的所有元素都小于L中的元素，那么在将R中的所有元素放入arr之后，L中可能还有剩余元素。

在merge函数中，处理剩余元素的代码是为了确保所有元素都被正确地合并到最终的排序数组中。当其中一个子数组的元素全部被合并后，另一个子数组中可能还有未被合并的元素，这些剩余元素会被依次拷贝到原数组arr的剩余位置上。