基于多尺度小波变换的信号峰值检测算法（Python）

详细流程图

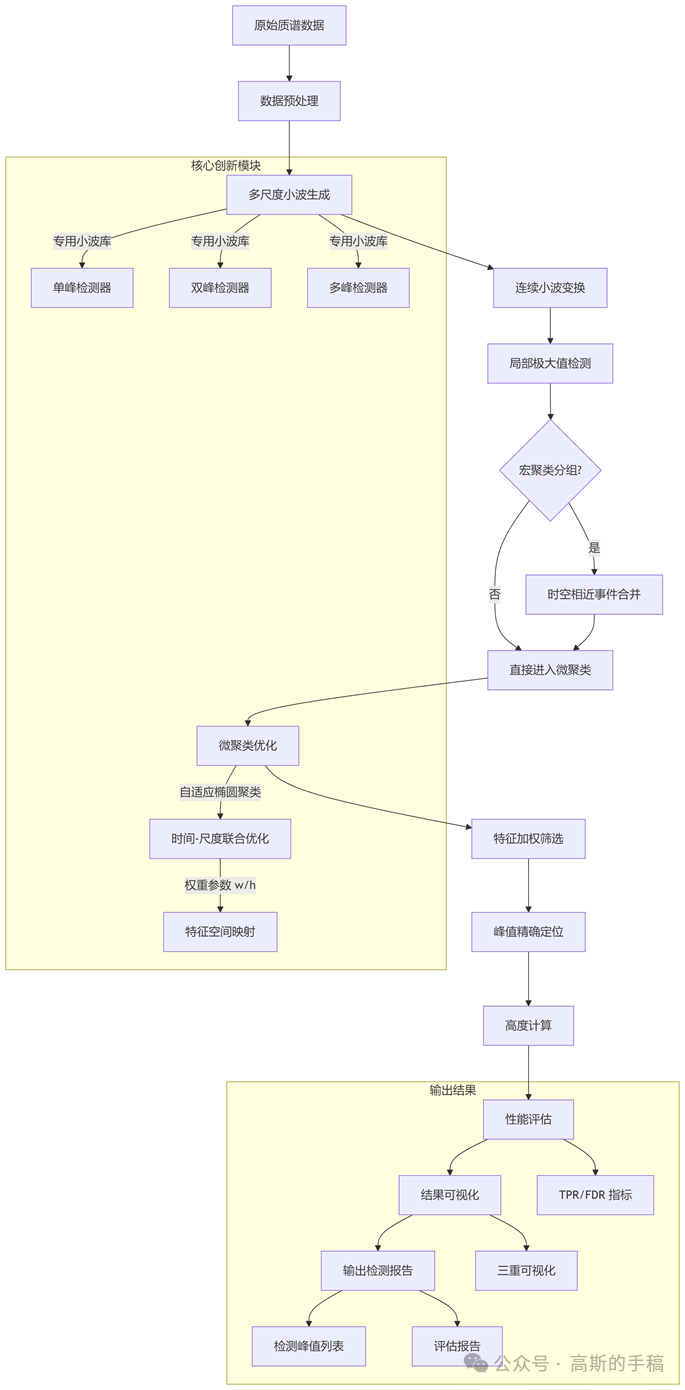
流程说明：

1.数据输入：读取原始质谱数据（含噪声）和真实峰值标注

2.小波制备：动态生成针对不同峰形的检测小波

3.特征提取：

通过连续小波变换提取多尺度特征

检测各尺度上的局部极大值点

4.聚类优化：

宏聚类：合并时空相近的候选点（减少冗余）

微聚类：在特征空间中精选最优峰值（w/h参数控制精度）

5.精确定位：在检测位置附近窗口内确定真实峰值

6.评估输出：

计算TPR（真阳性率）和FDR（假发现率）

生成三重可视化：信号图+标记图+小波热力图

创新点

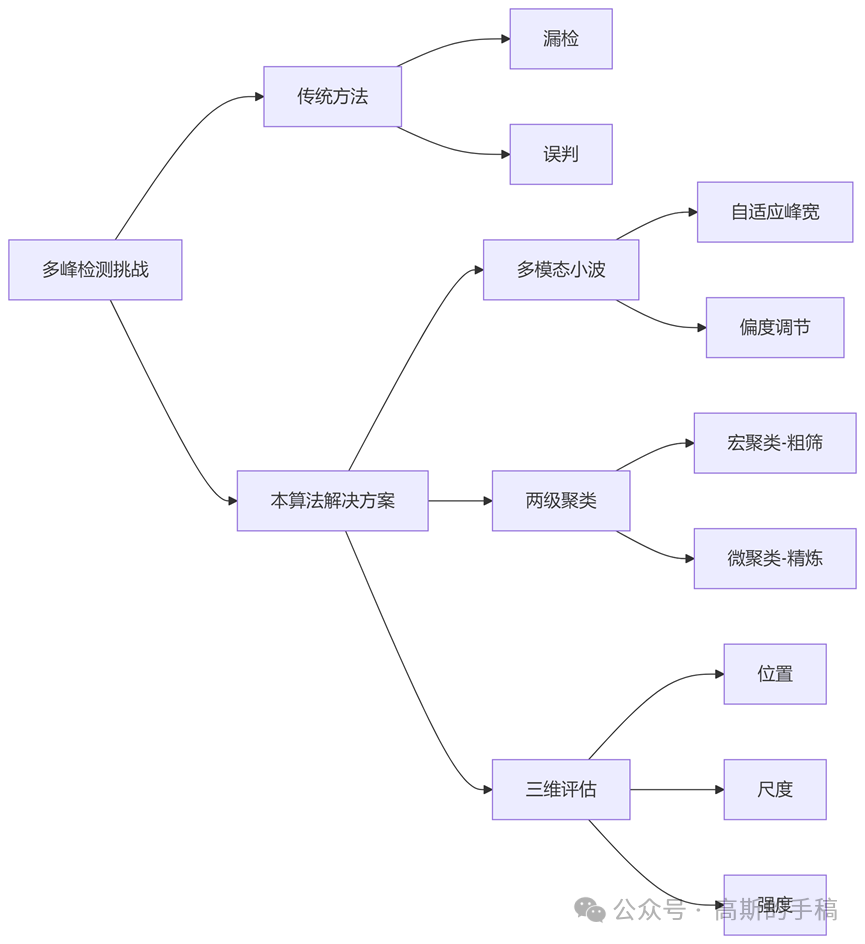
部分代码如下：

def cwt_local_maxima(trace,scales,events_scales,wavelets,wavelet_args,threshold,macro_clusters=True,show_wavelets=False,extent=1):
    """ 
    集成CWT计算和局部极大值检测

    参数:
    trace : array_like
        输入信号数组
    scales : array_like
        尺度值数组
    events_scales : array_like
        布尔数组，指示哪些尺度用于事件检测
    wavelets : list of str
        小波函数名称列表
    wavelet_args : list
        每个小波的参数列表
    threshold : float
        局部极大值检测的阈值
    macro_clusters : bool
        使用宏聚类（默认True）
    show_wavelets : bool
        显示小波函数（默认False）
    extent : float
        事件合并的距离扩展因子（默认1）

    返回:
    local maxima : list of ndarray
        局部极大值事件数组列表
    """
    # 初始化事件数组
    all_events = np.empty((0,), dtype=d_type)
    wvlts = {wavelet:{} for wavelet in wavelets}
    if show_wavelets:
        plt.figure()
    class_n = 0

    # 遍历所有小波类型
    for wavelet,wavelet_args in zip(wavelets,wavelet_args):
        # 生成小波函数
        if wavelet == 'ricker': 
            N = 1 
            wvlts[wavelet] = {'N':N, 'w':[ricker(s) for s in scales]}
        elif wavelet[:4] == 'msg-':
            N = int(wavelet[4:]) 
            if wavelet_args == None:
                wvlts[wavelet] = {'N':N, 'w':[msg(s, N=N, mod=0.8, shift=1, skewness=0.5) for s in scales]} 
            else:
                wvlts[wavelet] = {'N':N, 'w':[msg(s, N=N, **wavelet_args) for s in scales]} 
        elif wavelet[:5] == 'msge-':
            N = len(wavelet[5:]) 
            if wavelet_args == None:
                wvlts[wavelet] = {'N':N, 'w':[msg_encoded(s, pattern=wavelet[5:], mod=1.5, shift=-2.9, skewness=0.04) for s in scales]}
            else:
                wvlts[wavelet] = {'N':N, 'w':[msg_encoded(s, pattern=wavelet[5:], **wavelet_args) for s in scales]}
        elif wavelet[:7] == 'morlet-':
            N = int(wavelet[7:]) 
            wvlts[wavelet] = {'N':N, 'w':[morlet(s, N=N, is_complex=False) for s in scales]}
        elif wavelet[:8] == 'cmorlet-':
            N = int(wavelet[8:])
            wvlts[wavelet] = {'N':N, 'w':[morlet(s, N=N, is_complex=True) for s in scales]}

        # 显示小波函数
        if show_wavelets:
            plt.plot(wvlts[wavelet]['w'][0],label=wavelet)

        # 复小波处理
        if np.iscomplexobj(wvlts[wavelet]['w'][0]):
            for n, w in enumerate(wvlts[wavelet]['w']):
                # 计算卷积的有效区域
                _l = floor(min(len(trace),len(w))/2)
                # 计算卷积并取模
                _cwt = np.abs(convolve(trace, w, mode='valid'))
                # 检查当前尺度是否用于事件检测
                if events_scales[n]:
                    # 查找局部极大值
                    _index, _ = find_peaks(_cwt, distance=wvlts[wavelet]['N']*scales[n], height=threshold)
                    # 添加事件到数组
                    all_events = np.append(all_events, np.array(list(zip((_index+_l), [scales[n]]*len(_index), _cwt[_index], [0]*len(_index), [wvlts[wavelet]['N']]*len(_index), [class_n]*len(_index))), dtype=d_type), axis=0)
        # 实小波处理
        else:
            for n, w in enumerate(wvlts[wavelet]['w']):
                _l = floor(min(len(trace),len(w))/2)
                # 计算卷积
                _cwt = (0.5*convolve(trace, w, mode='valid')) 
                _cwt += np.abs(_cwt)
                if events_scales[n]:
                    _index, _ = find_peaks(_cwt, distance=wvlts[wavelet]['N']*scales[n], height=threshold)
                    all_events = np.append(all_events, np.array(list(zip((_index+_l), [scales[n]]*len(_index), _cwt[_index], [0]*len(_index), [wvlts[wavelet]['N']]*len(_index), [class_n]*len(_index))), dtype=d_type), axis=0)
        class_n += 1

    # 显示小波函数
    if show_wavelets:
        plt.legend()
        plt.show()

    # 执行宏聚类
    if macro_clusters:
        # 计算事件左边界
        all_events_t_l = all_events['loc']-0.5*extent*np.multiply(all_events['N'],all_events['scale']) 
        # 按左边界排序
        _index_l = np.argsort(all_events_t_l) 
        # 计算事件右边界
        all_events_t_r = all_events['loc']+0.5*extent*np.multiply(all_events['N'],all_events['scale']) 
        # 按右边界排序
        _index_r = np.argsort(all_events_t_r) 
        # 计算事件重叠
        all_events_overlap = all_events_t_r[_index_r[:-1]]-all_events_t_l[_index_l[1:]] 
        # 找到分割点
        _slices = np.argwhere(all_events_overlap <= 0).flatten()+1 
        # 分割事件数组
        _mc = np.split(all_events[_index_l], _slices, axis=0) 
        return _mc
    else:
        return [all_events]

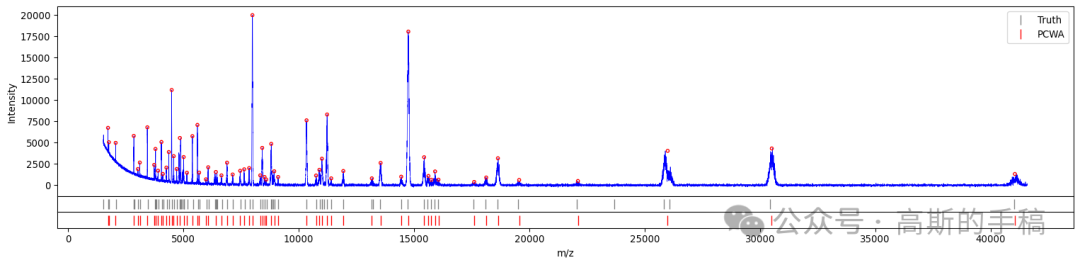
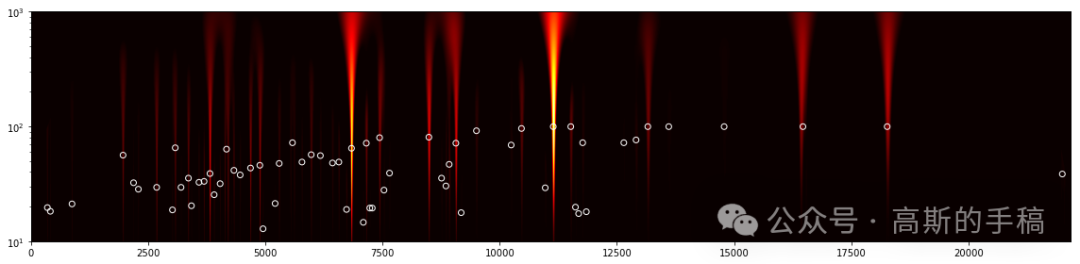
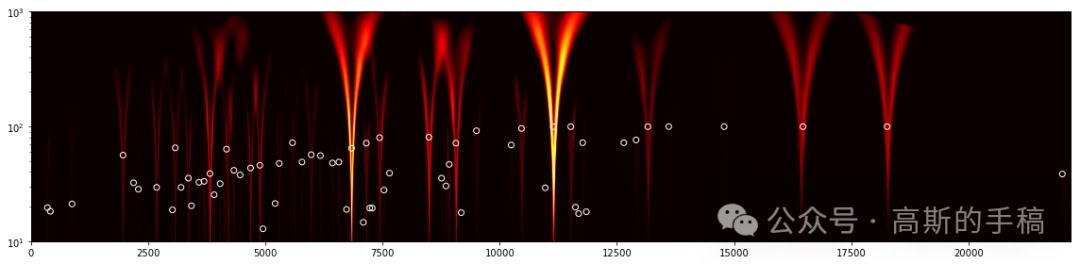
完整数据和详细注释代码通过知乎学术咨询获得(哥廷根数学学派)：