算法训练篇04--力扣11.盛水最多的容器

目录

1.题目链接：11.盛最多水的容器

2.题目描述：

3.解法

4.C++算法代码：

---

1.题目链接：11.盛最多水的容器

2.题目描述：
 

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

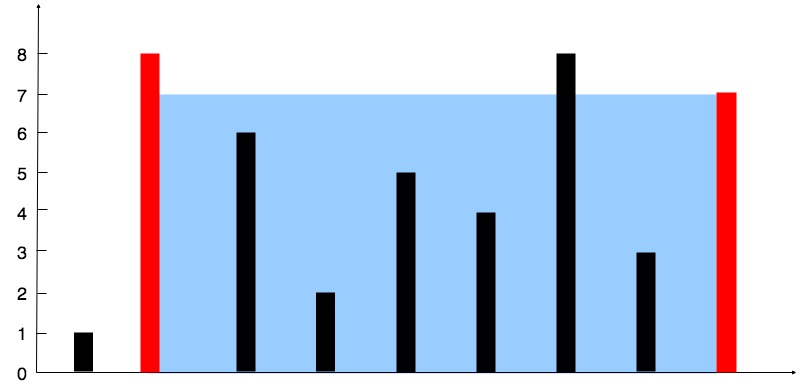
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

3.解法

解法一(暴力求解)：计算出所有容器的体积，然后找出其中容积最大的值。

缺点：会超时

解法二(对撞指针)：

算法思路：

设两个指针left，right分别指向容器的左右两个端点，此时容器的容积：

v = （right - left）*min(height(left), height(right))

容器左边界为height[left], 右边界height[right]

为了方便叙述，我们假设左边边界小于右边边界。

如果此时我们固定一个边界，改变另一个边界，水的容积会有如下变化形式：

• 容器的宽度一定变小
• 由于左边界小，决定了水的高度。如果改变左边界，新的水面高度不确定，但是一定不会超过右边的柱子的高度，因此容器的容积可能会增大。
• 如果改变右边界，无论右边界移动到哪里，新的水面的盖度一定不会超过左边界，也就是不会超过现在的水面高度，但是由于容器的宽度减小，因此容器的容积一定会变小的。

由此可见，左边界和其余边界的组合情况都可以不用考虑。所以我们可以left++替换这个边界，继续判断下一个左右边界。

当我们不断重复上述过程，每次都可以舍去大量不必要的枚举过程，直到left与right相遇。期间产生的所有容积里面的最大值，就是最终的答案。

4.C++算法代码：

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0,right = height.size()-1,ret = 0;
        while(left<right)
        {
            int v = min(height[left],height[right])*(right-left);
            ret = max(ret,v);
            height[left] > height[right]?right--:left++;

        }
        return ret;
    }
};