【基础算法总结】队列+宽搜篇

一，算法介绍

与栈类似，队列也是一种基础的，并且常用的存储数据的容器，它有先进先出的特性。
纯队列的算法题比较少，队列这种数据结构一般用于服务宽搜算法(宽度优先遍历/层序遍历/bfs算法)。

bfs算法的应用十分广泛，比如树结构中的应用，图论中的应用，最短路问题，迷宫问题，拓扑排序问题等都可用bfs解决。本篇文章选取的题目都是bfs算法在树结构中的应用。

二，算法原理和代码实现

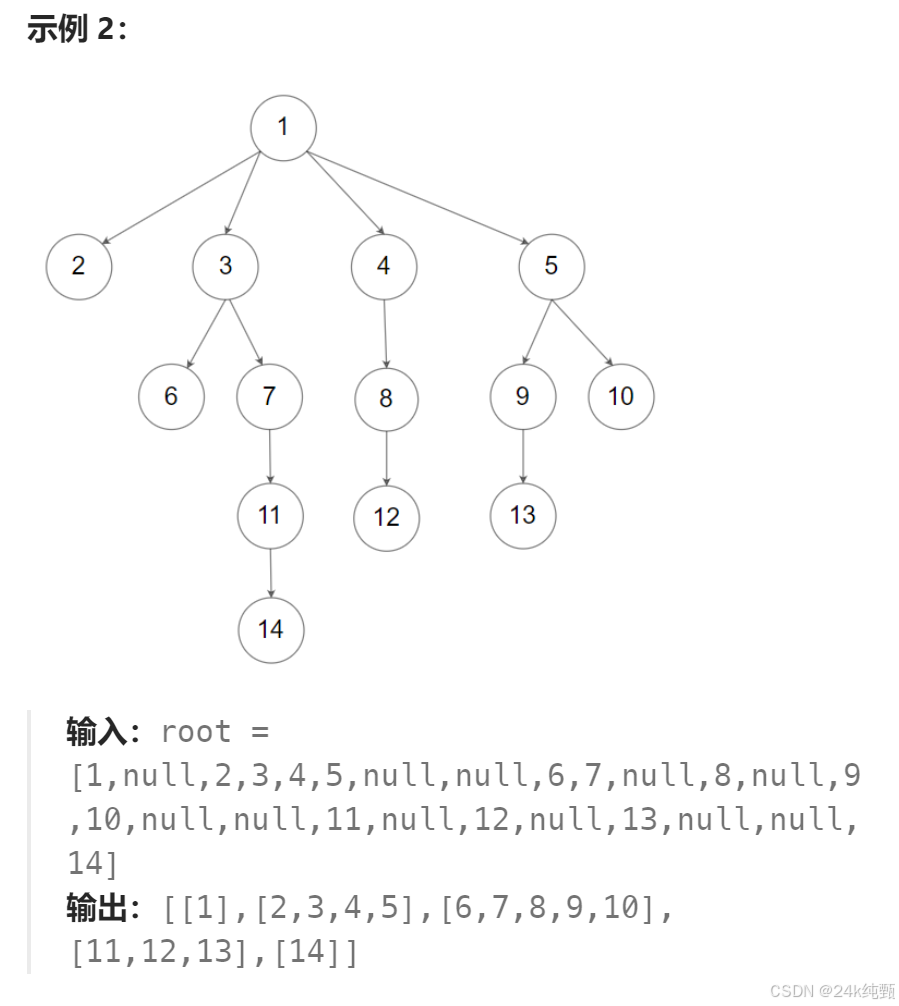
429.N叉树的层序遍历

算法原理：

本题是一道纯粹的层序遍历，类似于一个模版题。在前面已经学习了二叉树的层序遍历，就是在每次出节点的同时把左右子节点入队列即可。本题不同的点是N叉树，所以需要多加⼀个变量，⽤来记录每⼀层结点的个数 sz 就好了，每次出节点的同时要使用循环把下一层的节点入队列。

代码实现：

class Solution 
{
public:
    vector<vector<int>> levelOrder(Node* root) 
    {
        vector<vector<int>> ret; // 返回结果
        queue<Node*> q;

        // 处理特使情况
        if(root == nullptr) return ret;
        
        q.push(root);
        while(q.size())
        {
            int sz = q.size(); // 先求出本层元素的个数
            vector<int> tmp; // 记录这一层的节点
            for(int i = 0; i < sz; i++) 
            {
                Node* t = q.front();
                q.pop();
                tmp.push_back(t->val);

                // 把下一层的节点入队列
                for(Node* child : t->children)
                    q.push(child);
            }
            ret.push_back(tmp);
        }
        return ret;
    }
};

103.二叉树的锯齿形层序遍历

算法原理：

本题是上一题的简单变式题，思路和代码实现基本和上一题的一模一样。
唯一不同的是需要增加一个标记，记录偶数层，当层数为偶数时，只需把这一层的元素序列逆序即可。

代码实现：

class Solution 
{
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) 
    {
        vector<vector<int>> ret;
        queue<TreeNode* > q;

        if(root == nullptr) return ret;
        q.push(root);
        int cnt = 0;
        while(q.size())
        {
            int sz = q.size(); // 计算本层节点数
            vector<int> tmp;
            for(int i = 0; i < sz; i++)
            {
                TreeNode* t = q.front();
                q.pop();
                tmp.push_back(t->val);

                // 入左右节点
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
            cnt++;
            // 是偶数层，就逆序
            if(cnt % 2 == 0) reverse(tmp.begin(), tmp.end());
            ret.push_back(tmp);
        }
        return ret;
    }
};

662.二叉树最大宽度

算法原理：

解法：利用数组存储二叉树的方式，给节点编号。
使用队列，里面存pair类型，把每个节点和它的编号绑在一起，设计编号根节点从1开始，用类似堆中数组存储二叉树的方式，左孩子的下标计算公式为 2x，右孩子下标计算公式为 2x+1。
每层节点入完后，就更新最大宽度，只要用每层的队头与队尾元素的下标相减 +1 即可。

细节问题：

(1) 可用数组模拟队列，方便取队头和队尾元素。
(2)下标有可能溢出。如果二叉树层数很深，下标有可能超出 int 范围。但是当我们相减之后，即使溢出，结果也是正确的。回想一下数据的环形存储，即使溢出了，相减求的是距离，距离是不会溢出的。
(3) 在C++中，溢出会报错，为了防止报错，我们用无符号整型存下标。
(4) 用数组模拟队列会有另一个问题，就是原来在使用队列时经常有头删的操作，但是数组的头删时间复杂度是O(N)，如果直接在数组上操作，会导致效率太低，所以在接收下一层的节点时要再创建一个临时数组，把下一层的节点存好后直接覆盖原来的数组。

代码实现：

class Solution 
{
public:
    int widthOfBinaryTree(TreeNode* root) 
    {
        vector<pair<TreeNode*, unsigned int>> q; // 用数组模拟队列
        q.push_back({root, 1});
        unsigned int ret = 0;

        while(q.size())
        {
            // 用每层的队头队尾元素更新宽度
            auto& [x1, y1] = q[0];
            auto& [x2, y2] = q.back();
            ret = max(ret, y2 - y1 + 1);

            // 入下一层的左右子树
            vector<pair<TreeNode*, unsigned int>> tmp;
            for(auto& [x, y] : q)
            {
                if(x->left) tmp.push_back({x->left, 2 * y});
                if(x->right) tmp.push_back({x->right, 2 * y + 1});
            }
            q = tmp; // 覆盖原数组
        }

        return ret;
    }
};

515.在每个树行中找最大值

算法原理：

本题也是层序遍历的变式题，只要在每一层入队列时，定义一个变量统计出最大值即可。

代码实现：

class Solution 
{
public:
    vector<int> largestValues(TreeNode* root) 
    {
        vector<int> ret;
        queue<TreeNode*> q;

        if(root == nullptr) return ret;
        q.push(root);
        
        while(q.size())
        {
            int sz = q.size();
            int tmp = INT_MIN;
            for(int i = 0; i < sz; i++)
            {
                TreeNode* t = q.front();
                q.pop();
                tmp = max(tmp, t->val);
                
                // 左右子树入队列并且统计出最大值
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
            }
            ret.push_back(tmp);
        }
        return ret;
    }
};

在找最大值时还可以使用容器进行排序：

三，算法总结

通过上面若干道题目可知，使用队列实现宽搜算法的代码是有大致模版的，其核心代码基本一样。