初阶C语言：函数的嵌套、链式访问、递归、迭代

本文链接：https://blog.youkuaiyun.com/2301_77736034/article/details/144901102

1. 函数的嵌套调用

函数可以嵌套调用，不可以嵌套定义

#include<stdio.h>
void print()
{
    printf("hehehehe\n");
}
void three_print()
{
    int i = 1;
    for(i = 0;i <= 3;i++)
    {
        print();    
    }
}
int main()
{
    three_print();
    return 0;
}

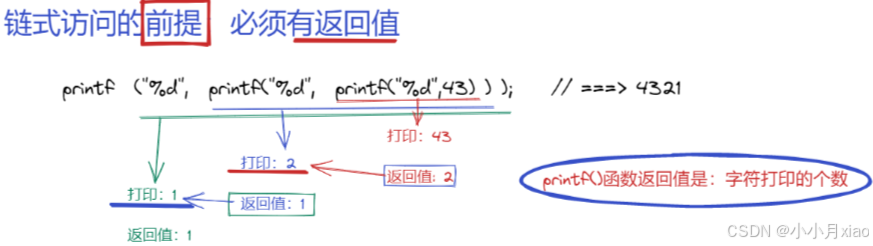
2. 链式访问

将一个函数的返回值作为另一个函数的参数

#include <stdio.h>
#include <string.h>
int main()
{
    // 普通访问
    int len = strlen("abcdefg");
    printf("%d\n",len);
    
    // 链式访问（将函数串起来）
    printf("%d\n",strlen("abcdefg"));
}

3. 函数的递归：程序调用自身的编程技巧

（1）递归的定义

递归是一种常用的程序算法，一个程序或函数在其定义或说明中直接或间接调用自身的一种方法
通常，把一个大型的复杂问题层层转化为一个与原问题相似的、规模较小的问题求解 —— 递归策略
作用：只需少量的代码就可以描述出接替过程中需要的多次重复计算，大大减少了程序的代码量

（2）核心：大事化小

例如：接收一个整型值（无符号），按照顺序打印它的每一位

#include <stdio.h>
void print(int n)
{
    if(n > 9)
    {
        print(n / 10);            
    }
    printf("%u  ",n % 10); 
}
int main()
{
    unsigned num = 1234;
    printf("请输入整数：");
    scanf("&u",&num);
    print(num);
    return 0;
}

（3）递归的必要条件

存在限制条件，当满足这个限制，递归便不再继续
每次递归之后，越来越接近这个限制条件

（4）例题：编写函数允许创建临时变量时，求字符串长度

#include<stdio.h>
//int my_strlen(char str[])    //参数部分写成数组形式
int my_strlen(char* str)    //参数部分写成指针形式
{
    int count = 0;    // 临时变量
    while(*str != '\0')
    {
         count++;
         str++;    //找些一个字符，指针++       
    }    
}
int main()
{
    //int len = my_strlen("abc");    // 实参传给函数形参的时首字符的 地址，相当于如下：
    char arr[] = "abc";    // [a ,b, c, \0]
    int len = my_strlen(arr);    // 传给函数形参的是 一个字符的地址，所以函数参数为 char*
    printf("%d",len);
    return 0;
}

（5）例题：编写函数不允许创建临时变量时，求字符串长度

#include<stdio.h>
int my_strlen(char* str)
{
    if(*str != '\0')
    {
         return 1 + my_strlen(str+1);    //str++ : 前置，先使用后++ ————> 会导致死递归；  ++str : 最终值一样，但会导致 str的值变化     
    }
    else
    {
        return 0;    
    }
}
int main()
{
    //int len = my_strlen("abc");    // 实参传给函数形参的时首字符的 地址，相当于如下：
    //char arr[] = "abc";
    int len = my_strlen(arr);
    printf("%d",len);
    return 0;
}

4. 迭代

在 C 语言中，迭代通常通过循环结构来实现。主要的循环结构有for循环、while循环和do - while循环。

（1）迭代在 C 语言函数中的应用

可以将迭代过程封装在函数中。例如，编写一个函数来计算一个数的阶乘。

#include <stdio.h>
int factorial(int n)
{
    int result = 1;
    for(int i = 1; i <= n; i++)
    {
        result *= i;
    }
    return result;
}
int main()
{
    int n = 5;
    int fact = factorial(n);
    printf("%d的阶乘为：%d\n", n, fact);
    return 0;
}

5. 递归与迭代

（1）练习1：求 n 的阶乘（不考虑溢出）

递归实现

#include<stdio.h>
int fac(int n)                                // 5! = 5*4! 
{                                        // 4！= 4*3！
    if(n<=1)                             // 3！= 3*2！
        return 1;                        // 2！= 2*1！
    else                                 // 1! = 1  此时 n=1；,递延完成
        return n*fac(n-1);    
}
int main()
{
    int n = 0;
    scanf("%d",&n);
    int ret = fac(n);
    printf("ret = %d\n",ret);
    return 0;
}

迭代实现（非递归）

int fac(int n)                                 
{                                        
    int i = 0;
    int ret = 1;
    for(i = 1;i <= n; i++)
    {
        ret = ret * i;    
    }   
    return ret;
}
int main()
{
    int n = 0;
    scanf("%d",&n);
    int ret = fac(n);
    printf("ret = %d\n",ret);
    return 0;
}

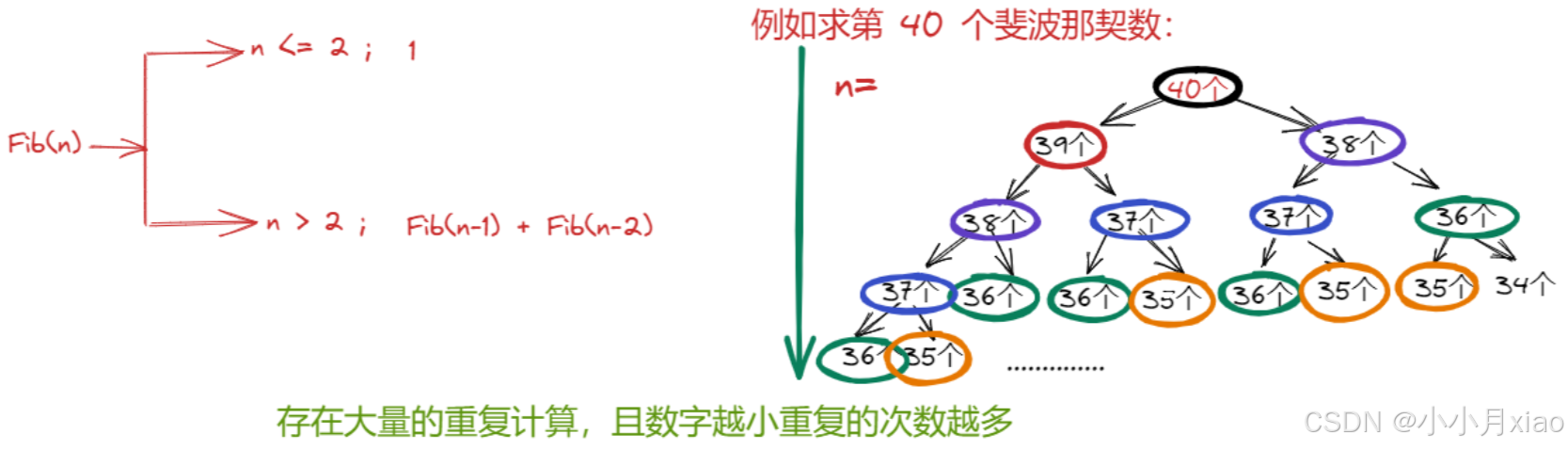
（2）练习2：求第n个斐波那契数

递归实现

#include<stdio.h>
int count = 0;
int Fib(int n)
{
    if(n = 5)
    {
        count++ ;   
    }
    if(n <= 2)
        return 1;
    else
        return Fib(n-2) + Fib(n-1);
}
int main() 
{
    int n = 0;
    scanf("%d",&n);
    int ret = Fib(n);
    printf("%d\n", ret);
    printf("%d",count);
    return 0;
}

迭代实现

#include<stdio.h>
int fib(int n)
{
    int a = 1, b = 1;
    int c = 1;
    while(n >= 3)
    {
        c = a + b;
        a = b;
        b = c; 
        n--; 
    }
    return c;
}
int main()
{
    int n = 1;
    scanf("%d",&n);
    int ret = fib(n);
    printf("%d\n",ret);
    return 0;
}

#include<stdio.h>
int fib(int n)
{
    int a = 1, b = 1;
    int c = 1;
    for(int i = 1; i <= n-2; i++)
    {
        c = a + b;
        a = b;
        b = c;    
    }
    return c;
}
int main()
{
    int n = 1;
    scanf("%d",&n);
    int ret = fib(n);
    printf("%d\n",ret);
    return 0;
}

6. 总结

许多题目可以使用都会进行解释，这是因为递归比非递归的显示更清晰，但是这些问题的的迭代实现可能往往比递归实现效率更高（虽然代码可读性稍微差一点），当一个问题相当复杂，无法使用迭代实习时，此时使用递归实现的简洁性以补偿它所带来的允许时的开销

7. 函数递归经典问题

（1）汉诺塔问题

是一个经典的递归和迭代问题。它由三根柱子（通常标记为 A、B、C）和若干个大小不同的圆盘组成。初始时，所有圆盘按照从大到小的顺序堆叠在一根柱子（比如 A 柱）上。

#include<stdio.h>
void move(char f, char t)
{
    printf("%c --> %c\n", f, t);
}
void fn_num(int n, char A, char B, char C)
{
    if (n == 1)
        move(A, C);
    else
    {
        fn_num(n - 1, A, C, B);
        move(A, C);
        fn_num(n - 1, B, A, C);
    }
}
int main()
{
    int n = 0;
    char a = 'A', b = 'B', c = 'C';
    printf("请输入塔盘数：");
    scanf("%d", &n);
    fn_num(n, a, b, c);
    return 0;
}

（2）青蛙跳台阶问题

有一只青蛙要跳上 n 级台阶，青蛙每次可以跳 1 级台阶，也可以跳 2 级台阶，问青蛙跳上 n 级台阶总共有多少种不同的跳法。

#include<stdio.h>
int fb(int n)
{
	if (n == 1)
		return 1;
	else if (n == 2)
		return 2;
	return fb(n - 1) + fb(n - 2);
}
int main()
{
	int n = 0;
	printf("一共有多少个台阶：");
	scanf("%d", &n);
	int sum = fb(n);
	printf("%d", sum);
	return 0;
}