1、什么是边界值测试用例设计法?
边界值测试是从输入域测试中衍生出来的。边界的条件落在等价类的边界上、边界外和边界内,边界值测试是对等价类测试的一个补充,但不同于等价类测试。由长期测试工作经验得知,大量的错误是发生在输入域或输出域的边界上,因此针对各种边界情况设计测试用例,可以查出更多的错误。
边界值分析方法的理论基础是假定大多数的错误是发生在各种输入条件的边界上,如果在边界附近的取值不会导致程序出错,那么其他取值导致程序出错的概率会很小。
2、边界值的相关定义
上点:就是边界上的点,如果该域的边界是封闭的,上点就在域范围内;如果域的边界是开放的,上点就在域范围外。
离点:就是离上点最近的一个点,如果域的边界是封闭的,离点就在域范围外;如果域的边界是开放的,离点就在域范围内。
内点:顾名思义,就是在域范围内的任意一个点。
上点和离点的确定与该域的边界是开放的还是封闭的有关,但不论边界是开放的还是封闭的,上点和离点总是一个在域内,另一个在域外。如对于封闭边界,上点在域内,离点在域外;对于开放边界,上点在域外,离点在域内。例如,假设A 是整数,A 的边界描述为A>0,那么上点为0,离点为1;如果边界描述为A=0,那么上点仍然为0,但离点为-1。
上点和离点的选择还与区间的数据类型有关,对于整数,离点可以通过在上点的基础上加1或减1 来确定;对于实数,可以选择一个精度,在该精度下寻找最靠近的离点。例如,假设A 是实数,首先需要确定精度,若精度为0.001,如果A 的边界描述为A>0,那么上点是0,离点为0.001;如果边界描述为A≥0,那么上点仍然为0,但离点为-0.001。
3、边界值与等价类测试方法的区别
等价类划分法可以挑选等价范围内任意一个数据作为代表 边界值分析法要求每个边界值都要作为测试条件
边界值分析法不仅考虑输入条件,同样考虑输出产生的测试情况
4、边界值测试用例设计步骤
分析输入参数的类型:从测试规格中分析得到输入参数类型。
等价类划分:对于输入等价类划分方法进行等价类的划分。
确定边界:运用域测试分析方法确定域范围的边界(上点、离点与内点)。
相关性分析:如果存在多个输入域,则需要运用因果图、判定表方法对这些输入域边界值的组合情况进行进一步分析。
形成测试项:选择这些上点、离点与内点或者这些点的组合形成测试项。
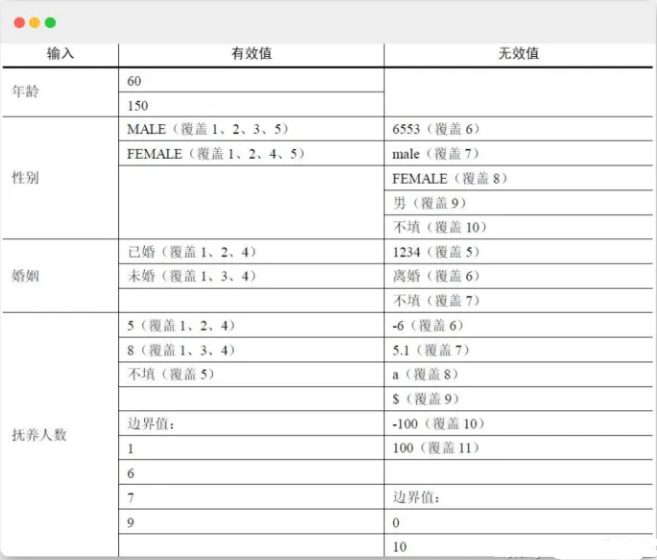
5、边界值测试用例设计案例

最后: 为了回馈铁杆粉丝们,我给大家整理了完整的软件测试视频学习教程,朋友们如果需要可以自行免费领取 【保证100%免费】




























 6924
6924

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








