代码随想录算法训练营第十二天（补） 二叉树| 二叉树理论知识、深度优先遍历、广度优先遍历

目录

一、二叉树理论基础

（一）二叉树的种类

二叉搜索树

平衡二叉搜索树

（二）二叉树的存储

（三）二叉树的遍历

（四）二叉树的定义

二、二叉树的递归遍历

三、二叉树的层序遍历

---

一、二叉树理论基础

代码随想录

（一）二叉树的种类

满二叉树、完全二叉树

满二叉树：如果一棵二叉树只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。

这棵二叉树为满二叉树，也可以说深度为k，有2^k-1个节点的二叉树。

完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。

之前我们刚刚讲过优先级队列其实是一个堆，堆就是一棵完全二叉树，同时保证父子节点的顺序关系。

二叉搜索树

前面介绍的树，都没有数值的，而二叉搜索树是有数值的了，二叉搜索树是一个有序树。

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 它的左、右子树也分别为二叉排序树

下面这两棵树都是搜索树

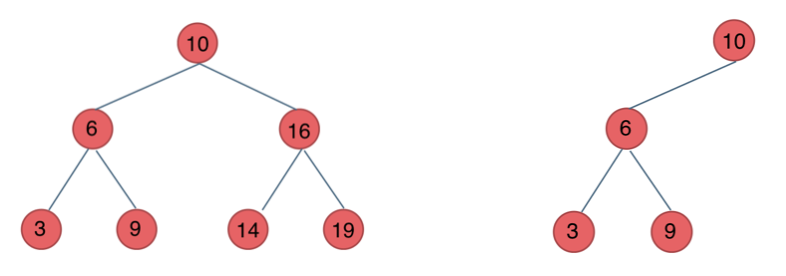
平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

如图：

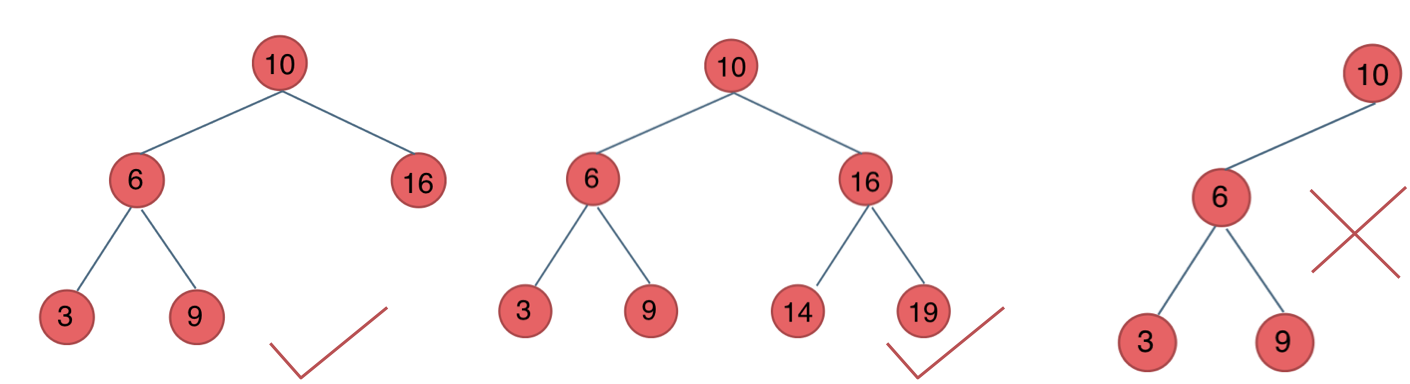
最后一棵 不是平衡二叉树，因为它的左右两个子树的高度差的绝对值超过了1。

C++中map、set、multimap，multiset的底层实现都是平衡二叉搜索树，所以map、set的增删操作时间时间复杂度是logn，注意我这里没有说unordered_map、unordered_set，unordered_map、unordered_set底层实现是哈希表。

所以大家使用自己熟悉的编程语言写算法，一定要知道常用的容器底层都是如何实现的，最基本的就是map、set等等，否则自己写的代码，自己对其性能分析都分析不清楚！

（二）二叉树的存储

二叉树可以链式存储，也可以顺序存储。

那么链式存储方式就用指针， 顺序存储的方式就是用数组。

链式存储如图：

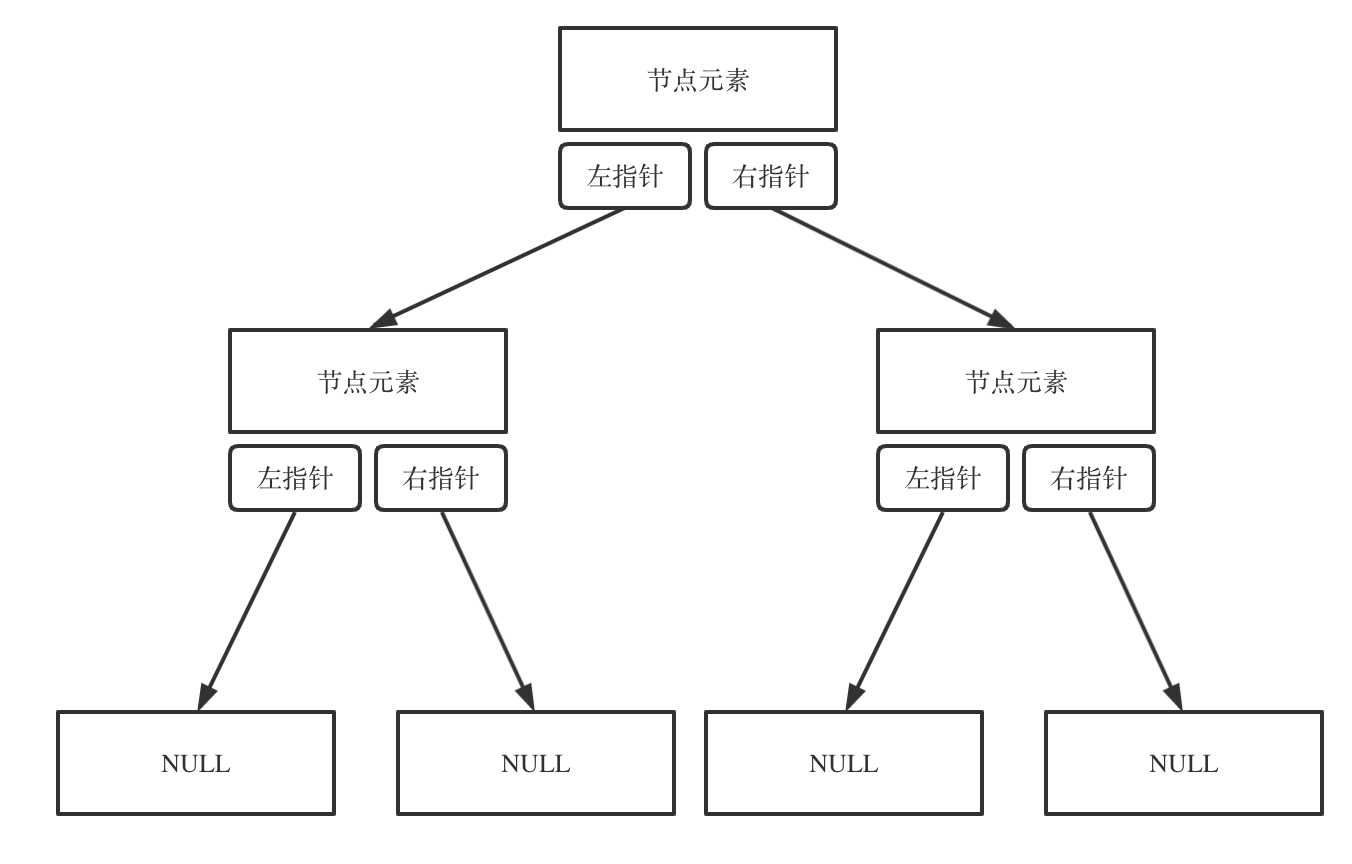
链式存储是大家很熟悉的一种方式，那么我们来看看如何顺序存储呢？

其实就是用数组来存储二叉树，顺序存储的方式如图：

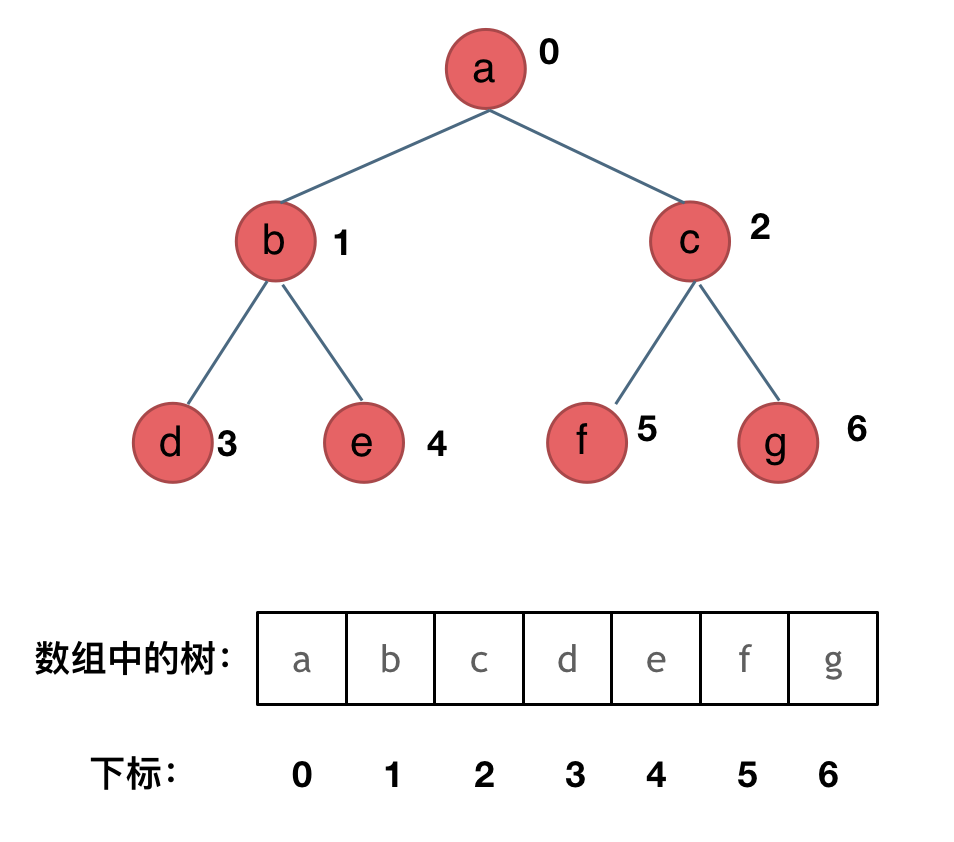
（三）二叉树的遍历

二叉树主要有两种遍历方式：

1. 深度优先遍历：先往深走，遇到叶子节点再往回走。

2. 广度优先遍历：一层一层的去遍历。

深度优先遍历

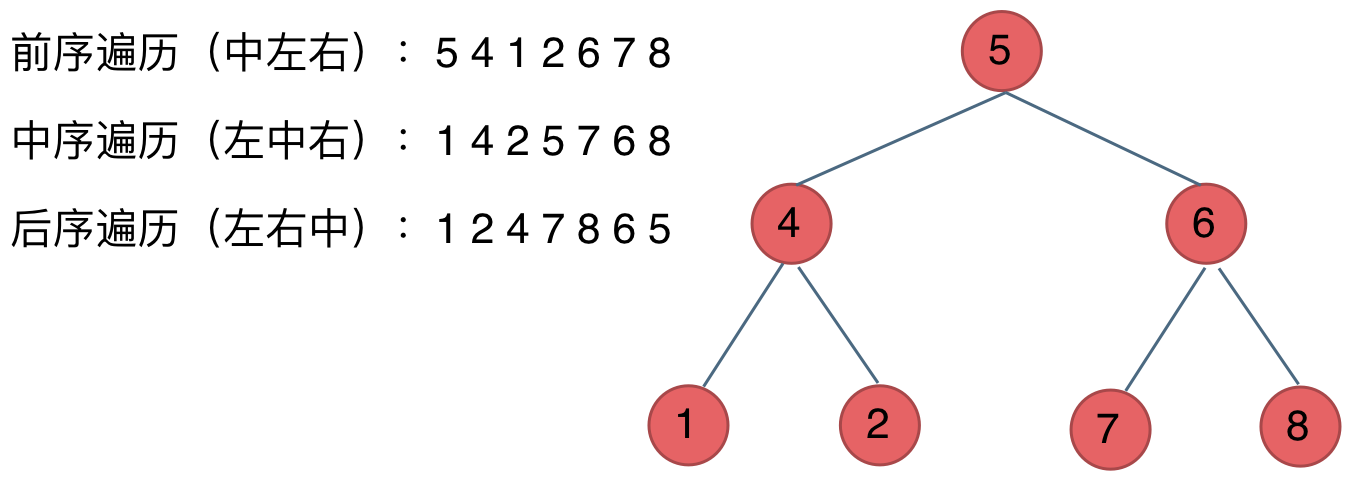
广度优先遍历的实现一般使用队列来实现，这也是队列先进先出的特点所决定的，因为需要先进先出的结构，才能一层一层的来遍历二叉树。

（四）二叉树的定义

C++代码如下：

 struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 };

二、二叉树的递归遍历

《代码随想录》算法视频公开课 (opens new window)：每次写递归都要靠直觉？ 这次带你学透二叉树的递归遍历！ (opens new window)，相信结合视频再看本篇题解，更有助于大家对本题的理解。

大家可以做一做leetcode上三道题目，分别是：

• 144.二叉树的前序遍历(opens new window)

• 145.二叉树的后序遍历(opens new window)

• 94.二叉树的中序遍历

前序遍历

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
 class Solution {
 public:
     void traverse(TreeNode* cur,vector<int>& vec){
         if(cur==NULL) return ;
         vec.push_back(cur->val);
         traverse(cur->left,vec);
         traverse(cur->right,vec);
     }
     vector<int> preorderTraversal(TreeNode* root) {
         vector<int> result;
         traverse(root,result);
         return result;
     }
 };

后序遍历

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
 class Solution {
 public:
     void traverse(TreeNode* cur,vector<int>& cal){
         if(cur==NULL) return ;
         traverse(cur->left,cal);
         traverse(cur->right,cal);
         cal.push_back(cur->val);
     }
     vector<int> postorderTraversal(TreeNode* root) {
         vector<int> arr;
         traverse(root,arr);
         return arr;
     }
 };

中序遍历

 /**
  * Definition for a binary tree node.
  * struct TreeNode {
  *     int val;
  *     TreeNode *left;
  *     TreeNode *right;
  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
  * };
  */
 class Solution {
 public:
     void traverse(TreeNode* cur,vector<int>& cal){
         if(cur==NULL) return;
         traverse(cur->left,cal);
         cal.push_back(cur->val);
         traverse(cur->right,cal);
     }
     vector<int> inorderTraversal(TreeNode* root) {
         vector<int> arr;
         traverse(root,arr);
         return arr;
     }
 };

三、二叉树的层序遍历

力扣题目链接

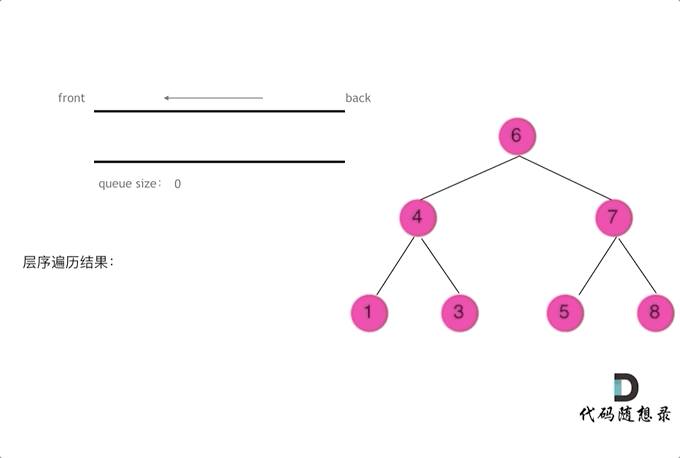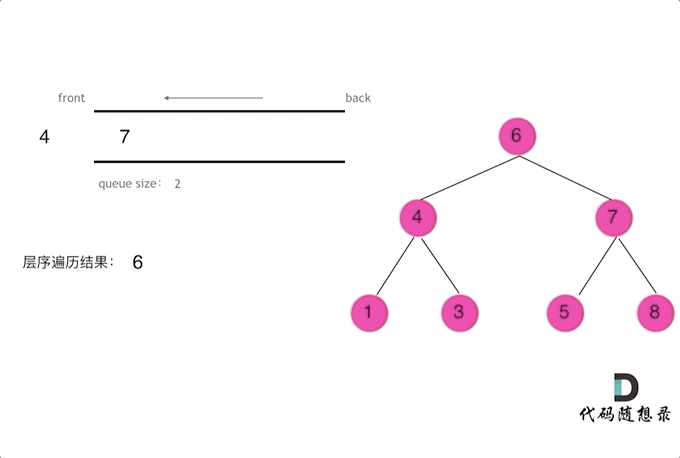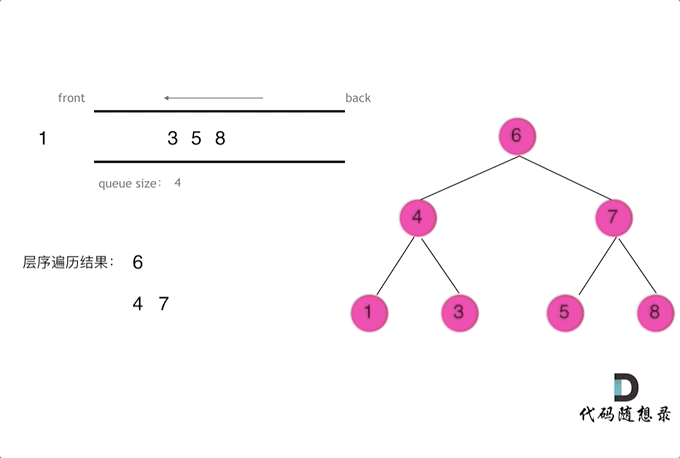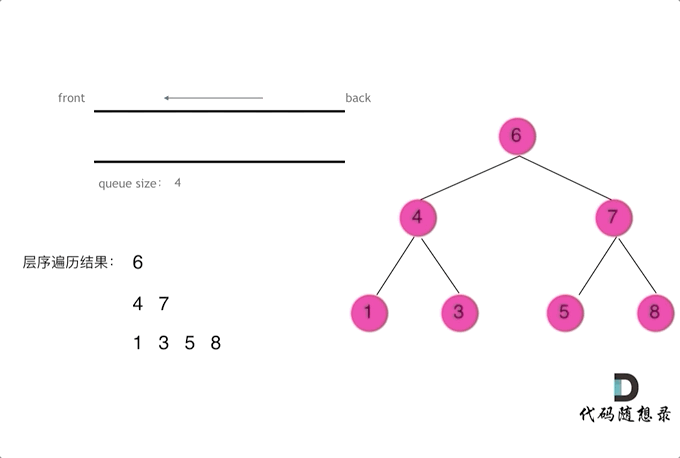
 # 递归法
 class Solution {
 public:
     void order(TreeNode* cur, vector<vector<int>>& result, int depth)
     {
         if (cur == nullptr) return;
         if (result.size() == depth) result.push_back(vector<int>());
         result[depth].push_back(cur->val);
         order(cur->left, result, depth + 1);
         order(cur->right, result, depth + 1);
     }
     vector<vector<int>> levelOrder(TreeNode* root) {
         vector<vector<int>> result;
         int depth = 0;
         order(root, result, depth);
         return result;
     }
 };

 class Solution {
 public:
     vector<vector<int>> levelOrder(TreeNode* root) {
         queue<TreeNode*> que;
         if (root != NULL) que.push(root);
         vector<vector<int>> result;
         while (!que.empty()) {
             int size = que.size();
             vector<int> vec;
             // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
             for (int i = 0; i < size; i++) {
                 TreeNode* node = que.front();
                 que.pop();
                 vec.push_back(node->val);
                 if (node->left) que.push(node->left);
                 if (node->right) que.push(node->right);
             }
             result.push_back(vec);
         }
         return result;
     }
 };

不太理解非递归代码，对于指针以及c++语法不熟悉

今天先学到这里吧，最近事情比较多。