动态规划思想

 动态规划算法思想

 算法的基本思想与分治算法类似，也是将待求解的问题划分为若干子问题，按划分的顺序求解子阶段问题，前一个子问题的解，为后一子问题的求解提供了有用的信息(最优子结构)。在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其它局部解。依次解决各个子问题，最后求出原问题的最优解。
与分治算法最大的区别是: 适合于用动态规划算法求解的问题，经分解后得到的子问题往往不是互相独立的.

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分(即子问题)，再根据子问题的解以得出原问题的解。动态规划往往用于优化递归问题，例如变波那契数列，如果运用递归的方式来求解会重复计算很多相同的子问题，利用动态规划的思想可以减少计算量。
通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，具有天然剪枝的功能，从而减少计算量:一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

动态规划求解问题的基本步骤

 动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。动态规划算法的代码设计都有一定的模式，一般都要经过以下几个步骤:
初始状态 ->决策1 -> 决策2 -> ... -> 决策n > 结束状态

• 1.找出最优解的性质，并刻划其结构特征(找问题状态) 定义dp数组
• 2.递归地定义最优值。(找状态转移方程)
• 3.自底向上的方式计算出最优值
• 4.根据计算最优值时得到的信息，构造最优解.

动态规划算法问题案例

• 硬币选择问题
• 最大子段和
• 最长非降子序列LIS
• 最长公共子序列LCS
• 0-1背包
• 三角数组求和 

 硬币选择问题

 暴力求解方法

 分治算法思想

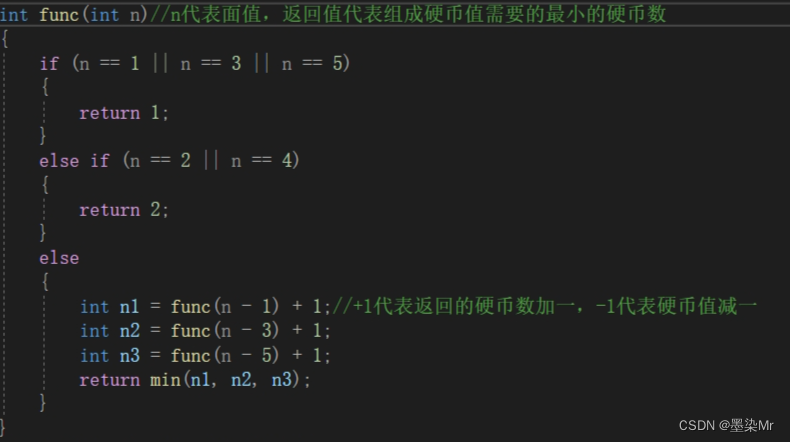
 两个if语句是结束语句，只需要考虑如何结束的最佳状态，当硬币值为1,2,5的时候，只需要一个就可以返回所以返回1，同理，为2,4的时候，只需要2个硬币，所以返回2。

有一个弊端，就是在回溯的时候进行了很多重复的运算，即子问题被重复求解，效率低。

动态分配思想

• 问题的状态(先知道解决最小子问题的状态，然后往上推，推出状态转移方程） : dp[i] 组成面值i所需要的最少的硬币数量
• 状态转移方程(把子问题的最优解合并成原问题的最优解）:dp[0] = 0      dp[1] = 1 + dp[1-1] = 1   
• dp[2] = 1 + dp[2-1] = 1 + dp[1] = 1 + 1 = 2
• dp[3] = 1 + dp[3-1] = 1 + dp[2] = 1 + 2 = 3     选择了3个1分硬币
•          = 1 + dp[3-3] = 1 + dp[] =  1 + 0 = 1      选择了1个3分硬币   1<3  dp[3]=1
• dp[i] = min {1 + dp[i-Vj]}  i表示面值 Vj表示第j个硬币的面额            条件 i>=Vi

非递归的形式来实现动态规划 

暴力for循环 

 

动态规划 

• 状态，即子问题的解
• 状态转移方程，即把子问题合并成原问题的方程 ，可以从最小子问题往上推

 

这里dp[i]存的是第i个元素结尾的最大字段和，原问题是求一整个数组，子问题就可以从两个元素的字段和的最大值开始往上加，最后得到状态转移方程。

代码主体

• 模板就是以XXX结尾的XXX
• 这样可以用小子问题来解决大一级的子问题 
• 找状态的时候要考虑子问题之间是否有关系
• 在字段和问题上，如果上一个子问题的解是负数，就可以直接舍弃，直接用这个这个结尾当做最大值