4985 蜗牛

4985 蜗牛

⭐️难度：中等
⭐️考点：2023、省赛、动态规划
📖

📚

import java.util.*;

public class Main3 {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int[] x = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            x[i] = sc.nextInt();
        }
        int[] a = new int[n + 3];
        int[] b = new int[n + 3];
        for (int i = 1; i < n; i++) {
            a[i] = sc.nextInt();
            b[i + 1] = sc.nextInt();
        }
        double[][] dp = new double[n + 3][2];

        // 动态规划
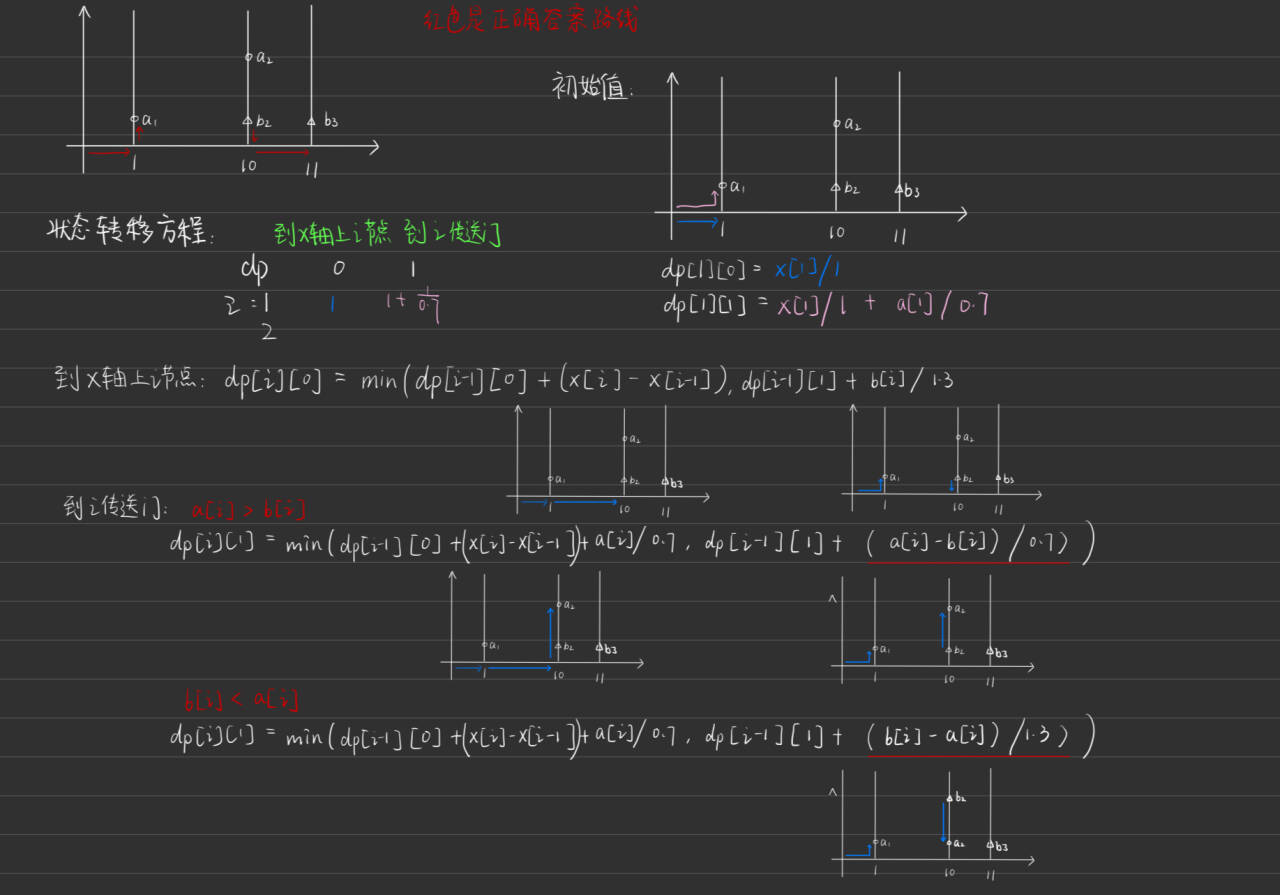
        // 初始值
        dp[1][0] = x[1] / 1;
        dp[1][1] = x[1] / 1 + a[1] / 0.7;
        // 转移方程
        for (int i = 2; i <= n; i++) {
            if(a[i]>b[i]){
                dp[i][1] = Math.min(dp[i-1][0] + (x[i] - x[i-1]) + a[i]/0.7,dp[i-1][1]+(a[i]-b[i])/0.7); // 到下一个传送门 = min（上一个节点 沿x轴走 再往上走，上一个传送门 往上走）
            }else {
                dp[i][1] = Math.min(dp[i-1][0] + x[i] - x[i-1] + a[i]/0.7,dp[i-1][1] + (b[i]-a[i])/1.3);

            }
            dp[i][0] = Math.min(dp[i-1][1]+b[i]/1.3,dp[i-1][0] + x[i] - x[i-1]);  // 到下一个节点 = min（上一个节点 走x轴，上一个传送门 往下走）
        }
        // for (int i = 1; i <= n; i++) {
        //     for (int j = 0; j < 2; j++) {
        //         System.out.print(dp[i][j]+" ");
        //     }
        //     System.out.println();
        // }
        double ans = Math.min(dp[n][0],dp[n][1]);
        System.out.printf("%.2f",ans);
    }
}

题目表述有点不清，我是觉得到达第n根杆就算到达，但是答案有人写的是到达第n根杆的节点算达到，也就是System.out.printf(“%.2f”,a[n][0]);，但两种写法都能过全部案例。

蓝桥调试测试数据：
15
4061 6959 7765 16380 26229 35108 41536 42676 45862 51071 58608 66180 72796 79965 84024
4256 2376 6990 4209 3659 1062 2314 154 3772 1311 4064 4249 3805 4915
2677 4617 276 4097 4656 3911 3966 5520 2685 3704 1084 1825 5598 4510

🍎笔记：