模型比较和变量筛选

最新推荐文章于 2024-08-30 01:00:00 发布
最新推荐文章于 2024-08-30 01:00:00 发布
阅读量1.5k 收藏 19
点赞数 17
分类专栏： R语言学习 文章标签： r语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2301_76815178/article/details/135094555
版权

一、比较两个回归模型

1、ANOVA()比较嵌套模型

如果模型是嵌套关系：

  • Model2 = Model1 + X    （模型一是模型二的一个子集）
  • 我们可以用anova(Model1,Model2)来比较这两个模型
#1.用anova比较嵌套模型
model1 <- lm(TestC ~ Age)
model2 <- lm(TestC ~ Age + TestA + TestB)
anova(model1,model2)

> model1 <- lm(TestC ~ Age)
> model2 <- lm(TestC ~ Age + TestA + TestB)
> anova(model1,model2)
Analysis of Variance Table

Model 1: TestC ~ Age
Model 2: TestC ~ Age + TestA + TestB
  Res.Df    RSS Df Sum of Sq      F  Pr(>F)  
1     98 3123.6                              
2     96 2959.4  2    164.15 2.6623 0.07494 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
  • TestA和TestB是我们想检验的两个模型间是否有差异的部分
  • F = 2.6623 = (164.15/2)/(2959.4/96)
  • 164.15是两个模型残差平方和的差（自由度为所差的变量个数）；2959.4为更为复杂的模型的残差平方和（此例为model2）
  • 此例子中P值并不显著，因此我们不认为加入TestA和TestB后模型有显著的改善

2、AIC()比较非嵌套模型

如果模型不是嵌套关系：

  • Model2 = Model1 +X1 ，Model3 = Model +X2
  • AIC（Model2，Model3），比较Model2和Model3
  • AIC小的模型更优 
    #2、用AIC比较两个非嵌套模型
model2 <- lm(TestC ~ Age + TestA + TestB)
model3 <- lm(TestC ~ Age +relevel(Sex,'Male'))
AIC(model2,model3)
    > model2 <- lm(TestC ~ Age + TestA + TestB)
> model3 <- lm(TestC ~ Age +relevel(Sex,'Male'))
> AIC(model2,model3)
       df      AIC
model2  5 632.5461
model3  4 633.2824
  • 赤池信息准则（Akaike Information Criterion，AIC）
  • AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家赤池弘次在1974年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。
  • 从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型。
  • 一般而言，当模型复杂度提高（k增大）时，似然函数L也会增大，从而使AIC变小，但是k过大时，似然函数增速减缓，导致AIC增大，模型过于复杂容易造成过拟合现象。
  • 目标是选取AIC最小的模型，AIC不仅要提高模型拟合度（极大似然），而且引入了惩罚项，使模型参数尽可能少，有助于降低过拟合的可能性。

二、模型变量选择

1、逐步回归

  • StepAIC(),先给出完整的模型，然后从完整模型中做变量筛选
  • 向前，向后，双向
  • 逐步回归简单易用，但是由很多缺陷
#1、逐步回归法
model.full <- lm(TestC ~ Age + relevel(Sex,"Male") + 
                   relevel(Status,"No disease") + TestA +
                   TestB + Timeinterval_AC + Timeinterval_BC)
summary(model.full)
#向前
model.forward <- stepAIC(model.full,direction = 'forward')
#向后
model.backward <- stepAIC(model.full,direction = 'backward')
#双向
model.both <- stepAIC(model.full,direction = 'both')

 model.full <- lm(TestC ~ Age + relevel(Sex,"Male") + 
+                    relevel(Status,"No disease") + TestA +
+                    TestB + Timeinterval_AC + Timeinterval_BC)
> summary(model.full)

Call:
lm(formula = TestC ~ Age + relevel(Sex, "Male") + relevel(Status, 
    "No disease") + TestA + TestB + Timeinterval_AC + Timeinterval_BC)

Residuals:
    Min      1Q  Median      3Q     Max 
-10.023  -3.490  -1.278   2.018  20.995 

Coefficients:
                                       Estimate Std. Error t value Pr(>|t|)  
(Intercept)                          -1.9345081  2.3524114  -0.822   0.4130  
Age                                   0.1573773  0.0657161   2.395   0.0187 *
relevel(Sex, "Male")Female            1.0035402  1.1837097   0.848   0.3988  
relevel(Status, "No disease")Disease  3.0529009  1.3386101   2.281   0.0249 *
TestA                                 0.0724004  0.0820032   0.883   0.3796  
TestB                                 0.0809508  0.0757371   1.069   0.2879  
Timeinterval_AC                       0.0018494  0.0020716   0.893   0.3743  
Timeinterval_BC                      -0.0002878  0.0020936  -0.137   0.8910  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.48 on 92 degrees of freedom
Multiple R-squared:  0.2866,	Adjusted R-squared:  0.2323 
F-statistic:  5.28 on 7 and 92 DF,  p-value: 4.265e-05

> #向前
> model.forward <- stepAIC(model.full,direction = 'forward')
Start:  AIC=347.89
TestC ~ Age + relevel(Sex, "Male") + relevel(Status, "No disease") + 
    TestA + TestB + Timeinterval_AC + Timeinterval_BC 
#所有变量均进入了模型，没有达到筛选的目的

> #向后
> model.backward <- stepAIC(model.full,direction = 'backward')
Start:  AIC=347.89
TestC ~ Age + relevel(Sex, "Male") + relevel(Status, "No disease") + 
    TestA + TestB + Timeinterval_AC + Timeinterval_BC

                                Df Sum of Sq    RSS    AIC
- Timeinterval_BC                1     0.567 2763.4 345.91
- relevel(Sex, "Male")           1    21.585 2784.4 346.66
- TestA                          1    23.410 2786.3 346.73
- Timeinterval_AC                1    23.936 2786.8 346.75
- TestB                          1    34.308 2797.2 347.12
<none>                                       2762.9 347.89
- relevel(Status, "No disease")  1   156.203 2919.1 351.38
- Age                            1   172.231 2935.1 351.93

Step:  AIC=345.91
TestC ~ Age + relevel(Sex, "Male") + relevel(Status, "No disease") + 
    TestA + TestB + Timeinterval_AC

                                Df Sum of Sq    RSS    AIC
- relevel(Sex, "Male")           1    22.627 2786.1 344.72
- Timeinterval_AC                1    24.175 2787.6 344.78
- TestA                          1    25.450 2788.9 344.82
- TestB                          1    34.805 2798.2 345.16
<none>                                       2763.4 345.91
- relevel(Status, "No disease")  1   158.424 2921.9 349.48
- Age                            1   171.828 2935.3 349.94

Step:  AIC=344.72
TestC ~ Age + relevel(Status, "No disease") + TestA + TestB + 
    Timeinterval_AC

                                Df Sum of Sq    RSS    AIC
- Timeinterval_AC                1    22.706 2808.8 343.53
- TestA                          1    32.560 2818.6 343.88
- TestB                          1    45.415 2831.5 344.34
<none>                                       2786.1 344.72
- relevel(Status, "No disease")  1   173.374 2959.4 348.76
- Age                            1   179.152 2965.2 348.95

Step:  AIC=343.53
TestC ~ Age + relevel(Status, "No disease") + TestA + TestB

                                Df Sum of Sq    RSS    AIC
- TestA                          1    34.031 2842.8 342.74
- TestB                          1    52.725 2861.5 343.39
<none>                                       2808.8 343.53
- relevel(Status, "No disease")  1   150.671 2959.4 346.76
- Age                            1   172.631 2981.4 347.50

Step:  AIC=342.74
TestC ~ Age + relevel(Status, "No disease") + TestB 
#最后是这三个变量纳入了模型中

                                Df Sum of Sq    RSS    AIC
<none>                                       2842.8 342.74
- TestB                          1    73.205 2916.0 343.28
- relevel(Status, "No disease")  1   171.833 3014.6 346.61
- Age                            1   210.514 3053.3 347.88
> #双向
> model.both <- stepAIC(model.full,direction = 'both')
Start:  AIC=347.89
TestC ~ Age + relevel(Sex, "Male") + relevel(Status, "No disease") + 
    TestA + TestB + Timeinterval_AC + Timeinterval_BC

                                Df Sum of Sq    RSS    AIC
- Timeinterval_BC                1     0.567 2763.4 345.91
- relevel(Sex, "Male")           1    21.585 2784.4 346.66
- TestA                          1    23.410 2786.3 346.73
- Timeinterval_AC                1    23.936 2786.8 346.75
- TestB                          1    34.308 2797.2 347.12
<none>                                       2762.9 347.89
- relevel(Status, "No disease")  1   156.203 2919.1 351.38
- Age                            1   172.231 2935.1 351.93

Step:  AIC=345.91
TestC ~ Age + relevel(Sex, "Male") + relevel(Status, "No disease") + 
    TestA + TestB + Timeinterval_AC

                                Df Sum of Sq    RSS    AIC
- relevel(Sex, "Male")           1    22.627 2786.1 344.72
- Timeinterval_AC                1    24.175 2787.6 344.78
- TestA                          1    25.450 2788.9 344.82
- TestB                          1    34.805 2798.2 345.16
<none>                                       2763.4 345.91
+ Timeinterval_BC                1     0.567 2762.9 347.89
- relevel(Status, "No disease")  1   158.424 2921.9 349.48
- Age                            1   171.828 2935.3 349.94

Step:  AIC=344.72
TestC ~ Age + relevel(Status, "No disease") + TestA + TestB + 
    Timeinterval_AC

                                Df Sum of Sq    RSS    AIC
- Timeinterval_AC                1    22.706 2808.8 343.53
- TestA                          1    32.560 2818.6 343.88
- TestB                          1    45.415 2831.5 344.34
<none>                                       2786.1 344.72
+ relevel(Sex, "Male")           1    22.627 2763.4 345.91
+ Timeinterval_BC                1     1.609 2784.4 346.66
- relevel(Status, "No disease")  1   173.374 2959.4 348.76
- Age                            1   179.152 2965.2 348.95

Step:  AIC=343.53
TestC ~ Age + relevel(Status, "No disease") + TestA + TestB

                                Df Sum of Sq    RSS    AIC
- TestA                          1    34.031 2842.8 342.74
- TestB                          1    52.725 2861.5 343.39
<none>                                       2808.8 343.53
+ Timeinterval_AC                1    22.706 2786.1 344.72
+ relevel(Sex, "Male")           1    21.158 2787.6 344.78
+ Timeinterval_BC                1     0.136 2808.6 345.53
- relevel(Status, "No disease")  1   150.671 2959.4 346.76
- Age                            1   172.631 2981.4 347.50

Step:  AIC=342.74

TestC ~ Age + relevel(Status, "No disease") + TestB
#最后是这三个变量纳入了模型中，与向后法的结果是一样的
                                Df Sum of Sq    RSS    AIC
<none>                                       2842.8 342.74
- TestB                          1    73.205 2916.0 343.28
+ TestA                          1    34.031 2808.8 343.53
+ relevel(Sex, "Male")           1    28.190 2814.6 343.74
+ Timeinterval_AC                1    24.177 2818.6 343.88
+ Timeinterval_BC                1     0.385 2842.4 344.72
- relevel(Status, "No disease")  1   171.833 3014.6 346.61
- Age                            1   210.514 3053.3 347.88

2、全子集回归

  • 估计p²-1个回归模型，p是原始完整模型中变量个数
  • 对于每一个变量个数，展示最优的k个模型   regsubsets（y ~ x ，nbest =3） K=3
  • 可以根据预先设定的最终模型中变量数选择模型
  • 或者选择拟合表现最佳的模型作为最终模型
#2、全子集回归
#需要使用leaps拓展包
library('leaps')
model.all <- regsubsets(TestC ~ Age + relevel(Sex,"Male") + 
                          relevel(Status,"No disease") + TestA +
                          TestB + Timeinterval_AC + Timeinterval_BC,
                        nbest = 3,data = data.wide)
plot(model.all,scale = 'adjr2') #根据调整后的R方来进行排序

  • 该图以R方进行排序展示
  • 图中空白的部分表示这个变量没有被选择

3、LASSO回归

  • Lasso：Least absolute shrinkage and selection operator
  • 顾名思义：通过缩小回归系数来达到变量筛选的目的，核心思想是β的绝对值越小越好，所以在回归模型最小化残差和的基础上加入系数的绝对值的和，作为一个惩罚项，λ是调节系数，调节惩罚力度的大小，惩罚力度越大，β的绝对值越小，逐渐增大λ的话，β最小可以达到0，此时，该变量可以从模型中剔除
  • 对于每一个λ的值都对应着一组模型系数的估计，当我们使用Lasso时最核心的问题是如何选择合适的λ，通常我们可以通过交叉验证来寻找最优模型。
  • 目标：使残差平方的均值加λ倍回归系数绝对值的和最小化的β
  • 可以避免过度拟合的问题，同时通过将一些β缩减为0，达到变量筛选的目的
#3、Lasso回归
#Lasso无法识别分类变量，因此应该对分类变量进行转换
data.wide$Sex_num <- as.numeric(data.wide$Sex)
data.wide$Status_num <- as.numeric(data.wide$Status)

#Lasso无法识别数据框的，因此需要将数据框转换成矩阵
tem.x <- model.matrix(~.,data.wide[c('Age',"Sex_num",'Status_num','TestA','TestB',
                                     'Timeinterval_AC','Timeinterval_BC')])
tem.y <- data.wide$TestC

#拟合模型
library('glmnet')
model.lasso <- glmnet(tem.x,tem.y,family = 'gaussian',nlambda = 50,alpha = 1,
                      standardize = TRUE )
#nlambda = 表示给出多少个λ作为input，如果λ比较小，则会被忽略掉
model.lasso #一共有34个λ显示出来

#如何提取出对应的模型呢？当这个λ处于第20行的时候
coef(model.lasso,s = model.lasso$lambda[20])
#也可以选择λ是任意一个数字
coef(model.lasso ,s=0.1)

#通过交叉验证来选取最优的λ
cv.model <- cv.glmnet(tem.x,tem.y,family = 'gaussian',nlambda = 50,alpha = 1,
                      standardize = TRUE)
plot(cv.model)
#把最优的λ放入模型之后，模型的形式
cv.model$lambda.min
coef(cv.model,s = cv.model$lambda.min)
> model.lasso

Call:  glmnet(x = tem.x, y = tem.y, family = "gaussian", alpha = 1,      nlambda = 50, standardize = TRUE) 

   Df  %Dev  Lambda
1   0  0.00 2.73700
2   1  6.06 2.26800
3   2 11.30 1.88000
4   3 15.88 1.55800
5   3 19.24 1.29100
6   4 21.66 1.06900
7   4 23.49 0.88620
8   5 24.88 0.73440
9   5 25.87 0.60850
10  5 26.54 0.50420
11  5 27.01 0.41780
12  5 27.32 0.34620
13  6 27.73 0.28690
14  6 28.02 0.23770
15  6 28.21 0.19700
16  6 28.35 0.16320
17  6 28.44 0.13530
18  6 28.51 0.11210
19  6 28.55 0.09289
20  6 28.58 0.07697
21  6 28.60 0.06378
22  7 28.62 0.05285
23  7 28.63 0.04379
24  7 28.64 0.03629
25  7 28.65 0.03007
26  7 28.65 0.02492
27  7 28.65 0.02065
28  7 28.66 0.01711
29  7 28.66 0.01418
30  7 28.66 0.01175
31  7 28.66 0.00974
32  7 28.66 0.00807
33  7 28.66 0.00668
34  7 28.66 0.00554

上述结果可以看出，当λ逐渐增大时，模型中的变量（可以看Df这一列）逐渐减少 ，最终减少到0个。

> #如何提取出对应的模型呢？当这个λ处于第20行的时候
> coef(model.lasso,s = model.lasso$lambda[20])
9 x 1 sparse Matrix of class "dgCMatrix"
                          s1
(Intercept)     -5.374122356
(Intercept)      .          
Age              0.153423761
Sex_num          0.925142722
Status_num       2.842768704
TestA            0.069927177
TestB            0.079936017
Timeinterval_AC  0.001361324
Timeinterval_BC  .

 可以看到第20行的λ的模型中，TestB和TestC的时间间隔这一变量被排除掉了，一共剩下6个变量

#也可以选择λ是任意一个数字
> coef(model.lasso ,s=0.1)
9 x 1 sparse Matrix of class "dgCMatrix"
                          s1
(Intercept)     -5.205770685
(Intercept)      .          
Age              0.152478952
Sex_num          0.896363158
Status_num       2.790429259
TestA            0.068603375
TestB            0.079485001
Timeinterval_AC  0.001243166
Timeinterval_BC  .

上图表示的是交叉验证中得到的均方误差的平均值，平均值最低的点则是在交叉验证中得到误差最小的模型，上面的X轴对应的是模型中有几个变量，下面的轴对应着log（λ）的值。

cv.model$lambda.min
[1] 0.2377437
> coef(cv.model,s = cv.model$lambda.min)
9 x 1 sparse Matrix of class "dgCMatrix"
                           s1
(Intercept)     -4.1989080665
(Intercept)      .           
Age              0.1468281428
Sex_num          0.7242402783
Status_num       2.4774067224
TestA            0.0606861735
TestB            0.0767877474
Timeinterval_AC  0.0005365002
Timeinterval_BC  .

 以上为最优的模型

三、变量相对重要程度

1、根据标准化回归系数

  • \beta _{i}^{*} = \beta _{i}\cdot \sigma _{x_{i}}/\sigma _{y}
  • 标准化后β不受自变量本身尺度的影响
  • 标准化系数绝对值的大小，可以作为变量相对重要程度
#标准化回归系数
library('QuantPsyc')
#lm.beta()当存在交互项时，此函数不会产生“正确”的标准化系数,且模型中存在分类变量时可能会出错
model.full1 <- lm(TestC ~ Age+ Sex_num + Status_num +TestA+TestB+
                    + Timeinterval_AC + Timeinterval_BC,data = data.wide)
summary(model.full1) #Estimate 这一列为未标准化的回归系数
lm.beta(model.full1) #可以根据标准化回归系数来判断重要程度的大小
> model.full1 <- lm(TestC ~ Age+ Sex_num + Status_num +TestA+TestB+
+                     + Timeinterval_AC + Timeinterval_BC,data = data.wide)
> summary(model.full1) #Estimate 这一列为未标准化的回归系数

Call:
lm(formula = TestC ~ Age + Sex_num + Status_num + TestA + TestB + 
    +Timeinterval_AC + Timeinterval_BC, data = data.wide)

Residuals:
    Min      1Q  Median      3Q     Max 
-10.023  -3.490  -1.278   2.018  20.995 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)  
(Intercept)     -5.9909492  2.9135620  -2.056   0.0426 *
Age              0.1573773  0.0657161   2.395   0.0187 *
Sex_num          1.0035402  1.1837097   0.848   0.3988  
Status_num       3.0529009  1.3386101   2.281   0.0249 *
TestA            0.0724004  0.0820032   0.883   0.3796  
TestB            0.0809508  0.0757371   1.069   0.2879  
Timeinterval_AC  0.0018494  0.0020716   0.893   0.3743  
Timeinterval_BC -0.0002878  0.0020936  -0.137   0.8910  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.48 on 92 degrees of freedom
Multiple R-squared:  0.2866,	Adjusted R-squared:  0.2323 
F-statistic:  5.28 on 7 and 92 DF,  p-value: 4.265e-05

> lm.beta(model.full1)
            Age         Sex_num      Status_num           TestA           TestB 
     0.25814554      0.08056361      0.24032566      0.08789665      0.11374439 
Timeinterval_AC Timeinterval_BC 
     0.09013299     -0.01311310

标准化回归系数的绝对值越大，其对因变量的影响程度越大 

2、 根据解释R平方的比例

  • 即自变量对因变量解释的比例
  • 对因变量y的方差解释的越多的自变量越重要
#根据解释R方的比例,根据lmg方法来进行计算排序

calc.relimp(model.full,type = 'lmg',rela=TRUE)
#交叉验证画图

boot <- boot.relimp(model.full,b=1000,type ='lmg',
                    rank = TRUE, diff = TRUE,rela = TRUE) #b为1000次的重抽样
plot(booteval.relimp(boot,sort= TRUE))
calc.relimp(model.full,type = 'lmg',rela=TRUE)
Response variable: TestC 
Total response variance: 39.12021 
Analysis based on 100 observations 

7 Regressors: 
Age relevel(Sex, "Male") relevel(Status, "No disease") TestA TestB Timeinterval_AC Timeinterval_BC 
Proportion of variance explained by model: 28.66%
Metrics are normalized to sum to 100% (rela=TRUE). 

Relative importance metrics: 

                                      lmg
Age                           0.344205144
relevel(Sex, "Male")          0.080041755
relevel(Status, "No disease") 0.259730915
TestA                         0.116550625
TestB                         0.183541889
Timeinterval_AC               0.014202039
Timeinterval_BC               0.001727633

Average coefficients for different model sizes: 

                                         1X           2Xs          3Xs          4Xs
Age                            0.2681592815  0.2398042330 0.2162440873 0.1966306906
relevel(Sex, "Male")           3.0966987179  2.4056619102 1.9175543903 1.5724745182
relevel(Status, "No disease")  4.7565833333  4.1931093103 3.7826647967 3.4870003783
TestA                          0.2463373315  0.1963814582 0.1583886695 0.1292002703
TestB                          0.2591421181  0.2152695373 0.1791253420 0.1487873355
Timeinterval_AC               -0.0010788597 -0.0001975656 0.0003949433 0.0008353692
Timeinterval_BC               -0.0001472135  0.0001974354 0.0002799551 0.0002346903
                                       5Xs           6Xs           7Xs
Age                           0.1805027703  1.675086e-01  0.1573773335
relevel(Sex, "Male")          1.3263255624  1.144162e+00  1.0035402226
relevel(Status, "No disease") 3.2791649777  3.139317e+00  3.0529008514
TestA                         0.1063964169  8.798450e-02  0.0724003911
TestB                         0.1229908774  1.006930e-01  0.0809507694
Timeinterval_AC               0.0012006675  1.531493e-03  0.0018494318
Timeinterval_BC               0.0001136656 -6.309587e-05 -0.0002877852

 

也可以通过交叉验证来看自变量的相对重要程度以及其置信区间

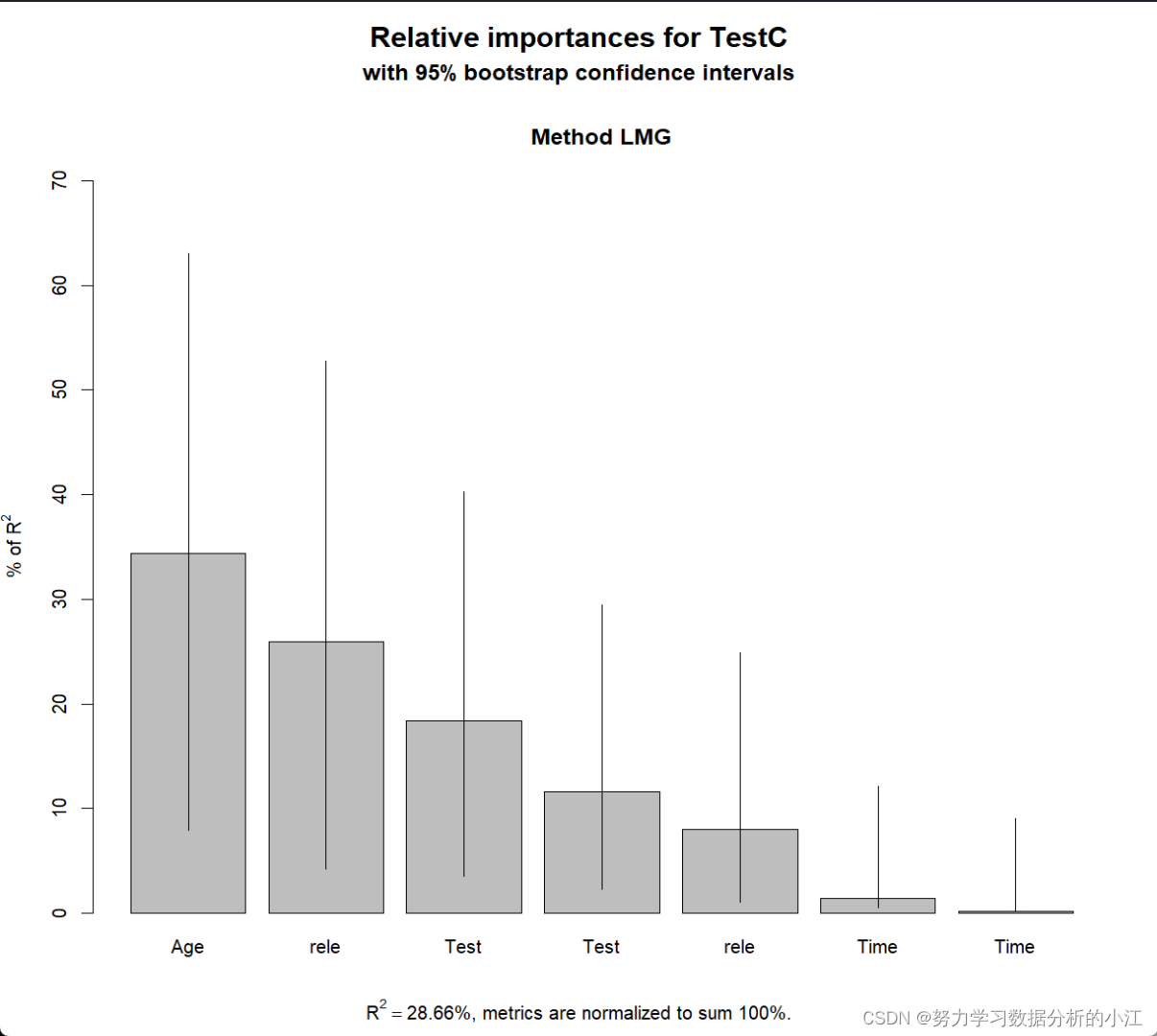
由上图可以看到，年龄是最重要的影响因素

3、根据Lasso保留变量的顺序

#根据Lasso保留变量的顺序
plot(model.lasso,xvar ='lambda',label=TRUE)

#也可以根据之前Lasso结果中的变量数量来列举比较
# 1个变量
coef(model.lasso,s= model.lasso$lambda[2])
# 2个变量
coef(model.lasso,s= model.lasso$lambda[3])
# 3个变量
coef(model.lasso,s= model.lasso$lambda[5])
# 4个变量
coef(model.lasso,s= model.lasso$lambda[7])
# 5个变量
coef(model.lasso,s= model.lasso$lambda[12])
# 6个变量
coef(model.lasso,s= model.lasso$lambda[21])
# 7个变量
coef(model.lasso,s= model.lasso$lambda[34])

下方x轴：log（λ）

上方x轴：模型中变量个数

先被排除的变量，相对不重要

倒过来看（从右往左看），当纳入第一个变量时，往往是最重要的，可以根据纳入的顺序来判断变量的相对重要程度

也可以通过列举模型来判断

 #也可以根据之前Lasso结果中的变量数量来列举比较
> # 1个变量
> coef(model.lasso,s= model.lasso$lambda[2])
9 x 1 sparse Matrix of class "dgCMatrix"
                        s1
(Intercept)     5.41345903
(Intercept)     .         
Age             0.04595103
Sex_num         .         
Status_num      .         
TestA           .         
TestB           .         
Timeinterval_AC .         
Timeinterval_BC .         
> # 2个变量
> coef(model.lasso,s= model.lasso$lambda[3])
9 x 1 sparse Matrix of class "dgCMatrix"
                        s1
(Intercept)     3.66188107
(Intercept)     .         
Age             0.07828682
Sex_num         .         
Status_num      0.33212324
TestA           .         
TestB           .         
Timeinterval_AC .         
Timeinterval_BC .         
> # 3个变量
> coef(model.lasso,s= model.lasso$lambda[5])
9 x 1 sparse Matrix of class "dgCMatrix"
                        s1
(Intercept)     1.03918698
(Intercept)     .         
Age             0.10928443
Sex_num         .         
Status_num      1.14927568
TestA           .         
TestB           0.02952812
Timeinterval_AC .         
Timeinterval_BC .         
> # 4个变量
> coef(model.lasso,s= model.lasso$lambda[7])
9 x 1 sparse Matrix of class "dgCMatrix"
                         s1
(Intercept)     -0.62805039
(Intercept)      .         
Age              0.12514357
Sex_num          .         
Status_num       1.65871945
TestA            0.01964364
TestB            0.05241481
Timeinterval_AC  .         
Timeinterval_BC  .         
> # 5个变量
> coef(model.lasso,s= model.lasso$lambda[12])
9 x 1 sparse Matrix of class "dgCMatrix"
                         s1
(Intercept)     -3.41206920
(Intercept)      .         
Age              0.14237270
Sex_num          0.58878845
Status_num       2.23545926
TestA            0.05442458
TestB            0.07461200
Timeinterval_AC  .         
Timeinterval_BC  .         
> # 6个变量
> coef(model.lasso,s= model.lasso$lambda[21])
9 x 1 sparse Matrix of class "dgCMatrix"
                          s1
(Intercept)     -5.470551028
(Intercept)      .          
Age              0.153967753
Sex_num          0.941628925
Status_num       2.872678538
TestA            0.070683137
TestB            0.080194129
Timeinterval_AC  0.001428962
Timeinterval_BC  .          
> # 7个变量
> coef(model.lasso,s= model.lasso$lambda[34])
9 x 1 sparse Matrix of class "dgCMatrix"
                           s1
(Intercept)     -5.9438791015
(Intercept)      .           
Age              0.1570712909
Sex_num          0.9985876540
Status_num       3.0356976210
TestA            0.0722868377
TestB            0.0809038366
Timeinterval_AC  0.0018104815
Timeinterval_BC -0.0002573162

#以上内容均来自医咖会R语言基础课程的个人笔记，仅供参考

使用ANOVA比较两个模型的差异（R语言）
DevGOOD的博客
08-25 1314
在统计学和数据分析中，ANOVA（方差分析）是一种常用的方法，用于比较多个组或条件之间的平均差异。在R语言中，我们可以使用ANOVA来比较两个模型之间的差异。本文将介绍如何使用ANOVA进行模型比较，并提供相应的源代码。通过使用ANOVA和多重比较，我们可以比较两个模型之间的差异，并确定是否存在显著性差异。我们的目标是比较这两个模型的平均观测值是否有显著差异。如果两个模型之间的显著性水平小于设定的显著性水平，则可以得出结论认为这两个模型之间存在显著差异。接下来，我们可以使用ANOVA函数进行模型比较。
R语言使用方差分析ANOVA比较回归模型的差异、anova函数比较两个模型并报告它们是否存在显著差异（两个模型的数据相同，一个模型使用的预测特征包含另外一个模型的特征）
statistics+insight+vista+power
07-30 2369
R语言使用方差分析ANOVA比较回归模型的差异、anova函数比较两个模型并报告它们是否存在显著差异（两个模型的数据相同，一个模型使用的预测特征包含另外一个模型的特征）
回归分析常数项t值没有显著异于零怎么办_R相关与回归学习笔记（二十二）——嵌套模型的比较...
weixin_39905725的博客
11-20 1277
本笔记中原始数据及代码均来源于李东风先生的R语言教程，在此对李东风先生的无私分享表示感谢。如果两个多元线性回归模型，第一个模型中的自变量都在第二个模型中，且第二个模型具有更多的自变量，则称第一个模型嵌套在第二个模型中。 例如：第一个模型中自变量为x1,x2,x3,第二个模型自变量为x1,x2,x3,x4,x5，则第一个模型嵌套在第二个模型中。又如：第一个模型自变量为x1,x2...
用于多个比较的方差分析（ANOVA）
timothyzh的专栏
06-17 1万+
Source: http://www.r-bloggers.com/analysis-of-variance-anova-for-multiple-comparisons/   用于多个比较的方差分析（ANOVA：Analysis of variance） ANOVA模型能用于比较多个群组之间的均值，这里使用了参数（parametric）的方法，也就是假设这些群组符合Gaussian分布。以
计量经济学名词解释
qq_47326711的博客
05-17 1万+
计量经济学名词解释第二章第三章第四章第五章第六章第七章第八章第九章第十章 第二章 普通最小二乘法（OLS）：通过最小化误差的平方和寻找数据的最佳函数匹配。 广义最小二乘法（GLS）：通过对原始模型的变换，解释了误差方差的方差已知结构（异方差性）、误差中的序列相关形式或同时解释二者的估计量。 加权最小二乘法（WLS）：用了对某种已知形式的异方差进行调整的估计量。其中，每个残差的平方都用一个等于误差的（估计的）方差的倒数作为权数。 解释平方和（SSE）：多元回归模型中度量拟合值的样本变异。 高斯马尔科夫假定（横
逻辑回归临床预测模型lasso回归变量筛选roc曲线定制Delong检验
10-10
本主题主要探讨了如何利用逻辑回归配合LASSO（Least Absolute Shrinkage and Selection Operator）回归进行变量筛选，以及如何定制ROC（Receiver Operating Characteristic）曲线进行模型评估，并采用Delong检验来...
基于MIV的神经网络变量筛选-基于BP神经网络的变量筛选
09-05
基于MIV的神经网络变量筛选是优化BP神经网络模型的重要手段，它通过选择最具代表性且互不冗余的变量，提高了模型的效率和精度。在实际操作中，结合具体的业务场景和数据特性，合理运用这种方法可以极大地提升模型的...
python回归模型 变量筛选_SPSS分析技术：回归模型的自变量筛选方法；
weixin_39849894的博客
12-06 2581
原标题：SPSS分析技术：回归模型的自变量筛选方法；欢迎关注天善智能微信公众号，我们是专注于商业智能BI，大数据，数据分析领域的垂直社区。 对商业智能BI、大数据分析挖掘、机器学习，python，R等数据领域感兴趣的同学加微信：tstoutiao，邀请你进入头条数据爱好者交流群，数据爱好者们都在这儿。基础回顾上篇文章，我们以两个自变量的分析案例为例，介绍了如果使用SPSS进行多重线性分析，如果是新...
matlab神经网络源码集锦- 神经网络变量筛选—基于BP的神经网络变量筛选
05-17
在数据分析和机器学习中，变量筛选是关键步骤，它有助于减少模型复杂度，提升模型的泛化能力，同时避免过拟合。 首先，我们需要理解BP神经网络的工作原理。BP神经网络由输入层、隐藏层和输出层构成，通过反向传播...
使用R语言进行方差分析（ANOVA、ANCOVA）（一）
amyniez的博客，欢迎交流讨论
04-16 1万+
方差分析是检验多个总体的均值是否相等来判断分类型自变量对数值型因变量是否有影响。它的优点是可以增加分类的可靠性。如果要研究4个总体的均值那么要两两比较需要比较6次，如果每次犯第一类错误的概率都是0.05，那么随着实验次数的增多会增大犯错误的概率。一般来说，随着增加个体显著性检验的次数，偶然因素导致差别的可能性也会增大(并非均值真的存在差别)，而方差分析就是同时考虑所有的样本，因此排除了错误累积的概率，从而避免拒绝一个真实的原假设。
R中的假设检验（三）相关与回归
clancy_wu的博客
02-02 3013
学到哪儿写到哪儿，这篇后面会随时更新。 一、相关分析 研究变量与变量间的关系就需要分析其相关性，就需要使用相关分析，相关分析比较简单。它分为皮尔逊相关、斯皮尔曼相关、肯德尔等级相关，并且他们有各自的适用范围：（1）Pearson，皮尔逊积差相关系数，适用于两个变量为连续变量，且两个变量需要严格符合正态性分布，由于其严格的条件所以其具有较强的统计效能。（2）Spearman，斯皮尔曼相关系数，对两个...
使用ANOVA函数比较两个模型并检测它们之间是否存在显著差异（R语言）
2301_79326559的博客
08-29 1801
现在我们想要比较这两个模型，并判断它们之间是否存在显著差异。如果P值小于预先设定的显著性水平（通常为0.05），则可以得出结论认为两个模型之间存在显著差异，即至少有一个模型的回归系数与其他模型不同。需要注意的是，ANOVA分析的前提条件之一是模型的满足独立性、线性性、等方差性和正态分布的假设。通过这种方式，我们可以评估不同模型之间的性能，并选择最合适的模型来解释数据。希望这篇文章能够帮助你理解如何使用ANOVA函数比较两个模型，并判断它们之间是否存在显著差异。函数分别拟合了模型A和模型B，并将它们保存在。
R语言统计分析——方差分析之ANOVA模型拟合
最新发布
maizeman126的博客
08-30 889
例如，对于双因素方差分析，若不同处理方式中的观测数不同，那么模型y~A*B与模型y~B*A的结果不同。例如，含因子A、B和因变量y的双因素不平衡因子设计，有三种效应：A的主效应、B的主效应、A和B的交互效应。，接着是双因素的交互项，再是三因素的交互项，以此类推。如上式中：A不做调整，B根据A做调整，A:B交互项根据A和B调整。A根据B调整，B依据A调整，A:B交互项同时根据A和B调整。A根据B和A:B做调整，A:B交互项根据A和B调整。③控制A和B的主效应时，A与B的交互效应。②控制A时，B对y的影响；
R语言使用anova函数进行方差分析比较两个回归分析模型的差异、从而决定是否删除某些预测变量(Comparing nested models using the anova function)
data+scenario+science+insight
01-16 3433
R语言使用anova函数进行方差分析比较两个回归分析模型的差异、从而决定是否删除某些预测变量(Comparing nested models using theanova function)
python统计分析——单因素方差分析
maizeman126的博客
02-25 3859
如果连续进行2次检验，则每次检验的显著性水平都为0.05，在这种情况下，出现第一类错误的概率就是1-0.95*0.95=0.0975，约为10%，超过了5%。beer=7.0-4.0*rainy+4.0*sunny，解释为：当weather为cloudy时，beer=7.0-4.0*0+4.0*0=7.0；变量sunny同理。当然还有cloudy天气，当rainy和sunny均为0时，只剩下β0，它代表cloudy的影响程度。1.4 如下面的小提琴图所示：小提琴之间的高度差，即效应的大小，叫作组间差异。
机器学习中的变量选择——进阶篇
热门推荐
管他叫大靖
03-03 2万+
机器学习中的变量选择变量选择回顾单变量筛选通过模型选择变量变量选择进阶只用模型就能选好变量么数据处理模型介绍实验结果认识伪相关两步法估计 变量选择回顾 符号说明： p:p:p: 特征数量 n:n:n: 样本数量 变量选择在机器学习中扮演着重要的角色，无论是对于构建一个可解释的模型，还是提升模型的预测能力。 单变量筛选 在高维情况下，有时候我们需要预先筛选部分变量，然后再训练模型。筛选过程需要做到...
R语言结构方程模型SEM、路径分析房价和犯罪率数据、预测智力影响因素可视化2案例
大数据部落
01-14 2167
原文链接：http://tecdat.cn/?p=25044 原文出处：拓端数据部落公众号 1 简介 在本文，我们将考虑观察/显示所有变量的模型，以及具有潜在变量的模型。第一种有时称为“路径分析”，而后者有时称为“测量模型”。 2 进行简单的多元回归 SEM 在很大程度上是回归的多元扩展，我们可以在其中一次检查许多预测变量和结果。SEM 还提供了检查潜在结构（即未观察到某些变量的地方）的创新。更具体地说，“结构方程”的概念是指我们有不止一个方程表示协方差结构模型，其中我们（通常）有多个标准变量
统计学基础14-方差分析
只是甲的博客
05-17 1427
文章目录一. 方差分布概述二. 单因素方差分析2.1 检验统计量2.2 One-way ANOVA model2.3 多重比较试验三.多因素方差分析参考: 一. 方差分布概述 方差分布服从F分布 F分布的分位点: 二. 单因素方差分析 前提条件: 各个总体是(近似)正态分布 各个总体具有相等方差 样本是随机样本 各个样本间相互独立 单因素试验 2.1 检验统计量 例子: 2.2 One-way ANOVA model [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(im
如何使用R语言拟合ANOVA模型
Mrrunsen的博客
05-27 2722
如何使用R语言拟合ANOVA模型 aov()函数： R语言用于拟合ANOVA模型的函数为aov()，它的语法结构为aov(formula, data=dataframe)。函数有两个参数需要指定，分别为formula和data，formula为待指定的公式，data为待指定的数据。 R语言formula格式一般是这样的：y ~ A。波浪号左边表示因变量，右边表示自变量（或称因素）。 如果有A、B、C多个分组自变量，formula可以写作：y~A+B+C; 如果两个自变量间存在交互效应（如B与C），
临床预测模型变量筛选
08-28
在临床预测模型中，变量筛选的方法通常是将单因素有意义的变量纳入预测模型中。 这意味着只有那些与预测结果有显著相关性的变量才会被考虑。具体的建模方法可以是logistic回归模型，这是一种广义线性模型（GLM）。 在一个临床预测模型的研究中，作者使用了“10个样本一个变量”的标准来计算样本量。 这意味着对于每一个要考虑的变量，至少需要有10个样本。这个标准的目的是确保模型的稳定性和可靠性。 另外，在变量筛选过程中，作者使用了AUC（曲线下面积）来评估模型的性能。AUC是一种广泛应用于评估二分类模型的指标，它可以衡量模型对于正确分类样本的能力。 综上所述，在临床预测模型中，变量筛选的方法通常是基于单因素的显著性并且纳入预测模型，使用广义线性模型（如logistic回归模型），并且样本量的计算可能遵循特定的标准，最后使用AUC来评估模型的性能。<span class="em">1</span><span class="em">2</span><span class="em">3</span> #### 引用[.reference_title] - *1* [Topic 4. 临床预测模型构建 Logistic 回归](https://blog.csdn.net/weixin_41368414/article/details/122363341)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_item style="max-width: 50%"] - *2* *3* [R数据分析：跟随top期刊手把手教你做一个临床预测模型](https://blog.csdn.net/tm_ggplot2/article/details/121409367)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip_chatgpt_common_search_pc_result","utm_medium":"distribute.pc_search_result.none-task-cask-2~all~insert_cask~default-1-null.142^v93^chatsearchT3_1"}}] [.reference_item style="max-width: 50%"] [ .reference_list ]
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值