优先级队列(堆)(java数据结构)_java 实现优先队列-优快云博客

本文链接：https://blog.youkuaiyun.com/2301_76815082/article/details/143492583

1. 概念

前面介绍过队列，队列是一种先进先出(FIFO)的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列，该中场景下，使用队列显然不合适，比如：在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话；初中那会班主任排座位时可能会让成绩好的同学先挑座位。

在这种情况下，数据结构应该提供两个最基本的操作，一个是返回最高优先级对象，一个是添加新的对象。这种数结构就是优先级队列(Priority Queue)。

1.2. 优先级队列的模拟实现

JDK1.8中的PriorityQueue底层使用了堆这种数据结构，而堆实际就是在完全二叉树的基础上进行了一些调整。(也就是说,优先级队列的底层实现是一颗完全二叉树)

2.堆的概念

如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为小堆(或大)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：
1.堆中某个节点的值总是不大于或不小于其父节点的值；
2.堆总是一棵完全二叉树。

上面的概念就是说堆的底层是一颗完全二叉树,这里又把完全二叉树分类,分为大根堆和小根堆 .

这里我们就会疑惑,什么是大根堆,什么又是小根堆呢?

如上图:

在小根堆的示例中我们发现,他的根节点一定是小于左右孩子的所有节点 (如上图,根节点10,小于左子树15和右子树56,后面左子树右子树亦是如此),这里我们需要注意的是,左右孩子谁最小没有关系,我们只考虑根和左右孩子的关系.

在大根堆的示例中我们发现,他的根节点一定是大于左右孩子的所有节点 (如上图,根节点70,大于左子树56和右子树30,后面左子树右子树亦是如此),这里我们需要注意的是,不看左右孩子的大小,我们只考虑根和左右孩子的关系.

这里我们说的小根堆大根堆都是完全二叉树,这里存储的时候,就把他们存在了数组当中.

2.1堆的存储方式

从堆的概念可知，堆是一棵完全二叉树，因此可以层序的规则采用顺序的方式来高效存储，

注意：对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低。(就是说非完全二叉树就会浪费空间存在,如上一般二叉树的图)

讲到这里我们就要明白,我们说的PriorityQueue底层是一颗完全二叉树,而他要实现优先级队列一定要把这颗完全二叉树看成堆,堆又分为大根堆和小根堆.

2.2堆的创建 (此篇所有内容以大根堆为例)

所以接下来我们要做的就是如何自己实现这个优先级队列,用自己的方法把他创建成一个大根堆或者小根堆.

在这之前我们先来看一下如下性质:

将元素存储到数组中后，可以根据二叉树章节的性质5对树进行还原。假设i为节点在数组中的下标，则有：
如果i为0，则i表示的节点为根节点，否则i节点的双亲节点为 (i - 1)/2 (这里0指的是下标,如下图)
如果2 * i + 1 小于节点个数，则节点i的左孩子下标为2 * i + 1，否则没有左孩子 (就是说比如i是56,下标为2,2*i+1等于5,5小于节点个数6,则节点i的左孩子下标为5.比如i是25,下标为3,2*i+1等于7,不小于节点个数6,则25没有左孩子)
如果2 * i + 2 小于节点个数，则节点i的右孩子下标为2 * i + 2，否则没有右孩子

这里以大根堆为例:

以上图为例,目前上图只是一棵普通的二叉树,这里我们要做的是怎样把它变成大根堆?而大根堆意味着他的每颗子树都是大根49

这里我们要考虑的是,该如何找最大值呢?

这里让每颗子树变成大根堆的过程中,他的做法是找到左右孩子的最大值,然后让最大值和根节点交换(比如在18这棵树里面,找到左右孩子的最大值49,让他的最大值18和根节点18交换).

调整过程如下图:

总结一下调整过程:

1.这里是从子最后一棵子树开始调整的(如上我们是从下标4开始调整的)

2.找到左右孩子的最大值和根节点开始比较,如果根节点大,那么就交换

3.如果能够知道子树的根结点下标,那么下一棵子树就是当前根节点下标-1(如上我们先调节完 4下标,然后调节3下标,接下来调整2下标,然后调整1下标)

4.一直要调整到0下标这棵树就停止!

但是这里的问题是:

1.每颗子树调整的时候结束的位置怎么定?(怎么证明这棵树调整完了)

2.最后一颗子树的根节点下标怎么定?(这个简单,如上总共有10个节点,最后一个节点下标是9,而一直孩子节点推导父亲节点公式是(i-1)/2,而i又等于len-1 ((i-1)/2-->i=len-1) )

现在来探讨问题1,每颗子树结束的位置怎么定?

其实很简单,我们直接给一个len就好,这里我们就要想,为什么每颗子树的结束位置都和len有关系呢?如上图的长度为10,(这里有没有左右孩子都和节点个数有关),他不管走到左边还是右边,这里不管算的(2*i)+1还是(2*i)+2,只要超过或者等于10个节点(这里只有10个节点,没有10下标),说明没有右孩子,表示这个子树就走完了.所以这里我们就找这棵树的节点个数,而节点个数就是数组长度.

2.3堆向下调整

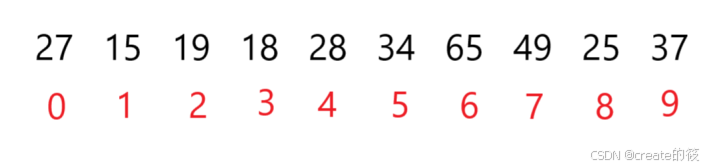
对于集合{ 27,15,19,18,28,34,65,49,25,37 }中的数据，如果将其创建成堆呢？

仔细观察上图后发现：根节点的左右子树已经完全满足堆的性质，因此只需将根节点向下调整好即可。

向下过程(以小堆为例)：

下面我们来写代码:

public class TestHeap {

    public int[] elem;
    public int usedSize;//记录当前堆当中 有效的数据个数

    public TestHeap() {
        this.elem = new int[10];//这里只是代表数组的大小为10,所以我们先初始化数组
    }

    /**
     * 初始化elem数组的
     * @param array
     */
    public void initElem(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }

    /**
     * 创建大根堆的代码
     * 如果 使用 向下调整创建大根堆  时间复杂度：O(N)
     */
    //最后一颗子树的下标是(i-1)/2-->i=len-1,所以usedSize-1-1指假如有大小为10,但是放了5个元素,注意的是这里不能是len-1,因为len包含了0,这里len-1=usedSize-1
    public void createHeap() {
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            siftDown(parent,usedSize);//这里放了两个参数指每颗子树和结束位置
        }
    }
    /**
     * 向下调整(每颗子树都是从根向下调整)
     * @param parent
     * @param len
     */
    private void siftDown(int parent,int len) {
        int child = 2*parent+1;
        while (child < len) {//防越界  (child < len说明 至少你有左孩子)
            //左孩子 和 右孩子 比较大小 如果右孩子的值大 就记录最大值
            if(child+1 < len && elem[child] < elem[child+1]) {
                child = child+1;
            }
            //走完上述if语句  证明 child下标 一定保存的是左右两个孩子最大值的下标
            if(elem[child] > elem[parent]) {
                //交换
                swap(child,parent);
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }
}

其中:

注意：在调整以parent为根的二叉树时，必须要满足parent的左子树和右子树已经是堆了才可以向下调整。
时间复杂度分析：

最坏的情况即上上图示的情况，从根一路比较到叶子，比较的次数为完全二叉树的高度，即时间复杂度为 O(log2n)

2.4建堆的时间复杂度

因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：

因此：建堆的时间复杂度为O(N)。

3. 堆的插入与删除

这里在堆中插入元素,插入之后,从下往上调整.删除堆中元素就从上往下调整

3.1 堆的插入

堆的插入总共需要两个步骤：

1. 先将元素放入到底层空间中(注意：空间不够时需要扩容)
2. 将最后新插入的节点向上调整，直到满足堆的性质

代码如下:

private void swap(int i,int j) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }

    public void push(int val) {
        //满了
        if(isFull()) {
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize] = val;
        //向上调整
        siftUp(usedSize);
        //
        usedSize++;//11
    }
    public boolean isFull() {
        return usedSize == elem.length;
    }
    public void siftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if (elem[child] > elem[parent]) {
                swap(child, parent);
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }





这里注意:向上调整的建堆复杂度比向下调整的建堆复杂度高一点

3.2 堆的删除

注意：堆的删除一定删除的是堆顶元素。具体如下：

1. 将堆顶元素(0下标)和堆中最后一个元素交换
2. 交换之后,将堆中有效数据个数减减,删除堆中最后一个元素
3. 只需要向下调整0下标这棵树,调整到满足堆特性为止

插入的时候要保证这个堆是一个大根堆,而删除的时候一定要删除优先级比较大的这个,如上的10,而且要删除的时候一定要保证他是大根堆

代码如下:

 public int pop() {
        //判空
        if(empty()) {
            return -1;
        }
        int oldVal = elem[0];
        swap(0,usedSize-1);
        usedSize--;
        siftDown(0,usedSize);
        return oldVal;
    }

    public boolean empty() {
        return usedSize == 0;
    }

完整代码如下:

import java.util.Arrays;

public class TestHeap {

    public int[] elem;
    public int usedSize;//记录当前堆当中 有效的数据个数

    public TestHeap() {
        this.elem = new int[10];//这里只是代表数组的大小为10,所以我们先初始化数组
    }

    /**
     * 初始化elem数组的
     * @param array
     */
    public void initElem(int[] array) {
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            usedSize++;
        }
    }

    /**
     * 创建大根堆的代码
     * 如果 使用 向下调整创建大根堆  时间复杂度：O(N)
     */
    //最后一颗子树的下标是(i-1)/2-->i=len-1,所以usedSize-1-1指假如有大小为10,但是放了5个元素,注意的是这里不能是len-1,因为len包含了0,这里len-1=usedSize-1
    public void createHeap() {
        for (int parent = (usedSize-1-1)/2; parent >= 0 ; parent--) {
            siftDown(parent,usedSize);//这里放了两个参数指每颗子树和结束位置
        }
    }
    /**
     * 向下调整(每颗子树都是从根向下调整)
     * @param parent
     * @param len
     */
    private void siftDown(int parent,int len) {
        int child = 2*parent+1;
        while (child < len) {//防越界  (child < len说明 至少你有左孩子)
            //左孩子 和 右孩子 比较大小 如果右孩子的值大 就记录最大值
            if(child+1 < len && elem[child] < elem[child+1]) {
                child = child+1;
            }
            //走完上述if语句  证明 child下标 一定保存的是左右两个孩子最大值的下标
            if(elem[child] > elem[parent]) {
                //交换
                swap(child,parent);
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }

    private void swap(int i,int j) {
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }



    public void push(int val) {
        //满了
        if(isFull()) {
            elem = Arrays.copyOf(elem,2*elem.length);
        }
        elem[usedSize] = val;
        //向上调整
        siftUp(usedSize);
        //
        usedSize++;//11
    }
    public boolean isFull() {

        return usedSize == elem.length;
    }
    public void siftUp(int child) {
        int parent = (child-1)/2;
        while (child > 0) {
            if (elem[child] > elem[parent]) {
                swap(child, parent);
                child = parent;
                parent = (child - 1) / 2;
            } else {
                break;
            }
        }
    }


    public int pop() {
        //判空
        if(empty()) {
            return -1;
        }
        int oldVal = elem[0];
        swap(0,usedSize-1);
        usedSize--;
        siftDown(0,usedSize);
        return oldVal;
    }

    public boolean empty() {

        return usedSize == 0;
    }


}

public class Text {
    public static void main(String[] args) {
        TestHeap testHeap = new TestHeap();
        int[] array = {27,15,19,18,28,34,65,49,25,37};
        testHeap.initElem(array);

        testHeap.createHeap();

        System.out.println(testHeap.pop());

        System.out.println("===");

    }
}

4.常见习题：

1.下列关键字序列为堆的是:(A)
A: 100,60,70,50,32,65 B: 60,70,65,50,32,100 C: 65,100,70,32,50,60
D: 70,65,100,32,50,60 E: 32,50,100,70,65,60 F: 50,100,70,65,60,32

这里没有告诉我们大堆小堆,自己动手

2.已知小根堆为8,15,10,21,34,16,12，删除关键字8之后需重建堆，在此过程中，关键字之间的比较次数是(C)
A: 1 B: 2 C: 3 D: 4

4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是(C)
A: [3，2，5，7，4，6，8] B: [2，3，5，7，4，6，8]
C: [2，3，4，5，7，8，6] D: [2，3，4，5，6，7，8]

5.常用接口介绍(下面来看一下Java当中的堆是什么样子)

5.1 PriorityQueue的特性

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue。

下面我们来演示一下 PriorityQueue是什么样的:

这里我们往这个优先级队列里面放几个元素,这里没人告诉我们他是大根堆还是小根堆,这里我们peek一下这个元素,看我们拿到的是10(大根堆)还是5(小根堆).

结果如下:

如上结果意味着,当我们实例化一个PriorityQueue对象之后，其实默认是一个小根堆.

关于PriorityQueue的使用要注意：

1. 使用时必须导入PriorityQueue所在的包，即：

import java.util.PriorityQueue;

2. PriorityQueue中放置的元素必须要能够比较大小，不能插入无法比较大小的对象，否则会抛出
ClassCastException异常

这里我们简单看个例子,如下代码:
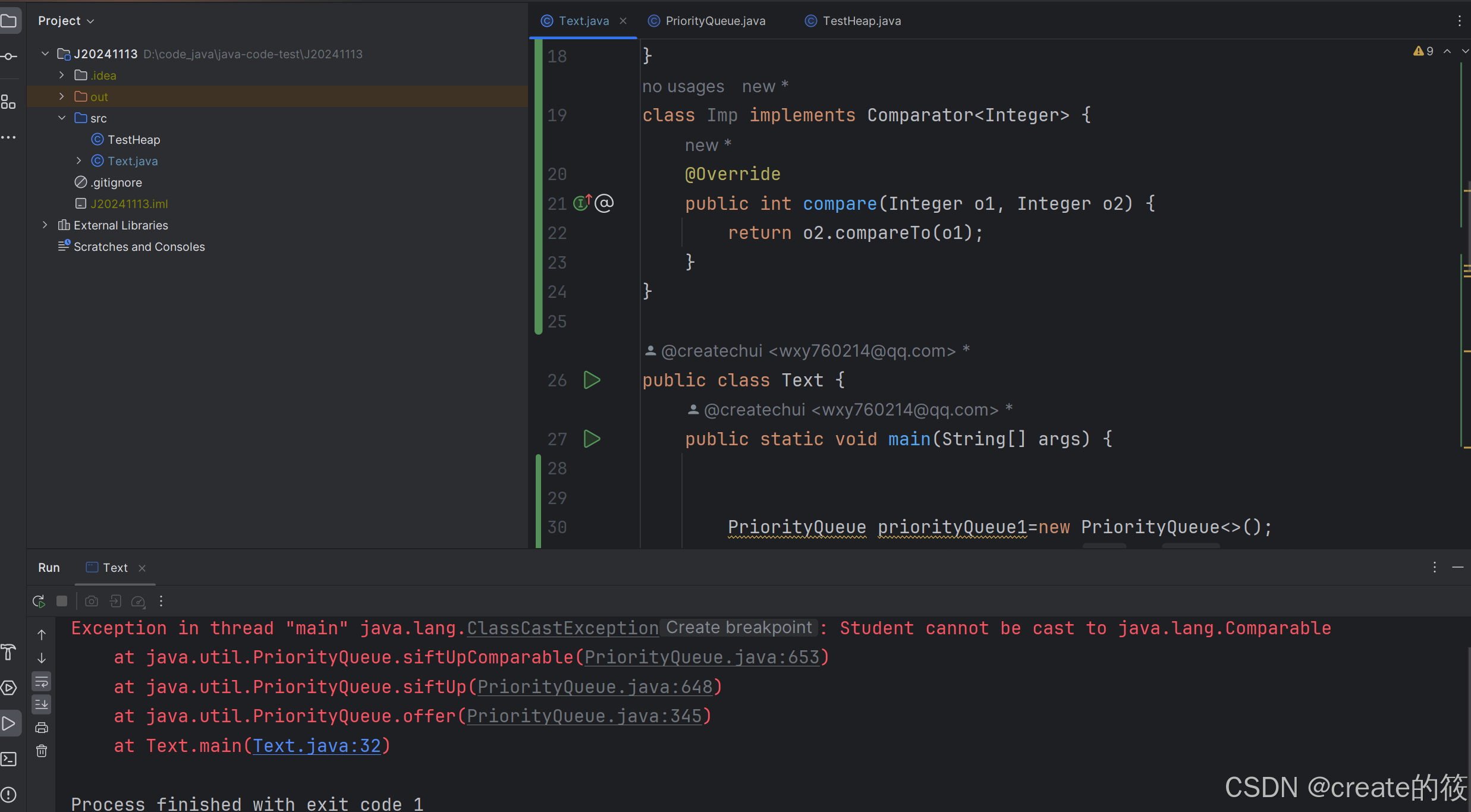
import java.util.Comparator;
import java.util.PriorityQueue;
class Student {
    public int age;
    public String name;

    public Student(int age, String name) {
        this.age = age;
        this.name = name;
    }
    @Override
    public String toString() {
        return "Student{" +
                "age=" + age +
                ", name='" + name + '\'' +
                '}';
    }
}
class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        return o2.compareTo(o1);
    }
}

public class Text {
    public static void main(String[] args) {


        PriorityQueue priorityQueue1=new PriorityQueue<>();
        priorityQueue1.offer(new Student(10,"张三"));
        priorityQueue1.offer(new Student(10,"王五"));
    }
如下结果:

这里我们发现运行结果报错了(类型转换错误),这里我们offer了两个学生,而push的时候这两个学生要进行比较,但是这里并没有告诉我们通过姓名比较还是通过年龄比较,所以他认为这里面是不能比较的.

这里如果我们屏蔽掉 priorityQueue1.offer(new Student(12,"王五")) 这段代码的时候就不会报错,原因是没有比较对象.这里该怎么做我们鼠标点击绿色画线.可以看到,自定义比较要加Comparable接口.

3. 不能插入null对象，否则会抛出NullPointerException

4. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容

堆相对于栈来说大一点

5. 插入和删除元素的时间复杂度均为o(log2N)
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素

5.2 PriorityQueue常用接口介绍

这里我们先来适当的看一下 PriorityQueue这个类的源码:

我们先从这个类的构造方法入手:这里 PriorityQueue的继承关系我们先不看了.

以下是他的成员变量:

(默认初始容量)

数组引用,将来用来存储数据(默认为null)

当前队列当中的有效数据的个数

绿色部分就是比较器,它默认为null

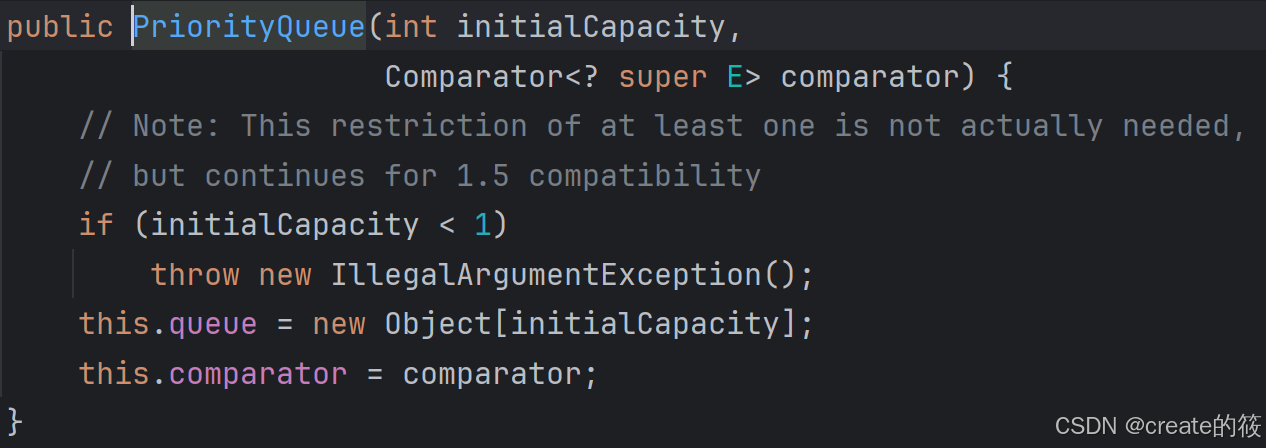
不带参的构造方法,如上我们看到,这个构造方法调用了带两个参数的构造方法,一个默认的初始容量11和一个空的比较器,如下是带两个参数的构造方法(按住ctrl,点击上图this)

带一个参数的构造方法(直接给容量)

直接传一个比较器

如上就是他构造方法相关的一些源码.

下面来看一下offer的源码,拿上面这三个为例,他是一个小根堆,这里证明一下他是小根堆.

上面(return(x<y)?-1:(x==y)?0:1))中x<y代表小根堆,当把他改成x>y就是大根堆.

根据上面源码代码,我们来演示一下把PriorityQueue变成大根堆或小根堆.

大根堆:

import java.util.Comparator;
import java.util.PriorityQueue;
class Student {
    public int age;
    public String name;

    public Student(int age, String name) {
        this.age = age;
        this.name = name;
    }
    @Override
    public String toString() {
        return "Student{" +
                "age=" + age +
                ", name='" + name + '\'' +
                '}';
    }
}
class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        
        return o2.compareTo(o1);
    }
}

public static void main(String[] args) {
        Imp imp=new Imp();
        // 当我们实例化一个PriorityQueue对象之后，其实默认是一个小根堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(imp);
        priorityQueue.offer(10);
        priorityQueue.offer(5);
        priorityQueue.offer(6);

//        System.out.println(priorityQueue.peek());

        System.out.println(priorityQueue.poll());//5
        System.out.println(priorityQueue.poll());//6
    }

小根堆:

import java.util.Comparator;
import java.util.PriorityQueue;
class Student {
    public int age;
    public String name;

    public Student(int age, String name) {
        this.age = age;
        this.name = name;
    }
    @Override
    public String toString() {
        return "Student{" +
                "age=" + age +
                ", name='" + name + '\'' +
                '}';
    }
}
class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {
        
        return o1.compareTo(o2);
    }
}

public static void main(String[] args) {
        Imp imp=new Imp();
        // 当我们实例化一个PriorityQueue对象之后，其实默认是一个小根堆
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(imp);
        priorityQueue.offer(10);
        priorityQueue.offer(5);
        priorityQueue.offer(6);

//        System.out.println(priorityQueue.peek());

        System.out.println(priorityQueue.poll());//5
        System.out.println(priorityQueue.poll());//6
    }

上面我们说到了扩容,下面我们来看一下grow这个方法的源码.

6.OJ练习

top-k问题：最大或者最小的前k个数据。比如：世界前500强公司

top-k问题：最小的K个数(topK问题往往求得都是在大量的数据里面最小的K个值,这个k往往非常小)

意思就是:比如有5个数据,这里找到这5个数据中的最小的三个数.

刚开始看到这个题(最小的k个数),我们的第一反是:

1.整体建立一个小根堆

2.出k次数据就找到了

思路代码如下:

public class Text {
    public static void main(String[] args) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
        int[] array = {10,3,15,7,19,9};

        //相当于是以向上调整的方式 建立小根堆 O(n*logn)
        for (int i = 0; i < array.length; i++) {
            priorityQueue.offer(array[i]);
        }

        int k = 3;
        int[] ret = new int[k];
        //k*logN
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }

        System.out.println(Arrays.toString(ret));
    }

代码结果:

如上代码可以通过,但是不是一个好的做法,因为速度比较慢(这里如果按照这种思路做,这里假如有一万个元素,他堆得大小就是一万个元素).而这里的解决思路就是,这里不要建这么大的堆.

举个例子:我们上面不是有27,15,19,18,28一共5个元素,如上图,这里我们的目标是找前k个最小的元素,刚刚上面我们建立的是一个小根堆,而现在要建立一个大根堆,这里不是整体建立一个大根堆,而是大小为k,这里我们先拿前三个建成一个大根堆,然后i走到3下标,然后从第k+1个元素开始比较,如果对顶元素小,则入堆.因为当前这个堆顶元素就不是我要的前K个最小的元素了(原理图如下),后面i++,原理一样.

下面我们来实现这个代码:

先来看一下IDEA上的:

import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
class Student {
    public int age;
    public String name;

    public Student(int age, String name) {
        this.age = age;
        this.name = name;
    }
    @Override
    public String toString() {
        return "Student{" +
                "age=" + age +
                ", name='" + name + '\'' +
                '}';
    }
}
class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {

        return o2.compareTo(o1);
    }
}

public class Text {
    public static int[] smallestK(int[] array, int k) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Imp());
            //1、建立大小为k的大根堆 O(K*logK)
        for (int i = 0; i < k; i++) {
                priorityQueue.offer(array[i]);
            }
        //2、遍历剩下的元素 (N-K)*logK
        // (K*logK) + N*logK  - K*logK   =   N*logK
        for (int i = k; i < array.length; i++) {
            int top = priorityQueue.peek();//27
            if(array[i] < top) {
                priorityQueue.poll();
                priorityQueue.offer(array[i]);
            }
        }
        //下面这个不能算topK的复杂度 这个地方是整理数据
        //k*logK
        int[] ret=new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        return ret;
    }

    public static void main(String[] args) {
        int[] array = {10,3,15,7,19,9};
        int[] ret=smallestK(array,3);
        System.out.println(Arrays.toString(ret));
    }




代码结果:9,7,3





这个代码和上面代码一样
class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {

        return o2.compareTo(o1);
    }

    public static int[] smallestK(int[] array, int k) {
        int[] ret = new int[k];
        if(array == null || k <= 0) {
            return ret;
        }
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o2.compareTo(o1);
            }
        });

        //1、建立大小为k的大根堆 O(K*logK)
        for (int i = 0; i < k; i++) {
            priorityQueue.offer(array[i]);
        }

        //2、遍历剩下的元素 (N-K)*logK
        // (K*logK) + N*logK  - K*logK   =   N*logK
        for (int i = k; i < array.length; i++) {
            int top = priorityQueue.peek();//27
            if(array[i] < top) {
                priorityQueue.poll();
                priorityQueue.offer(array[i]);
            }
        }
        //下面这个不能算topK的复杂度 这个地方是整理数据
        //k*logK
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        return ret;
    }

再来看一下力扣上面的:

class Imp implements Comparator<Integer> {
    @Override
    public int compare(Integer o1, Integer o2) {

        return o2.compareTo(o1);
    }
}

class Solution {
    public int[] smallestK(int[] array, int k) {
         int[] ret = new int[k];
        if(array==null || k<=0){
            return ret;

        }
         PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Imp());
        //相当于是以向上调整的方式 建立小根堆 O(n*logn)
       //1、建立大小为k的大根堆 O(K*logK)
        for (int i = 0; i < k; i++) {
            priorityQueue.offer(array[i]);
        }

        //2、遍历剩下的元素 (N-K)*logK
        // (K*logK) + N*logK  - K*logK   =   N*logK
        for (int i = k; i < array.length; i++) {
            int top = priorityQueue.peek();//27
            if(array[i] < top) {
                priorityQueue.poll();
                priorityQueue.offer(array[i]);
            }
        }
        //下面这个不能算topK的复杂度 这个地方是整理数据
        //k*logK
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        return ret;
    }
}

结果如下:

匿名内部类写法:

public class Text {
    public static int[] smallestK(int[] array, int k) {
        PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return 0;
            }
        });
            //1、建立大小为k的大根堆 O(K*logK)
        for (int i = 0; i < k; i++) {
                priorityQueue.offer(array[i]);
            }
        //2、遍历剩下的元素 (N-K)*logK
        // (K*logK) + N*logK  - K*logK   =   N*logK
        for (int i = k; i < array.length; i++) {
            int top = priorityQueue.peek();//27
            if(array[i] < top) {
                priorityQueue.poll();
                priorityQueue.offer(array[i]);
            }
        }
        //下面这个不能算topK的复杂度 这个地方是整理数据
        //k*logK
        int[] ret=new int[k];
        for (int i = 0; i < k; i++) {
            ret[i] = priorityQueue.poll();
        }
        return ret;
    }

7. 堆排序

这里我们先来思考一个问题:如果从小到大排序,应该建立大根堆还是小根堆?(应该建立大根堆)

举例:吧如上的的元素建成大根堆,建成大根堆之后,他把栈顶元素最大的元素和最后一个元素交换(如上第二幅图),也就是说最大的元素有序了,接着把这颗树进行调整为大根堆(如上第三幅图).再把49和15进行交换,接着把这颗树进行调整为大根堆.这里我们发现每次调整0下标就好了,所以我们这里定义一个end,每次让他和0下标交换,交换完之后end减减(只需要调整0下标,最后结束的位置就是end).

测试代码如下:

 public void heapSort() {
        int end = usedSize-1;
        while (end > 0) {
            swap(0,end);
            siftDown(0,end);
            end--;
        }


这段代码放在TestHeap这个类中

结果: