链表的复习

链表的基础操作：

重要的是画出图来，根据图上的步骤来进行对链表的操作。

203:移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

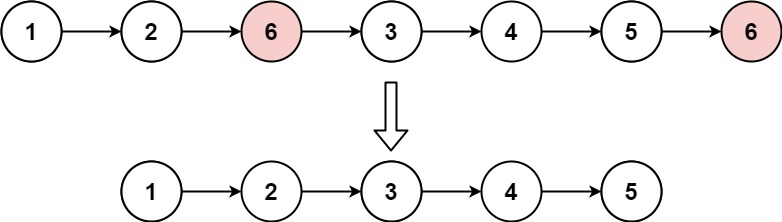
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

一、将头结点单独拿出来处理：

处理头结点的循环主要用于对当前节点进行检查并处理，使用一个while循环在遇到连续多个val排在链表头的情况进行处理。

处理非头结点的循环主要是用于对当前节点后面节点的检查 ,使用一个while循环来处理多个val连在一起的情况，内部使用一个if进行判断，如果是val就替换，不是则指针后移。

ListNode* removeElements(ListNode* head, int val) {
        // 处理头结点
        while(head != NULL && head -> val == val){
            ListNode* tmp = head;
            head = head -> next;
            delete tmp;
        }
        // 处理非头结点
        ListNode* cur = head;
        while(cur != NULL && cur -> next != NULL){
            if(cur -> next -> val == val){
                ListNode* tmp = cur -> next;
                cur -> next = cur -> next -> next;
                delete tmp;
            }else{
                cur = cur -> next;
            }
        }
        return head;
    }

二、使用虚拟指针将特殊情况普遍化 

为了不在将头结点的处理单独拎出来，我们需要在头结点前面加一个虚拟指针来处理，这样就没有了头结点，也不再需要对虚拟头结点进行特殊处理：

ListNode* removeElements(ListNode* head, int val) {
        // 设置一个虚拟头结点指向真正的头结点：
        ListNode* newhead = new ListNode(0);
        newhead->next = head;
        ListNode* cur = newhead;
        while(cur != NULL && cur->next != NULL){
            if(cur->next->val == val){
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            }else{
                cur = cur->next;
            }
        } 
        head = newhead->next;
        delete newhead;
        return head;
    }

206:翻转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

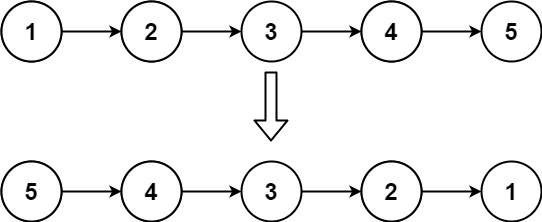
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

利用两个指针，一个指向头结点，一个指向头结点翻转后指向的空节点null，将头结点的next节点赋值给tmp临时指针，然后改变头结点next指向的位置为pre，然后移动两个指针倒下一个节点：

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* cur = head;
        ListNode* pre = nullptr;
        while(cur){
            ListNode* tmp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = tmp;
        }
        return pre;
    }
};

注意只有在删除节点时才需要delete，其他情况不需要。

24：两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

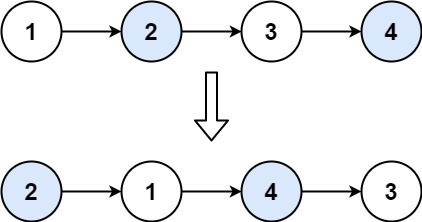
输入：head = [1,2,3,4]
输出：[2,1,4,3]

 使用一个虚拟头结点以便于最后确认头结点的位置，交换操作按一组一组来进行，注意链表大小为奇数时退出while的条件会改变：

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode* newhead = new ListNode(0);
        newhead->next = head;
        ListNode*cur = newhead;
        // cur->next != NULL处理size为偶数的链表，cur->next->next != NULL处理的是size为奇数的链表
        while(cur->next != NULL && cur->next->next != NULL){
            ListNode* tmp1 = cur->next;
            ListNode* tmp2 = cur->next->next->next;
            cur->next = cur->next->next;    //步骤一
            cur->next->next = tmp1;         //步骤二
            tmp1->next = tmp2;              //步骤三
            cur = cur->next->next;
        }
        head = newhead->next;
        delete newhead;
        return head;
    }
};

结合双指针

19：删除链表的倒数第N个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

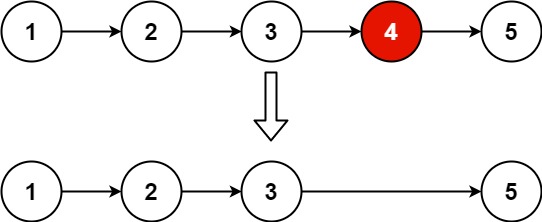
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

结合快慢指针的思想一个快的负责遍历整个链表，一个慢指针找导数第n个节点：

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* newhead = new ListNode(0);
        newhead->next = head;
        ListNode* f = newhead;
        ListNode* s = newhead;
        while(n--){
            f = f->next;
        }
        while(f->next != NULL){
          f = f->next;
          s = s->next;
        }
        ListNode* tmp = s->next;
        s->next = s->next->next;
        delete tmp;
        head = newhead->next;
        return head;
    }
};

160:相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

根据长度是否相同我们可以采取比较“共同长度的公共子链表部分”，也就是先移动长链表的指针到公共子链的起始节点，然后逐步后移比较两指针是否相同：

class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        int size_A = 0, size_B = 0;
        int count = 0;
        ListNode* cur_A = headA;
        ListNode* cur_B = headB;
        while(cur_A->next != NULL){
            size_A++;
            cur_A = cur_A->next;
        }
        size_A++;
        cur_A = headA;
        while(cur_B->next != NULL){
            size_B++;
            cur_B = cur_B->next;
        }
        size_B++;
        cur_B = headB;
        count = abs(size_A - size_B);
        if(size_A >= size_B){
            while(count--){
                cur_A = cur_A->next;
            }
            while(cur_A != cur_B){
                cur_A = cur_A->next;
                cur_B = cur_B->next;
            }
            if(cur_A == cur_B){
                return cur_A;
            }else{
                return NULL;
            }
        }else{
            while(count--){
                cur_B = cur_B->next;
            }
            while(cur_A != cur_B){
                cur_A = cur_A->next;
                cur_B = cur_B->next;
            }
            if(cur_A == cur_B){
                return cur_B;
            }else{
                return NULL;
            }
        }
    }
};

142：环形链表II

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

一、判断链表中是否有环？

使用快慢指针，通过设置不同的速度（步长）来确保两指针在有环的情况下会发生相遇。

 二、找到进入环的节点：

通过途中我们可以得到在第一次相遇是快指针已经比慢指针多走了n圈 ，根据两者速度得到的整体路程的关系可以得到等式：

2 * (x + y) = x + y + n(z +y)

通过简单变形将x单拿出来，并将z单拿出来可以得到：

x = z + (n - 1)(z + y)

从而我们就可以获取到从第一次相遇之后走到环入口的距离就是从头结点走到换入口的距离，我们设置一个指针同时从头结点和相遇节点向前走直到相遇，相遇的节点就是环的入口。

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow = head;
        ListNode* fast = head;
        ListNode* res = head;
        while(fast != NULL && fast->next != NULL){
            fast = fast->next->next;
            slow = slow->next;
            if(fast == slow){
                ListNode* tmp = fast;
                while(res != tmp){
                    res = res->next;
                    tmp = tmp->next;
                }
                return res;
            }
        } 
        return NULL;
    }
};