🌟 嗨，我是Lethehong！🌟
🌍 立志在坚不欲说，成功在久不在速🌍
🚀 欢迎关注：👍点赞⬆️留言收藏🚀
🍀欢迎使用：小智初学计算机网页AI🍀
目录
一、数组的基本概念
数组的特点是每个数据元素可以又是一个线性表结构。因此，数组结构可以简单地定义为：若线性表中的数据元素为非结构的简单元素，则称为一维数组，即为向量；若一维数组中的数据元素又是一维数组结构，则称为二维数组；依次类推，若二维数组中的元素又是一个一维数组结构，则称作三维数组。
结论：线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展。
举例：
其中，A 是数组结构的名称，整个数组元素可以看成是由 m 个行向量和 n 个列向量组成，其元素总数为 m×n。在 C 语言中，二维数组中的数据元素可以表示成 a[表达式1][表达式 2]，表达式 1 和表达式 2 被称为下标表达式，比如，a[i][j]。
数组结构在创建时就确定了组成该结构的行向量数目和列向量数目，因此，在数组结构中不存在插入、删除元素的操作。
二、数组的表示方法
（1）一维数组
从理论上讲，数组结构也可以使用两种存储结构，即顺序存储结构和链式存储结构。然而，由于数组结构没有插入、删除元素的操作，所以使用顺序存储结构更为适宜。换句话说，一般的数组结构不使用链式存储结构。
组成数组结构的元素可以是多维的，但存储数据元素的内存单元地址是一维的，因此，在存储数组结构之前，需要解决将多维关系映射到一维关系的问题。举例：
LOC(i,j)=LOC(0,0)+(n*i+j)*L
数组结构的定义：
#define MAX_ROW_INDEX 10
#define MAX_COL_INDEX
10
typedef struct {
EnterType item[MAX_ROW_INDEX][MAX_COL_INDEX] ;
} ARRAY;（2）二维数组
二维数组就是平常所说的矩阵，也可以看成是数据元素是一维数组的一位数组。由于计算机内部存储器的地址是一维线性排列的，故在存储数据时，必须将二维数组转换为计算机的内部存储形式才可以。一般有两种存储方式：以行为主的存储方式（row-major）和以列为主的存储方式（column-major）。
设二维数组 A[1:U1
,1:U
2
]，该数组有（U
1
－1）＋1＝U
1
行，有（U
1
－1）＋1＝U
1
列。设每个元素占 d 个空间，数组的起始地址为 L1
。
① 以行为主（row-major）：
也称行优先存储，
其特点为：以每行为单位，一行一行的放入内存，如 C 语言、PASCAL 语言等都是如此处理二维数组的。
二维数组 A 可以看成有 U
1
个一维数组组成，每个一维数组有 U
2
个元素。如上图：
二维数组的行优先存储
由上图可得
- 第 i 行数据元素的起始地址为：(i-1) ×U2×d ＋ L1
- 数组元素 A[i,j]的地址为：Loc(A[i,j]) = L1 + (i-1)×U2 ×d ＋ （j－1）×d
② 以列为主（column-major）：
也称列优先存储，
特点为：以每列为单位，一列一列的放入内存，如 Fortran 语言就是如此处理二维数组的。二维数组 A 可以看成有 U2个一维数组组成，每个一维数组有 U1个元素。
同（1）类似，有：
- 第 j 列数据元素的起始地址为：(j-1) ×U1×d ＋ L1
- 数组元素 A[i,j]的地址为：Loc(A[i,j]) = L1 + (j-1)×U1×d ＋ （i－1）×d
重要说明：
二维数组 Am*n
的含义是：该数组有 m 行（0~m-1 第一维），有 n 列（0~n-1，第二维），占用 m*n 个存储空间。假设每个数据元素占用 L 个存储单元（可理解为字节），则二维数组 A 中任意一个元素 aij
的存储位置为：
行优先： LOC(i，j) ＝ LOC(0,0) ＋ （n×i＋j）×L
列优先： LOC(i，j) ＝ LOC(0,0) ＋ （m×j＋i）×L
二维数组是一种随机存储结构，因为存取数组中任一元素的时间都相等（单链表则不是，因为需要顺链访问，访问时间同数据元素的存储位置有关）。
三、特殊矩阵
所谓特殊矩阵就是元素值的排列具有一定规律的矩阵。常见的这类矩阵有：
对称矩阵、下（上）三角矩阵、对角线矩阵
等等。
对称矩阵的特点是 aij=aji
，比如，下面就是一个对称矩阵：
下（上）三角矩阵的特点是以主对角线为界的上（下）半部分是一个固定的值，下（上）半部分的元素值没有任何规律。
比如，下面是一个下三角矩阵：
对角矩阵的特点是所有的非零元素都集中在以主对角线为中心的带状区域中。
比如，下面就是一个 3 阶对角矩阵：
对于这些特殊矩阵，应该充分利用元素值的分布规律，将其进行压缩存储。
选择压缩存储的方法应
遵循两条原则
：一是尽可能地压缩数据量，二是压缩后仍然可以比较容易地进行各项基本操作。
三种特殊矩阵的压缩方法：
（1）对称矩阵
对称矩阵的特点是 aij
=a
ji
。一个 n×n 的方阵，共有 n
2
个元素，而实际上在对称矩阵中有 n(n-1)/2 个元素可以通过其他元素获得。
压缩的方法是首先将二维关系映射成一维关系，并只存储其中必要的 n(n+1)/2 个（主对角线和下三角）元素内容，这些元素的存储顺序以行为主序。举例：
假设定义一个数组型变量：int A[10];
k 是对称矩阵位于（i，j）位置的元素在一维数组中的存放位置。
操作算法的实现：
int Value(int A[],EntryType *item,int i,int j)
{
if (i<1||i>MAX_ROW_INDEX|| j<1||j>MAX_COL_INDEX) return FALSE;
else {
if (i>=j) k=i*(i-1)/2+j-1;
else k=j*(j-1)/2+i-1;
*item=A[k];
return TRUE;
}
}（2）下（上）三角矩阵
下三角矩阵的压缩存储与上面讲述的对称矩阵的压缩存储一样，只是将上三角部分的常量值存储在 0 单元，下三角和主对角上的元素从 1 号单元开始存放。
举例：
对于任意的（i，j），在一维数组中的存放位置可利用下列公式求得：
操作算法的实现：
int Value(int A[],EntryType *item,int i,int j)
{
if (i<1||i>MAX_ROW_INDEX||j<1||j>MAX_COL_INDEX) return FALSE;
else { if (i>=j) k=i*(i-1)/2+j;
else k=0;
*item=A[k];
return TRUE;
}
}（3）对角矩阵
我们以三阶对角矩阵为例讨论一下它的压缩存储方法。对于对角矩阵，压缩存储的主要思路是只存储非零元素。这些非零元素按以行为主序的顺序，从下标为 1 的位置开始依次存放在一维数组中，而 0 位置存放数值 0。
下面我们讨论一下对于任意给定的（i，j），求得在一维数组中存储位置 k 的方法。
操作算法的实现：
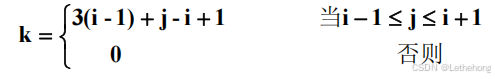
int Value(int A[ ],EntryType *item,int i,int j)
{
if (i<1||i>MAX_ROW_INDEX||j<1||j>MAX_COL_INDEX) return FALSE;
else { if (j>=(i-1)&&j<=(i+1)) k=3*(i-1)+j-i+1;
else k=0;
*item=A[k];
return TRUE;
}
}四、稀疏矩阵的压缩存储
① 定义
如果某个矩阵中的元素取值大部分都为零，只有少部分不为零，称这样的矩阵为稀疏矩阵。稀疏矩阵是一个笼统的概念，没有精确的定义，一般可认为当稀疏因子δ<=0.05 (非零元素占总元素数的百分比) 时就是稀疏矩阵。以下矩阵可认为是一个稀疏矩阵：
② 三种压缩存储方式
- 三元组顺序表
稀疏矩阵可采用压缩存储，仅存储其中的非零元素。存储时，除了记下非零元素的值外，还要记录其行标 i 和列标 j，即用（i,j,aij）三元组表示。由此可得出如下结论：稀疏矩阵可由表示非零元素的三元组及其行、列数唯一确定。
三元组结构：
typedef struct {
int i ,j ; //行标和列标
ElemType e ; //元素值
} Triple ;
typedef struct {
Triple data[MAXSIZE +1] ; //从 Data[1]开始使用，Data[0]不用
Int mu, nu,tu ; //矩阵的行数，列数及非零元素个数
}TSMatrix ;
举例：利用稀疏矩阵的三元组结构求矩阵 M 的转置矩阵 T。关键代码如下：
T.mu = M.nu ; T.u = M.mu ; T.tu = M.tu ;//转置后行数变为列数，列数变为行数，非零元个数不变
If (T.tu) {
q=1 ;//从三元组的第一个开始使用，第 0 个不用；
for ( col = 1 ; col <= M.nu ; ++col) //从 M 的第一列开始查找
for (p=1 ; p <= M.tu ; ++p)//从三元组的第一个元素开始查询
if (M.data[p].j == col) //如果某第 P 个三元组元素的列表同 col 相同，则转置
{ T.data[q].i = M.data[p].j ;
T.data[q].j = M.data[p].i ;
T.data[q].e = M.data[p].e ;
++q ;
}
} ;
说明：从上面的算法可以看出，对 M 中的每一列，都要遍历一次三元组的所有元素，找出其中属于该列的所有非零元。由于 M 中三元组的排列是按照先行有序、再列有序的原则存储的，因此通过上述方法转置后，在 T 中一定可以得到先列有序，再行有序的三元组来。
- 行逻辑链接的顺序表：
重新定义稀疏矩阵类如下:
class RLSMatrix {
private:
Array<Triple> data;
//非零元三元组表，
int mu, nu, tu;
// 矩阵的行数、列数和非零元个数39
Array<int> rpos;
// 矩阵中每一行的第一个非零元
// 在三元组表中的位序
…修改前述的稀疏矩阵的类定义，增加一个数据成员 rpos, 其值在稀疏矩阵的构造函数中确定。
矩阵乘法的经典算法:
for (i=1; i<=m1; ++i)
for (j=1; j<=n2; ++j) {
Q[i][j] = 0;
for (k=1; k<=n1; ++k) Q[i][j] += M[i][k] * N[k][j];
}
以上算法的时间复杂度为: O(m1×n1×n2)。以行逻辑联接的顺序表表示稀疏矩阵时，两个稀疏矩阵相乘（Q=M×
N）的过程可大致描述如下：
Q 初始化;
if Q 是非零矩阵 { // 逐行求积
for (arow=1; arow<=M.mu; ++arow) {
// 处理 M 的每一行
ctemp[] = 0;
// 累加器清零
计算 Q 中第 arow 行的积并存入 ctemp[]中；
将 ctemp[] 中非零元压缩存储到 Q.data 中；
} // for arow
} // if
RLSMatrix& RLSMarix::Product(const RLSMatrix& M, const RLSMatrix& N){
//求矩阵乘积 Q=M*N，采用行逻辑链接存储表示。
if (M.nu != N.mu) return ERROR;
sz = M.data.ListSize( );
RLSMatrix Q(M.mu, N.nu, 0, sz);// Q 初始化
if (M.tu*N.tu != 0) {// Q 是非零矩阵
for (arow=1; arow<=M.mu; ++arow) { // 处理 M 的每一行
ctemp[] = 0;// 当前行各元素累加器清零
Q.rpos[arow] = Q.tu+1;// 设置当前行第一个非零元在三元组表中的位序
for (p=M.rpos[arow]; p<M.rpos[arow+1]; ++p)
// 对当前行中每一个非零元
brow=M.data[p].j; // 找到对应元在 N 中的行号
if (brow < N.nu ) t = N.rpos[brow+1];40
else { t = N.tu+1 }
// t 指示该行中最后一个非零元的位置
for (q=N.rpos[brow]; q< t; ++q) {
ccol = N.data[q].j;// 乘积元素在 Q 中列号
ctemp[ccol] += M.data[p].e * N.data[q].e;
} // for q
} // 求得 Q 中第 crow( =arow)行的非零元
for (ccol=1; ccol<=Q.nu; ++ccol) // 压缩存储该行非零元
if (ctemp[ccol]) { // 该列元素为非零元
if (++Q.tu > Q.data.ListSize( ))
Q.data.Resize(Q.data.ListSize+Q.nu);
Q.data[Q.tu] = {arow, ccol, ctemp[ccol]};
} // if
} // for arow
} // if
return *Q;
} // Product- 十字链表
当矩阵的非零元个数和位置在操作过程中变化较大时，就不宜采用顺序存储结构来表示三元组的线性表。例如，在做“将矩阵 B 加到矩阵 A 上”的操作时，由于非零元的插入或删除将会引起 A.data 中元素的移动。为此，对这种类型的矩阵，采用链式存储结构表示三元组的线性表更为恰当。
在链表中，每个非零元可用一个含五个域的结点表示，其中 i, j 和 e 三个域分别表示该非零元所在的行、列和非零元的值，向右域 right 用以链接同一行中下一个非零元，向下域 down 用以链接同一列中下一个非零元。同一行的非零元通过 right域链接成一个线性链表，同一列的非零元通过 down 域链接成一个线性链表，每个非零元既是某个行链表中的一个结点，又是某个列链表中的一个结点，整个矩阵构成了一个十字交叉的链表，故称这样的存储结构为十字链表，可用两个分别存储行链表的头指针和列链表的头指针的一维数组表示之。例如：矩阵 M 的十字链表如下图所示。
五、广义表的基本概念
广义表是线性表的推广，广泛应用于人工智能等领域。一般记作：
LS＝ （a1,a2,…an）
a1 为表头，除去表头之外的其余元素组成的广义表为表尾，n 是广义表的长度。以上定义中：
表头为：a1，表尾为：(a2,a3,…,an) 。表尾也是一个广义表。
广义表的元素中，单个元素称为原子，如果元素也是一个广义表，则称这样的元素为子表。由此可见，广义表的定义是递归的。
例如:
D = (E, F)
E = (a, (b, c))
F = (d, (e))
A = ( )
B = (a, B) = (a, (a, (a, ... ,) ) )
C = (A, D, F)
六、广义表的结构特点
（1）广义表中的数据元素有相对次序；
（2）广义表的长度定义为最外层包含的元素个数; 广义表的深度定义为所含括弧的重数；
注意: “原子”的深度为“0”;“空表”的深度为 1；
（3）广义表可以共享；
（4）广义表可以是一个递归的表;递归表的深度是无穷值，长度是有限值。
（5）任何一个非空广义表 LS = ( a1, a
2, …,
a
n)均可分解为：
表头 Head(LS) = 1 和表尾 Tail(LS) = (
a
2, …,
a
n)两部分
例如：
LS = ( A, D )
Head(LS) = A，Tail(LS) = ( D )
Head( D ) = E，Tail( D ) = ( F )
Head( E ) = a ，Tail( E ) = ( ( b, c) )
Head( (( b, c)) ) = ( b, c) ，Tail( (( b, c)) ) = ( )
Head( ( b, c) ) = b ， Tail( ( b, c) ) = ( c )
Head( ( c ) ) = c ， Tail( ( c ) ) = ( )
七、广义表的抽象数据类型
（1）类型定义
假设有广义表 L
数据对象：D＝{ei | i=1,2,..,n; n≥0;
ei∈AtomSet 或 ei∈GList,
AtomSet 为某个数据对象 }
数据关系：LR＝{<ei-1, ei >| ei-1 ,ei ∈D, 2≤i≤n }
（2）广义表的基本操作：
- 结构的创建和销毁
InitGList(&L);
DestroyGList(&L);
CreateGList(&L, S);
CopyGList(&T, L);- 状态函数
GListLength(L);
GListDepth(L);
GListEmpty(L);
GetHead(L);
GetTail(L);- 插入和删除操作
InsertFirst_GL(&L, e);
DeleteFirst_GL(&L, &e);- 遍历
Traverse_GL(L, Visit());八、总结
本文详细介绍了数据结构中的数组与广义表的概念、表示方法和存储方式。首先，文章阐述了数组的基本概念，指出数组的特点是每个数据元素可以又是一个线性表结构，并说明了数组结构的定义和表示方法，包括一维数组和二维数组，以及数组的顺序存储结构。接着，文章讨论了特殊矩阵的压缩存储方法，包括对称矩阵、下（上）三角矩阵和对角矩阵，并给出了相应的压缩存储公式和操作算法。
文章进一步介绍了稀疏矩阵的压缩存储，包括三元组顺序表、行逻辑链接的顺序表和十字链表三种存储方式，并详细描述了稀疏矩阵乘法的算法。最后，文章阐述了广义表的基本概念、结构特点和抽象数据类型，包括广义表的类型定义、基本操作和状态函数。
总体来说，本文系统地讲解了数组与广义表的理论知识，并通过实例和算法介绍了它们在实际应用中的存储和操作方法。这些内容对于理解数据结构的基本原理和编程实现具有重要意义，为读者在后续学习过程中打下了坚实的基础。通过对本文的学习，读者可以更好地掌握数组与广义表的相关知识，为解决实际问题提供理论支持。同时，本文也为进一步研究数据结构的其他领域奠定了基础。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
