【蓝桥杯】学习记录——初入——动态规划算法学习

for(int i = 1;i <= m;i++)
    for(int j = 1;j <= n;j++)
        if(j >= w[i])
            dp[i][j] = max(dp[i-1][j],dp[i - 1][j - w[i]] + v[i]);   //如果背包容量较大，则允许装入物品v[i]后，总价值为之前计算的背包剩余容量对应的价值 + 此物品价值
        else
            dp[i][j] = dp[i-1][j]   //反之，则i行与上一行价值相同

可对上述二维解法优化，即将i维度折去，剩下j维度以此循环更新背包容量对应的价值。

所以，dp[m][n]即为maxValue。

一维解法：（将判断条件嵌入for循环）

for(int i = 1;i <= m;i++)
    for(int j = n;j >= w[i];j--)
            dp[j] = max(dp[j],dp[j - w[i]] + v[i]);   //如果背包容量较大，则允许装入物品v[i]后，总价值为之前计算的背包剩余容量对应的价值 + 此物品价值

此解法因为若背包容量较与w[i]小时，则对应数组保持不变，所以无须由if-else结构判断

但注意，j维度循环应该从右递减进行，因为此时才能保持物品不被重复拿取（前方背包容量对应价值还未被更新）

2.完全背包问题

特点：各类资源数都有无穷k个

例如：有一个容量位n的背包，周围有m种不同重量w的价格v不同的物品，每种物品有无穷k个数量，怎样尝试装入物品使背包中的总物品价值最大？

同样先讨论二维解法：

for(int i = 1;i <= m;i++)
    for(int j = 1;j <= n;j++){
        maxValue = 0;
        for(int k = 0;k * w[i] <= j; k++){    //尝试不同背包容量下对应可以放入多少数量相同物品并更新对应价值
            temp = dp[i - 1][j - k * w[i]] + k * v[i]);  
            if(temp > maxVlue) maxValue = temp;
        }
        dp[i][j] = maxValue;
    }

因为物品可重复拿取，参照之前叙述，所以j从左开始递增

一维解法：

for(int i = 1;i <= m;i++)
    for(int j = w[i];j <= n;j++){
        dp[j] = max(dp[j],dp[j - k * w[i]] + k * v[i]));  
    }

3.多重背包问题

特点：各类资源数都有有限量k个

例如：有一个容量位n的背包，周围有m种不同重量w的价格v不同的物品，每种物品有有限量k个数量，怎样尝试装入物品使背包中的总物品价值最大？

多重背包问题可拆解为01和完全背包问题分情况求解，而在我们不知有限量k的情况下考虑用对数级增长k模式进行价值更新，以减小时间复杂度。

void questionOne(int w,int v)   //01背包
{
    for(int j = n;j >= w;j--)
        dp[j] = max(dp[j],dp[j - w] + v);
}
void questionTwo(int w,int v)   //完全背包
{
    for(int j = w;j <= n;j++)
        dp[j] = max(dp[j],dp[j - w] + v);
}
void questiontThree(int w, int v,int k)   //多重背包
{
    if(k * w > n){      //用完全背包
        questionTwo(w,v);
        return;
    }
    else{
        int num = 1;
        while(num <= k){    //用01背包
            questionOne(k * w,k * v);
            k = k - num;      
            num << 1;        //指数级增长
        }
        if(k != 0) questionOne(K * w,k * v);   //k为某类物品最终剩余未计算量，所以将剩余物品拿取计算
    }
}

最终在主函数中套入for(int i = 1;i <= m;i++)循环即得结果dp[n]。

二、动态规划应注意事项及常见案例

1.内存优化

（1）斐波那契数列（f(n)=f(n-1)+f(n-2)）

为了避免重复计算——记录所计算的数据。

类似于跳台阶、铺瓷砖、填格子、字符串转换问题。

（2）递归注意栈溢出——数字三角形

注意数字三角形特征：i = j

1.从数据最后开始入手，将递归数据保存至新数组中——改成递推即可(从下往上)。

maxs[i][j] = max(maxs[i+1][j] + maxs[i+1][j+1]) + map[i+1][j+1]

2.从开始数据入手（从上往下）

maxs[i][j] = max(maxs[i-1][j-1] + maxs[i-1][j]) + map[i][j]

优化1：直接用数字三角形函数更新累加数据：

map[i][j] = max(map[i-1][j-1] + map[i-1][j]) + map[i][j]

优化2：将二维数据优化为一维数组（即用num[N]存储下一组数据值，lastNum[N]存储之前数据累加和，不断更新且num[]与lastNum[]相加）

注：用指针避免复制数组值，节约时间

3.动态规划之走格子问题等等

1.如果讨论从左上角的格子走到右下角的格子所用的（权值）路径最小，所以最小路径值是多少？

暴力解法太费事。

因为最左边和最上面的这两条路径时固定有的，记录这两条路径值后利用：

dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + dp[i][j] (即此格子的min(左边值，上边值）+此格子值)

所以求出每个格子的最小路径值直到求出右下角格子的最小路径值。

for(int i = 1;i <= n;i++)
    dp[1][i] = dp[1][i-1] + value[1][i];
for(int i = 1;i <= n;i++)
    dp[i][1] = dp[i-1][1] + value[i][1];
for(int i = 2;i <= n;i++)
    for(int j = 2;j <= n;j++)
            dp[i][j]  = min(dp[i][j-1],dp[i-1][j]) + value[i][j];

结果dp[n][m]即为结果

优化：将二维数组优化成一维（避免内存不足）

for(int i = 1;i <= m;i++){
    cin >> temp;
    dp[1][i] = dp[1][i-1] + temp;
}
for(int i = 2;i <= n;i++){
    cin >> temp;
    dp[1] += temp;            //从第2行开始的后几行的第一列的值单独提出来赋值
    for(int j = 2;j <= m;j++){
        cin >> temp;
        dp[j] = min(dp[j-1],dp[j]) + temp;
    }
}

在一维数组上进行实行的路径累加的更新。

结果即为dp[m]。

2.求走的路径方法总数

和上题方式相同，不过注意到最左和最上格子的路径都唯一，即都为1

同样此题可降维（与上题一样，只是无需输入）

3.格子刷油漆.

分类：（从顶点开始刷）,n列

one:每次把同一列刷完再刷下一列。方法数：a[i] = 2 * a[i-1]......2表示选取下一列的两个点。

two:每次刷的的列不同直到最后一列后返回，有去有回类型。方法数：b[i] = 2 * b[i-1]......2表示选取下一列的两个点。

three:刷一列然后刷下一列，然后返回刷上次未刷完的一列。方法数：a[i] = 2 * a[i-2] * 2......第一个2表示从顶点开始选取下两个点，第二个2表示从最后一个点开始选取下两个点。

总方法数为:a[i] = 2 * a[i - 1] + b[i] + 4 * a[i - 2]

（从中间点开始刷）

one:选取中间上点或下点，先遍历左部分，后遍历右部分。方法数：2 * b[i] * 2 * a[n - i]......第一个2表示上点或下点，第二个2表示选取G或F点

one:选取中间上点或下点，先遍历右部分，后遍历左部分。方法数：2 * b[n - i + 1] * 2 * a[i - 1]......第一个2表示上点或下点，第二个2表示选取C或D点

总方法数为:4 * (b[i] * a[n - i] + b[n - i + 1] * a[i - 1])

所以代码：

if(n == 1){
    cout << 2 << endl;
    return 0;
}
a[1] = 1,a[2] = 6;
b[1] = 1,b[2] = 2;
for(int i = 3;i <= n;i++){
    b[i] = 2 * b[i - 1];
    a[i] = 2 * a[i-1] + b[i] + 4 * a[i-2];
} 
//4个顶点
long long sum = 4 * a[n]; 
for(int i = 2;i < n;i++){
    sum += 4 * (b[i] * a[n-i] + b[n-i+1] * a[i-1]);
}

sum即为最终结果。

4.波动数列

关键：a和b默认为一个封闭组合、子集和的组合方式

详见过程。

void create(int n)
{
	dp[0]=1;
	for(int i=1;i<n;i++)
		for(int j=i*(i+1)/2;j>=i;j--)
			dp[j]=(dp[j]+dp[j-i])%MOD;	
}

int main()
{
	cin>>n>>s>>a>>b;
	int num=(n-1)*n/2;
	long long optnum=a+b;
	s += num*b;
	create(n);
	int ans=0;
	for(int i=0;i<=num;i++){
		long long temp=s-i*optnum;
		if(temp%n==0)
			ans=(ans+dp[i])%MOD;
	}
	cout<<ans<<endl;
	return 0;
}

5.求最大子序列之和

（1）前缀和求解（每次记录对应的最大值和最小值，maxSum即为max(prefix[i]-最小值)）

int minsum = 0x7fffffff,maxsum = 0x80000000;
for(int i = 1;i <= n;i++){
    cin >> num;
    prefix[i] = prefix[i-1] + num;
    minsum = min(minsum,prefix[i-1]);
    maxsum = max(maxsum,prefix[i] - minsum);
}    //maxsum即为结果

（2）动态规划求解(某段序列开始累加为负值，则代表此子序列最大值记录完毕，下次记录为下一子序列)

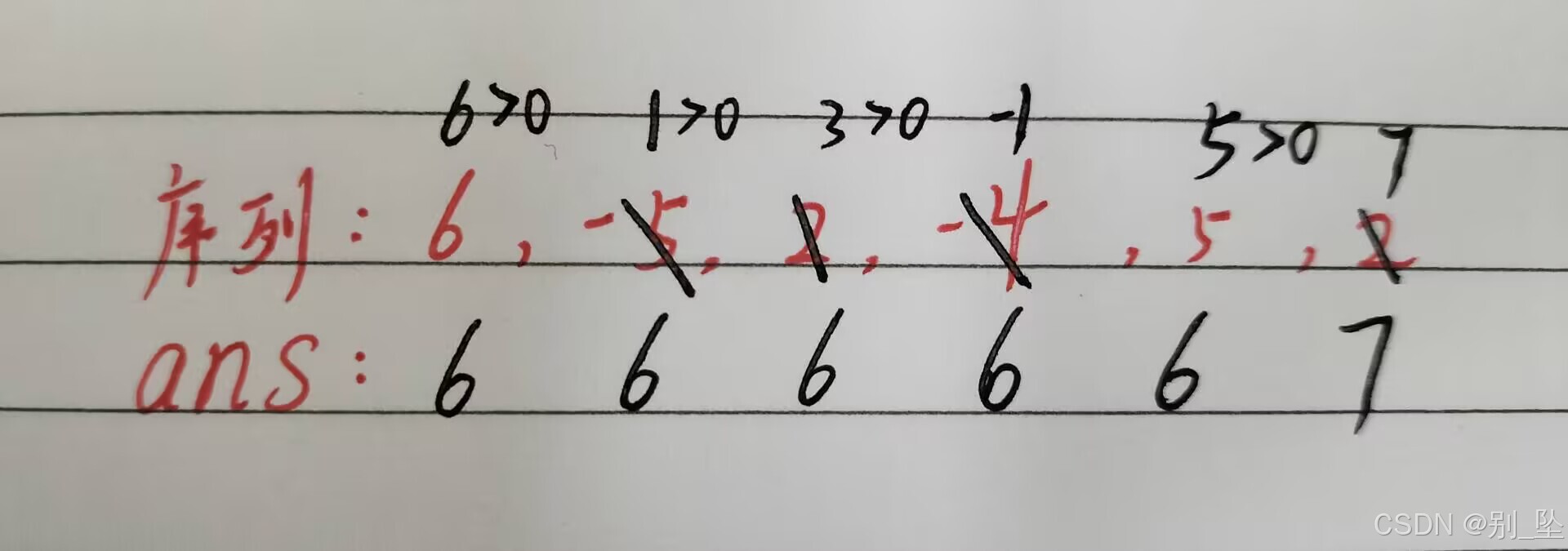
ina ans = dp[0];
for(int i = 1;i <= n;i++){
    if(dp[i - 1] >= 0) 
        dp[i] += dp[i - 1];
    ans = max(ans,dp[i]);
}

基于上述动态规划过程，可以简化，只用3个变量：

cin >> n >> sum;   //sum为输入序列的第一个值
max = sum;
while(--n){
    cin >> now;
    sum = sum > 0 ? sum : 0;
    sum += now;
    max = max > sum ? max : sum;
}
cout << max << endl;