中国剩余定理及其应用——解决复杂的同余问题

今天做第十三届蓝桥杯pythonB组的题的时候遇到了一个同余问题，题目如下：

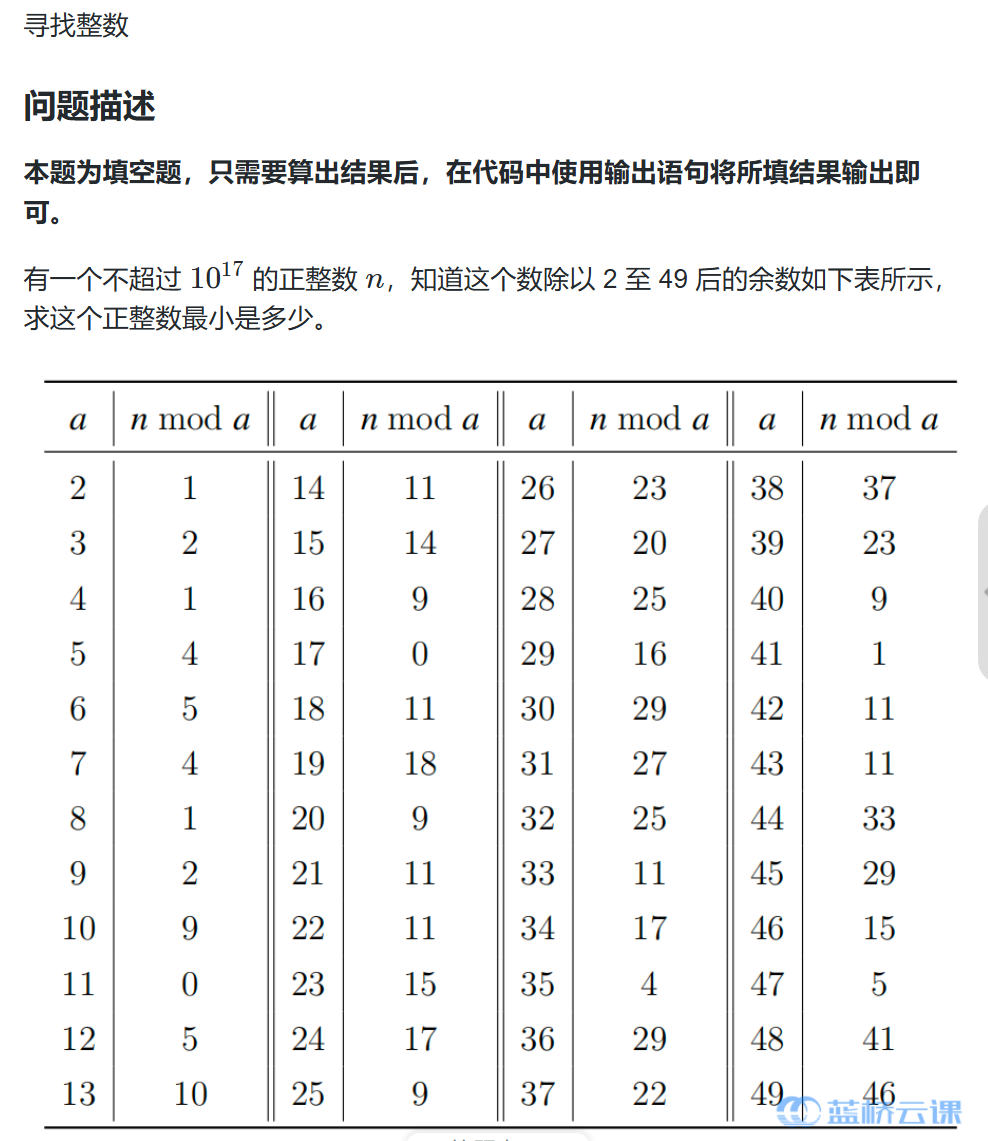
这道题的思路十分简单，直接暴力枚举就可以解决，所以我准备速战速决，但是敲代码的过程非常繁琐，只是在进行重复的工作，并且写好之后运行了将近10分钟还没有得到结果，可见计算量非常大，时间复杂度非常高，为了解决这个问题，我才用了新的方法中国剩余定理，详细介绍如下：
背景
中国剩余定理（Chinese Remainder Theorem, CRT）是一种数学工具，用于解决多个同余方程组的问题。它可以在满足一定条件下快速求解满足所有同余关系的最小正整数。

from sympy.ntheory.modular import solve_congruence

# 所有条件
conditions = [
    (0, 11), (0, 17),  # i % 11 == 0, i % 17 == 0
    (1, 2), (2, 3), (1, 4), (4, 5), (5, 6), (4, 7), (1, 8), (2, 9), (9, 10),
    (5, 12), (10, 13), (11, 14), (14, 15), (9, 16), (11, 18), (18, 19), (9, 20),
    (11, 21), (11, 22), (15, 23), (17, 24), (9, 25), (23, 26), (20, 27), (25, 28),
    (16, 29), (29, 30), (27, 31), (25, 32), (11, 33), (17, 34), (4, 35), (29, 36),
    (22, 37), (37, 38), (23, 39), (9, 40), (1, 41), (11, 42), (11, 43), (33, 44),
    (29, 45), (15, 46), (5, 47), (41, 48), (46, 49)
]

# 使用 solve_congruence 求解
solution, modulus = solve_congruence(*conditions)

# 输出结果
print("满足条件的最小整数:", solution)

很快便得到了结果2022040920220409，如果利用暴力搜索，甚至可能需要半个小时以上的时间
但是中国剩余定理明确提到模数需要两两互质，否则就要进行合并，但是我们的代码中却没有进行相关操作，原因是我们从sympy中调用的是拓展的CRT定理，该算法能够处理任意模数的系统，并且在模数有公因数时也能正确处理。