一、堆的概念
堆(Heap)是一种特殊的基于树的数据结构,通常分为最大堆和最小堆两种类型。它满足堆属性:对于最大堆,父节点的值总是大于或等于其子节点的值;而对于最小堆,父节点的值总是小于或等于其子节点的值。
数组实现:虽然堆是一个基于树的结构,但它通常用数组来实现。对于位于数组索引i处的元素,其左孩子的索引是2*i + 1,右孩子的索引是2*i + 2,而其父节点的索引是(i-1)/2
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质: 堆中某个节点(孩子节点)的值总是不大于或不小于其父节点的值;
堆总是一棵完全二叉树
2.堆得存储方式
二叉树层序遍历存储在数组中
1)堆的创建(大根堆)
向下调整法 (同理可创建小根堆,孩子中最小的与根节点交换)
完全二叉树从最后一棵子树慢慢调整为堆,最后一课子树根节点与左右孩子最大值交换(根节点<左/右孩子).然后记得递归调整堆结构被破坏的子树
package org.example;
import java.util.Arrays;
public class TestHeap {
private int[] elem;
private int usedsize;
public TestHeap(int capacity){
this.elem=new int[capacity];
}
//初始化堆
public void initHeap(int []array){
for (int i = 0; i < array.length ; i++) {
elem[i]=array[i];
usedsize++;//数组堆元素个数
}
}
public void display(){
System.out.println(Arrays.toString(elem));
}
//创建堆
//一棵子树有孩子一定先有左孩子 左孩子(usedsize-1-1)/2->父亲节点
public void createHeap(){
//从最后一棵子树根节点按个遍历每棵树根节点
for(int parent=((usedsize-1-1)/2);parent>=0;parent--){
shiftDown(parent,usedsize);
}
}
public void shiftDown(int parent,int usedsize){
int child=(2*parent)+1;//左孩子节点下标
while(child<usedsize){
//要确保有右孩子且不越界
if(child+1<usedsize&&elem[child]<elem[child+1]){
//右孩子比左孩子大 找到孩子节点的最大值
child++;
}
//child是左右孩子节点最大值的下标
if(elem[child]>elem[parent]){
//交换节点
swap(child,parent);
//父节点向下移,继续调整
parent=child;
child=2*parent+1;
}else {
//已经是大根堆不需要调整
break;
}
}
}
public void swap(int i,int j){
int tmp=elem[i];
elem[i]=elem[j];
elem[j]=tmp;
}
}
Test测试类
package org.example;
import java.util.Arrays;
public class Test {
public static void main(String[] args) {
int []array={27,15,19,18,28,34,65,49,25,37};
TestHeap testheap=new TestHeap(array.length);
testheap.initHeap(array);
testheap.createHeap();
testheap.display();
}
}
创建前
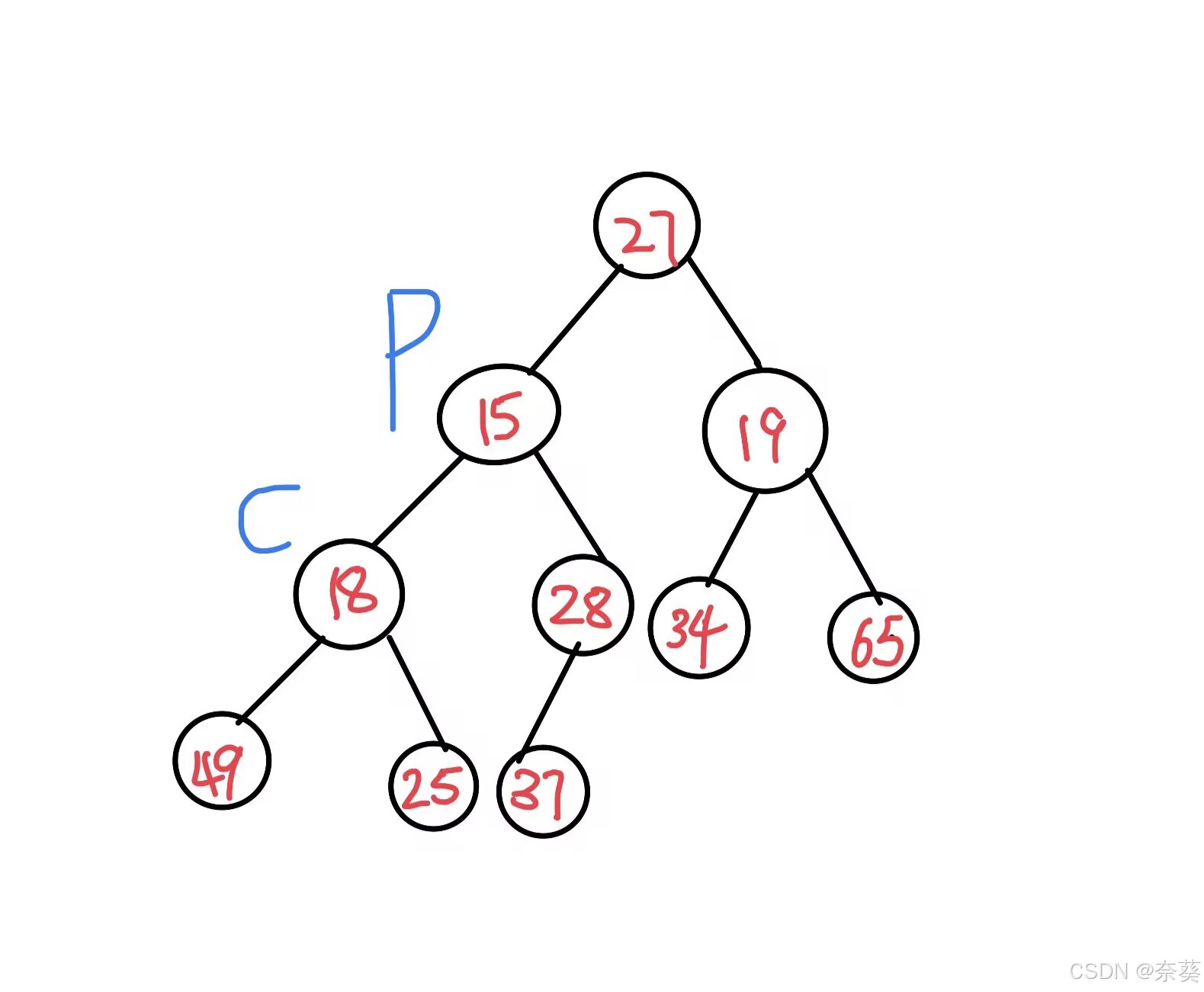
创建后(大根堆)
 2)堆的插入
2)堆的插入
向上调整(先将新插入的节点放到堆的末尾,最后一个孩子之后,堆的结构性质被破坏,在慢慢往上移,向上调整为大/小根堆)
注意:空间放满时需要扩容
public void offer(int val){
if(isfull()){
this.elem=Arrays.copyOf(elem,2*elem.length);
//向上调整
}
//添加的元素是新的孩子
this.elem[usedsize]=val;
shiftUp(usedsize);
usedsize++;
}
//向上调整函数 (也创建堆)
//向下调整方法比向上调整方法少遍历(最后)一层节点
public void shiftUp(int child){
int parent=(child-1)/2;
while (child>0){
if(elem[child]>elem[parent]){
swap(child,parent);
child=parent;
parent=(child-1)/2;
}else {
break;
}
}
}
public boolean isfull(){
return elem.length==usedsize;
}
main方法
int []array={27,15,19,18,28,34,65,49,25,37};
TestHeap testheap=new TestHeap(array.length);
testheap.initHeap(array);
testheap.createHeap();
//testheap.display();
testheap.offer(88);
//插入元素打印
testheap.display();
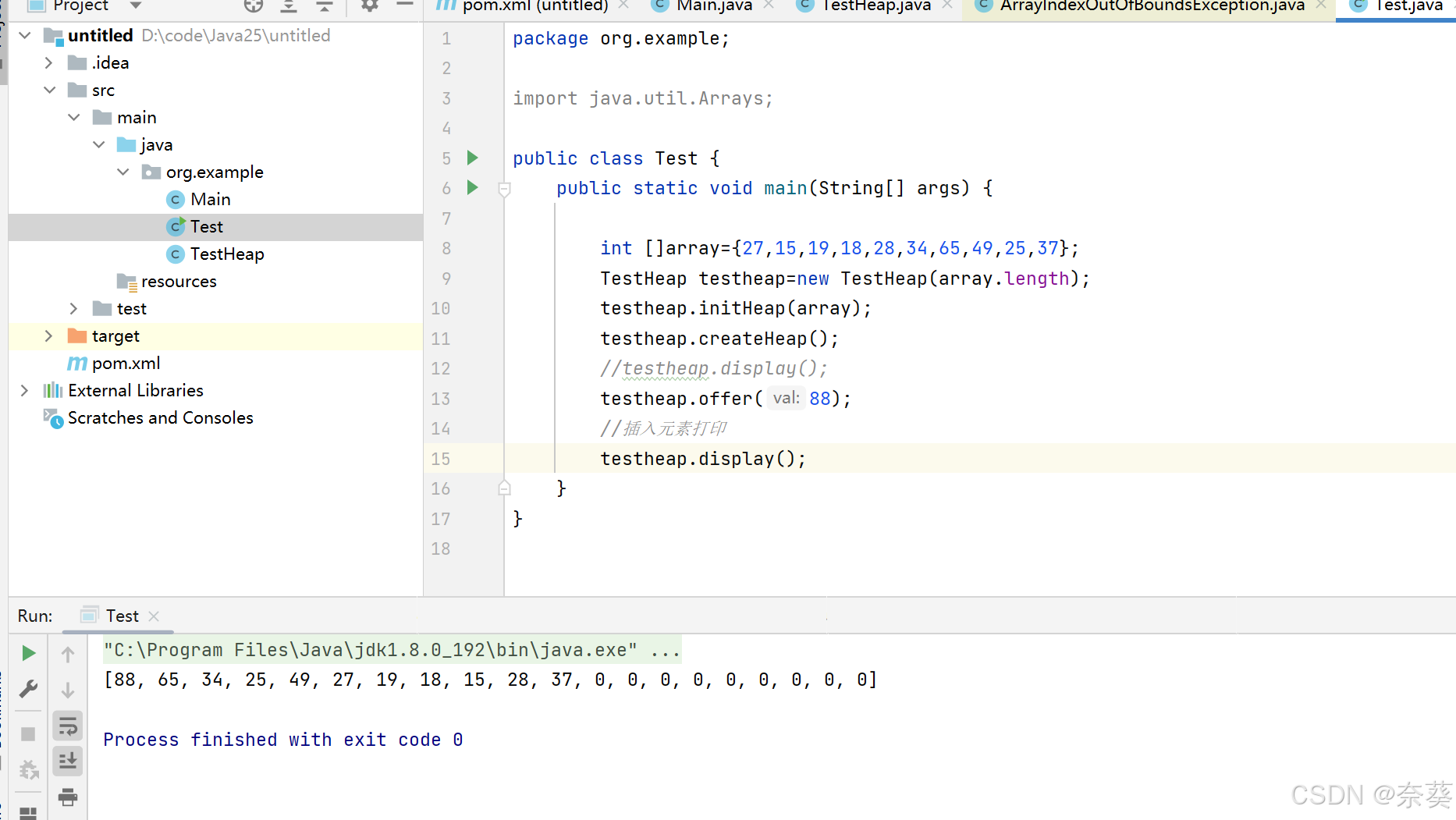
3)堆的删除
删除的一定是堆顶(根节点元素)
a.将堆顶元素与最后一个孩子元素交换
b.将堆中有效元素的个数减少一个
c.将堆顶元素向下调整,满足堆特性为止
public int pool(){
//一定是删除堆顶元素
int tmp= elem[0];//保留删除的元素
//交换元素
swap(0,usedsize-1);
usedsize--;
shiftDown(0,usedsize);
//返回被删除的元素
return tmp;
}
int val=testheap.pool();
System.out.println("被删除的元素是"+val);
//删除后元素打印
testheap.display();
public void display(){
// System.out.println(Arrays.toString(elem));
//显示堆的有效部分
System.out.println(Arrays.toString(Arrays.copyOf(elem, usedsize)));
}
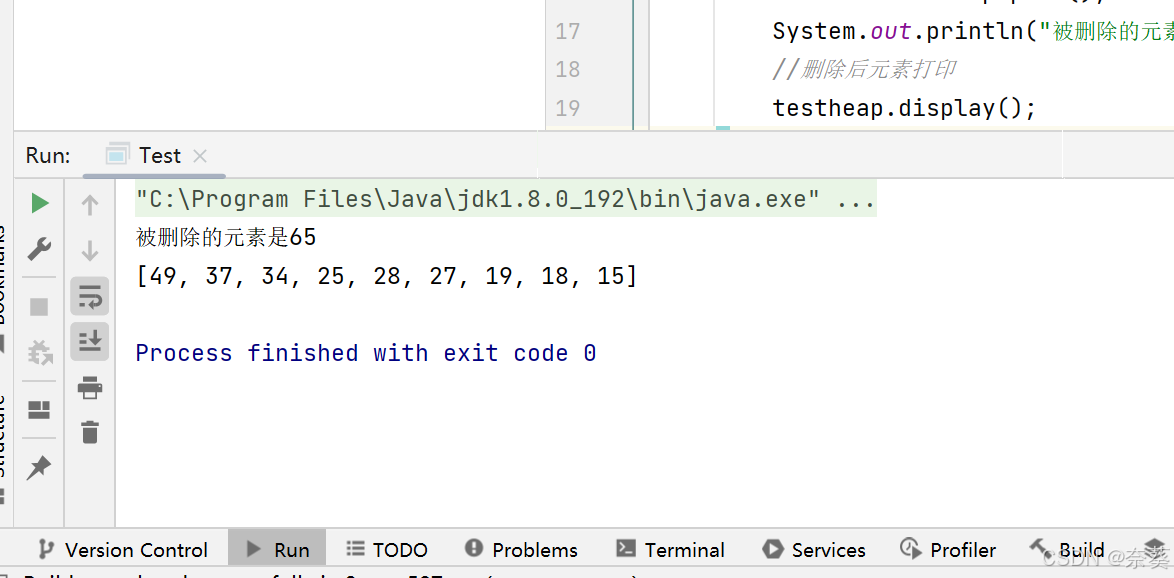
打印方法display()修改原因
你遇到的问题是:
> 删除堆顶元素(65)后,65 **仍然出现在数组中**,只是被“挤”到了最后面,数组并没有真正缩小,65 依然存在。
---
## ✅ 你的代码是**逻辑正确的**,但你对 `display()` 方法的理解有误。
---
## 🧠 堆的底层实现是一个数组,但它**不是动态收缩的数组**,而是通过 `usedsize` 来控制堆的有效元素数量。
你调用 `pool()` 方法后:
```java
usedsize--;
```
这意味着堆的有效长度减少了 1,但底层数组并没有变小,**只是堆不再“关心”最后一个元素**。
---
## 🔍 举个例子
你原来的堆是:
```
[65, 49, 34, 25, 37, 27, 19, 18, 15, 28]
```
调用 `pool()` 后,堆会执行:
```java
swap(0, usedsize - 1); // 交换 65 和 28
usedsize--; // usedsize 从 10 变成 9
shiftDown(0, usedsize); // 从新的堆顶 28 开始下滤
```
此时数组变成:
```
[49, 37, 34, 25, 28, 27, 19, 18, 15, 65]
```
但是 `usedsize = 9`,意味着堆只“看到”前 9 个元素:
```
[49, 37, 34, 25, 28, 27, 19, 18, 15]
```
而 `65` 被留在数组最后,**只是不再属于堆的范围**。
---
## ✅ 所以你看到的输出:
```
[49, 37, 34, 25, 28, 27, 19, 18, 15, 65]
```
这是完全正常的,因为:
- `display()` 方法打印的是整个数组(包括不属于堆的部分)
- 你没有重新拷贝数组或清空无效数据
---
## ✅ 如何正确打印堆的有效部分?
修改 `display()` 方法为只打印有效部分:
```java
public void display() {
System.out.println(Arrays.toString(Arrays.copyOf(elem, usedsize)));
}
```
## ✅ 修改后输出:
调用 `testheap.display();` 会输出:
```
49 37 34 25 28 27 19 18 15
```
二、优先级队列
队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队 列时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适,比如:在手机上玩游戏的时候,如 果有来电,那么系统应该优先处理打进来的电话;
数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。这种数 据结构就是优先级队列(Priority Queue)。
JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列,PriorityQueue是线 程不安全的,PriorityBlockingQueue是线程安全的
1)优先级队列使用
导包
import java.util.PriorityQueue;
2. PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出 ClassCastException异常
3. 不能插入null对象,否则会抛出NullPointerException
4. 没有容量限制,可以插入任意多个元素,其内部可以自动扩容
5. 插入和删除元素的时间复杂度为
6. PriorityQueue底层使用了堆数据结构
7. PriorityQueue默认情况下是小堆---即每次获取到的元素都是最小的元素
public class Test {
public static void main(String[] args) {
PriorityQueue<Integer> priorityQueue=new PriorityQueue<>();
priorityQueue.offer(10);
priorityQueue.offer(4);
priorityQueue.offer(8);
priorityQueue.offer(3);
priorityQueue.offer(7);
System.out.println(priorityQueue.poll());
System.out.println(priorityQueue.poll());
System.out.println(priorityQueue.poll());
System.out.println(priorityQueue.poll());
System.out.println(priorityQueue.poll());
}
打印结果证明是小根堆
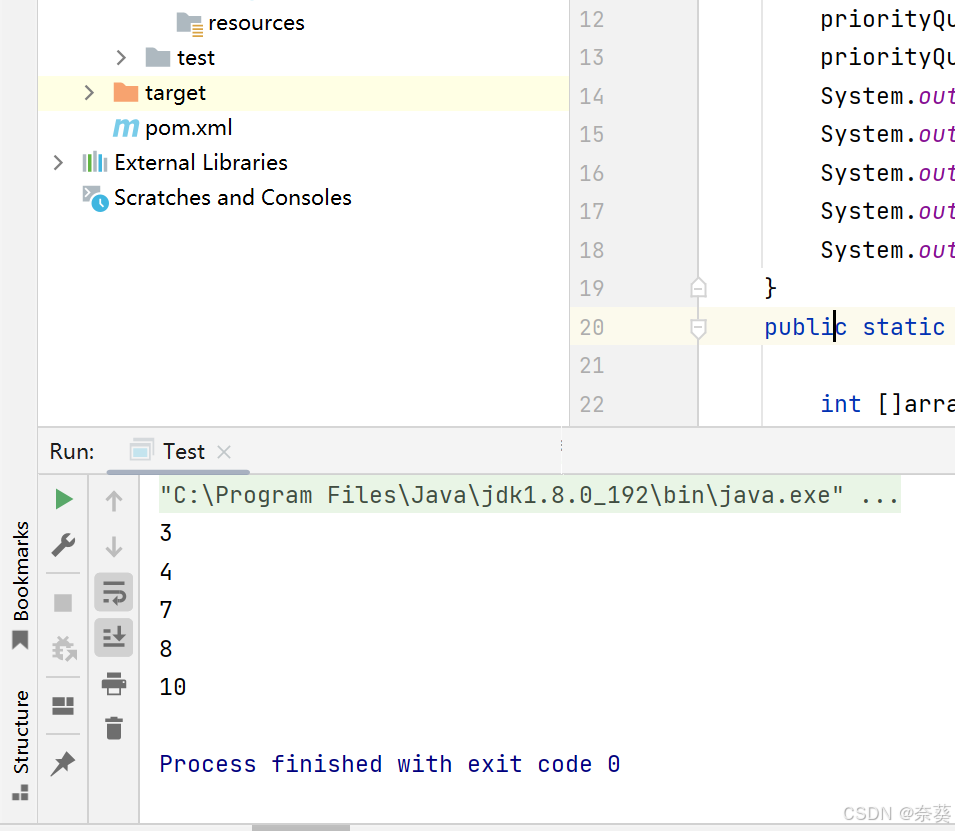
2)优先级队列的创建方式(3种)
static void TestPriorityQueue(){
// 创建一个空的优先级队列,底层默认容量是11
PriorityQueue<Integer> q1 = new PriorityQueue<>();
// 创建一个空的优先级队列,底层的容量为initialCapacity
PriorityQueue<Integer> q2 = new PriorityQueue<>(100);
ArrayList<Integer> list = new ArrayList<>();
list.add(4);
list.add(3);
list.add(2);
list.add(1);
// 用ArrayList对象来构造一个优先级队列的对象
// q3中已经包含了三个元素
PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
System.out.println(q3.size());
System.out.println(q3.peek());
}
3)优先级队列的使用方法
函数名 功能介绍
boolean offer(E e) 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时间复杂度 log2N,注意:空间不够时候会进行扩容
E peek() 获取优先级最高的元素,如果优先级队列为空,返回null
E poll() 移除优先级最高的元素并返回,如果优先级队列为空,返回null
int size() 获取有效元素的个数
void clear() 清空
boolean isEmpty() 检测优先级队列是否为空,空返回true




















 1918
1918

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








