一、项目
校园导游咨询
二、目的
(1)能够管理各参赛队的基本信息(包含参赛队编号,参赛作品名称,参赛学校,赛事类别,参赛者,指导老师),赛事类别共11项(参见大赛官网jsjds.blcu.edu.cn);包括增加、删除、修改参赛队伍的信息。
(2)从team.txt中读取参赛队伍的基本信息,实现基于二叉排序树的查找。根据提示输入参赛队编号,若查找成功,输出该赛事类别对应的基本信息(参赛作品名称、参赛学校、赛事类别、参赛者和指导老师信息),同时,输出查找成功时的平均查找长度ASL;否则,输出“查找失败!”。
(3)能够提供按参赛学校查询参赛团队(或根据赛事类别查询参赛团队),即,根据提示输入参赛学校名称(赛事类别),若查找成功,输出该学校参赛的(该赛事类别的)所有团队的基本信息,输出的参赛团队按赛事类别有序输出。(排序算法可从选择排序、插入排序、希尔排序、归并排序、堆排序中任意选择,并为选择算法的原因做出说明。)
(4)为省赛现场设计一个决赛叫号系统。所有参赛队按赛事组织文件中的赛事类别分到9个决赛室,决赛室按顺序叫号,被叫号参赛队进场,比赛结束后,下一参赛队才能进赛场。请模拟决赛叫号系统,演示省赛现场各决赛室的参赛队进场情况。(模拟时,要能直观展示叫号顺序与进场秩序一致)
(5)赛事系统为参赛者提供赛地的校园导游程序,为参赛者提供各种路径导航的查询服务。以我校长山校区提供比赛场地为例,(请为参赛者提供不少于10个目标地的导航。可为参赛者提供校园地图中任意目标地(建筑物)相关信息的查询;提供任意两个目标地(建筑物)的导航查询,即查询任意两个目的地(建筑物)之间的一条最短路径。
三、设计要求
1、赛事数据要求存入文件(txt或excel)并能读入查询;
2、赛地目的地查询,需提供目的地(建筑物)名称、代号、简介、两地之间路径长度等信息;
3、输入数据形式和范围:赛事相关数据可从键盘输入,或自文件导入。
4、界面要求:交互设计要合理,每个功能可以设计菜单,用户根据提示,完成相关功能的要求。
四、测试数据
以江苏科技大学长山校区为例,图例如下:
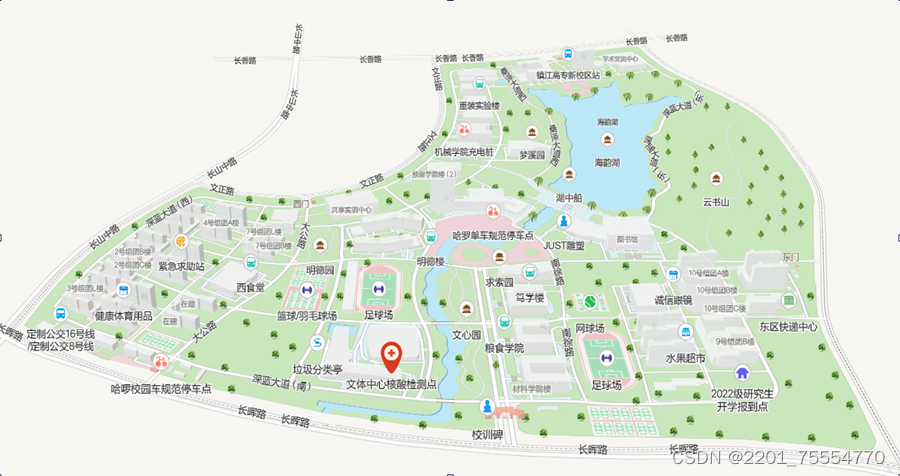
1.参赛队伍管理
从team.txt中读取参赛队伍的基本信息,能够管理各参赛队的基本信息(包含参赛队编号,参赛作品名称,参赛学校,赛事类别,参赛者,指导老师),赛事类别共11项(参见大赛官网jsjds.blcu.edu.cn);包括增加、删除、修改参赛队伍的信息。
- 1问题分析
使用指针来实现二叉排序树的存储。每个结点都是一个TreeNode结构体,其中包含了队伍信息和指向左右子节点的指针。根节点root是一个指向树的根结点的指针。
通过使用指针来连接各个结点,可以实现动态的插入,删除,修改等操作,并且可以根据结点之间的指针关系进行遍历和搜索。指针的使用使得二叉排序树可以高效地进行各种操作。
除了指针,队伍信息的存储使用了结构体TeamInfo,它包含了参赛队伍的各种信息,例如队伍编号、作品名称、学校、赛事类别、参赛者和指导老师。
1.2算法设计
增加参赛队伍信息
insert 函数:递归地插入新的节点到二叉排序树中。根据新节点的队伍编号与当前节点的队伍编号进行比较,决定将新节点插入左子树或右子树中。插入完成后,更新节点的高度,并进行平衡调整操作BSTNode 函数:对 insert 函数的包装,从根节点开始调用 insert 插入新的参赛队伍信息。BSTNode 函数:接收用户输入的参赛队伍信息,调用 BSTNode 函数将队伍信息插入二叉排序树中。
删除参赛队伍信息
remove 函数:递归地删除指定队伍编号的节点,并进行平衡调整。根据指定的队伍编号与当前节点的队伍编号进行比较,决定向左子树或右子树递归删除节点。若找到要删除的节点后,根据节点的子节点情况进行删除操作。若节点为叶子节点,直接删除;若节点只有一个子树,用子树代替当前节点;若节点有两个子树,找到右子树中的最小节点,将其值替换到当前节点,并递归删除最小节点。完成删除后,更新节点的高度,并进行平衡调整。successorParent函数:接收用户输入的要删除的参赛队伍编号,调用 successorParent 函数从二叉排序树中删除对应的队伍信息。
修改参赛队伍信息
modify 函数:通过递归查找二叉排序树中指定队伍编号的节点。从根节点开始,将指定队伍编号与当前节点的队伍编号进行比较,根据比较结果选择向左子树或右子树递归查找,直到找到匹配的节点或遍历到叶子节点为止。
1.3算法实现
// 插入节点
void BST::insert(Team data) {
BSTNode* node = new BSTNode();
node->data = data;
node->left = NULL;
node->right = NULL;
if (root == NULL) {
root = node;
}
else {
BSTNode* current = root;
while (true) {
if (data.id < current->data.id) {
if (current->left == NULL) {
current->left = node;
break;
}
else {
current = current->left;
}
}
else {
if (current->right == NULL) {
current->right = node;
break;
}
else {
current = current->right;
}
}
}
}
}
// 删除节点
void BST::remove(string id) {
BSTNode* parent = NULL;
BSTNode* current = root;
while (current != NULL && current->data.id != id) {
parent = current;
if (id < current->data.id) {
current = current->left;
}
else {
current = current->right;
}
}
if (current == NULL) {
return;
}
if (current->left == NULL) {
if (parent == NULL) {
root = current->right;
}
else {
if (current == parent->left) {
parent->left = current->right;
}
else {
parent->right = current->right;
}
}
delete current;
}
else if (current->right == NULL) {
if (parent == NULL) {
root = current->left;
}
else {
if (current == parent->left) {
parent->left = current->left;
}
else {
parent->right = current->left;
}
}
delete current;
}
else {
BSTNode* successorParent = current;
BSTNode* successor = current->right;
while (successor->left != NULL) {
successorParent = successor;
successor = successor->left;
}
if (successorParent != current) {
successorParent->left = successor->right;
successor->right = current->right;
}
if (parent == NULL) {
root = successor;
}
else {
if (current == parent->left) {
parent->left = successor;
}
else {
parent->right = successor;
}
}
successor->left = current->left;
delete current;
}
}
// 修改节点
void BST::modify(string id, Team data) {
remove(id);
insert(data);
}
// 查找节点
BSTNode* BST::search(string id) {
BSTNode* current = root;
while (current != NULL && current->data.id != id) {
if (id < current->data.id) {
current = current->left;
}
else {
current = current->right;
}
}
return current;
}1.4实验结果
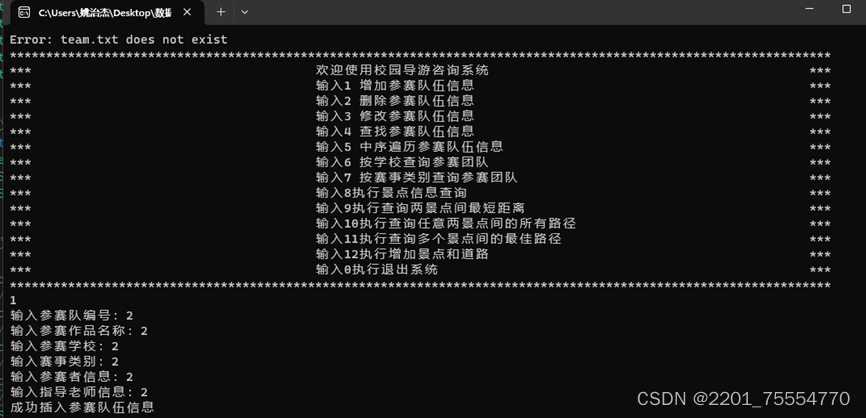
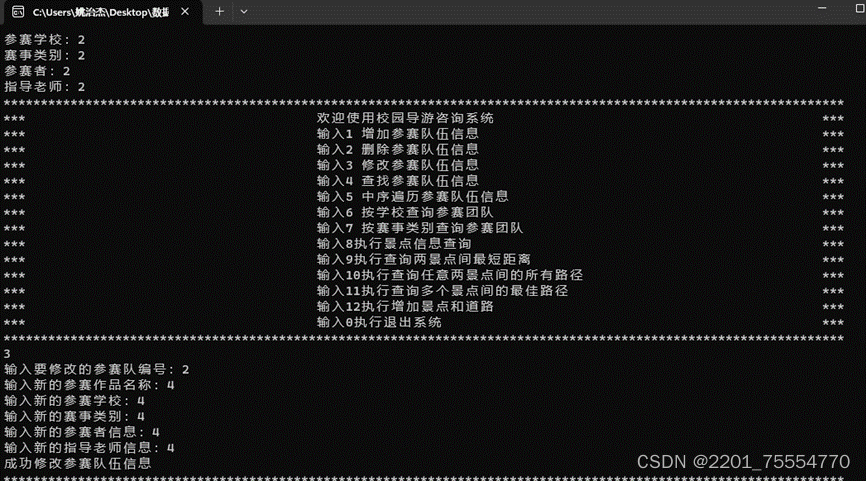
2.基于二叉排序树的查找
实现基于二叉排序树的查找。根据提示输入参赛队编号,若查找成功,输出该赛事类别对应的基本信息(参赛作品名称、参赛学校、赛事类别、参赛者和指导老师信息),同时,输出查找成功时的平均查找长度ASL;否则,输出“查找失败!”。请输出ASL的计算表达式和结果值。
问题分析
参赛队伍信息需要根据参赛队编号进行查询,并计算平均查找长度ASL,使用二叉排序树来存储参赛队伍信息。根节点指向树的根部,每个节点包含一个队伍信息对象,并根据队伍编号进行排序。左子节点的队伍编号小于父节点的队伍编号,右子节点的队伍编号大于父节点的队伍编号
- 1算法设计
参赛队伍信息查询模块需要实现以下操作:
1.根据参赛队编号查找相应的参赛队伍信息。
2。计算平均查找长度ASL。
height 函数:用于获取节点的高度。如果节点为空,则返回0;否则返回节点的高度。ASL 函数:用于计算二叉排序树的平均查找长度(ASL)。通过调用辅助函数calculateASLHelper 递归计算每个节点的层级,并累加到总的查找长度 totalASL 中。同时,记录节点的数量 nodeCount。最后,将总的查找长度除以节点数量得到平均查找长度。calculateASLHelper 函数:辅助函数,用于递归计算每个节点的层级。通过前序遍历二叉排序树,对每个非空节点,将当前层级 level 累加到总的查找长度 totalASL 中,并递归调用左子节点和右子节点进行层级计算。inorderTraversal函数:基于二叉排序树的中序遍历操作。用户输入要查找的参赛队编号,调用 BSTNodes函数在二叉排序树中查找匹配的节点。如果找到匹配的节点,则输出队伍信息和平均查找长度(ASL)的计算结果。如果未找到匹配的节点,则输出查找失败的提示信息。
2.2算法实现
// 中序遍历
void BST::inorderTraversal() {
vector<Team> teams;
inorderTraversal(root, teams);
for (Team team : teams) {
cout << "参赛队编号:" << team.id << endl;
cout << "参赛作品名称:" << team.name << endl;
cout << "参赛学校:" << team.school << endl;
cout << "赛事类别:" << team.category << endl;
cout << "参赛者:" << team.members << endl;
cout << "指导老师:" << team.instructor << endl << endl;
}
}
void BST::inorderTraversal(BSTNode* node, vector<Team>& teams) {
if (node != NULL) {
inorderTraversal(node->left, teams);
teams.push_back(node->data);
inorderTraversal(node->right, teams);
}
}// 计算子树高度
int BST::height(BSTNode* node) {
if (node == NULL) {
return 0;
}
else {
int leftHeight = height(node->left);
int rightHeight = height(node->right);
return max(leftHeight, rightHeight) + 1;
}
}
// 计算平均查找长度ASL
void BST::ASL(BSTNode* node, int depth, int& sum) {
if (node != NULL) {
ASL(node->left, depth + 1, sum);
sum += depth;
ASL(node->right, depth + 1, sum);
}
}
// 销毁子树
void BST::destroy(BSTNode* node) {
if (node != NULL) {
destroy(node->left);
destroy(node->right);
delete node;
}
}
// 读取team.txt文件,生成二叉排序树
void readTeams(BST& bst) {
ifstream file("team.txt");
if (!file) {
cerr << "Error: team.txt does not exist" << endl;
return;
}
string line;
while (getline(file, line)) {
Team team;
team.id = line.substr(0, 5);
team.name = line.substr(6, 30);
team.school = line.substr(37, 20);
team.category = line.substr(58, 2);
team.members = line.substr(61, 100);
team.instructor = line.substr(162, 20);
bst.insert(team);
}
file.close();
}
const int maxValue = 9999;
const int maxVertices = 100; // 最大顶点数
const int DefaultVertices = 20; // 默认顶点数
const int num = 20;
struct ver //顶点的结构体
{
char code;
string name;
string intro;
};2.3实验结果

3.参赛团队查询
能够提供按参赛学校查询参赛团队,根据提示输入参赛学校名称,若查找成功,输出该学校参赛的所有团队的基本信息,输出的参赛团队需有序输出(按参赛队编号)。(排序算法可从选择排序、插入排序、希尔排序、归并排序、堆排序中任意选择,并为选择算法的原因做出说明。)
- 1问题分析
参赛团队信息需要根据参赛学校名称进行查询,并需要按赛事类别有序输出,可以使来存储参赛队伍信息。使用了向量(vector)来存储队伍信息,通过遍历和选择排序来进行查找和排序操作。选择排序是一种简单但效率较低的排序算法,它的主要思想是每次从未排序的元素中选择最小(或最大)的元素,然后将其放置在已排序序列的末尾。选择排序被用于对匹配的队伍信息按队伍编号进行排序。虽然选择排序的时间复杂度为O(n^2),效率不如更高级的排序算法(如快速排序或归并排序),但在小规模数据集的情况下,选择排序是可以接受的。选择排序的实现相对简单,代码量较少,易于理解和实现。这段代码的主要目的是演示按学校查询参赛队伍信息的功能,而不是关注排序算法的性能。因此,选择排序作为一个简单的排序方法可以满足排序需求。
3.2算法设计
读取参赛队信息文件数据,根据参赛学校名称查找相应的参赛团队信息,并按赛事类别有序输出。query函数的作用是遍历给定的参赛队伍信息,找到与指定学校匹配的队伍信息,并按队伍编号进行排序后输出query函数主要用于读取存储参赛队伍信息的文件(team.txt),将每行数据解析为队伍信息的结构体,并将其存储在名为team1的向量中。然后,它会要求用户输入需要查找的学校名称,并调用searchBySchool函数来进行查询和输出。
3.3算法实现
// 按学校类别查询参赛团队
void BST::query(string keyword, bool searchBySchool) {
vector<BSTNode*> nodes = queryNodes(keyword, searchBySchool, root);
sort(nodes.begin(), nodes.end(), [](BSTNode* a, BSTNode* b) {
return a->data.category < b->data.category;
});
for (BSTNode* node : nodes) {
cout << "参赛队编号:" << node->data.id << endl;
cout << "参赛作品名称:" << node->data.name << endl;
cout << "参赛学校:" << node->data.school << endl;
cout << "赛事类别:" << node->data.category << endl;
cout << "参赛者:" << node->data.members << endl;
cout << "指导老师:" << node->data.instructor << endl << endl;
}
}
vector<BSTNode*> BST::queryNodes(string keyword, bool searchBySchool, BSTNode* node) {
vector<BSTNode*> nodes;
if (node != NULL) {
if ((searchBySchool && node->data.school == keyword) ||
(!searchBySchool && node->data.category == keyword)) {
nodes.push_back(node);
}
vector<BSTNode*> leftNodes = queryNodes(keyword, searchBySchool, node->left);
nodes.insert(nodes.end(), leftNodes.begin(), leftNodes.end());
vector<BSTNode*> rightNodes = queryNodes(keyword, searchBySchool, node->right);
nodes.insert(nodes.end(), rightNodes.begin(), rightNodes.end());
}
return nodes;
}3.4实验结果
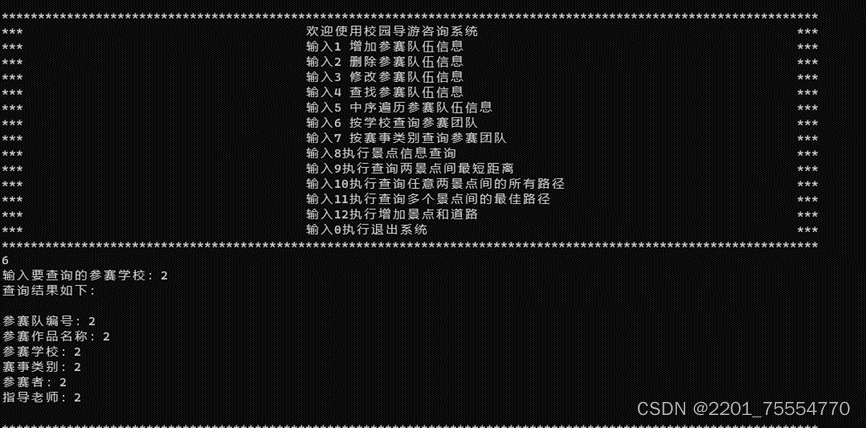
4.决赛叫号模拟
为省赛现场设计一个决赛叫号系统。所有参赛队按赛事组织文件中的赛事类别分到9个决赛室,决赛室按顺序叫号,被叫号参赛队进场,比赛结束后,下一参赛队才能进赛场。请模拟决赛叫号系统,演示省赛现场各决赛室的参赛队进场情况。(模拟时,各参赛队进场比赛时间可设为0.5秒)
- 1问题分析
决赛叫号需要模拟9个决赛室,每个决赛室可以有多个参赛队伍进行比赛,可以使用队列来存储参赛队伍信息。unordered_map<string, vector<TeamInfo>> categoryMap:使用无序映射(unordered_map),以赛事类别为键,将参赛队伍按照赛事类别分组存储。vector<string> categories:存储赛事类别,用于后续对赛事类别进行排序。vector<vector<TeamInfo>> finalRooms:二维向量,表示决赛室队伍的分配情况。每个决赛室作为一维向量,包含分配到该决赛室的参赛队伍。
4.2算法设计
遍历给定的参赛队伍信息,将参赛队伍按照赛事类别分组存储在categoryMap中,使用无序映射的特性,可以快速根据赛事类别查找对应的队伍信息。将赛事类别存储在categories向量中,并对其进行排序,以确保按照字典序输出。根据决赛室的数量,创建一个二维向量finalRooms,表示决赛室队伍的分配情况。依次遍历排好序的赛事类别categories,将每个赛事类别对应的队伍信息按顺序分配到决赛室中,通过取模运算实现循环分配。模拟决赛叫号的过程,依次输出每个决赛室的编号和其中的参赛队伍信息。在每个参赛队伍进入赛场后,使用this_thread::sleep_for函数模拟比赛结束前的等待时间。
4.3算法实现
// 决赛叫号系统
void finalsCallSystem(const vector<TeamInfo>& teamInfos) {
// 按照赛事类别将参赛队伍分组
unordered_map<string, vector<TeamInfo>> categoryMap;
for (const TeamInfo& info : teamInfos) {
categoryMap[info.eventCategory].push_back(info);
}
// 按照赛事类别进行排序
vector<string> categories;
for (const auto& pair : categoryMap) {
categories.push_back(pair.first);
}
sort(categories.begin(), categories.end());
// 将参赛队伍按照顺序分配到决赛室
int numFinalRooms = 9; // 决赛室数量
vector<vector<TeamInfo>> finalRooms(numFinalRooms); // 决赛室队伍
int roomIndex = 0;
for (const string& category : categories) {
const vector<TeamInfo>& teams = categoryMap[category];
for (const TeamInfo& team : teams) {
finalRooms[roomIndex].push_back(team);
roomIndex = (roomIndex + 1) % numFinalRooms;
}
}
// 模拟决赛叫号
for (int i = 0; i < numFinalRooms; i++) {
cout << "决赛室编号:" << i + 1 << endl;
cout << "=================" << endl;
const vector<TeamInfo>& teams = finalRooms[i];
for (const TeamInfo& team : teams) {
cout << "参赛队编号:" << team.teamNumber << " 进入赛场" << endl;
this_thread::sleep_for(chrono::milliseconds(500)); // 比赛结束前等待0.5秒
}
cout<< " 比赛结束" << endl;
cout << endl;
}
}
4.4实验结果
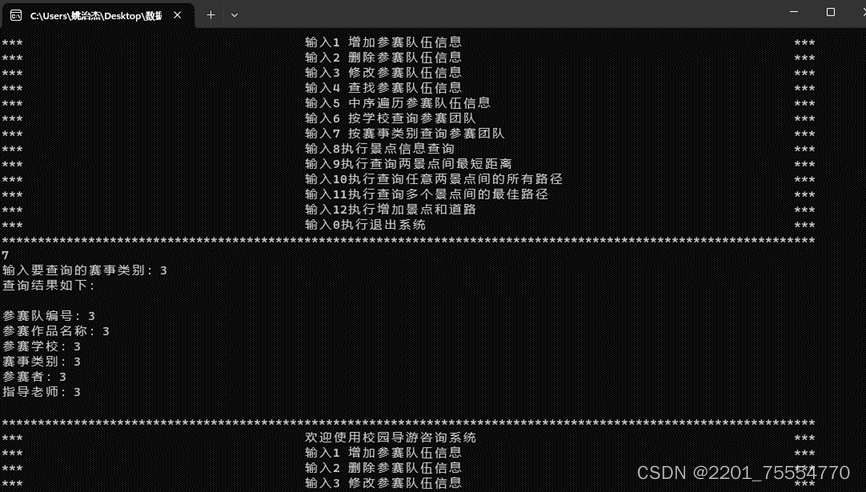
5.校园导航
赛事系统为参赛者提供赛地的校园导游程序。为参赛者提供各种路径导航的查询服务。以我校长山校区提供比赛场地为例,(请为参赛者提供不少于10个目标地的导航。可为参赛者提供校园地图中任意目标地(建筑物)相关信息的查询;提供图中任意目标地(建筑物)的问路查询,即查询任意两个目的地(建筑物)之间的一条最短的简单路径。
- 1问题分析
这显然是一个图论问题,而且校园内道路一般是双向通行的,所以这是一个无向图。对于图的存储结构而言,图中各个景点的存储结构有邻接表和邻接矩阵两种存储结构,考虑到顶点个数少于50个,所以邻接表和邻接矩阵的复杂度相同。本题中选择使用邻接矩阵来表示图。
5.2算法设计
读取校园地图信息文件和路径信息文件,构建图。根据参赛者的查询,提供相应的校园地图信息或路径导航查询服务。使用Dijkstra算法来计算起点到终点的最短路径。创建并初始化距离(distance)、前驱顶点(prev)和未访问顶点集合(unvisited)的数据结构。设置起点到起点的距离为0,将其他顶点的距离初始化为无穷大,并将起点加入未访问集合。在未访问集合中选择距离最小的顶点u,遍历u的邻居节点v,更新到v的距离和前驱顶点。重复上述步骤,直到终点被访问到或者所有顶点都被访问完。若终点的前驱顶点为-1,则表示无法找到最短路径,输出提示信息并返回。若存在最短路径,则通过前驱顶点记录的路径信息构建路径,并输出路径信息和长度。输出路径中每个目的地的详细信息。
5.3算法实现
class Graph //图的邻接矩阵类定义
{
public:
Graph(); // 构造函数
~Graph(); // 析构函数
int NumberOfVertices(); // 返回当前顶点数
int NumberOfEdges(); // 返回当前边数
ver getValue(int i); // 取顶点 i 的值
int getWeight(int v1, int v2); // 取边上权值
int getVertexPos(char code); // 给出顶点代码code在图中位置
bool insertVertex(char code, string name, string intro); // 插入一个顶点vertex
bool insertEdge(int v1, int v2, int cost); // 插入边(v1, v2), 权为cost
void Seek(int i); // 输出顶点i的信息
void ShortestPath(int v); // Dijkstra求最短路径算法
void CoutShortest(int v, int x); // 输出两顶点间的最短路径和距离
void FindAllPath(int** Array, Node startNodeKey, Node endNodeKey); // 查找两点间的所有路径
void CoutAllPath(int v1, int v2); // 输出两顶点间的所有路径
int FindManyPath(int v, int x); // 查找多个顶点间的最佳路径
void CoutMany(); // 输出多个顶点间的最佳路径
void Increase(); // 增加景点和道路
int** Edg() { return Edges; }; // 返回邻接矩阵
void search(); // 景点信息查询
void shorest(); // 查询两景点间最短距离
void allpath(); // 查询任意两景点间的所有路径
void Map(); // 动态生成景点列表
private:
int maxVertices; // 图中最大顶点数
int numEdges; // 当前边数
int numVertices; // 当前顶点数
ver* VerticesList; // 顶点表 (各边链表的头结点)
int** Edges; // 邻接矩阵保存边
int* path; // 保存该结点的前一个结点
int* dist; // 保存路径长度
int resultPath[num][num]; // 保存该结点的前一个结点
int result[num + 1]; // 保存结果集
bool Mark[num]; // 标记结点
int pathNum; // 两点间所有路径的数目
int nPos; // 栈中的顶点数
};
// 构造函数
Graph::Graph()
{
maxVertices = DefaultVertices; // 初始化 最大顶点数
numVertices = 0; // 初始化 顶点个数
numEdges = 0; // 初始化 边数
VerticesList = new ver[maxVertices]; // 创建顶点表数组
Edges = (int**) new int* [maxVertices]; // 创建邻接矩阵数组
for (int i = 0; i < maxVertices; i++)
Edges[i] = new int[maxVertices];
for (int i = 0; i < maxVertices; i++)
for (int j = 0; j < maxVertices; j++)
Edges[i][j] = (i == j) ? 0 : maxValue; // 邻接矩阵主对角线元素为0;顶点对间无边则权重无穷大
insertVertex('a', "三号组团", "三号组团为学生宿舍,由四栋并列的六层高楼组成。");
insertVertex('b', "西苑食堂", "位于学校西侧的学生食堂,分为三层,其中二楼为海洋船舶主题餐厅。");
insertVertex('c', "明德楼", "四栋教学楼之一。");
insertVertex('d', "文体中心", "学生进行体育课的地方,有乒乓球室、羽毛球室、飞镖房等。");
insertVertex('e', "西操场", "在文体中心对面,学生进行体育课的地方,旁边有网球场,轮滑场。");
insertVertex('f', "文理大楼", "江苏科技大学最高的楼,四栋教学楼之一,有着各种各样的教学设施。");
insertVertex('g', "北苑", "大部分学院的学院楼以及行政大楼所在地。");
insertVertex('h', "求索园", "绿荫小道,风景优美。");
insertVertex('i', "东苑食堂", "位于学校东侧的学生食堂。");
insertVertex('j', "图书馆", "拥有众多藏书以及学生自习的地方。");
insertEdge(0, 1, 100);
insertEdge(0, 3, 200);
insertEdge(1, 2, 80);
insertEdge(1, 3, 150);
insertEdge(2, 4, 120);
insertEdge(2, 5, 110);
insertEdge(3, 4, 50);
insertEdge(4, 7, 150);
insertEdge(4, 8, 230);
insertEdge(5, 6, 80);
insertEdge(5, 7, 60);
insertEdge(6, 9, 100);
insertEdge(7, 8, 90);
insertEdge(7, 9, 70);
insertEdge(8, 9, 50);
};
//析构函数
Graph::~Graph()
{
delete[] VerticesList;
delete[] Edges;
delete[] path;
delete[] dist;
};
//返回当前顶点数
int Graph::NumberOfVertices()
{
return numVertices;
};
//返回当前边数
int Graph::NumberOfEdges()
{
return numEdges;
};
// 取顶点 i 的值
ver Graph::getValue(int i)
{
return VerticesList[i];
};
// 取边上权值
int Graph::getWeight(int v1, int v2)
{
return Edges[v1][v2];
};
// 给出顶点代码code在图中位置
int Graph::getVertexPos(char code)
{
for (int i = 0; i < numVertices; i++)
if (VerticesList[i].code == code)
return i;
return -1;
};
// 插入一个顶点vertex
bool Graph::insertVertex(char code, string name, string intro)
{
if (numVertices == maxVertices)
return false;
VerticesList[numVertices].code = code;
VerticesList[numVertices].name = name;
VerticesList[numVertices].intro = intro;
numVertices++;
return true;
};
// 插入边(v1, v2), 权为cost
bool Graph::insertEdge(int v1, int v2, int weight)
{
if (v1 > -1 && v1<numVertices && v2>-1 && v2 < numVertices)
{
Edges[v1][v2] = Edges[v2][v1] = weight;
numEdges++;
return true;
}
else
return false;
};
// 输出顶点i的信息
void Graph::Seek(int i)
{
cout << "景点编号:" << VerticesList[i].code << endl;
cout << "景点名称:" << VerticesList[i].name << endl;
cout << "景点简介:" << VerticesList[i].intro << endl;
cout << "***************************************" << endl;
};
// 查询两景点之间的最短路径和距离
void Graph::ShortestPath(int v)
{
int n = NumberOfVertices();
dist = new int[n];
path = new int[n];
bool* S = new bool[n]; //最短路径顶点集
int i, j, k, w, min;
for (i = 0; i < n; i++)
{
dist[i] = getWeight(v, i); //数组初始化
S[i] = false;
if (i != v && dist[i] < maxValue)
path[i] = v;
else
path[i] = -1;
}
S[v] = true; //顶点v加入顶点集合
dist[v] = 0;
for (i = 0; i < n - 1; i++)
{
min = maxValue;
int u = v; //选不在S中具有最短路径的顶点u
for (j = 0; j < n; j++)
if (S[j] == false && dist[j] < min)
{
u = j;
min = dist[j];
}
S[u] = true; //顶点u加入集合S
for (k = 0; k < n; k++) //修改
{
w = getWeight(u, k);
if (S[k] == false && w < maxValue && dist[u] + w < dist[k]) //顶点k未加入S,且绕过u可以缩短路径
{
dist[k] = dist[u] + w;
path[k] = u; //修改到k的最短路径
}
}
}
};
//输出两景点之间的最短路径和距离
void Graph::CoutShortest(int v, int x)
{
int j, k, n;
n = NumberOfVertices();
int* d = new int[n];
{
j = x;
k = 0;
while (j != v)
{
d[k++] = j;
j = path[j];
}
cout << getValue(v).name << "到" << getValue(x).name << "的最短路径为:" << endl << getValue(v).name;
while (k > 0)
{
cout << "-->" << getValue(d[--k]).name;
}
cout << endl << "最短路径长度为:" << dist[x] << endl;
}
delete[] d;
};
//查找两点间的所有路径
void Graph::FindAllPath(int** Array, Node startNodeKey, Node endNodeKey)
{
result[nPos] = startNodeKey.key; //将当前元素放入结果集中
Mark[startNodeKey.key - 1] = true; //将访问标记为已访问
nPos++; //结果集索引加1
while (nPos != 0)
{
int tempVal = result[nPos - 1]; //获取到最前面的元素
if (tempVal == endNodeKey.key) //若当前元素为目标节点
{
for (int j = 0; j < nPos; j++)
{
resultPath[pathNum][j] = result[j]; //将结果集复制于最后的路径矩阵中
}
nPos--; //回溯至上一个节点
result[nPos] = 0; //结果集对应索引置为空
pathNum++; //路径数目加1
Mark[endNodeKey.key - 1] = false;
break;
}
while (startNodeKey.flag < num) //利用flag来指示每次的元素的索引
{
if (Array[tempVal - 1][startNodeKey.flag] > 0 && Array[tempVal - 1][startNodeKey.flag] < maxValue)
{
if (Mark[startNodeKey.flag] == false) //利用Mark来判断是否已经访问过该节点
{
Node tempNode;
tempNode.key = startNodeKey.flag + 1;
FindAllPath(Array, tempNode, endNodeKey);//深度优先遍历算法,
}
}
startNodeKey.flag++; //索引值相应的加一
}
if (startNodeKey.flag == num) //如果已经是到最后的邻居,说明访问结束,
{ //将对应的值置为空
nPos--; //再次向上回溯
startNodeKey.flag = 0; //将节点的索引置为空
result[nPos] = 0; //将结果集中对应的索引置为空
Mark[startNodeKey.key - 1] = false; //访问之后标记为未访问。因为下面的元素已经访问结束,便于下次的访问 //
break;
}
}
};
//输出两点间的所有路径
void Graph::CoutAllPath(int v1, int v2)
{
int x, sum = 0;
Node headNode;//起始节点
Node endNode; //终止节点
stack<Node> tempStack;
for (int i = 0; i < num; i++)
{
for (int j = 0; j < num; j++)
{
resultPath[i][j] = 0;
}
result[i] = 0;
Mark[i] = false;
}
result[num] = 0;
pathNum = 0;
nPos = 0;
headNode.key = v1 + 1;
headNode.flag = 0; //起始节点
endNode.key = v2 + 1; //结束节点
FindAllPath(Edg(), headNode, endNode);
cout << "从" << getValue(v1).name << "到" << getValue(v2).name << "路径数目为:" << pathNum << endl;
for (int i = 0; i < pathNum; i++)
{
sum = 0;
cout << "第" << i + 1 << "条: ";
cout << getValue(headNode.key - 1).name;
v1 = headNode.key - 1;
for (int j = 1; j < num; j++)
{
if (resultPath[i][j] == 0)
{
break;
}
x = resultPath[i][j] - 1;
sum += getWeight(v1, x);
v1 = x;
cout << "-->" << getValue(x).name;
}
cout << endl << "路径长度为:" << sum << endl;
}
int i = 0;
};
//查找多个顶点间的最佳路径
int Graph::FindManyPath(int v, int x)
{
int j, k, n;
n = NumberOfVertices();
int* d = new int[n];
{
j = x;
k = 0;
while (j != v)
{
d[k++] = j;
j = path[j];
}
while (k > 0)
{
cout << "-->" << getValue(d[--k]).name;
}
}
delete[] d;
return dist[x]; //返回v到x的最短路径
};
//输出多个顶点间的最佳路径
void Graph::CoutMany()
{
system("cls");
Map();
int i, j, sum, x, a[num];
char c[num];
for (i = 0;; i++)
{
cout << "请输入你要参观的第" << i + 1 << "个景点(输入#结束): ";
cin >> c[i];
if (c[i] == '#')
break;
while (1)
{
a[i] = getVertexPos(c[i]);
if (a[i] == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "请输入你要参观的第" << i + 1 << "个景点(输入#结束): ";
cin >> c[i];
}
else
{
break;
}
}
}
cout << getValue(a[0]).name;
for (j = 0, sum = 0; j < i - 1; j++)
{
ShortestPath(a[j]);
x = FindManyPath(a[j], a[j + 1]);
sum += x;
}
cout << endl << "最短路径长度为:" << sum << endl;
cout << "按回车键继续";
getchar();
getchar();
};
//增加景点和道路
void Graph::Increase()
{
int f;
system("cls");
Map();
char code;
string name;
string intro;
cout << "请输入要增加的景点的代码:";
cin >> code;
while (1)
{
f = 0;
for (int i = 0; i < numVertices; i++)
{
if (code == getValue(i).code)
{
cout << "已有该代码请重新输入" << endl;
f = 1;
break;
}
}
if (f == 1)
{
cout << "请输入要增加的景点的代码:";
cin >> code;
}
else
{
break;
}
}
cout << "请输入要增加的景点的名称:";
cin.ignore();
getline(cin, name);
cout << "请输入要增加的景点的简介:";
getline(cin, intro);
insertVertex(code, name, intro);
int v1, v2, weight;
char code1, code2;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
cout << "请输入两景点间的距离:";
cin >> weight;
insertEdge(v1, v2, weight);
break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//景点信息查询
void Graph::search()
{
int i;
char code;
while (1)
{
system("cls");
Map();
cout << "请输入要查询的景点编号(输入#退出):";
cin >> code;
if (code == '#')
break;
i = getVertexPos(code);
if (i == -1)
{
cout << "输入错误,请重新输入" << endl;
}
else
{
Seek(i);
cout << "按回车键继续";
getchar();
getchar();
}
}
};
//查询两景点间最短距离
void Graph::shorest()
{
system("cls");
Map();
int v1, v2;
char code1, code2;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
ShortestPath(v1);
CoutShortest(v1, v2);
break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//查询任意两景点间的所有路径
void Graph::allpath()
{
system("cls");
Map();
int v1, v2;
char code1, code2;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
CoutAllPath(v1, v2); break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//动态生成景点列表
void Graph::Map()
{
cout << "***************************************" << endl;
cout << "***景点编号如下: ***" << endl;
for (int i = 1; i <= numVertices; i++)
{
cout << VerticesList[i - 1].code << std::left << setw(15) << VerticesList[i - 1].name;
if (i % 3 == 0)
cout << endl;
}
cout << endl << "***************************************" << endl;
};
5.4实验结果


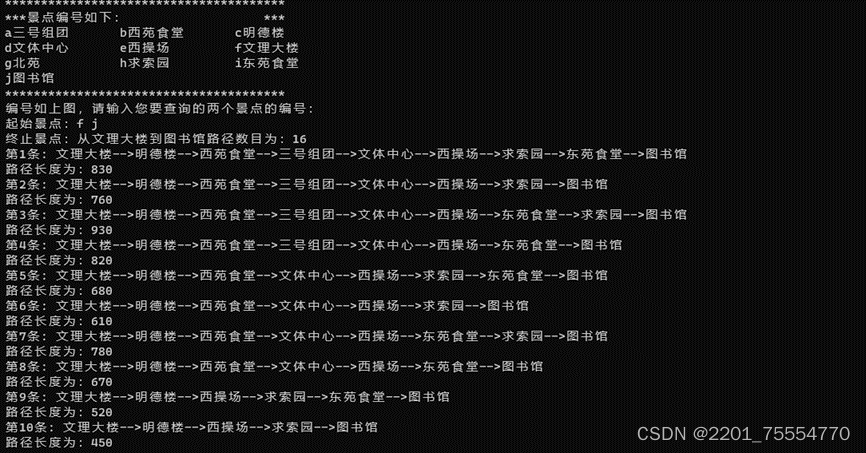
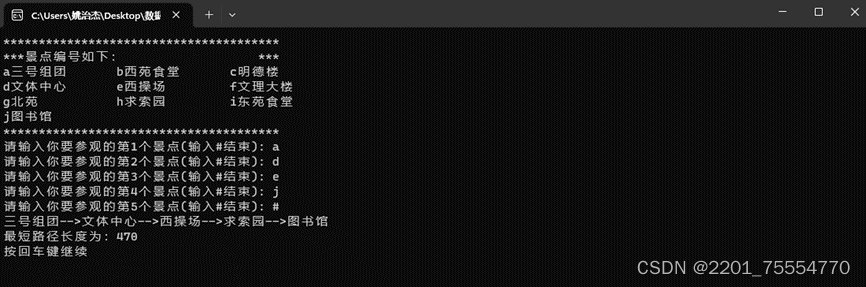
心得体会
“数据结构课程设计”是计算机科学与技术专业学生的集中实践性环节之一,是学习“数据结构”理论和实验课程后进行的一次全面的综合练习。其目的是要达到理论与实际应用相结合,提高学生组织数据及编写程序的能力,使学生能够根据问题要求和数据对象的特性,学会数据组织的方法,把现实世界中的实际问题在计算机内部表示出来并用软件解决问题,培养良好的程序设计技能。
我认为,在这学期的课程设计中,不仅培养了独立思考、动手操作的能力,在各种其它能力上也都有了提高。回顾起此课程设计,至今我仍感慨颇多,从理论到实践,在这段日子里,可以说得是苦多于甜,但是可以学到很多很多的东西,同时不仅可以巩固了以前所学过的知识,而且学到了很多在书本上所没有学到过的知识。
回顾此次实践过程,从一开始拿到题目时的无从下手,到后来的崎岖前行,直到最后成功的完成了三个小项目,其中饱含了艰辛,同时也提高了我的代码水平,培养了我的编程思想,磨练了我的耐心,让我能更全面、更细心地去分析和解决一个个实际问题。
虽然这次课程设计是在参考已有的数据结构的基础之上进行的,但是我觉得对自己是一个挑战和锻炼。我很欣慰自己能在程序中加入自己的想法和有关程序内容,也就是对它的程序改进了一番改进,并有创新。但是我感觉自己的创新还不够典型,总之还不是很满意。另外由于时间的紧迫和对知识的了解不够广泛,造成了系统中还存在许多不足,功能上还不够完善。以后我会继续努力,大胆创新,争取能编写出透射着自己思想的程序。这次课程设计让我充分认识到了自己的不足,认识到了动手能力的重要性。我会在以后的学习中更加努力锻炼自己,提高自己,让自己写出更好更完善的程序,为以后的编程打好基础!
这次课程中老师对我作品的讲评,让我明白在进行程序设计时,要注意想好思路,即要有恰当模块名、变量名、常量名、子程序名等。将每个功能的模块,即函数名要清晰的表述出来,使用户能够一目了然此程序的功能。当然适当的给写注释,也是方便用户的理解。还有在编写程序时要注意对程序的适当分配,便于用户看懂程序,也便于自己检查错误。但是完成任何一个较大的程序,都需要掌握一定的编程基础,需要不断的探索和求知过程,这样对自己编程能力的提高有较大的帮助。当然,任何程序必须经过计算机的调试,看是否调试成功,发现错误,一个个,一步步去解决,这样就能从错误中进步。
通过课程设计加强了我的动手能力,以及提升了局部和统一考虑问题的思维方式。回顾起此次课程设计,至今我仍感慨颇多。的确,从拿到题目到完成整个编程,从理论到实践,在整整一个星期的日子里,可以学到很多很多的的东西,同时不仅可以巩固了以前所学过的知识,而且学到了很多在书本上所没有学到过的知识。通过这次课程设计使我懂得了理论与实际相结合是很重要的,只有理论知识是远远不够的,只有把所学的理论知识与实践相结合起来,从理论中得出结论,才能真正为社会服务,从而提高自己的实际动手能力和独立思考的能力。在设计的.过程中遇到问题,可以说得是困难重重,这毕竟第一次做的,难免会遇到过各种各样的问题,同时在设计的过程中发现了自己的不足之处,对以前所学过的知识理解得不够深刻,掌握得不够牢固,通过这次课程设计之后,一定把以前所学过的知识重新温故。
完整代码
#include <iostream>
#include <fstream>
#include <string>
#include <vector>
#include <algorithm>
#include <iomanip>
#include <stack>
using namespace std;
// 定义参赛队基本信息结构体
struct Team {
string id; // 参赛队编号
string name; // 参赛作品名称
string school; // 参赛学校
string category; // 赛事类别
string members; // 参赛者
string instructor; // 指导老师
};
// 定义二叉排序树节点
struct BSTNode {
Team data; // 节点数据
BSTNode* left; // 左子树指针
BSTNode* right; // 右子树指针
};
// 二叉排序树类
class BST {
public:
// 插入节点
void insert(Team data);
// 删除节点
void remove(string id);
// 修改节点
void modify(string id, Team data);
// 查找节点
BSTNode* search(string id);
// 中序遍历
void inorderTraversal();
void inorderTraversal(BSTNode* node, vector<Team>& teams);
// 按学校或赛事类别查询参赛团队
void query(string keyword, bool searchBySchool);
// 计算子树高度
int height(BSTNode* node);
// 计算平均查找长度ASL
void ASL(BSTNode* node, int depth, int& sum);
BST() { root = NULL; }
~BST() { destroy(root); }
private:
// 销毁子树
void destroy(BSTNode* node);
// 根据关键字查询节点
vector<BSTNode*> queryNodes(string keyword, bool searchBySchool, BSTNode* node);
BSTNode* root;
};
// 插入节点
void BST::insert(Team data) {
BSTNode* node = new BSTNode();
node->data = data;
node->left = NULL;
node->right = NULL;
if (root == NULL) {
root = node;
}
else {
BSTNode* current = root;
while (true) {
if (data.id < current->data.id) {
if (current->left == NULL) {
current->left = node;
break;
}
else {
current = current->left;
}
}
else {
if (current->right == NULL) {
current->right = node;
break;
}
else {
current = current->right;
}
}
}
}
}
// 删除节点
void BST::remove(string id) {
BSTNode* parent = NULL;
BSTNode* current = root;
while (current != NULL && current->data.id != id) {
parent = current;
if (id < current->data.id) {
current = current->left;
}
else {
current = current->right;
}
}
if (current == NULL) {
return;
}
if (current->left == NULL) {
if (parent == NULL) {
root = current->right;
}
else {
if (current == parent->left) {
parent->left = current->right;
}
else {
parent->right = current->right;
}
}
delete current;
}
else if (current->right == NULL) {
if (parent == NULL) {
root = current->left;
}
else {
if (current == parent->left) {
parent->left = current->left;
}
else {
parent->right = current->left;
}
}
delete current;
}
else {
BSTNode* successorParent = current;
BSTNode* successor = current->right;
while (successor->left != NULL) {
successorParent = successor;
successor = successor->left;
}
if (successorParent != current) {
successorParent->left = successor->right;
successor->right = current->right;
}
if (parent == NULL) {
root = successor;
}
else {
if (current == parent->left) {
parent->left = successor;
}
else {
parent->right = successor;
}
}
successor->left = current->left;
delete current;
}
}
// 修改节点
void BST::modify(string id, Team data) {
remove(id);
insert(data);
}
// 查找节点
BSTNode* BST::search(string id) {
BSTNode* current = root;
while (current != NULL && current->data.id != id) {
if (id < current->data.id) {
current = current->left;
}
else {
current = current->right;
}
}
return current;
}
// 中序遍历
void BST::inorderTraversal() {
vector<Team> teams;
inorderTraversal(root, teams);
for (Team team : teams) {
cout << "参赛队编号:" << team.id << endl;
cout << "参赛作品名称:" << team.name << endl;
cout << "参赛学校:" << team.school << endl;
cout << "赛事类别:" << team.category << endl;
cout << "参赛者:" << team.members << endl;
cout << "指导老师:" << team.instructor << endl << endl;
}
}
void BST::inorderTraversal(BSTNode* node, vector<Team>& teams) {
if (node != NULL) {
inorderTraversal(node->left, teams);
teams.push_back(node->data);
inorderTraversal(node->right, teams);
}
}
// 按学校或赛事类别查询参赛团队
void BST::query(string keyword, bool searchBySchool) {
vector<BSTNode*> nodes = queryNodes(keyword, searchBySchool, root);
sort(nodes.begin(), nodes.end(), [](BSTNode* a, BSTNode* b) {
return a->data.category < b->data.category;
});
for (BSTNode* node : nodes) {
cout << "参赛队编号:" << node->data.id << endl;
cout << "参赛作品名称:" << node->data.name << endl;
cout << "参赛学校:" << node->data.school << endl;
cout << "赛事类别:" << node->data.category << endl;
cout << "参赛者:" << node->data.members << endl;
cout << "指导老师:" << node->data.instructor << endl << endl;
}
}
vector<BSTNode*> BST::queryNodes(string keyword, bool searchBySchool, BSTNode* node) {
vector<BSTNode*> nodes;
if (node != NULL) {
if ((searchBySchool && node->data.school == keyword) ||
(!searchBySchool && node->data.category == keyword)) {
nodes.push_back(node);
}
vector<BSTNode*> leftNodes = queryNodes(keyword, searchBySchool, node->left);
nodes.insert(nodes.end(), leftNodes.begin(), leftNodes.end());
vector<BSTNode*> rightNodes = queryNodes(keyword, searchBySchool, node->right);
nodes.insert(nodes.end(), rightNodes.begin(), rightNodes.end());
}
return nodes;
}
// 计算子树高度
int BST::height(BSTNode* node) {
if (node == NULL) {
return 0;
}
else {
int leftHeight = height(node->left);
int rightHeight = height(node->right);
return max(leftHeight, rightHeight) + 1;
}
}
// 计算平均查找长度ASL
void BST::ASL(BSTNode* node, int depth, int& sum) {
if (node != NULL) {
ASL(node->left, depth + 1, sum);
sum += depth;
ASL(node->right, depth + 1, sum);
}
}
// 销毁子树
void BST::destroy(BSTNode* node) {
if (node != NULL) {
destroy(node->left);
destroy(node->right);
delete node;
}
}
// 读取team.txt文件,生成二叉排序树
void readTeams(BST& bst) {
ifstream file("team.txt");
if (!file) {
cerr << "Error: team.txt does not exist" << endl;
return;
}
string line;
while (getline(file, line)) {
Team team;
team.id = line.substr(0, 5);
team.name = line.substr(6, 30);
team.school = line.substr(37, 20);
team.category = line.substr(58, 2);
team.members = line.substr(61, 100);
team.instructor = line.substr(162, 20);
bst.insert(team);
}
file.close();
}
const int maxValue = 9999;
const int maxVertices = 100; // 最大顶点数
const int DefaultVertices = 20; // 默认顶点数
const int num = 20;
struct ver //顶点的结构体
{
char code;
string name;
string intro;
};
struct Node //
{
int key;
int flag;
Node()
{
flag = 0;
}
};
class Graph //图的邻接矩阵类定义
{
public:
Graph(); // 构造函数
~Graph(); // 析构函数
int NumberOfVertices(); // 返回当前顶点数
int NumberOfEdges(); // 返回当前边数
ver getValue(int i); // 取顶点 i 的值
int getWeight(int v1, int v2); // 取边上权值
int getVertexPos(char code); // 给出顶点代码code在图中位置
bool insertVertex(char code, string name, string intro); // 插入一个顶点vertex
bool insertEdge(int v1, int v2, int cost); // 插入边(v1, v2), 权为cost
void Seek(int i); // 输出顶点i的信息
void ShortestPath(int v); // Dijkstra求最短路径算法
void CoutShortest(int v, int x); // 输出两顶点间的最短路径和距离
void FindAllPath(int** Array, Node startNodeKey, Node endNodeKey); // 查找两点间的所有路径
void CoutAllPath(int v1, int v2); // 输出两顶点间的所有路径
int FindManyPath(int v, int x); // 查找多个顶点间的最佳路径
void CoutMany(); // 输出多个顶点间的最佳路径
void Increase(); // 增加景点和道路
int** Edg() { return Edges; }; // 返回邻接矩阵
void search(); // 景点信息查询
void shorest(); // 查询两景点间最短距离
void allpath(); // 查询任意两景点间的所有路径
void Map(); // 动态生成景点列表
private:
int maxVertices; // 图中最大顶点数
int numEdges; // 当前边数
int numVertices; // 当前顶点数
ver* VerticesList; // 顶点表 (各边链表的头结点)
int** Edges; // 邻接矩阵保存边
int* path; // 保存该结点的前一个结点
int* dist; // 保存路径长度
int resultPath[num][num]; // 保存该结点的前一个结点
int result[num + 1]; // 保存结果集
bool Mark[num]; // 标记结点
int pathNum; // 两点间所有路径的数目
int nPos; // 栈中的顶点数
};
// 构造函数
Graph::Graph()
{
maxVertices = DefaultVertices; // 初始化 最大顶点数
numVertices = 0; // 初始化 顶点个数
numEdges = 0; // 初始化 边数
VerticesList = new ver[maxVertices]; // 创建顶点表数组
Edges = (int**) new int* [maxVertices]; // 创建邻接矩阵数组
for (int i = 0; i < maxVertices; i++)
Edges[i] = new int[maxVertices];
for (int i = 0; i < maxVertices; i++)
for (int j = 0; j < maxVertices; j++)
Edges[i][j] = (i == j) ? 0 : maxValue; // 邻接矩阵主对角线元素为0;顶点对间无边则权重无穷大
insertVertex('a', "三号组团", "三号组团为学生宿舍,由四栋并列的六层高楼组成。");
insertVertex('b', "西苑食堂", "位于学校西侧的学生食堂,分为三层,其中二楼为海洋船舶主题餐厅。");
insertVertex('c', "明德楼", "四栋教学楼之一。");
insertVertex('d', "文体中心", "学生进行体育课的地方,有乒乓球室、羽毛球室、飞镖房等。");
insertVertex('e', "西操场", "在文体中心对面,学生进行体育课的地方,旁边有网球场,轮滑场。");
insertVertex('f', "文理大楼", "江苏科技大学最高的楼,四栋教学楼之一,有着各种各样的教学设施。");
insertVertex('g', "北苑", "大部分学院的学院楼以及行政大楼所在地。");
insertVertex('h', "求索园", "绿荫小道,风景优美。");
insertVertex('i', "东苑食堂", "位于学校东侧的学生食堂。");
insertVertex('j', "图书馆", "拥有众多藏书以及学生自习的地方。");
insertEdge(0, 1, 100);
insertEdge(0, 3, 200);
insertEdge(1, 2, 80);
insertEdge(1, 3, 150);
insertEdge(2, 4, 120);
insertEdge(2, 5, 110);
insertEdge(3, 4, 50);
insertEdge(4, 7, 150);
insertEdge(4, 8, 230);
insertEdge(5, 6, 80);
insertEdge(5, 7, 60);
insertEdge(6, 9, 100);
insertEdge(7, 8, 90);
insertEdge(7, 9, 70);
insertEdge(8, 9, 50);
};
//析构函数
Graph::~Graph()
{
delete[] VerticesList;
delete[] Edges;
delete[] path;
delete[] dist;
};
//返回当前顶点数
int Graph::NumberOfVertices()
{
return numVertices;
};
//返回当前边数
int Graph::NumberOfEdges()
{
return numEdges;
};
// 取顶点 i 的值
ver Graph::getValue(int i)
{
return VerticesList[i];
};
// 取边上权值
int Graph::getWeight(int v1, int v2)
{
return Edges[v1][v2];
};
// 给出顶点代码code在图中位置
int Graph::getVertexPos(char code)
{
for (int i = 0; i < numVertices; i++)
if (VerticesList[i].code == code)
return i;
return -1;
};
// 插入一个顶点vertex
bool Graph::insertVertex(char code, string name, string intro)
{
if (numVertices == maxVertices)
return false;
VerticesList[numVertices].code = code;
VerticesList[numVertices].name = name;
VerticesList[numVertices].intro = intro;
numVertices++;
return true;
};
// 插入边(v1, v2), 权为cost
bool Graph::insertEdge(int v1, int v2, int weight)
{
if (v1 > -1 && v1<numVertices && v2>-1 && v2 < numVertices)
{
Edges[v1][v2] = Edges[v2][v1] = weight;
numEdges++;
return true;
}
else
return false;
};
// 输出顶点i的信息
void Graph::Seek(int i)
{
cout << "景点编号:" << VerticesList[i].code << endl;
cout << "景点名称:" << VerticesList[i].name << endl;
cout << "景点简介:" << VerticesList[i].intro << endl;
cout << "***************************************" << endl;
};
//查询两景点之间的最短路径和距离
void Graph::ShortestPath(int v)
{
int n = NumberOfVertices();
dist = new int[n];
path = new int[n];
bool* S = new bool[n]; //最短路径顶点集
int i, j, k, w, min;
for (i = 0; i < n; i++)
{
dist[i] = getWeight(v, i); //数组初始化
S[i] = false;
if (i != v && dist[i] < maxValue)
path[i] = v;
else
path[i] = -1;
}
S[v] = true; //顶点v加入顶点集合
dist[v] = 0;
for (i = 0; i < n - 1; i++)
{
min = maxValue;
int u = v; //选不在S中具有最短路径的顶点u
for (j = 0; j < n; j++)
if (S[j] == false && dist[j] < min)
{
u = j;
min = dist[j];
}
S[u] = true; //顶点u加入集合S
for (k = 0; k < n; k++) //修改
{
w = getWeight(u, k);
if (S[k] == false && w < maxValue && dist[u] + w < dist[k]) //顶点k未加入S,且绕过u可以缩短路径
{
dist[k] = dist[u] + w;
path[k] = u; //修改到k的最短路径
}
}
}
};
//输出两景点之间的最短路径和距离
void Graph::CoutShortest(int v, int x)
{
int j, k, n;
n = NumberOfVertices();
int* d = new int[n];
{
j = x;
k = 0;
while (j != v)
{
d[k++] = j;
j = path[j];
}
cout << getValue(v).name << "到" << getValue(x).name << "的最短路径为:" << endl << getValue(v).name;
while (k > 0)
{
cout << "-->" << getValue(d[--k]).name;
}
cout << endl << "最短路径长度为:" << dist[x] << endl;
}
delete[] d;
};
//查找两点间的所有路径
void Graph::FindAllPath(int** Array, Node startNodeKey, Node endNodeKey)
{
result[nPos] = startNodeKey.key; //将当前元素放入结果集中
Mark[startNodeKey.key - 1] = true; //将访问标记为已访问
nPos++; //结果集索引加1
while (nPos != 0)
{
int tempVal = result[nPos - 1]; //获取到最前面的元素
if (tempVal == endNodeKey.key) //若当前元素为目标节点
{
for (int j = 0; j < nPos; j++)
{
resultPath[pathNum][j] = result[j]; //将结果集复制于最后的路径矩阵中
}
nPos--; //回溯至上一个节点
result[nPos] = 0; //结果集对应索引置为空
pathNum++; //路径数目加1
Mark[endNodeKey.key - 1] = false;
break;
}
while (startNodeKey.flag < num) //利用flag来指示每次的元素的索引
{
if (Array[tempVal - 1][startNodeKey.flag] > 0 && Array[tempVal - 1][startNodeKey.flag] < maxValue)
{
if (Mark[startNodeKey.flag] == false) //利用Mark来判断是否已经访问过该节点
{
Node tempNode;
tempNode.key = startNodeKey.flag + 1;
FindAllPath(Array, tempNode, endNodeKey);//深度优先遍历算法,
}
}
startNodeKey.flag++; //索引值相应的加一
}
if (startNodeKey.flag == num) //如果已经是到最后的邻居,说明访问结束,
{ //将对应的值置为空
nPos--; //再次向上回溯
startNodeKey.flag = 0; //将节点的索引置为空
result[nPos] = 0; //将结果集中对应的索引置为空
Mark[startNodeKey.key - 1] = false; //访问之后标记为未访问。因为下面的元素已经访问结束,便于下次的访问 //
break;
}
}
};
//输出两点间的所有路径
void Graph::CoutAllPath(int v1, int v2)
{
int x, sum = 0;
Node headNode;//起始节点
Node endNode; //终止节点
stack<Node> tempStack;
for (int i = 0; i < num; i++)
{
for (int j = 0; j < num; j++)
{
resultPath[i][j] = 0;
}
result[i] = 0;
Mark[i] = false;
}
result[num] = 0;
pathNum = 0;
nPos = 0;
headNode.key = v1 + 1;
headNode.flag = 0; //起始节点
endNode.key = v2 + 1; //结束节点
FindAllPath(Edg(), headNode, endNode);
cout << "从" << getValue(v1).name << "到" << getValue(v2).name << "路径数目为:" << pathNum << endl;
for (int i = 0; i < pathNum; i++)
{
sum = 0;
cout << "第" << i + 1 << "条: ";
cout << getValue(headNode.key - 1).name;
v1 = headNode.key - 1;
for (int j = 1; j < num; j++)
{
if (resultPath[i][j] == 0)
{
break;
}
x = resultPath[i][j] - 1;
sum += getWeight(v1, x);
v1 = x;
cout << "-->" << getValue(x).name;
}
cout << endl << "路径长度为:" << sum << endl;
}
int i = 0;
};
//查找多个顶点间的最佳路径
int Graph::FindManyPath(int v, int x)
{
int j, k, n;
n = NumberOfVertices();
int* d = new int[n];
{
j = x;
k = 0;
while (j != v)
{
d[k++] = j;
j = path[j];
}
while (k > 0)
{
cout << "-->" << getValue(d[--k]).name;
}
}
delete[] d;
return dist[x]; //返回v到x的最短路径
};
//输出多个顶点间的最佳路径
void Graph::CoutMany()
{
system("cls");
Map();
int i, j, sum, x, a[num];
char c[num];
for (i = 0;; i++)
{
cout << "请输入你要参观的第" << i + 1 << "个景点(输入#结束): ";
cin >> c[i];
if (c[i] == '#')
break;
while (1)
{
a[i] = getVertexPos(c[i]);
if (a[i] == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "请输入你要参观的第" << i + 1 << "个景点(输入#结束): ";
cin >> c[i];
}
else
{
break;
}
}
}
cout << getValue(a[0]).name;
for (j = 0, sum = 0; j < i - 1; j++)
{
ShortestPath(a[j]);
x = FindManyPath(a[j], a[j + 1]);
sum += x;
}
cout << endl << "最短路径长度为:" << sum << endl;
cout << "按回车键继续";
getchar();
getchar();
};
//增加景点和道路
void Graph::Increase()
{
int f;
system("cls");
Map();
char code;
string name;
string intro;
cout << "请输入要增加的景点的代码:";
cin >> code;
while (1)
{
f = 0;
for (int i = 0; i < numVertices; i++)
{
if (code == getValue(i).code)
{
cout << "已有该代码请重新输入" << endl;
f = 1;
break;
}
}
if (f == 1)
{
cout << "请输入要增加的景点的代码:";
cin >> code;
}
else
{
break;
}
}
cout << "请输入要增加的景点的名称:";
cin.ignore();
getline(cin, name);
cout << "请输入要增加的景点的简介:";
getline(cin, intro);
insertVertex(code, name, intro);
int v1, v2, weight;
char code1, code2;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
cout << "请输入两景点间的距离:";
cin >> weight;
insertEdge(v1, v2, weight);
break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//景点信息查询
void Graph::search()
{
int i;
char code;
while (1)
{
system("cls");
Map();
cout << "请输入要查询的景点编号(输入#退出):";
cin >> code;
if (code == '#')
break;
i = getVertexPos(code);
if (i == -1)
{
cout << "输入错误,请重新输入" << endl;
}
else
{
Seek(i);
cout << "按回车键继续";
getchar();
getchar();
}
}
};
//查询两景点间最短距离
void Graph::shorest()
{
system("cls");
Map();
int v1, v2;
char code1, code2;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
ShortestPath(v1);
CoutShortest(v1, v2);
break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//查询任意两景点间的所有路径
void Graph::allpath()
{
system("cls");
Map();
int v1, v2;
char code1, code2;
cout << "编号如上图,请输入您要查询的两个景点的编号:" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
while (1)
{
v1 = getVertexPos(code1);
v2 = getVertexPos(code2);
if (v1 == -1 || v2 == -1)
{
cout << "输入错误,请重新输入" << endl;
cout << "起始景点:";
cin >> code1;
cout << "终止景点:";
cin >> code2;
}
else
{
CoutAllPath(v1, v2); break;
}
}
cout << "按回车键继续";
getchar();
getchar();
};
//动态生成景点列表
void Graph::Map()
{
cout << "***************************************" << endl;
cout << "***景点编号如下: ***" << endl;
for (int i = 1; i <= numVertices; i++)
{
cout << VerticesList[i - 1].code << std::left << setw(15) << VerticesList[i - 1].name;
if (i % 3 == 0)
cout << endl;
}
cout << endl << "***************************************" << endl;
};
//起始页
void start()
{
int i;
for (i = 0; i < 10; i++)
cout << endl;
cout << " *********************************************" << endl;
cout << " ** **" << endl;
cout << " ** 欢迎参观江苏科技大学导游图 **" << endl;
cout << " ** **" << endl;
cout << " *********************************************" << endl;
cout << "按回车键继续......";
getchar();
}
//菜单页
void meau()
{
cout << "*****************************************************************************************************************" << endl;
cout << "*** 欢迎使用校园导游咨询系统 ***" << endl;
cout << "*** 输入1 增加参赛队伍信息 ***" << endl;
cout << "*** 输入2 删除参赛队伍信息 ***" << endl;
cout << "*** 输入3 修改参赛队伍信息 ***" << endl;
cout << "*** 输入4 查找参赛队伍信息 ***" << endl;
cout << "*** 输入5 中序遍历参赛队伍信息 ***" << endl;
cout << "*** 输入6 按学校查询参赛团队 ***" << endl;
cout << "*** 输入7 按赛事类别查询参赛团队 ***" << endl;
cout << "*** 输入8执行景点信息查询 ***" << endl;
cout << "*** 输入9执行查询两景点间最短距离 ***" << endl;
cout << "*** 输入10执行查询任意两景点间的所有路径 ***" << endl;
cout << "*** 输入11执行查询多个景点间的最佳路径 ***" << endl;
cout << "*** 输入12执行增加景点和道路 ***" << endl;
cout << "*** 输入0执行退出系统 ***" << endl;
cout << "*****************************************************************************************************************" << endl;
}
// 主函数
int main() {
BST bst;
// 读取team.txt文件,生成二叉排序树
readTeams(bst);
Graph g;
string c;
int choice;
while (true) {
system("cls");
meau();
cout << "请输入您要执行功能的编号:";
cin >> choice;
/*if (c.length() == 1)
choice = (c.at(0) - 48);
else
choice = 100;
if (choice < 0 || choice>5)
{
cout << "输入错误,请重新输入!" << endl;
}
cin.ignore();
*/
switch (choice) {
case 1: {
system("cls");
Team team;
cout << "输入参赛队编号:";
getline(cin, team.id);
cout << "输入参赛作品名称:";
getline(cin, team.name);
cout << "输入参赛学校:";
getline(cin, team.school);
cout << "输入赛事类别:";
getline(cin, team.category);
cout << "输入参赛者信息:";
getline(cin, team.members);
cout << "输入指导老师信息:";
getline(cin, team.instructor);
bst.insert(team);
cout << "成功插入参赛队伍信息" << endl;
break;
}
case 2: {
system("cls");
string id;
cout << "输入要删除的参赛队编号:";
getline(cin, id);
BSTNode* node = bst.search(id);
if (node != NULL) {
bst.remove(id);
cout << "成功删除参赛队伍信息" << endl;
}
else {
cout << "未找到该参赛队伍信息" << endl;
}
break;
}
case 3: {
system("cls");
string id;
cout << "输入要修改的参赛队编号:";
getline(cin, id);
BSTNode* node = bst.search(id);
if (node != NULL) {
Team team;
cout << "输入新的参赛作品名称:";
getline(cin, team.name);
cout << "输入新的参赛学校:";
getline(cin, team.school);
cout << "输入新的赛事类别:";
getline(cin, team.category);
cout << "输入新的参赛者信息:";
getline(cin, team.members);
cout << "输入新的指导老师信息:";
getline(cin, team.instructor);
bst.modify(id, team);
cout << "成功修改参赛队伍信息" << endl;
}
else {
cout << "未找到该参赛队伍信息" << endl;
}
break;
}
case 4: {
system("cls");
string id;
cout << "输入要查找的参赛队编号:";
getline(cin, id);
BSTNode* node = bst.search(id);
if (node != NULL) {
cout << "参赛作品名称:" << node->data.name << endl;
cout << "参赛学校:" << node->data.school << endl;
cout << "赛事类别:" << node->data.category << endl;
cout << "参赛者:" << node->data.members << endl;
cout << "指导老师:" << node->data.instructor << endl;
int sum = 0;
//BST::ASL(bst.search(id), 0, sum);
//cout << "平均查找长度ASL:" << sum << "/" << BST::height(bst.search(id)) << "=" << sum * 1.0 / BST::height(bst.search(id)) << endl;
}
else {
cout << "查找失败!" << endl;
}
break;
}
case 5: {
system("cls");
cout << "所有参赛队伍信息如下:" << endl << endl;
bst.inorderTraversal();
break;
}
case 6: {
system("cls");
string school;
cout << "输入要查询的参赛学校:";
getline(cin, school);
cout << "查询结果如下:" << endl << endl;
bst.query(school, true);
break;
}
case 7: {
system("cls");
string category;
cout << "输入要查询的赛事类别:";
getline(cin, category);
cout << "查询结果如下:" << endl << endl;
bst.query(category, false);
break;
}
case 8: //景点信息查询
g.search();
break;
case 9: //查询两景点间最短距离
g.shorest();
break;
case 10: //查询任意两景点间的所有路径
g.allpath();
break;
case 11: //查询多个景点间的最佳路径
g.CoutMany();
break;
case 12: //增加景点和道路
g.Increase();
break;
case 13:
start();
break;
case 0: //结束程序
cout << "谢谢您的使用!" << endl;
return 0;
default: {
cout << "请输入正确的数字!" << endl;
break;
}
}
}
return 0; // 返回退出
}




















 4377
4377










