【ICPC-243】hdu 3306 Another kind of Fibonacci-优快云博客

本文链接：https://blog.youkuaiyun.com/chenguolinblog/article/details/10439691

本文介绍了一种利用矩阵快速幂解决特定递推序列平方和问题的方法。针对递推公式A(N)=X*A(N-1)+Y*A(N-2)，通过构造特定矩阵，实现了高效求解A(0)^2+A(1)^2+…+A(n)^2的方案，并提供了完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

点击打开hdu 3306

思路: 矩阵快速幂

分析:

1 题目给定另外一种递推式，A(0) = 1 , A(1) = 1 , A(N) = X * A(N - 1) + Y * A(N - 2) (N >= 2).求 S(N) , S(N) = A(0)2 +A(1)2+……+A(n)2

2 那么我们通过这个式子就可以构造出以下的矩阵

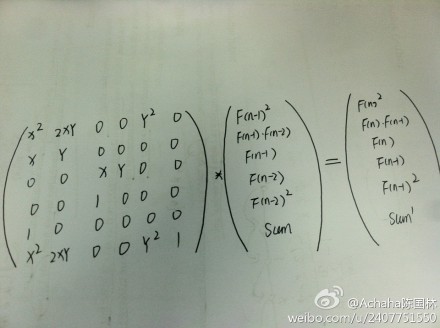
代码:

/************************************************
 * By: chenguolin                               * 
 * Date: 2013-08-28                             *
 * Address: http://blog.youkuaiyun.com/chenguolinblog *
 ************************************************/
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

const int MOD = 10007;
const int N = 6;

int n , x , y;
struct Matrix{
    int mat[N][N];
    Matrix operator*(const Matrix& m)const{
         Matrix tmp;
         for(int i = 0 ; i < N ; i++){
             for(int j = 0 ; j < N ; j++){
                 tmp.mat[i][j] = 0;
                 for(int k = 0 ; k < N ; k++)
                     tmp.mat[i][j] += mat[i][k]*m.mat[k][j]%MOD;
                 tmp.mat[i][j] %= MOD;  
             }
         }
         return tmp;
    }
};

void init(Matrix &m){
    memset(m.mat , 0 , sizeof(m.mat));
    x %= MOD , y %= MOD;
    m.mat[0][0] = m.mat[5][0] = x*x%MOD;
    m.mat[0][1] = m.mat[5][1] = 2*x*y%MOD;
    m.mat[0][4] = m.mat[5][4] = y*y%MOD;
    m.mat[1][0] = x ; m.mat[1][1] = y;
    m.mat[2][2] = x ; m.mat[2][3] = y;
    m.mat[3][2] = m.mat[4][0] = 1;
    m.mat[5][5] = 1;
}

int Pow(Matrix m){
    Matrix ans;
    memset(ans.mat , 0 , sizeof(ans.mat));
    for(int i = 0 ; i < N ; i++)
        ans.mat[i][i] = 1;
    n--;
    while(n){
        if(n%2)
            ans = ans*m;
        n /= 2;
        m = m*m;
    }
    int sum = 0;
    sum += ans.mat[5][0]%MOD;
    sum += ans.mat[5][1]%MOD;
    sum += ans.mat[5][2]%MOD;
    sum += ans.mat[5][3]%MOD;
    sum += ans.mat[5][4]%MOD;
    sum += ans.mat[5][5]*2%MOD;
    return sum%MOD;
}

int main(){
    Matrix m;
    while(scanf("%d%d%d" , &n , &x , &y) != EOF){
         init(m);
         printf("%d\n" , Pow(m));
    }
    return 0;
}