基于OpenCL的图像积分图算法实现

积分图的概念

图像积分图算法在图像特征检测中有着比较广泛的应用，主要用于规则区域特征值的计算。
积分图的概念可用下图表示：

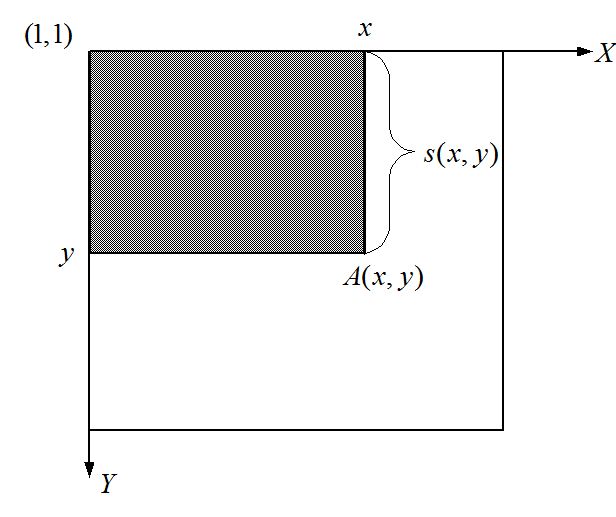
坐标A(x,y)的积分图是其左上角的所有像素之和（图中的阴影部分）。定义为：

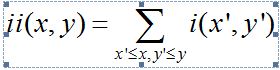
在上图中，A(x,y)表示点(x,y)的积分图；s(x,y)表示点(x,y)的y方向的所有原始图像之和。

积分图算法在CPU上的串行实现

在CPU上串行实现积分图计算的典型代码如下：

	/*
	 * 标准的积分图算法(cpu)
	 * 返回积分图矩阵对象
	 * is_square为true时为积方图对象
	 */
	template<typename _E=E
		,typename _ENABLE=typename std::enable_if<sizeof(_E)<=sizeof(cl_ulong)>::type>
	integral_matrix integral_cpu(bool is_square)const {
		throw_if(this->get_row_stride()*this->height!=this->v.size())
		auto integ_mat = integral_matrix(this->width,this->height);
		// 行宽度
		const auto row_stride = this->get_row_stride();
		if (!integ_mat.v.size())
			integ_mat.v = std::vector<integral_matrix::element_type>(row_stride * this->height);
		auto last_line	= integ_mat.v.data(); // 积分图上一行指针
		auto cur_line 	= last_line;			// 积分图当前行指针
		auto src_line 	= this->v.data();		// 原图当前行指针
		// 计算第一行前缀和
		prefix_sum(src_line, cur_line, this->width,is_square);
		src_line += row_stride;	// 积分图当前行指针步进一行
		cur_line += row_stride;
		integral_matrix::element_type line_sum; // 积分图当前行所有元素之和
		typename std::decay<decltype(this->height)>::type y;
		typename std::decay<decltype(this->width )>::type x;
		// 从第二行开始计算积分图
		if(is_square){
			for (y = 1; y < this->height;	++y,
													src_line	+= row_stride,
													cur_line	+= row_stride,
													last_line+= row_stride) {
				line_sum = 0;
				for ( x = 0; x < this->width; ++x) {
					line_sum += src_line[x]*src_line[x];
					cur_line[x] = line_sum + last_line[x];
				}
			}
		}else{
			for (y = 1; y < this->height;	++y,
													src_line	+= row_stride,
													cur_line	+= row_stride,
													last_line+= row_stride) {
				line_sum = 0;
				for ( x = 0; x < this->width; ++x) {
					line_sum += src_line[x];
					cur_line[x] = line_sum + last_line[x];
				}
			}
		}
		return std::move(integ_mat);//返回积分图对象
	}

前缀和(prefix sum)

说到积分图，就得引入前缀和(prefix sum)的概念:
给定一个数组A[1…n]，前缀和数组prefix_sum[1…n]定义为：prefix_sum[i] = A[0]+A[1]+…+A[i-1]；
例如：A[5,6,7,8] --> prefix_sum[5,11,18,26]
prefix_sum[0] =A[0] ;
prefix_sum[1] =A[0] + A[1] ;
prefix_sum[2] =A[0] + A[1] + A[2] ;
prefix_sum[3] =A[0] + A[1] + A[2] + A[3] ;

下面是前缀和数组计算的典型代码，非常简单

/* 前缀和计算模板函数 is_square为true时计算平方和*/
template<typename _T1,typename _T2,
	typename _ENABLE=typename std::enable_if<sizeof(_T1)<=sizeof(_T2)>::type>
inline static void prefix_sum(const _T1 *const src,_T2 *const dst,size_t size,bool is_square){
	assert(nullptr!=src&&nullptr!=dst);
	if(is_square){
		dst[0] = src[0]*src[0];
		for( size_t i=1; i<size; ++i)	dst[i]=(_T2)(src[i])*(_T2)(src[i])+dst[i-1];
	}
	else{
		dst[0] = src[0];
		for( size_t i=1; i<size; ++i)	dst[i]=(_T2)(src[i])+dst[i-1];
	}
}

OpenCL并行实现

积分图也可以用下面的公式（2）和公式（3）得出：

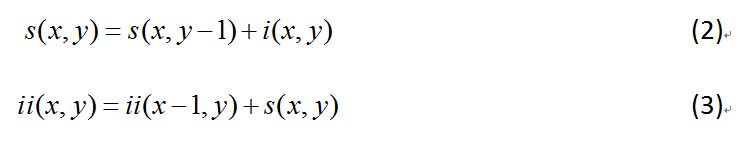
从公式（2）和公式（3）可以看出，积分图的算法类似于前缀和计算(prefix sum)

对于只有一行的像素的图像，它的积分图就是其前缀和数组

所以,如果要用OpenCL并行计算图像矩阵A的积分图，可以把积分图算法分拆成两个步骤：

1. 首先计算矩阵A在x方向的前缀和矩阵A1
2. 然后再在计算矩阵A1在y方向前缀和矩阵A2,A2就是图像矩阵A的积分图矩阵。

在OpenCL实现中为了提高内存访问性能，计算矩阵A1在y方向前缀和矩阵的时候，通常先将矩阵A1转置，然后再进行计算x方向的前缀和。

所以OpenCL具体实现的时候，分为下面4步

1. 计算矩阵A在x方向的前缀和矩阵A1
2. A1转置
3. 计算矩阵A1在x方向的前缀和矩阵A2
4. A2转置
   也就是说，基于OpenCL的积分图算法最终被分解为两次x方向前缀和计算和2次矩阵转置

下面是主机端的部分实现代码：

/*
 * 计算图像的积分图/积方图，
 * 返回积分图矩阵对象
 * is_square为true时为积方图对象
 */
gray_matrix_cl::integral_matrix gray_matrix_cl::integral(bool is_square) const {
	auto integral_mat1=to_matrix_cl().prefix_sum_line<cl_uint>(std::string(KERNEL_NAME(prefix_sum_line)"_uchar_uint"),is_square);//执行kernel,计算x方向前缀和
	//原图为灰度图像矩阵，所以原图元素类型为uchar,生成的前缀和矩阵integral_mat1的元素类型为uint
	integral_mat1= integral_mat1.transpose(KERNEL_NAME(matrix_transpose)"_uint");//执行kernel,integral_mat1矩阵转置
	auto integral_mat2=integral_mat1.prefix_sum_line<cl_ulong>(std::string(KERNEL_NAME(prefix_sum_line)"_uint_ulong"),false);//执行kernel,计算x方向前缀和
	// 源矩阵integral_mat1的元素类型为uint,生成的前缀和矩阵元素类型为ulong
	integral_mat2= integral_mat2.transpose(KERNEL_NAME(matrix_transpose)"_ulong");//执行kernel,integral_mat2矩阵转置
	return std::move(integral_mat2);//返回积分图对象
}

/*
 * 计算矩阵中的每一行的前缀和(prefix_sum)
 * 结果输出到int_mat
 */
template< typename DST_E,
		typename _CL_TYPE=CL_TYPE,typename _E=E,
		typename _ENABLE=typename 	std::enable_if<std::is_scalar<_E>::value
												&&std::is_scalar<DST_E>::value
												&&sizeof(DST_E)>=sizeof(_E)
			  	  	  	  	  	  	  	  	  	&&std::is_base_of<cl::Buffer,_CL_TYPE>::value
												>::type>
matrix_cl<DST_E,cl::Buffer>
prefix_sum_line(const std::string &kernel_name,bool is_square)const{
	this->check_cl_mem_obj(SOURCE_AT);
	auto context=dynamic_cast<const cl::Memory&>(this->cl_mem_obj).getInfo<CL_MEM_CONTEXT>();
	matrix_cl<DST_E,cl::Buffer> integral_mat(width, height,0,context);
	cl::CommandQueue q = cl::CommandQueue(context);
	run_kernel(global_facecl_context.getKernel(kernel_name)
		, cl::EnqueueArgs(q, { 1, height })//每个work-iteam处理1行
		, false
		, *this
		, integral_mat
		, width
		, get_row_stride()
		, is_square?CL_TRUE:CL_FALSE
		);
	return std::move(integral_mat);
}
/*
 * 矩阵转置
 */
template<typename _CL_TYPE=CL_TYPE>
typename std::enable_if<std::is_base_of<cl::Buffer, _CL_TYPE>::value,self_type>::type
transpose(const std::string &kernel_name)const{
	this->check_cl_mem_obj(SOURCE_AT);
	auto context = dynamic_cast<const cl::Memory&>(this->cl_mem_obj).getInfo<CL_MEM_CONTEXT>();
	self_type dst_mat(height, width, align_v, context);
	dst_mat.align_v = this->align; // 记录转置前的水平对齐值 
	cl::CommandQueue queue = cl::CommandQueue(context);
	run_kernel(global_facecl_context.getKernel(kernel_name)
			, cl::EnqueueArgs(queue,{ 1, height })//每个work-iteam处理1行
			, false
			, *this
			, dst_mat
			, width
			, this->get_row_stride()
			, dst_mat.get_row_stride()
		);
	return std::move(dst_mat);
}

上面代码中用到的run_kernel函数参见我的博客[《opencl🆑:make_kernel的进化》][2]

下面是上面代码中执行的kernel函数prefix_sum_line的代码，每个work-item处理一行数据，实现的功能很简单，就是计算矩阵中一行数据的前缀和(prefix sum),
为减少对global内存的访问，kernel函数中用到了local memory(代码中的local_block数组)来暂存每行的部分数据。local_block数组的大小在编译内kernel代码时由编译器提供,参见我的博客[《opencl::kernel中获取local memory size》][1]

 ///////////////////////////////////////////////////////////////////////////////
//! @file	: prefix_sum_line.cl
//! @date   : 2016/03/04
//! @author: guyadong
//! @brief  : Calculates the integral sum scan of an image
////////////////////////////////////////////////////////////////////////////////

 #ifndef CL_DEVICE_LOCAL_MEM_SIZE //local memory的大小，由编译器提供
 #error not defined CL_DEVICE_LOCAL_MEM_SIZE by complier with options -D
 #endif
 #ifndef SRC_TYPE //源矩阵数据类型 uchar,uinit,ulong.....
 #error not defined SRC_TYPE by complier with options -D
 #endif
 #ifndef DST_TYPE //目标矩阵数据类型 uchar,uinit,ulong.....
 #error not defined DST_TYPE by complier with options -D
 #endif
 
 #define LOCAL_BUFFER_SIZE (CL_DEVICE_LOCAL_MEM_SIZE/sizeof(DST_TYPE))//编译时确定local buffer数组的大小
  
#define _KERNEL_NAME(s,d) prefix_sum_line_##s##_##d
#define KERNEL_NAME(s,d) _KERNEL_NAME(s,d)
// kernel function的名字在编译期根据SRC_TYPE 和DST_TYPE添加类型后缀

///////////////////////////////////////////////////////////////////////////////
//! @brief  :	Calculates the prefix sum for each line of an image if is_square is CL_FALSE,
// 					Calculates the prefix sum of is_square if is_square is CL_TRUE, 
////////////////////////////////////////////////////////////////////////////////
 __kernel void KERNEL_NAME(SRC_TYPE,DST_TYPE)( __global SRC_TYPE *sourceImage, __global DST_TYPE * dest, int width, int width_step,int is_square ){
 	__local DST_TYPE local_block[ LOCAL_BUFFER_SIZE ];
  	const int line_index = get_global_id(1)*width_step;// 计算当前行的起始位置
 	__global SRC_TYPE * const src_ptr	= line_index + sourceImage;// 源矩阵的起始指针
 	__global DST_TYPE * const dst_ptr	= line_index + dest; 	// 目标矩阵的起始指针
 	__global SRC_TYPE * block_src_ptr	= src_ptr;	
 	__global DST_TYPE * block_dst_ptr	= dst_ptr; 	
 	int block_size = 0; // 块大小
 	DST_TYPE last_sum=0;// 上一块数组的前缀和
 	// 将一行数据按local_block数组的大小来分块处理
	for( int start_x = 0 ; start_x < width ; 
			start_x 				+= LOCAL_BUFFER_SIZE,
			block_src_ptr		+= LOCAL_BUFFER_SIZE,
			block_dst_ptr 	+= LOCAL_BUFFER_SIZE,
			last_sum 			+= local_block[block_size -1] ){
		block_size = min( (int)LOCAL_BUFFER_SIZE, width - start_x );
		// compute prefix sum of a block with local memory		
		if(is_square){
			local_block[0] = last_sum + ((DST_TYPE)block_src_ptr[0])*((DST_TYPE)block_src_ptr[0]);
			for( int i=1; i<block_size; ++i)	local_block[i]=((DST_TYPE)block_src_ptr[i])*((DST_TYPE)block_src_ptr[i])+local_block[i-1];
		}else{
			local_block[0] = last_sum + (DST_TYPE)block_src_ptr[0];
			for( int i=1; i<block_size; ++i)	local_block[i]=block_src_ptr[i]+local_block[i-1];
		} 		
		// copy local_block to dest
		for(int i = 0 ; i < block_size; ++i){
			block_dst_ptr[i]=local_block[i];
		}		
	}
 }
 

矩阵转置的kernel代码，每个work-item处理一行数据

 ///////////////////////////////////////////////////////////////////////////////
//! @file	: matrix_transpose.cl
//! @date   : 2016/03/04
//! @author: guyadong
//! @brief  : matrix transpose
////////////////////////////////////////////////////////////////////////////////
 #ifndef SRC_TYPE 
 #error not defined SRC_TYPE by complier with options -D
 #endif
#define _KERNEL_NAME(s) matrix_transpose_##s
#define KERNEL_NAME(s) _KERNEL_NAME(s) 
// kernel function的名字在编译期根据SRC_TYPE 加一个类型后缀
 
 __kernel void KERNEL_NAME(SRC_TYPE)( __global SRC_TYPE *matrix_src,__global SRC_TYPE *matrix_dst, int width, int src_width_step,int dst_width_step ){
   	const int y 				= get_global_id(1);
   	__global SRC_TYPE * src_ptr	= matrix_src + y*src_width_step;
	for( int x = 0; x < width; ++x,++src_ptr ){
		matrix_dst[  x*dst_width_step + y ] = *src_ptr;
	} 
 }

补充：
后来我对这个算法进行了改进，参见我的后续博文《基于OpenCL的图像积分图算法改进》

参考文章

[《AdaBoost人脸检测算法1（转）》][3]
[《基于OpenCL的图像积分图算法优化研究》][4]
[1]:http://blog.youkuaiyun.com/10km/article/details/50802638
[2]:http://blog.youkuaiyun.com/10km/article/details/50832741
[3]:http://blog.sina.com.cn/s/blog_7769660f01019ep0.html
[4]:http://www.doc88.com/p-9933630209054.html