邻接矩阵特征
Floyd算法建立在对图的邻接矩阵的操作上,理解Floyd首先要理解邻接矩阵
对于有向图,邻接矩阵的一行代表该顶点的出边,一列代表该顶点的入边
对于无向图则不区分出边与入边,邻接矩阵表示成一个对称矩阵

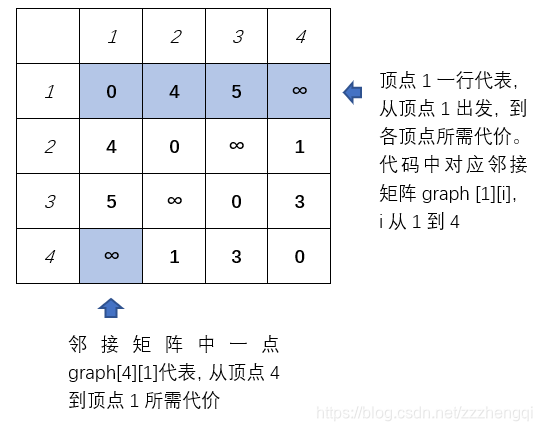
graph[i][j] 代表 i -> j ,由 i 直接到 j 的代价,graph[i][k] + graph[k][j]就表示 (i -> k) + (k -> j) ,即 i -> k -> j ,由 i 经 k 到 j 的代价
Floyd代码中有三层for循环,其中最内层for就是在操作这样一个值 + 一行值
下面以上图为例,分析Floyd算法运行过程
Floyd算法
Floyd算法中使用一个三维数组 ans[k][i][j],表示可以经过的中间结点序号小于等于 k 时,顶点 i 到顶点 j 的最小代价
① ans[0][i][j]的值即邻接矩阵
② ans[1][i][j]的值即,可以经过顶点 1 ,各顶点对间最小代价,这个值是在ans[0][i][j]的基础上得到的。
经过顶点 1 有什么好处?
以前只有 i -> j 的边能用,现在 i -> 1 -> j 的边也能用了,表现在邻接矩阵上就是,以前的代价是graph[i][j],现在可以是
graph[i][1] + graph[1][j]了,即在这个三维矩阵中ans[1][i][j]的值应该等于min{ans[0][i][j], ans[0][i][1] + ans[0][1][j]},经过这样的比较,就将顶点 1 能产生的影响考虑了进去。
③ 同上,将所有顶点都考虑进去,就得到了整个图中顶点对的最短路径
代码实现与分析
代码中实际使用的是一个二维数组ans[i][j],下面先给出代码,然后在解释代码中分析使用二维而不是三维的可行性
#include <iostream>
using namespace std;
#define MAXN 110
int ans[MAXN][MAXN];
int main() {
int n, m; //n个顶点,序号为 1 到 n, m条边
while (cin >> n >> m) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
ans[i][j] = -1; //不可达
}
ans[i][i] = 0;
}
for (int i = 0; i < m; i++) { //顶点u到顶点v,代价为w
int u, v, w;
cin >> u >> v >> w; //顶点从1开始编号
ans[u][v] = w;
ans[v][u] = w;
}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (ans[i][k] == -1 || ans[k][j] == -1)
continue;
if (ans[i][j] == -1 || ans[i][j] < ans[i][k] + ans[k][j])
ans[i][j] = ans[i][k] + ans[k][j];
}
}
}
}
}代码的核心就是三层for循环,三个for各有各的作用。首先要明确的是,三层for的最终目的就是要求出ans[n][i][j],ans[n][i][j]是将所有顶点能产生的影响都考虑进去时,各顶点对的最短路径。
①最内层for,k不变,i不变,j遍历所有顶点

比如k = 1,i = 3,j = 1...4,实现的是修改ans[3][j],顶点 3 到各顶点最小代价,即第三行值,考虑的是顶点k = 1的影响,顶点k = 1能对顶点 3 产生的影响就是,从顶点 3 走向顶点 1 ,再从顶点1去各顶点,这个代价与原来不考虑1的哪个小,就是
ans[3][j] = min(ans[3][1] + ans[1][j], ans[3][j]),从图上来看,3->1,应该找3行1列,再1->*,应该找1行*列,将这两步代价相加即3->*代价,图上是深蓝方块去加浅蓝方块,再与对应黄色方块比较,并修改黄色方块
最内层for修改的是,考虑需要小于k的顶点时,矩阵第i行的值,是顶点 i 考虑顶点k后的结果
②中间层for,j 遍历各个顶点,每个顶点都考虑一次顶点k产生的影响,就是顶点k对整个图产生的影响
③最外层for,k 遍历各个顶点,整个矩阵对每个顶点的影响都考虑一次,就是所有顶点对整个图产生的影响,即最终所求
二维替代三维
现在再来说明为什么能用二维数组替代三维数组

最外层for每轮要将这个二维数组所有元素修改一遍,从代码中可以看出,用来比较的,即需要其值不被随意改动的是一行一列的元素,修改其他9个白色方块时自然不会对这7个蓝色方块造成影响,而修改蓝色方块时呢?
①深蓝:即j = k,ans[i][k] = min(ans[i][k] + ans[k][k], ans[i][k]) ,ans[k][k]是自己到自己一定为0
②浅蓝:即i = k,ans[k][j] = min(ans[k][k] + ans[k][j], ans[k][j]),ans[k][k]同样为0
可以看出两种情况都不会造成影响,蓝色方块在这一轮k中是固定不变的,从算法上理解就是要考虑的中间顶点是k,如果k是两端结点,那么某个顶点经过k再到k,这个值就是这个顶点直接到k的值,另一端同理,从k经k到某个顶点=从k到某个顶点
既然没影响,自然可以在原地修改数组中的元素值
这里需要特别注意的是,最外层for每轮计算一个顶点能产生的影响,这个影响是该顶点在当前状态下能产生的直接影响,也就是顶点1能产生的影响,并不是在计算过k=1之后就固定了,只是在算法运行过程中,先把顶点1的影响加入,在后续过程中持续发挥着作用
比如,
k = 0时只将graph[i][j]考虑进去,
k = 1时将graph[i][j],graph[i][1] + graph[1][j]考虑进去
k = 2时将graph[i][j],graph[i][1] + graph[1][j],graph[i][1] + graph[1][2] + graph[2][j],graph[i][2] + graph[2][j]考虑进去,此时顶点1的影响不仅局限于k = 1那一轮计算过的graph[i][1] + graph[1][j],还有graph[i][1] + graph[1][2] + graph[2][j],先经1再经2
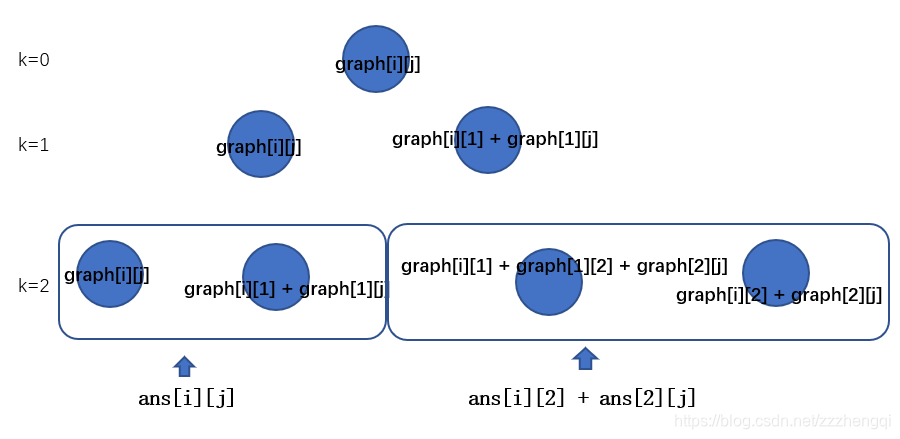
k = 2时看似是比较了两个值,其实是将四种路径进行比较取最小值,这样到最后一轮,就是所有路径的最小值






















 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








