Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

最新推荐文章于 2025-12-09 15:45:55 发布

原创

最新推荐文章于 2025-12-09 15:45:55 发布 · 1k 阅读

27 ·

CC 4.0 BY-SA版权

文章标签：

#kotlin #开发语言 #android

论文链接：Visual Autoregressive Modeling: Scalable Image Generation via Next-Scale Prediction

文章目录

简介
预测下一个token自回归模型范式分析
VAR详解
结论

简介

本文提出的视觉自回归建模/VAR这种新范式，其将图像的自回归学习重新定义为从粗到细的“下一个尺度预测”或“下一个分辨率预测”，与常规的LLM预测下一个token的范式不同。VAR首次基于GPT架构的AR模型在图片生成方面超过了扩散模型，在 ImageNet 256×256 基准测试中，FID、IS分数均大幅提高，推理速度也快了将近20倍。实验证实，VAR在图像质量、推理速度、数据效率和可扩展性等多个维度由于DiT，且其具有明显的Scaling规律，在图像修复、外绘、编辑等下游任务中具有较好的泛化能力。
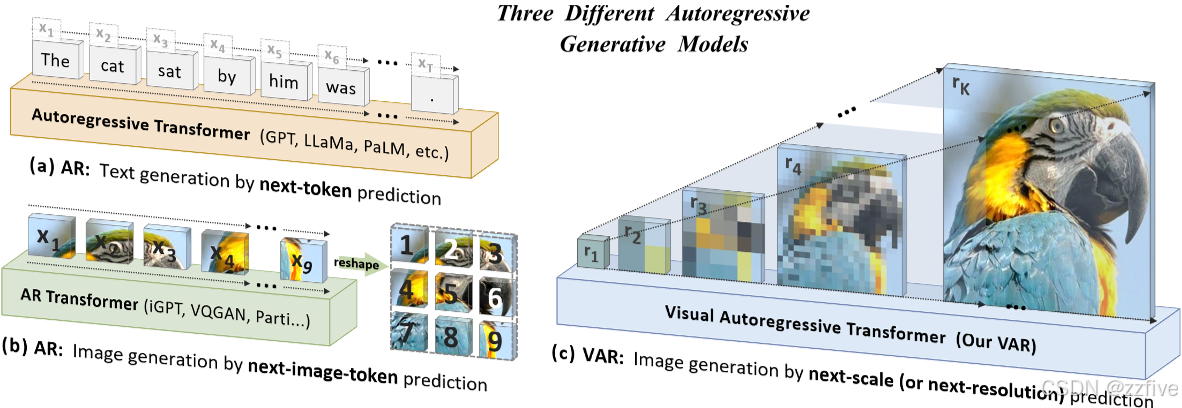
在这里插入图片描述

图1 不同自回归生成模型

图1中对比展示了三种自回归生成模型，(a)中是常规的基于预测下一个token范式的自回归模型/AR，GPT、LLaMa等LLM模型均是此范式；(b)中是与(a)一样，以光栅扫描将连续图片转换为离散tokens，通过预测下一个token进行图片生成的自回归模型；©中是文本提出的VAR，即从粗到细的多尺度自回归预测模型，可以看出，随着预测，图片尺度变大，内容由粗糙到精细。
VAR借鉴了人类通常以分层方式感知或创建图像的本能，即先捕捉全局信息，再处理局部细节；这种多尺度、从粗到细的顺序过程正好与自回归建模需要定义数据顺序相对应，故启发了开发人员即将图像的自回归学习定义为图1©中的“预测下一个尺度”，而不是传统的“预测下一个token”的范式。VAR中，先将图像编码为多尺度token maps，从1×1的token map开始自回归过程，逐渐扩展分辨率，即每一步Transformer基于先前所有的token maps预测下一个更高分辨率的token map。本文贡献如下：

提出一种采用多尺度自回归范式并结合下一尺度预测的新型视觉生成框架，为计算机视觉领域的自回归算法设计提供了新见解；
对 VAR 模型缩放定律及零样本泛化潜力的实证验证，初步模拟了大型语言模型（LLMs）的性能特性；
视觉自回归模型性能的一项突破性进展，首次使 GPT 风格的自回归方法在图像合成任务中超越强大的扩散模型；
一套全面的开源代码套件，涵盖 VQ 分词器和自回归模型训练流程，助力推动视觉自回归学习的发展。

预测下一个token自回归模型范式分析

此范式需要进行类似的分词操作，即先将连续的2D图片数据分割为离散的tokens，然后将其构建为1D的tokens序列。离散这一步往往是通过训练一个VQVAE模型实现，由编码器 $ $\mathcal{E}$ 、量化器 $\mathcal{Q}$ 、解码器 $\mathcal{D}$ 和码本器 $\mathcal{Z} \in \mathbb{R}^{V \times C}$ 组成。编码器将图片转换为固定尺寸的特征图 $\in \mathbb{R}^{h \times w \times C}$ ，量化器将 $f$ 与码本中的向量进行相似度对比装起转换为离散的tokens $\in [V]^{h \times w}$ 。此时 $q$ 仍是二维网格排列，还不是一维序列。图像tokens顺序必须为单向自回归学习显示定义，常规的自回归方法使用光栅扫描、螺旋扫描或Z曲线排序等策略将 $q$ 展平为一维序列 $(x_1,\cdot\cdot\cdot,x_{h \times w})$ ，然后通过预测写一个token进行自回归训练。此种图片生成模型有以下不足：

数学前提违规：在VQVAE中，编码器通常生成图像特征图 $f$ ，其中所有位置 $(i, j)$ 的特征向量 $f^{(i,j)}$ 存在相互依赖关系。因此，经过量化和扁平化处理后，token序列 $(x_1,\cdot\cdot\cdot,x_{h \times w})$ 仍保留双向相关性。这与自回归模型的单向依赖假设相矛盾 —— 该假设要求每个token $x_t$ 仅依赖于其前缀序列 $(x_1,x_2\cdot\cdot\cdot,x_{t-1})$ ;
无法执行某些零样本泛化：与问题 1 类似，图像自回归建模的单向性限制了其在需要双向推理任务中的泛化能力。例如，给定图像的底部时，模型无法预测其顶部内容；
结构退化：扁平化处理破坏了图像特征图中固有的空间局部性。例如，token $q^{(i,j)}$ 与其 4 个直接相邻token $q^{(i\pm1,j)}$ 、 $q^{(i,j\pm1)}$ 因空间邻近而具有紧密相关性。但这种空间关系在一维序列 $x$ 中被削弱 —— 单向约束会降低这些相关性；
效率低下：使用传统自注意力 Transformer 生成图像token序列 $(x_1,x_2,\cdot\cdot\cdot,x_{n \times n})$ 时，需经历 $O(n^2)$ 次自回归步骤，计算成本高达 $O(n^6)$ 。