二分搜索详解-优快云博客

文章目录

在本教程中，您将学习二分搜索排序的工作方式。此外，您还将找到C语言的示例。
二分搜索是一种搜索算法，用于在排序数组中查找元素的位置。
在这种方法中，总是在部分数组的中间搜索元素。
二分搜索只能在已排序的列表上实现。如果元素还没有排序，我们需要先对它们排序。

二分搜索如何工作？

二分搜索算法可以通过以下两种方式实现。

迭代法
递归法

递归方法遵循分治方法。
下面讨论这两种方法的步骤。

待搜索的数组是：

假设 x = 4是要搜索的元素。
在最低和最高位置分别设置两个指针 low 和 high。
找到数组的中间元素 mid，例如 arr[(low + high)/2] = 6。
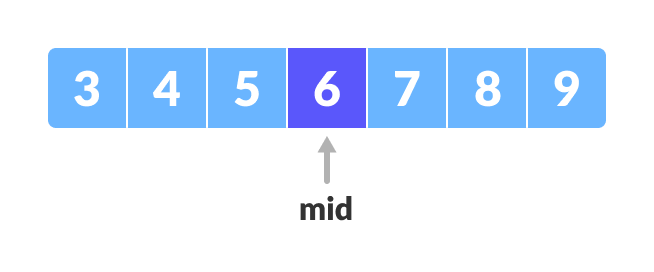
如果x == mid，则返回mid，否则将要搜索的元素与mid进行比较。
如果x>mid，则将x与mid右侧元素的中间元素进行比较。这可以通过将low设置为low=mid+1来完成。
否则，将x与mid左侧元素的中间元素进行比较。这可以通过将high设置为high=mid-1来完成。
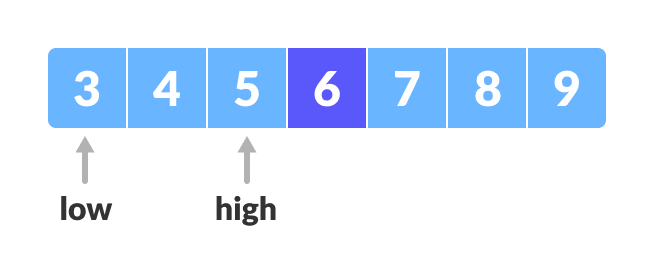
重复步骤3到6，直到 low 遇到 high。
找到 x = 4。

二分搜索伪代码

迭代法

do until the pointers low and high meet each other.
    mid = (low + high)/2
    if (x == arr[mid])
        return mid
    else if (x > arr[mid]) // x is on the right side
        low = mid + 1
    else                       // x is on the left side
        high = mid - 1

递归法

binarySearch(arr, x, low, high)
    if low > high
        return False 
    else
        mid = (low + high) / 2 
        if x == arr[mid]
            return mid
        else if x < arr[mid]        // x is on the right side
            return binarySearch(arr, x, mid + 1, high)
        else                               // x is on the right side
            return binarySearch(arr, x, low, mid - 1)

C示例

迭代法

// Binary Search in C

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high) {
  // Repeat until the pointers low and high meet each other
  while (low <= high) {
    int mid = low + (high - low) / 2;

    if (array[mid] == x)
      return mid;

    if (array[mid] < x)
      low = mid + 1;

    else
      high = mid - 1;
  }

  return -1;
}

int main(void) {
  int array[] = {3, 4, 5, 6, 7, 8, 9};
  int n = sizeof(array) / sizeof(array[0]);
  int x = 4;
  int result = binarySearch(array, x, 0, n - 1);
  if (result == -1)
    printf("Not found");
  else
    printf("Element is found at index %d", result);
  return 0;
}

递归法

// Binary Search in C

#include <stdio.h>

int binarySearch(int array[], int x, int low, int high) {
  if (high >= low) {
    int mid = low + (high - low) / 2;

    // If found at mid, then return it
    if (array[mid] == x)
      return mid;

    // Search the left half
    if (array[mid] > x)
      return binarySearch(array, x, low, mid - 1);

    // Search the right half
    return binarySearch(array, x, mid + 1, high);
  }

  return -1;
}

int main(void) {
  int array[] = {3, 4, 5, 6, 7, 8, 9};
  int n = sizeof(array) / sizeof(array[0]);
  int x = 4;
  int result = binarySearch(array, x, 0, n - 1);
  if (result == -1)
    printf("Not found");
  else
    printf("Element is found at index %d", result);
}