数据结构与算法【二叉搜索树】Java实现

已于 2023-11-20 19:52:06 修改
阅读量248 收藏 2
点赞数 1
CC 4.0 BY-SA版权
文章标签： java 算法 数据结构
于 2023-11-19 21:26:53 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/zmbwcx/article/details/134496000

 介绍

二叉搜索树（也称二叉排序树）是符合下面特征的二叉树：

  1. 树节点增加 key 属性，用来比较谁大谁小，key 不可以重复
  2. 对于任意一个树节点，它的 key 比左子树的 key 都大，同时也比右子树的 key 都小

查找、插入、删除的时间复杂度与树高相关

  • 如果这棵树左右平衡，那么时间复杂度均是 O(logN)
  • 这棵树如果左右高度相差过大，那么这时是最糟的情况，相当于线性查找。时间复杂度是 O(N)。

普通二叉搜索树

public class BSTree<K extends Comparable<K>, V> {
    public BSNode<K, V> root;

    static class BSNode<K, V> {
        K key;
        V value;
        BSNode<K, V> left;
        BSNode<K, V> right;

        public BSNode(K key) {
            this.key = key;
        }

        public BSNode(K key, V value) {
            this.key = key;
            this.value = value;
        }

        public BSNode(K key, V value, BSNode<K, V> left, BSNode<K, V> right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
}

实现通过key获取值

public V get(K key) {
    BSNode<K, V> node = root;
    while (node != null) {
        //当传过来的key为null时会报错
        int result = key.compareTo(node.key);
        if (result < 0) {
            //说明key<node.key
            node = node.left;
        } else if (result > 0) {
            node = node.right;
        } else {
            return node.value;
        }
    }
    return null;
}

实现获取最小key的值

任何节点的左孩子一定比该节点小，因此当遍历到没有左孩子时说明是key最小的节点

public V min() {
    if (root == null) {
        return null;
    }
    BSNode<K, V> node = root;
    while (node.left != null) {
        node = node.left;
    }
    return node.value;
}

实现获取最大key的值

任何节点的右孩子一定比该节点大，因此当遍历到没有右孩子时说明是key最大的节点

public V max() {
    if (root == null) {
        return null;
    }
    BSNode<K, V> node = root;
    while (node.right != null) {
        node = node.right;
    }
    return node.value;
}

实现新增节点

如果key在二叉搜索树中不存在时，进行新增，如果存在则进行值覆盖

public void put(K key, V value) {
    BSNode<K, V> node = root;
    BSNode<K, V> parent = null;
    int result = 0;
    while (node != null) {
        parent = node;
        result = key.compareTo(node.key);
        if (result < 0) {
            //说明key<node.key
            node = node.left;
        } else if (result > 0) {
            node = node.right;
        } else {
            //如果存在该节点就覆盖
            node.value = value;
            return;
        }
    }

    //说明此时没有节点
    if (parent == null){
        root = new BSNode<K,V>(key,value);
    }else if (result<0){
        parent.left = new BSNode<K, V>(key, value);
    }else {
        parent.right = new BSNode<K, V>(key, value);
    }
}

实现获取前驱节点

最简单的实现方式，是进行一次中序遍历，这样可以直接到获取一个升序的排序结果。但是效率较差，因此我们采用别的实现方案。

找前驱节点，可以根据两个规律去实现

  • 节点有左子树，此时前驱节点就是左子树的最大值
  • 节点没有左子树，若离它最近的祖先自从左而来，此祖先即为前驱
public V predecessor(K key) {
    //祖先节点
    BSNode<K, V> ancestorFromLeft = null;
    BSNode<K, V> node = root;
    while (node != null) {
        int result = key.compareTo(node.key);
        if (result < 0) {
            node = node.left;
        } else if (result > 0) {
            //如果进入该分支，说明该节点可以作为一个祖先节点
            ancestorFromLeft = node;
            node = node.right;
        } else {
            break;
        }
    }
    if (node==null){
        //说明没有该节点
        return null;
    }
    //如果存在左孩子
    if (node.left!=null){
        return max(node.left);
    }
    //如果不存在左孩子
    return ancestorFromLeft!=null?ancestorFromLeft.value:null;
}

实现获取后驱节点

与获取前驱节点类似，也可以通过中序遍历拿到排序结果后，寻找指定节点的后驱节点。也可以通过以下两个规律来实现

  • 节点有右子树，此时后继节点即为右子树的最小值
  • 节点没有右子树，若离它最近的祖先自从右而来，此祖先即为后继
public V successor(K key){
    //祖先节点
    BSNode<K, V> ancestorFromLeft = null;
    BSNode<K, V> node = root;
    while (node != null) {
        int result = key.compareTo(node.key);
        if (result < 0) {
            //如果进入该分支，说明该节点可以作为一个祖先节点
            ancestorFromLeft = node;
            node = node.left;
        } else if (result > 0) {
            node = node.right;
        } else {
            break;
        }
    }
    if (node==null){
        //说明没有该节点
        return null;
    }
    //如果存在左孩子
    if (node.right!=null){
        return min(node.right);
    }
    //如果不存在左孩子
    return ancestorFromLeft!=null?ancestorFromLeft.value:null;
}

实现删除指定节点

删除节点比较麻烦。需要考虑4种情况

  • 被删除节点只存在左孩子
  • 被删除节点只存在右孩子
  • 被删除节点是根节点
  • 被删除节点存在两个孩子节点

前两种情况可以通过被删除节点的父结点来继承被删除节点的子节点来实现。而后两种情况则需要找到被删除节点的后驱节点来顶替被删除节点的位置

    public V delete(K key) {
        //找到被删除节点
        BSNode<K, V> deleteNode = root;
        //找到被删除节点的父结点
        BSNode<K, V> parent = null;
        while (deleteNode != null) {
            int result = key.compareTo(deleteNode.key);
            if (result < 0) {
                //说明key<node.key
                parent = deleteNode;
                deleteNode = deleteNode.left;
            } else if (result > 0) {
                parent = deleteNode;
                deleteNode = deleteNode.right;
            } else {
                break;
            }
        }
        if (deleteNode == null) {
            //没找到该节点
            return null;
        }
        //当要删除的节点只存在左节点时
        if (deleteNode.right == null) {
            shift(parent, deleteNode, deleteNode.left);
        } else if (deleteNode.left == null) { //当要删除的节点只存在右节点时
            shift(parent, deleteNode, deleteNode.right);
        } else { //当要删除的节点存在两个子节点时，需要找到要删除节点的后驱节点
            //后驱节点
            BSNode<K, V> s = deleteNode.right;
            //后驱节点的父亲节点。用来判断被删除的节点与其后驱节点是否相邻
            BSNode<K, V> sParent = null;
            while (s.left != null) {
                sParent = s;
                s = s.left;
            }
            //如果要删除的节点与后驱节点不相邻
            if (sParent != deleteNode) {
                //将后驱节点的子节点交给后驱节点的父结点
                shift(sParent, s, s.right);
                //后驱节点接管被删除节点的右孩子
                s.right = deleteNode.right;
            }
            //如果要删除的节点与后驱节点相邻
            shift(parent,deleteNode,s);
            //后驱节点顶替被删除节点的位置
            s.left = deleteNode.left;
        }
        return deleteNode.value;
    }

    /**
     * 将要删除的节点的子节点转移到其父结点上
     *
     * @param parent     父结点
     * @param deleteNode 要删除的节点
     * @param child      子节点
     */
    private void shift(BSNode<K, V> parent, BSNode<K, V> deleteNode, BSNode<K, V> child) {
        if (parent == null) {
            //说明要删除的节点为根节点
            root = child;
        } else if (deleteNode.left == child) {
            //如果要删除的节点只存在左节点
            parent.left = child;
        }else {
            parent.right = child;
        }
    }

实现范围查询

采用中序遍历得到排序结果后，将符合范围的节点返回一个集合

//查找小于key的所有节点的value
public List<V> less(K key) {
    List<V> result = new ArrayList<>();
    LinkedList<BSNode<K, V>> linked = new LinkedList<>();
    BSNode<K, V> node = root;
    while (node != null || !linked.isEmpty()) {
        if (node != null) {
            linked.push(node);
            node = node.left;
        } else {
            BSNode<K, V> pop = linked.pop();
            int compare = key.compareTo(pop.key);
            //如果比指定值小
            if (compare > 0) {
                //加入列表
                result.add(pop.value);
            } else {
                //如果比指定值大，没有接着循环的必要
                break;
            }
            node = pop.right;
        }
    }
    return result;
}

可以自己实现一下>key或是k1<=values<=k2的代码。

平衡二叉搜索树

如果普通二叉搜索树不平衡的情况下，最坏情况下查询与线性查询没有区别。如下图所示

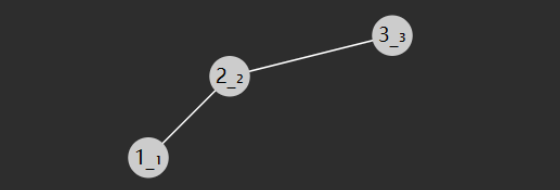
因此，我们可以通过旋转来使一棵不平衡的二叉树变得平衡

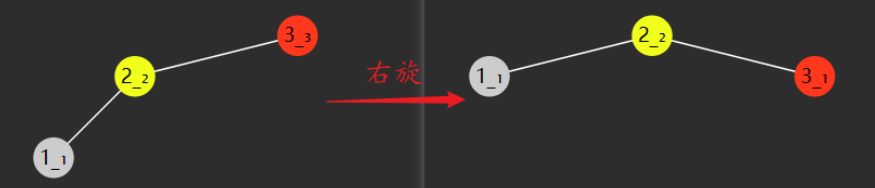
失衡条件

如果一个节点的左右孩子，高度差超过 1，则此节点失衡，才需要旋转

解决方法

失衡存在以下四种情况：

LL：失衡节点的左子树更高（L），失衡节点的左孩子的左子树等高或更高（L）

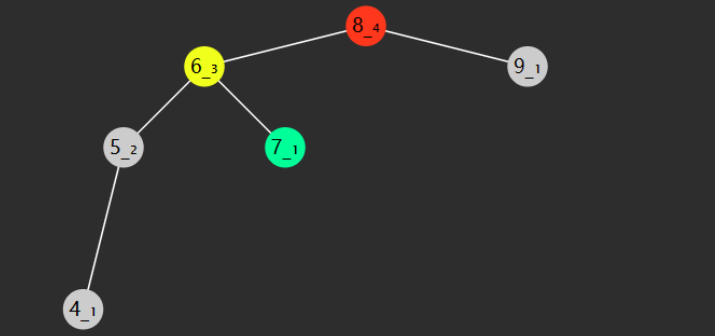
LR：失衡节点的左子树更高（L），失衡节点的左孩子的右子树更高（R）

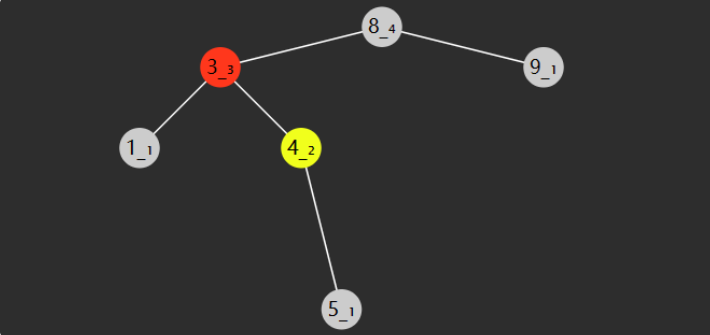
RL：失衡节点的右子树更高（R），失衡节点的右孩子的左子树更高（L）

RR：失衡节点的右子树更高（R），失衡节点的右孩子的右子树等高或更高（R）

这四种情况对应的旋转情况如下

  • LL：失衡节点右旋
  • LR：失衡节点的左子树左旋，之后失衡节点右旋（又叫左右旋）
  • RL：失衡节点的右子树右旋，之后失衡节点左旋（又叫右左旋）
  • RR：失衡节点右旋

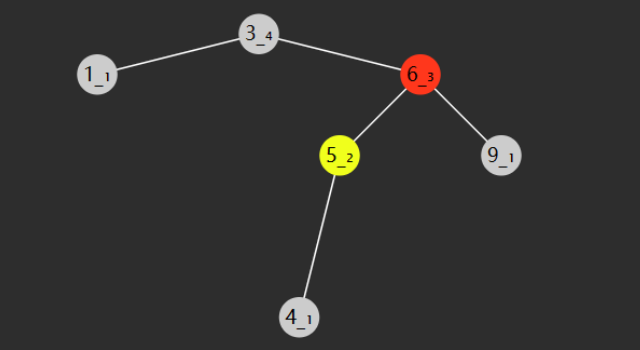
左右旋示例

这是一个不平衡的二叉搜索树 

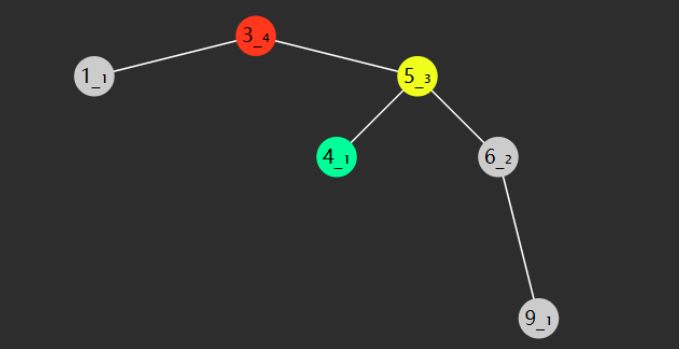
左子树旋转后

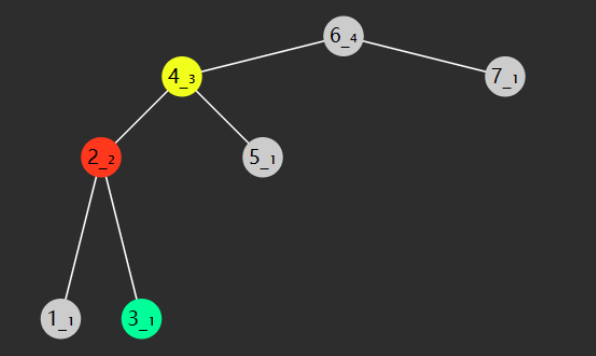
失衡节点右旋

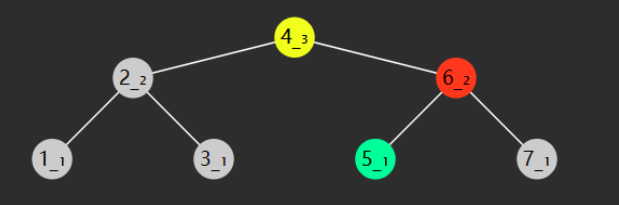
实现代码

大体框架

相比普通二叉搜索树，需要添加一个新的属性height来记录当前节点高度

public class AVLTree {

    private AVLNode root;

    static class AVLNode {
        //树高度
        int height = 1;
        int key;
        Object value;
        AVLNode left;
        AVLNode right;

        public AVLNode(int key, Object value) {
            this.key = key;
            this.value = value;
        }

        public AVLNode(int key, Object value, AVLNode left, AVLNode right) {
            this.key = key;
            this.value = value;
            this.left = left;
            this.right = right;
        }
    }
}

高度查询及更新代码

//获取高度
private int height(AVLNode node) {
    return node == null ? 0 : node.height;
}

//更新高度。寻找子节点中较大的高度急+1即可
private void updateHeight(AVLNode node) {
    node.height = Integer.max(height(node.left), height(node.right)) + 1;
}

//判断是否失衡。如果返回值为1、0、-1表示没有失衡
private int bf(AVLNode node) {
    return height(node.left) - height(node.right);
}

结点旋转代码

/**
 * 将指定节点右旋后返回新的父结点
 *
 * @param node
 * @return
 */
public AVLNode rightRotate(AVLNode node) {
    //要被旋转的节点去拿到新父节点的右孩子
    AVLNode newParent = node.left;
    node.left = newParent.right;
    newParent.right = node;
    //旋转过后需要修改节点高度。
    //注意！必须先修改失衡节点。
	//因为在旋转后，失衡节点高度会下降，底层节点正确后才能更新上层节点
    updateHeight(node);
    updateHeight(newParent);
    return newParent;
}

/**
 * 将指定节点左旋后返回新的父结点
 *
 * @param node
 * @return
 */
public AVLNode leftRotate(AVLNode node) {
    //要被旋转的节点去拿到新父节点的右孩子
    AVLNode newParent = node.right;
    node.right = newParent.left;
    newParent.left = node;
    updateHeight(node);
    updateHeight(newParent);
    return newParent;
}

/**
 * 左右旋后返回新的父结点
 *
 * @param node
 * @return
 */
public AVLNode leftRightRotate(AVLNode node) {
    //修改要被旋转节点的左孩子节点，相当于左旋左子树
    node.left = leftRotate(node.left);
    //右旋失衡节点
    return rightRotate(node);
}


/**
 * 右左旋后返回新的父结点
 *
 * @param node
 * @return
 */
public AVLNode rightLeftRotate(AVLNode node) {
    //修改要被旋转节点的右孩子节点，相当于右旋右子树
    node.right = rightRotate(node.right);
    //左旋失衡节点
    return leftRotate(node);
}

判断节点是否失衡代码

/**
 * 判断节点是否失衡
 * @param node
 * @return
 */
public AVLNode balance(AVLNode node){
    if (node == null){
        return null;
    }
    int bf = bf(node);
    //如果失衡节点的左子树高，此时属于L
    if (bf>1){
        if (bf(node.left)>=0){
            //此时属于LL
            return rightRotate(node);
        }else {
            //此时属于LR
            return leftRightRotate(node);
        }
    }else if (bf<-1){//此时属于R
        if (bf(node.right)>=0){
            //此时属于RR
            return leftRotate(node);
        }else {
            //此时属于RL
            return rightLeftRotate(node);
        }
    }
    //不失衡，直接返回
    return node;
}

新增节点代码

/**
 * 新增节点
 * @param key
 * @param value
 */
public void put(int key, Object value) {
    root = doPut(root, key, value);
}

private AVLNode doPut(AVLNode node, int key, Object value) {
    if (node == null) {
        return new AVLNode(key, value);
    }
    if (key == node.key) {
        node.value = value;
        return node;
    }
    if (key < node.key) {
        node.left = doPut(node.left, key, value);
    } else {
        node.right = doPut(node.right, key, value);
    }
    //更新高度
    updateHeight(node);
    //判断是否失衡
    return balance(node);
}

删除节点代码

/**
 * 删除节点
 * @param key
 * @return
 */
public void remove(int key) {
    root = doRemove(root, key);
}

private AVLNode doRemove(AVLNode node, int key) {
    if (node == null) {
        return null;
    }
    if (key < node.key) {
        node.left = doRemove(node.left, key);
    } else if (node.key < key) {
        node.right = doRemove(node.right, key);
    } else {
        //找到要删除的节点了
        if (node.left == null) {
            //如果左边为null。那么右边节点顶替被删除节点
            node = node.right;
        } else if (node.right == null) {
            //如果右边为空，那么左边节点顶替被删除节点
            node = node.left;
        } else {
            //如果均不为null。那么找到后驱节点
            AVLNode s = node.right;
            while (s.left != null) {
                s = s.left;
            }
            //后驱节点的右孩子为被删除节点的右孩子
            s.right = doRemove(node.right, s.key);
            s.left = node.left;
            //将后驱节点替代被删除节点
            node = s;
        }
    }
    updateHeight(node);
    return balance(node);
}

总结

AVL树的优点：

  1. AVL树是一种自平衡树，保证了树的高度平衡，从而保证了树的查询和插入操作的时间复杂度均为O(logn)。
  2. 相比于一般二叉搜索树，AVL树对查询效率的提升更为显著，因为其左右子树高度的差值不会超过1，避免了二叉搜索树退化为链表的情况，使得整棵树的高度更低。
  3. AVL树的删除操作比较简单，只需要像插入一样旋转即可，在旋转过程中树的平衡性可以得到维护。

AVL树的缺点：

  1. AVL树每次插入或删除节点时需要进行旋转操作，这个操作比较耗时，因此在一些应用中不太适用。
  2. 在AVL树进行插入或删除操作时，为保持树的平衡需要不断进行旋转操作，在一些高并发环节和大数据量环境下，这可能会导致多余的写锁导致性能瓶颈。
  3. AVL树的旋转操作相对较多，因此在一些应用中可能会造成较大的空间浪费。

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

zmbwcx2003

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值