常见的链表操作

一、单链表

      单链表的操作主要包括：链表数据插入、删除节点，以及一些衍生的单链表的翻转、检测链表中的环、两个有序链表的合并、删除倒数第n个节点和求链表的中间节点。

      首先是单链表的基本操作：链表的插入，在这里使用的是头插法，并且添加了哨兵节点，也就是头结点，这样可以不用考虑头结点的边界问题，具体C++代码如下：

    1、链表的插入

struct SingleListNode
{
	int data;
	struct SingleListNode* next;

	// 默认构造函数
	SingleListNode(int data):data(data),next(nullptr){}
	SingleListNode():next(nullptr){}
};


// 使用的头插法
int insert_node(SingleListNode* pHead, int data)
{
	SingleListNode* pNode = new SingleListNode();
	if (pNode == NULL)
	{
		return -1;
	}

	pNode->data = data;
	// 若没有数据
	if(pHead->next == nullptr)
	{
		pHead->next = pNode;
	}
	else
	{
		// 从头开始往后插入
		pNode->next = pHead->next;
		pHead->next = pNode;
	}
	return 0;
}

 

    2、指定节点删除

/*
	移除某一个特定节点，该节点在链表中，其中该链表是带哨兵节点的单链表
	这样可以不用考虑头节点问题。
*/ 
void remove_node(SingleListNode* pHead, SingleListNode* pNode)
{
	if(pHead->next == nullptr || pNode == nullptr)
	{
		return;
	}

	// 去除的删除尾节点
	if(pNode->next == nullptr)
	{
		SingleListNode* pre = pHead->next;
		while (pre->next != pNode)
		{
			pre = pre->next;
		}
		pre->next = pNode->next;
		delete pNode;
		pNode = nullptr;
	}
	else
	{
		// 将下一个节点的值赋给待删除的节点
		pNode->data = pNode->next->data;
		SingleListNode* t_node = pNode->next;
		pNode->next = pNode->next->next;
		delete t_node;
		t_node = nullptr;
	}
}

// 删除某一个特定值
void remove_node(SingleListNode* pHead, int data)
{
	if(pHead->next == nullptr) return;
	SingleListNode* pcur = pHead;
	SingleListNode* pre = nullptr;

	while (pcur != nullptr)
	{
		pre = pcur;
		pcur = pcur->next;
		if(pcur->data == data)
			break;
	}
	// 如果是尾节点
	if (pcur->next == nullptr)
	{
		pre->next = nullptr;
	}
	else
	{
		pre->next = pcur->next;
	}
	delete pcur;
	pcur = nullptr;
	return;
}

二、双链表 

      双链表是在单链表的基础上多了一个前向指针，用于指向前一个节点，这样做的好处是，可以随时知道自己的前一个节点是谁，并且可利用双链表实现LRU缓存淘汰算法。

    1、数据插入

       代码实现使用的是头插法，并且记录头节点和尾节点，这样可以方便的定位尾节点，并且添加节点计数器，可以通过计数器来判断链表是否为空。

// 用于存储数据结点
typedef struct DlistNode
{
	struct DlistNode *prev;
	struct DlistNode *next;
	int data;
}stDlistNode;

// 存储尾结点和头节点
typedef struct Dlisthead
{
	stDlistNode *tail;
	stDlistNode *head;
	int size;
}stDlistHead;


/*
	初始化
*/
void dlist_init(stDlistHead *dlist)
{
	dlist->head = NULL;
	dlist->tail = NULL;
	dlist->size = 0;
	return;
}

/*在链表中插入数据*/
int dlist_insert_head(stDlistHead *dlist, stDlistNode* pNode, int data)
{
	// 申请节点内存
	if(pNode == NULL)
	{
		pNode = (stDlistNode*)malloc(sizeof(stDlistNode));
		if(pNode == NULL)
			return -1;
	}
	// 赋值
	pNode->data = data;
	pNode->next = NULL;
	pNode->prev = NULL;

	// 若当前没有结点
	if(dlist->size == 0)
	{
		dlist->head = pNode;
		dlist->tail = pNode;
	}
	else
	{
		// 从头往后开始插入数据
		pNode->next = dlist->head;
		dlist->head->prev = pNode;
		dlist->head = pNode;
	}
	dlist->size++;
	return 0;
}

    2、移除节点

         移除尾节点的代码实现如下

/*
	三种情况：一是没有结点、有一个结点和多个结点
*/
stDlistNode* dlist_remove_tail(stDlistHead* dlist)
{
	stDlistNode* pNode = NULL;
	// 若没有结点，则返回空
	if(dlist->size == 0) return NULL;

	pNode = dlist->tail;
	// 超过一个结点，将尾结点的前一个结点作为尾结点
	if(dlist->size > 1)
	{
		dlist->tail = dlist->tail->prev;
		dlist->tail->next = NULL;
	}
	else
	{
		// 如果只有一个结点，那么就清空节点
		dlist->tail = NULL;
		dlist->head = NULL;
	}
	dlist->size--;
	return pNode;
}

          删除某一个节点代码如下，待删除节点是特定节点，无需遍历链表寻找节点位置

// 移除某一个结点
void dlist_remove_node(stDlistHead * dlist,stDlistNode *pNode)
{
	if (dlist == NULL || pNode == NULL)
	{
		return;
	}
	// 去除的是头结点，则将下一个结点设为头结点
	if(dlist->head == pNode)
	{
		dlist->head = dlist->head->next;
	}
	else if(dlist->tail == pNode)
	{
		// 如果去除的是尾结点，则前一个结点设为尾结点
		dlist->tail =pNode->prev;
		dlist->tail->next = NULL;
	}
	else
	{
		// 若是一般结点
		pNode->prev->next = pNode->next;
		pNode->next->prev = pNode->prev;
	}
	// 删除节点
	dlist->size--;
	pNode->prev = NULL;
	pNode->next = NULL;

	// 没有结点，那么初始化为0
	if(dlist->size == 0)
	{
		memset(dlist, 0, sizeof(stDlistHead));
	}
	return;
}

    3、寻找某一个节点

         根据给定的data，遍历链表，找到该节点

// 寻找某一个结点
stDlistNode* dlist_search_node(stDlistHead * dlist,int data)
{
	if(dlist == NULL) return NULL;
	// 头结点
	stDlistNode* pNode = dlist->head;
	while (pNode != NULL)
	{
		if (pNode->data == data)
		{
			return pNode;
		}
		pNode = pNode->next;
	}
	return NULL;
}

    4、LRU缓存算法

      LRU（Least recently used，最近最少使用）算法根据数据的历史访问记录来进行淘汰数据，其核心思想是“如果数据最近被访问过，那么将来被访问的几率也更高”，当限定的空间存满数据时，把最久没有被访问到的数据删除。

      那么利用链表来实现的思路：当需要插入新的数据的时候，如果新数据在链表中已存在，则把该节点移到链表头部即可，如果不存在，则新建一个节点，插到链表头部；若缓存满了，则把链表最后一个节点删除，再插入到链表头结点。这样一来就保持链表尾部的节点就是最近最久未访问的数据项。使用双链表的具体代码实现如下：

// 基于链表的LRU缓存淘汰算法
// 利用上述已经实现的某些函数来实现
void Lru_node(stDlistHead* dlist, int data)
{
	stDlistNode* pNode = NULL;
	// 找到当前值
	pNode = dlist_search_node(dlist, data);
	if(pNode != NULL)
	{
		// 如果当前存在，则删除旧结点
		dlist_remove_node(dlist, pNode);
	}
	else if(dlist->size > 5)
	{
		// 若缓存太多，先删除尾结点，这里设大小是5个
		pNode = dlist_remove_tail(dlist);
	}
	// 将最新的值插入在头结点，利用删除的结点，重新插入到头结点
	dlist_insert_head(dlist, pNode, data);
}

 

 

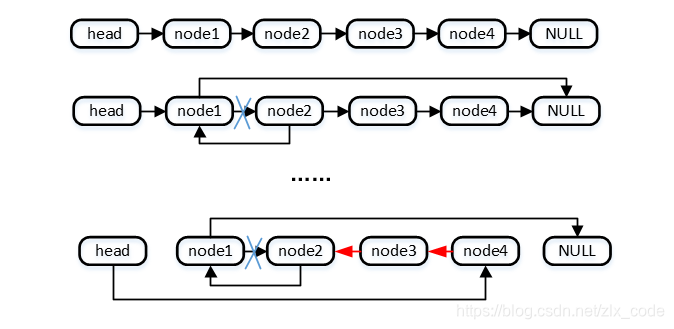
三、单链表反转

       解决思路：每次将后一个节点指向前一个结点，直至最后一个节点，就可以将链表反转，效率高。如下图所示：

                                  

       代码实现如下：需要三个指针前一个节点pre，当前节点pcur，和下一个节点pnext。

/* 单链表的翻转 */
void node_reverse(SingleListNode* pHead)
{
	if(pHead->next == nullptr || pHead->next->next == nullptr)
		return ;

	SingleListNode* pCur = pHead->next;
	SingleListNode* pNext = pCur->next;
	SingleListNode* pre = nullptr;
	while (pNext)
	{
		pCur->next = pre;
		pre = pCur;
		pCur = pNext;
		pNext = pCur->next;
	}
	pCur->next = pre;
	pHead->next = pCur;
	return;
}

 

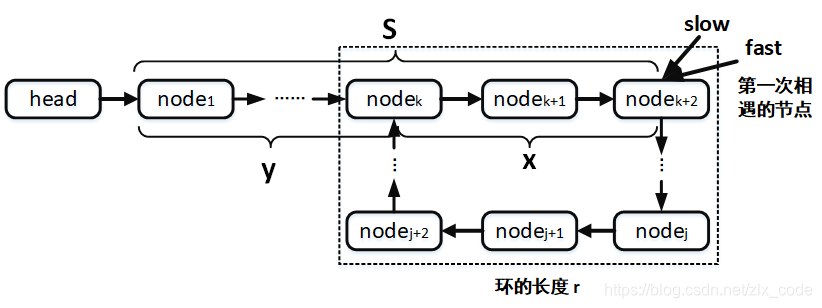
四、两个单链表是否相交，以及环的入口节点

       解救思路：使用两个指针 fast 和 slow，fast每次移动两个节点，slow每次移动一个节点，若链表存在环，那么fast肯定会和slow相遇。代码如下：

/*
	定义两个指针：fast和slow，初始位置都在头指针处
	其中fast每次移动两个节点，slow每次移动一个节点
	若存在环，那么，fast会在环中与slow相遇

*/
bool check_node_circle(SingleListNode* pHead)
{
	// 检查链表
	if(pHead->next == nullptr || pHead->next->next == nullptr){
		return false;
	}
    // 定义两个指针，fast每次移动两个节点，slow每次移动一个节点
	SingleListNode* fast_ptr = pHead->next;
	SingleListNode* slow_ptr = pHead->next;

	while (nullptr != fast_ptr && nullptr != fast_ptr->next){
		fast_ptr = fast_ptr->next->next;
		slow_ptr = slow_ptr->next;
		if (fast_ptr == slow_ptr){
			return true;
		}
	}
	return false;
}

       

      假设链表环长 r，slow走s步与fast相遇，那么fast走了2s步，fast与slow相遇的时候，多走了 n*r圈，因此有：

               2s = s + n*r  ==>  s = n*r， 假设起点到环入口的距离是 y，则  x+y = n*r，

               有 y = n*r - x = (n-1)*r + r -x，从式中看出，当fast移到第一个节点node1，slow还是当前相遇节点，现在fast和           slow每次移动一个节点，那么下次两个节点相遇的时候就是环入口节点，其中slow走了（ n-1圈环 + r-x），而fast走了        y 个节点。 

SingleListNode* find_node_entrance(SingleListNode* pHead)
{
	// 检查链表
	if(pHead->next == nullptr || pHead->next->next == nullptr){
		return nullptr;
	}

	// 指定fast和slow的结点位置
	SingleListNode* fast_ptr = pHead->next;
	SingleListNode* slow_ptr = pHead->next;
	
	// 在环路中找到 fast 与 slow 第一次相遇的地方
	while (fast_ptr != nullptr && fast_ptr->next != nullptr)
	{
		fast_ptr = fast_ptr->next->next;
		slow_ptr = slow_ptr->next;

		// 如果相遇
		if(fast_ptr == slow_ptr){
			// fast移动到头节点
			fast_ptr = pHead->next;
			// 再次相遇
			while (fast_ptr != slow_ptr){
				fast_ptr = fast_ptr->next;
				slow_ptr = slow_ptr->next;
			}
			return fast_ptr;
		}
	}
	return nullptr;
}

    至于求解环的长度，可以先找到当前第一次相遇的节点，然后固定其中一个节点，另外一个以一个步长继续走，下次相遇所前，走过的节点个数就是环的长度；第二种就是fast和slow接着按照当前方式，fast每次两个节点步长，slow一个，下次相遇的时候，所走过的长度就是环的节点个数。