CRF模型——打通crf模型的任督二脉（二）

接着上一篇的讲到的MEMM的问题来说，

MEMM产生Label Bias的根源是什么，
这是因为MEMM的状态转移概率的计算方式，为了获得转移概率，它每一步的状态转移都会进行归一化，从而导致问题的产生。
CRF认清了问题的根源，只要不要在每一步状态转移进行归一化，而在全局进行归一化 就能一下子化解了MEMM产生的Label Bias标注偏好这个大问题。

$p(\vec{s}|\vec{x})={\prod }_{i=0}^{n}p(s_i|s_{i-1},x_1,x_2,...,x_n)={\prod }_{i=0}^n\frac{exp({\vec{w}}^{T}f(s_i,s_{i-1},\vec{x}))}{{\sum }_{s^{{}^{\prime }}\in S}exp({\vec{w}}^{T}f({\vec{s}}^{{}^{\prime }},s_{i-1},\vec{x}))}$

$p(\vec{s}|\vec{x})=\frac{exp({\vec{w}}^T\Phi (\vec{s},\vec{x}))}{{\sum }_{s^{{}^{\prime }}\in S^n}exp({\vec{w}}^T\Phi ({\vec{s}}^{{}^{\prime }},\vec{x}))}$

第一个是MEMM 对条件概率做的表达式，
第二个是CRF 对条件概率做的表达式，
分母中的 $s^{{}^{\prime }}\in S,s^{{}^{\prime }}\in S^n$ 一点点不同，表示的含义就千差万别了，前者只是局部的，后者是全局的。

CRF相对于MEMM做了几个改动，首先在特征函数上面做了变动：
$\Phi (\vec{s},\vec{x})\to R^d$
第一个是它将输入序列$\vec{x}$和输出标注$\vec{s}$映射为一个d维实数向量(这个d其实就是特征函数的个数，联系前面讲到的特征函数的内容，$L\ast N,L\ast L\ast N$)，而MEMM的特征函数拥有的信息只是输入序列$\vec{x}$和当前状态以及上一个状态，也就是说CRF的特征函数掌握信息量更多，从而表达能力更强。

第二个的改进是它不再针对每一次状态转移进行归一化，而是在全局进行归一化，这样完美解决Label Bias问题。

有得必有失，注意到全局进行归一化就意味着 模型的分母需要罗列所有的状态序列，对于序列长度为n的输入序列，状态序列的个数为$|S{|}^n$，对于这种指数增长问题，在实际应用中一般都是intractable的，只能付诸于近似求解，比如我们之前提过的Variational Bayes或者Gibbs Sampling等等。不过有一种特殊结构的CRF，精确快速求解的方式是存在的(前向后向算法帮助我们)，因此在早期得以广泛应用。

下面我们就看CRF中是如何做参数估计，也就是所如何来求各 取值的导数，以及更新的。
这一部分 小蓝书《统计学习方法》上讲的是尤其不好，公式中的字母用的都很泛化，看了几遍都等于白看
好在https://blog.youkuaiyun.com/aws3217150/article/details/68935789这篇博客中，讲的不错，而且 该博客中的推导是和CRF++源码中的代码公式可以一一对应的，参考价值更大，而且一步步推导的过程明晰，特别是如何一步步引出了前向后向算法，也在推导中水到渠成。不过该博客中有一处 的一个字母写错了，我后面会指出。

参数估计

接下来我们介绍对于Linear Chain CRF如何进行参数参数估计的。假设我们有训练集$\overrightarrow{x^1},\overrightarrow{x^2},...,\overrightarrow{x^N}$，对应的标注集合$\overrightarrow{s^1},\overrightarrow{s^2},...,\overrightarrow{s^N}$，那么其对应的对数似然函数为：

$$\begin{gathered} L=\sum _i^{N}logp(\overrightarrow{s^i}|\overrightarrow{x^i}) \\ =\sum _i^{N}log\frac{exp(\overrightarrow{w^T}\Phi (\overrightarrow{s^i},\overrightarrow{x^i}))}{{\sum }_{{\vec{s}}^{{}^{\prime }}\in S^n}exp(\overrightarrow{w^T}\Phi (\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}))} \\ =\sum _i^{N}log\frac{exp({\sum }_k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^i},\overrightarrow{x^i}))}{{\sum }_{{\vec{s}}^{{}^{\prime }}\in S^n}exp({\sum }_k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}))} \\ =\sum _i^{N}log(exp(\sum _k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^i},\overrightarrow{x^i})))-log(\sum _{{\vec{s}}^{{}^{\prime }}\in S^n}exp(\sum _k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}))) \end{gathered}$$

上面公式中要明确$\Phi (\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i})和{\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i})$的区别，$\Phi ()是由多个（L\ast N,L\ast L\ast N）的{\Phi }_k()$的集合表示。 另外每一个 ${\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i})$是每一个特征函数对应的特征值，是每一个特征函数在 ${\sum }_{i=1}^N$的每一个位置上的取值（0或1）求和后得到的。

上式对$w_j$进行求导，前一项很好求，后一项 先是log x的导数为1/x ，然后再链式求导，可得：

$\frac{\partial L}{\partial w_j}={\sum }_i^N{\Phi }_j(\overrightarrow{s^i},\overrightarrow{x^i})-{\sum }_i^N\frac{{\sum }_{{\vec{s}}^{{}^{\prime }}\in S^n}exp({\sum }_k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}){\Phi }_j(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}))}{{\sum }_{{\vec{s}}^{{}^{\prime }}\in S^n}exp({\sum }_k\overrightarrow{w_k}{\Phi }_k(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i}))}$
观察$p(s|x)$的表达式，正好可以凑出一项，

$\frac{\partial L}{\partial w_j}={\sum }_i^N{\Phi }_j(\overrightarrow{s^i},\overrightarrow{x^i})-{\sum }_i^N{\sum }_{{\vec{s}}^{{}^{\prime }}\in S^n}p({\vec{s}}^{{}^{\prime }}|x^i){\Phi }_j(\overrightarrow{s^{{}^{\prime }}},\overrightarrow{x^i})$

上面的式子还不可编程，问题出现在上面减号的右半部分，我们单独讨论(为了记号方便，我们省去上标i)，即表示为：
${\sum }_{\vec{s}\in S^n}p(\vec{s}|x){\Phi }_j(\vec{s},\vec{x})$
正如我们上面讲的，${\Phi }_j(\vec{s},\vec{x})$ 表示的是第j个特征函数值，它是由特征函数${\varphi }_j$在${\sum }_{i=1}^N$的每一个位置上的取值（0或1）求和后得到的。所以上面的如果需要编码，需要进一步写成，下面的形式：

$$\begin{gathered} \sum _{\vec{s}\in S^n}p(\vec{s}|x){\Phi }_j(\vec{s},\vec{x}) \\ \sum _{\vec{s}\in S^n}p(\vec{s}|x)\sum _k{\varphi }_j(s_{k-1},s_k,\vec{x}) \\ \sum _k\sum _{\vec{s}\in S^n}p(\vec{s}|x){\varphi }_j(s_{k-1},s_k,\vec{x}) \\ \sum _k\sum _{a\in S,b\in S}{\varphi }_j(s_{k-1}=a,s_k=b,\vec{x})\sum _{\vec{s}\in S^n,s_{k-1}=a,s_k=b}p(\vec{s}|x) \end{gathered}$$

上面的这个转换，推导其实是很重要的，也是推向前向后向的基础，
上述转换，推导中 从 $\vec{s}\in S^n$ 到$s_{k-1}=a,s_k=b,a\in S,b\in S$ 这个退化很重要，因为 CRF的特征函数只会最多用到 了 前后两个位置，所以可以这样转换，推导。

现在问题在于对于任意a,b我们是否能快速求解 出：

$$\begin{gathered} \sum _{\vec{s}\in S^n,s_{k-1}=a,s_k=b}p(s_1,s_2,...,s_{i-1},s_i,...,s_n|x) \\ =\sum _{\vec{s}\in S^n,s_{k-1}=a,s_k=b}p(s_1,s_2,...,s_{k-1},s_k,...,s_n|x) \\ =p(s_{k-1}=a,s_k=b|x) \end{gathered}$$

这里，不知不觉就已经推导出了边缘概率$p(s_{k-1}=a,s_k=b|x)$的由来了。
所以这里就水到渠成地该讲到Forward-Backward 算法了。

Forward-Backward 算法

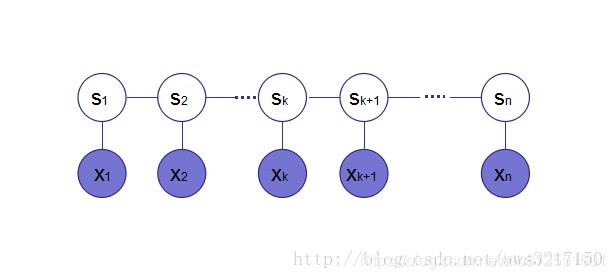
首先对于如下概率图模型：

根据定义，我们可得：

$p(\vec{s}|\vec{x})=\frac{exp({\vec{w}}^T\Phi (\vec{s},\vec{x}))}{{\sum }_{s^{{}^{\prime }}\in S^n}exp({\vec{w}}^T\Phi ({\vec{s}}^{{}^{\prime }},\vec{x}))}=\frac{\psi (\vec{s},\vec{x})}{\psi (\vec{x})}$。
后面的$\psi (\vec{s},\vec{x}),\psi (\vec{x})$是我们定义的，

这里值得注意的是三个符号$\Phi (\vec{x})、\varphi (\vec{x})、\psi (\vec{x})$的含义都是不一样的，
$\Phi (\vec{x})$是特征函数对应的特征值的集合
$\varphi (\vec{x})$是某个特征函数对应的特征值
$\psi (\vec{x})$是特征函数对应的特征值乘以对应的权重参数$w$之后的值,再指数化。

因此上面式子的分母：
$$\begin{gathered} \psi (\vec{x})=\sum _{s^{{}^{\prime }}\in S^n}exp({\vec{w}}^T\Phi ({\vec{s}}^{{}^{\prime }},\vec{x})) \\ \sum _{s^{{}^{\prime }}\in S^n}exp(\sum _k{w}_k\sum _j\varphi (s_{j-1},s_j,\vec{x})) \\ \sum _{s^{{}^{\prime }}\in S^n}exp(\sum _j\sum _k{w}_k\varphi (s_{j-1},s_j,\vec{x})) \\ \sum _{s^{{}^{\prime }}\in S^n}\prod _{j}exp(\sum _k{w}_k\varphi (s_{j-1},s_j,\vec{x})) \end{gathered}$$
上面的最后一步推导很重要，正因为有最后一步推导中的连乘符号，才和我们熟悉 前后向算法的中的连乘符号对应起来了。
我们再抽象出一个定义来，$\psi (s_{j-1},s_j)=exp({\sum }_k{w}_k\varphi (s_{j-1},s_j,\vec{x}))$.
其实 这样定义的
$\psi (s_{j-1},s_j)$ 就是链式CRF模型中常说的因子，这个概念了。这样一步步推导过来，也很自然。$s_{j-1},s_j$是图中的前后两个位置，也是其最大团，最大clique？

因此，
$$\begin{gathered} \psi (\vec{x})=\sum _{s^{{}^{\prime }}\in S^n}\prod _j\psi (s_{j-1},s_j) \\ =\sum _{s_1}\sum _{s_2}...\sum _{s_n}\prod _j\psi (s_{j-1},s_j) \\ =\sum _{s_1}\sum _{s_2}...\sum _{s_n}\psi (s_0=\ast ,s_1)\psi (s_1,s_2)...\psi (s_{n-1},s_n)\psi (s_n,s_{n+1}=STOP) \\ =[\sum _{s_n}\psi (s_n,STOP)[\sum _{s_{n-1}}\psi (s_{n-1},s_n)...[\sum _{s_1}\psi (s_1,s_2)[\psi (\ast ,s_1)]]...]] \end{gathered}$$

自然想到迭代的应用，
如果定义，
$\alpha (s_k)=[{\sum }_{s_{k-1}}\psi (s_{k-1},s_k)[{\sum }_{s_{k-2}}\psi (s_{k-2},s_1)...[{\sum }_{s_1}\psi (s_1,s_2)[\psi (\ast ,s_1)]]...]]$

则 容易有下面的动态规划方程的递推式：
$\alpha (s_k)={\sum }_{s_{k-1}}\psi (s_{k-1},s_k)\alpha (s_{k-1})$

那么，这样就有：
$\psi (\vec{x})=\alpha (s_{n+1})={\sum }_{S_n}\psi (s_n,STOP)\alpha (s_n)$

该动态规划方程的递推式便是前后向算法的forward阶段（前向阶段），其初始值定义为：
$\alpha (s_1)=\psi (\ast ,s_1)$

若上述的前向过程，用重新实现，伪代码如下：

# n为序列x的长度
for s in S:
    alpha(1,s) = psi(*,s)  ##1表示第一轮，该轮的终点是s,起始是*（一种选择）
for(m = 2; m <= n; m++):
    for s in S:
        for s' in S:
            alpha(m, s) += psi(s', s) * alpha(m-1, s') ##m表示第m轮，该轮的终点是s,起始是 s'（s种选择）,把起始的s种选择的结果相加后才是alpha(m, s) 
for s in S:
    alpha(n+1, STOP) += psi(s, STOP) * alpha(n, s)##n+1表示第n+1轮，该轮的终点是stop(1种选择),起始是 s'（s种选择）,把起始的s种选择的结果相加后才是alpha(n+1, STOP) ，

最终的$\alpha (n+1,STOP)$ 就是$\psi (\vec{x})$。 也就是整个式子，用于求边缘概率的分母。

类似的反向的backward阶段。
反向的推导是
$$\begin{gathered} \psi (\vec{x})=\sum _{s^{{}^{\prime }}\in S^n}\prod _j\psi (s_{j-1},s_j) \\ =\sum _{s_1}\sum _{s_2}...\sum _{s_n}\prod _j\psi (s_{j-1},s_j) \\ =\sum _{s_1}\sum _{s_2}...\sum _{s_n}\psi (s_0=\ast ,s_1)\psi (s_1,s_2)...\psi (s_{n-1},s_n)\psi (s_n,s_{n+1}=STOP) \\ =[\sum _{s_1}\psi (\ast ,s1)[\sum _{s_2}\psi (s_1,s_2)...[\sum _{s_{n-1}}\psi (s_{n-1},s_n)[\psi (s_n,STOP)]]...]] \end{gathered}$$

同样的，如果定义，
$\beta (s_k)=[{\sum }_{s_{k+1}}.\psi (s_k,s_{k+1})...[{\sum }_{s_{n-1}}\psi (s_{n-2},s_{n-1})[{\sum }_{s_n}\psi (s_{n-1},s_n)[\psi (s_n,STOP)]]]...]$

则 容易有下面的动态规划方程的递推式：
$\beta (s_{k-1})={\sum }_{s_k}\psi (s_{k-1},s_k)\beta (s_k)$

那么，这样就有：
$\psi (\vec{x})=\beta (0)={\sum }_{s_1}\psi (\ast ,s_1)\beta (s_1)$

该动态规划方程的递推式便是前后向算法的backward阶段（后向阶段），其初始值定义为：
$\beta (s_n)=\psi (s_n,STOP)$

伪代码实现如下：

＃n为序列x的长度
for s in S:
    beta(n, s) = psi(s, STOP)##n表示第一轮，该轮的终点是stop(一种选择),起始是s（s种选择），s表示起点
for(m = n-1; m >= 1; m--):
    for s in S:
        for s' in S:
            beta(m, s) += psi(s, s') * beta(m+1, s')##m表示第m轮，该轮的终点是 s' （s种选择）,起始是 s（s种选择）,把起始的s种选择的结果相加后才是beta(m, s) 
for s in S:
    beta(0, *) = psi(*, s) * beta(1, s) ##0表示第0轮，该轮的终点是s (s种选择),起始是 *（1种选择）,把起始的s种选择的结果相加后才是beta(0, *) ，

说实话，以前对前向后向算法，总是似懂非懂的转态，看公式能连起来后，但公式的 前后由来，总是断的，这次一次性由头到尾地看前向后向算法，算是真看懂了。

之所以要通过 求前向后向算法中的 $\beta (m,s),\alpha (m,s)$。其实是为了求我们之前提到的$p(s_{k-1}=a,s_k=b|x)$这种边缘概率，或者说条件概率。

有上述的动态规划方程的前向后向算法，我们可以很方便求解$\alpha ,\beta$所对应的各个值。
下面推导如果用$\alpha ,\beta$，求出我们需要的条件概率。
对于$\alpha ,\beta$,现在我们考察发现：

$$\begin{gathered} \frac{\alpha (s_k)\beta (s_k)}{\psi (\vec{x})} \\ =[\sum _{s_{k-1}}\psi (s_{k-1},s_k)[\sum _{s_{k-2}}\psi (s_{k-2},s_1)...[\sum _{s_1}\psi (s_1,s_2)[\psi (\ast ,s_1)]]...]] \\ \ast \\ [\sum _{s_{k+1}}\psi (s_k,s_{k+1})...[\sum _{s_{n-1}}\psi (s_{n-2},s_{n-1})[\sum _{s_n}\psi (s_{n-1},s_n)[\psi (s_n,STOP)]]]...] \\ =\frac{{\sum }_{s_1}{\sum }_{s_2}...{\sum }_{s_{k-1}}{\sum }_{s_{k+1}}...{\sum }_{s_n}{\prod }_j\psi (s_{j-1},s_j)}{\psi (\vec{x})} \\ =p(s_k|\vec{x}) \end{gathered}$$

也就是说：
$p(s_k|\vec{x})=\frac{\alpha (s_k)\beta (s_k)}{\psi (\vec{x})}$

同理可得，
$p(s_k,s_k|\vec{x})=\frac{\alpha (s_{k-1})\psi (s_{k-1},s_k)\beta (s_k)}{\psi (\vec{x})}$

由于能高效求出$\alpha ,\beta$,边缘概率$p(s_k,s_k|\vec{x})、p(s_k|\vec{x})$也可高效求出，进而我们可以精确高效地求出梯度！
只要能快速求解梯度，接下来我们就可以利用SGD或者L-BFGS对CRF进行快速参数估计。

下面我们就继续讲如何从$\alpha ,\beta$,边缘概率$p(s_k,s_k|\vec{x})、p(s_k|\vec{x})$来得出CRF的求导式子，也即是源码中真正用于更新参数的式子。

这里我们就要又回到上一篇提到的损失函数（似然函数）式子了，

原始论文的阐述形式是CRF是一种概率图模型，而一幅图可以由它的边和节点来表达，也就是
G=(V,E)
其中，V是节点集合，E是边集合，对于链式CRF，模型对于输入序列和输出序列可以建立如下的概率模型：
$p(\vec{y}|\vec{x})=\frac{exp({\sum }_{e\in E}{\sum }_k{w}_k{\varphi }_k(e=(y_{i-1},y_i),\vec{x})+{\sum }_{v\in V}{\sum }_t{w}_t{\varphi }_t(v=y_i,\vec{x}))}{Z}$

这种形式和我们常见的另一种形式其实又很大区别，另一种形式是：

$p(\vec{y}|\vec{x})=\frac{exp({\sum }_i{\sum }_k{w}_k{\varphi }_k(y_{i-1},y_i,\vec{x}))}{{\sum }_{y^{{}^{\prime }}\in Y}exp({\sum }_i{\sum }_k{w}_k{\varphi }_k(y_{i-1}^{{}^{\prime }},y_i^{{}^{\prime }},\vec{x}))}$

下面的这种形式是没有将边和节点区分开来，看上去只是写了边的特征函数，因为从某种程度上看，边包含的信息其实已经涵盖了节点所拥有的所有信息，将这两者统一起来只是有利于我们数学公式表达的方便性，另一方面，将边和节点进行单独讨论，从理论上可能有一点冗余， 但从实际效果来讲以及实际源码编写中看，都是边和节点区分开来写源码的，节点信息可以充当一种backoff，起到一定的平滑效果(Smoothing)。

下面我们就看 CRF的似然函数或者损失函数的式子：

$L=-{\sum }_i^{N}logp({\vec{y}}^i|{\vec{x}}^i)$

带入$p(\vec{y}|\vec{x})=\frac{exp({\sum }_{e\in E}{\sum }_k{w}_k{\varphi }_k(e=(y_{i-1},y_i),\vec{x})+{\sum }_{v\in V}{\sum }_t{w}_t{\varphi }_t(v=y_i,\vec{x}))}{Z}$这个式子，我们对$w_j$进行求导，要分为两种，即分别是对图节点参数求导和对边参数求导。

$$\begin{gathered} \frac{\partial L}{\partial w_j}=\sum _i^N(\sum _{v\in V}p(v=y|\vec{x}){\varphi }_j(v,\vec{x})-\sum _{v\in V}{\varphi }_j(v,\vec{x})) \\ =\sum _i^N(E_{v\sim p(v|\vec{x})}{\varphi }_j(v,\vec{x})-\sum _{v\in V}{\varphi }_j(v,\vec{x})) \\ =\sum _i^N(\sum _{v\in V}\frac{\alpha (v)\beta (v)}{Z}-\sum _{v\in V}{\varphi }_j(v,\vec{x})) \end{gathered}$$

上面的式子第二步写出了一种期望的形式，这也就是为什么有些crf的博客里在参数求导时会提到期望的概念。
从第二步到第三步的过程中，我开始看了好几遍以为是 公式写错了，总是觉得少写了一项。因为
$\frac{\alpha (v)\beta (v)}{Z}$明明应该对应于$p(v=y|\vec{x})$， 怎么又对应于$p(v=y|\vec{x}){\varphi }_j(v,\vec{x})$ 呢？

后面忽然灵光一现，因为只看公式，没想到公式背后的含义，${\varphi }_j(v,\vec{x})$ 的物理含义是在i这个位置上，第j个特征函数 取到的特征函数值，由于特征函数的定义只取为0或1。 所以在这种特殊取值的情况下，推导的时候，会有${\sum }_{v\in V}\frac{\alpha (v)\beta (v)}{Z}={\sum }_{v\in V}\frac{\alpha (v)\beta (v)}{Z}{\varphi }_j(v,\vec{x})$成立。

同理对边参数求导如下：

$$\begin{gathered} \frac{\partial L}{\partial w_j}=\sum _i^N(\sum _{e\in E}p(e=(y_{i-1},y_i)|\vec{x}){\varphi }_j(e,\vec{x})-\sum _{e\in E}{\varphi }_j(e,\vec{x})) \\ =\sum _i^N(E_{e\sim p(e|\vec{x})}{\varphi }_j(e,\vec{x})-\sum _{e\in E}{\varphi }_j(e,\vec{x})) \\ =\sum _i^N(\sum _{e\in E}\frac{\alpha (y_{i-1})\psi (y_{i-1},y_i)\beta (y_i)}{Z}-\sum _{e\in E}{\varphi }_j(e,\vec{x})) \end{gathered}$$

这里的$\psi (y_{i-1},y_i)$,就是我们在前向后向公式推导中 引入的因子，即
$\psi (y_{j-1},y_j)=exp({\sum }_k{w}_k\varphi (y_{j-1},y_j,\vec{x}))$

$\varphi$是特征函数，节点特征函数一般由Unigram模板产生，边特征函数由Bigram模板自动产生，$\alpha ,\beta$的计算用上面我们介绍的forward-backward算法既可高效求解。

下篇，准备参照
https://blog.youkuaiyun.com/aws3217150/article/details/69212445
中提到的源码片段，对应介绍上面提到的对节点参数和边参数求导的公式。