首先是csdn上大佬的解释:将较大余数分块即107和17的最大公约数可以看作17+90和17的公约数。接下来将117和17的最大公约数设为m,那么17+90和17的公约数也为m,其中17和107都可以被m整除那么90也可以被m整除,那接下来就是计算90和17的最大公约数,然按照刚刚的方法继续求下去。
接下来我产生了一个疑问为什么剩下来的那部分也可以被整除就求出来,然后看了b站的大佬的公式解释:首先我们设a,b(a>b)两个数,设他们的最大公约数为t,接下来a和b的关系就可以写成a=nb+c,转换一下便是a/b=n....c,然后我们设a/t=x,b/t=y既a=xt,b=yt,将初始式子进行转化可以求得c=a-nb=xt-nyt=(x-ny)t,由此可知余数c也是最大公约数的倍数。
最后就是关于它的图文理解
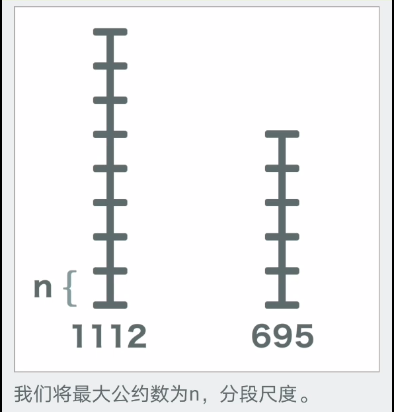
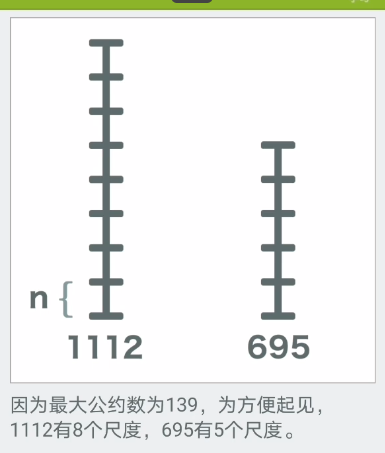
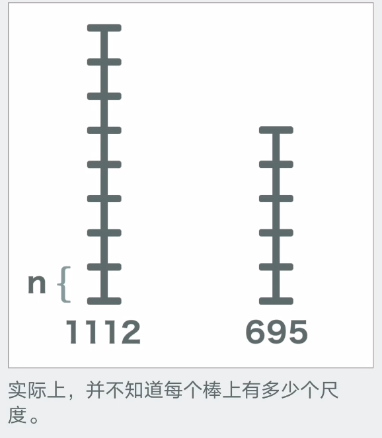
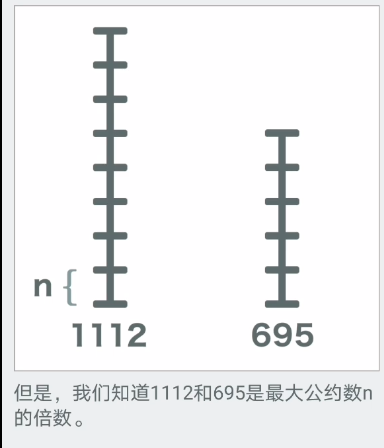
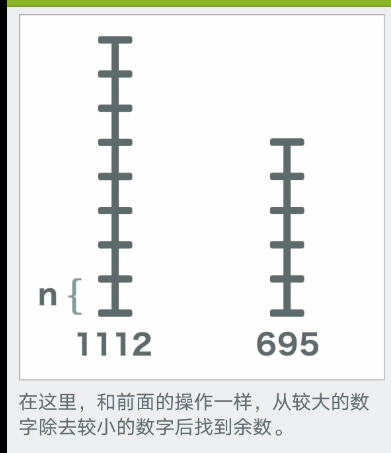

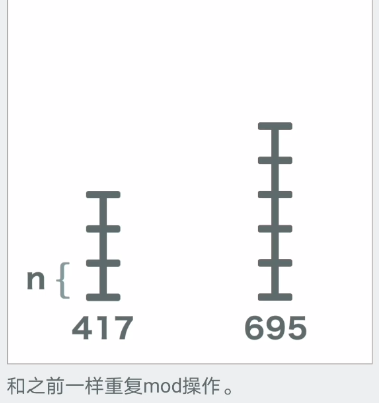








 文章探讨了如何使用分块方法和欧几里得算法来求解两个数的最大公约数。通过优快云和B站上的解释,阐述了当较大余数被分解后,其部分仍能被最大公约数整除的原理,并介绍了将数对关系转换为线性表达式的数学技巧,证明余数也是公约数的倍数。
文章探讨了如何使用分块方法和欧几里得算法来求解两个数的最大公约数。通过优快云和B站上的解释,阐述了当较大余数被分解后,其部分仍能被最大公约数整除的原理,并介绍了将数对关系转换为线性表达式的数学技巧,证明余数也是公约数的倍数。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








