CS336笔记2-Architectures,Hyperparameters

timeline：

11月4日-14日

Architectures

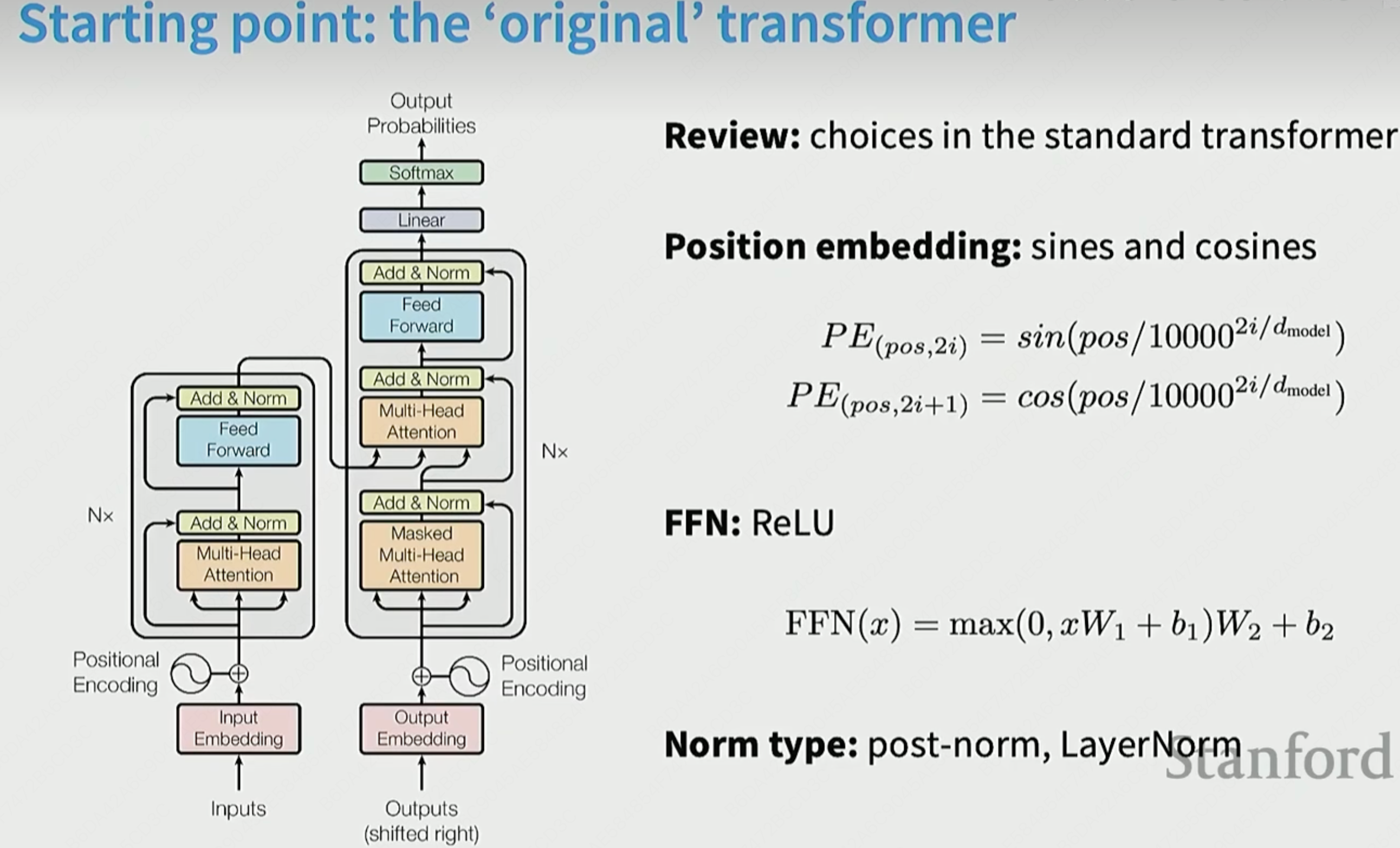
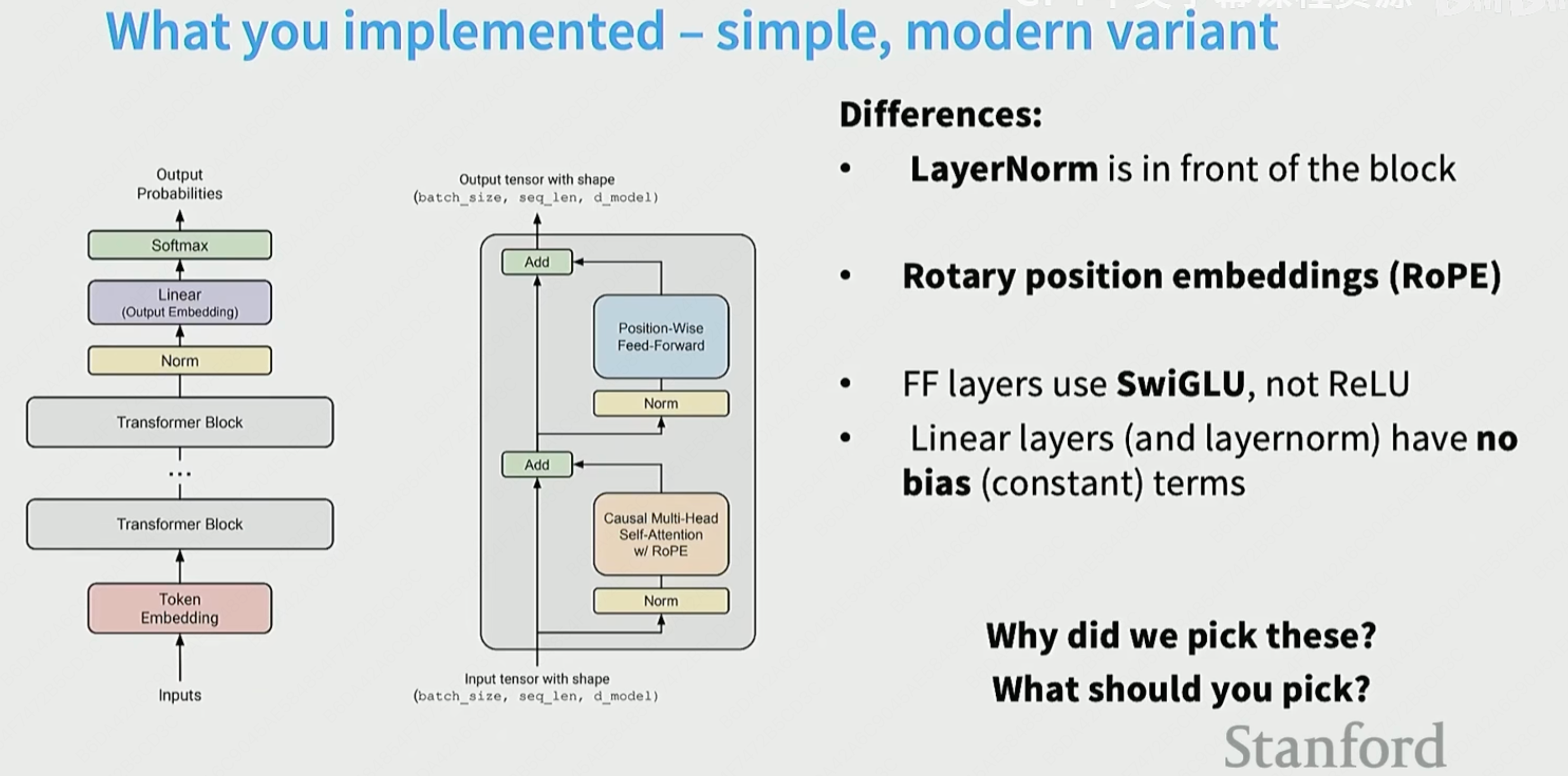
Postnorm vs Prenorm

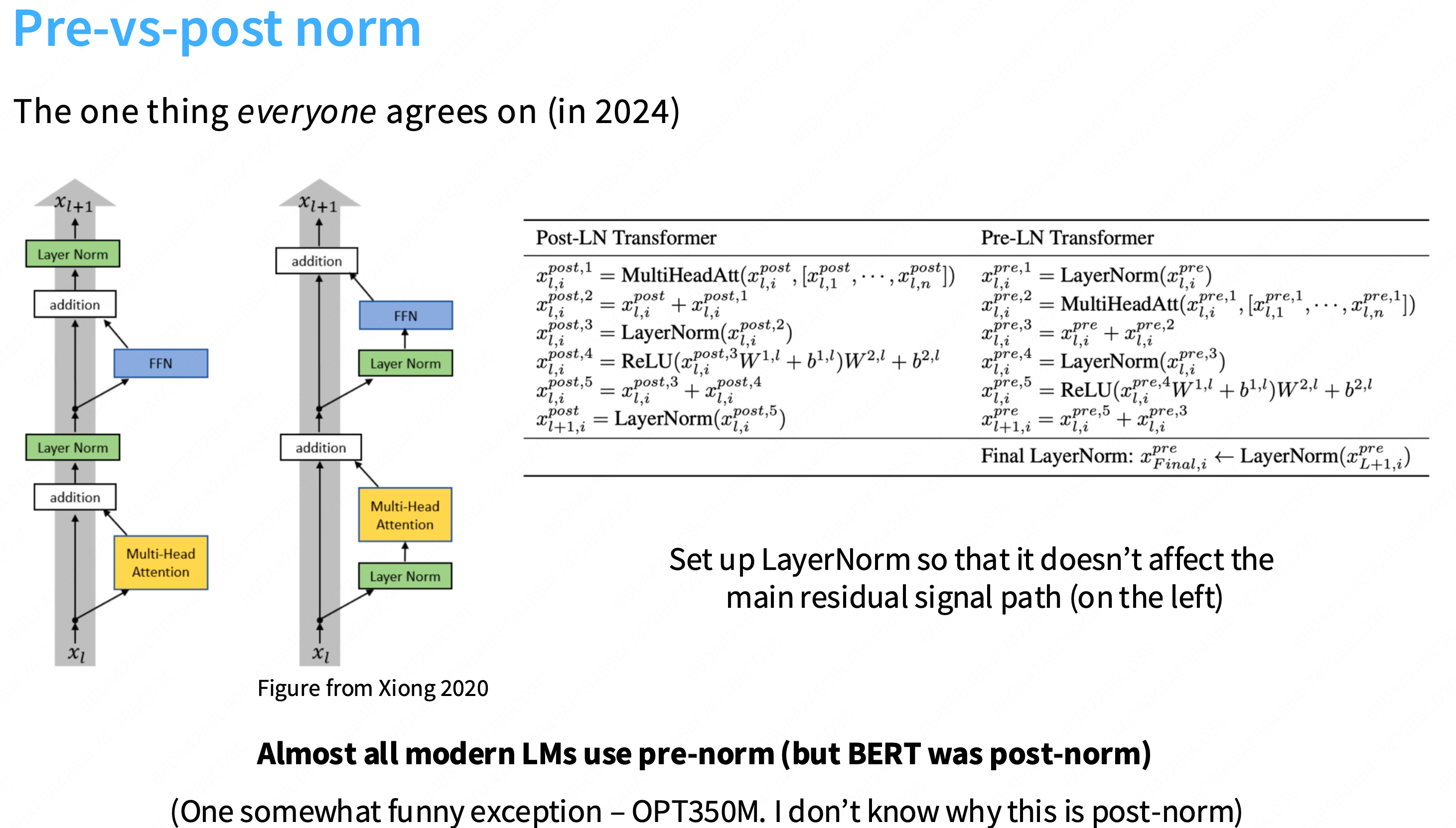
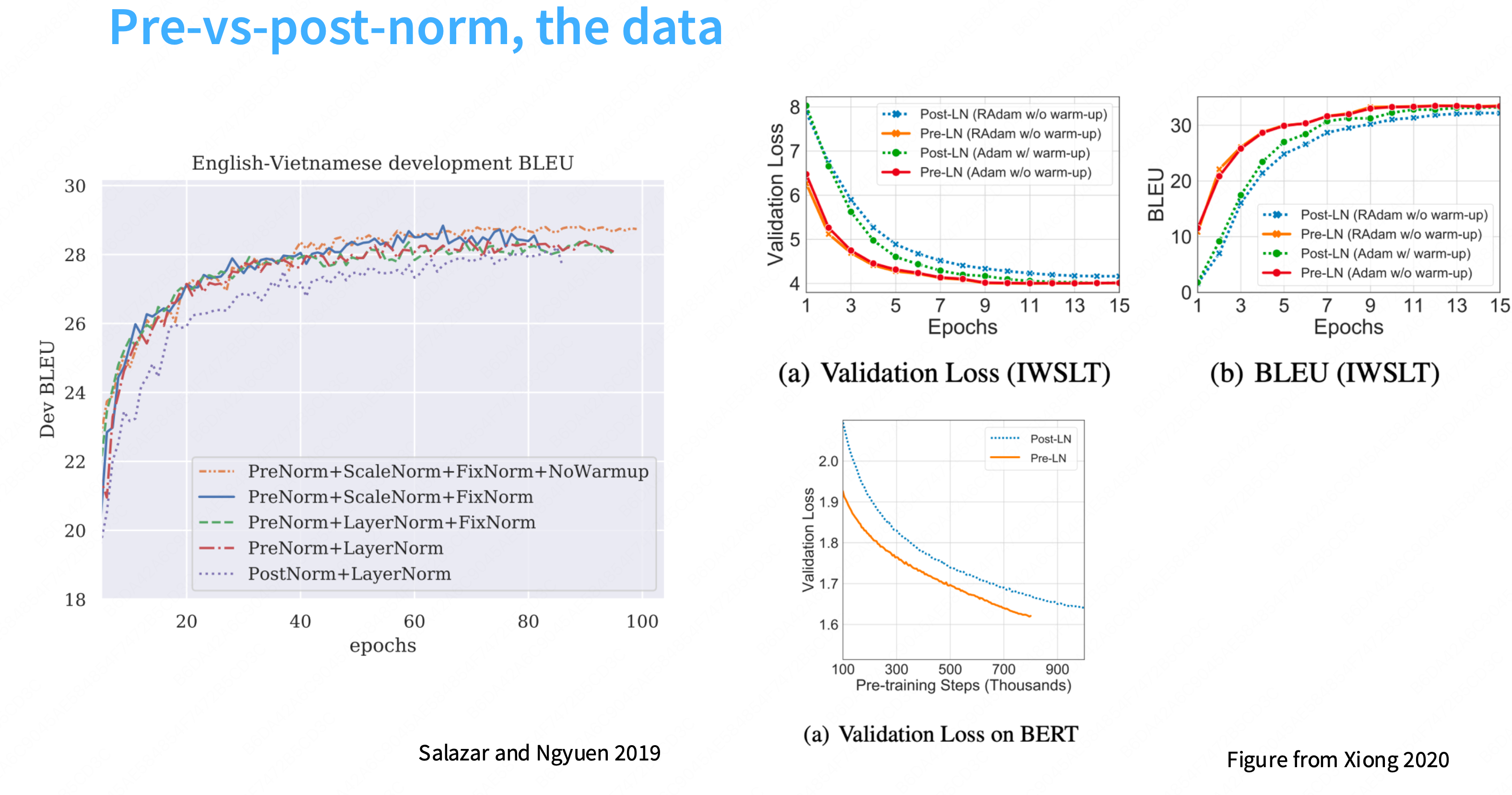
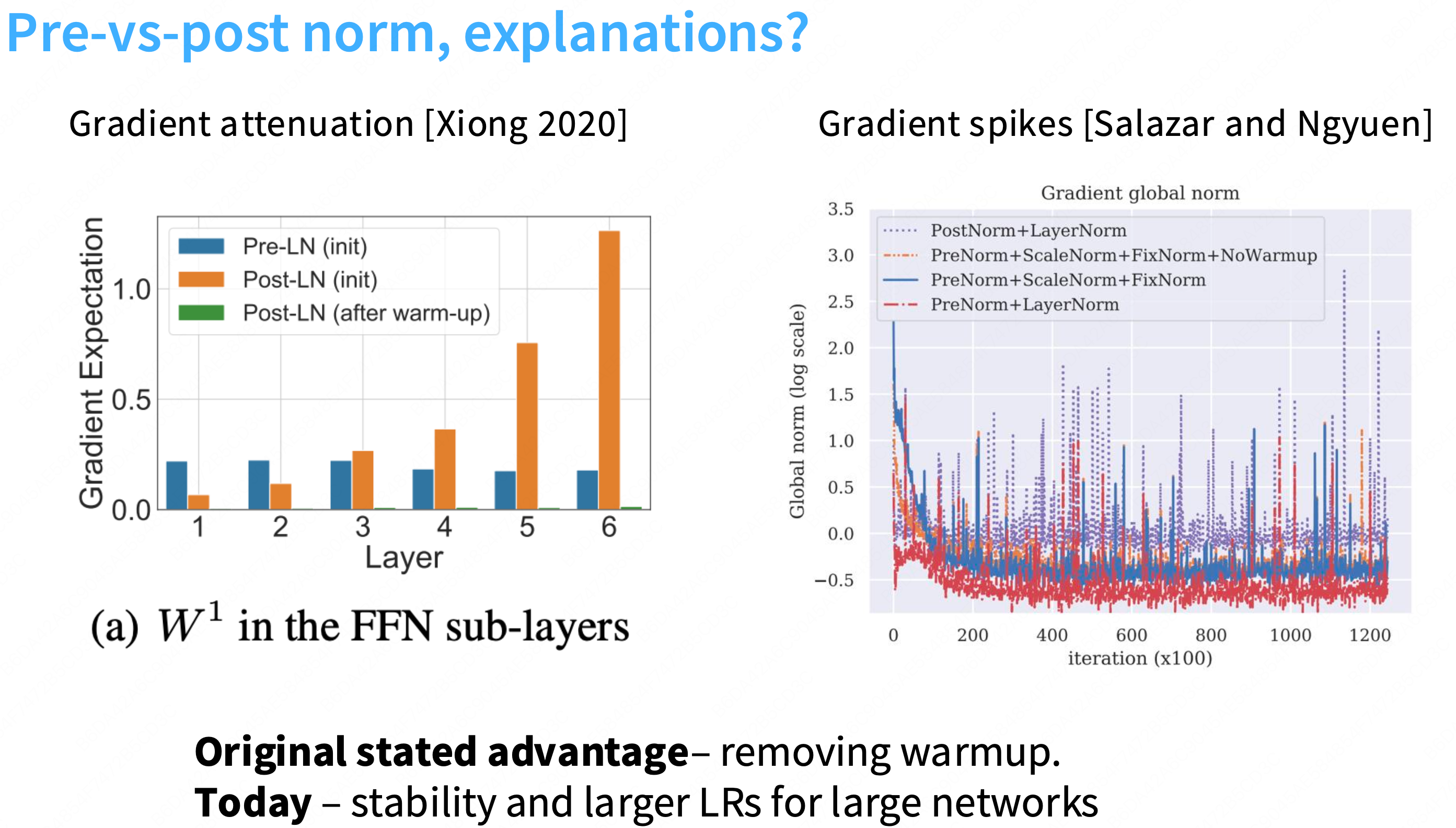
        为什么layernorm放在前面更加有效？

        更多的一种解释是：“前置归一化是一个更加稳定的训练架构”。不容易出现梯度尖刺的情况，更加稳定。在残差流中放置layernorm是不好的 

        Q: 为什么在残差流中加入layernorm不好？

        a: 一个直观的观点是，残差给你从网络顶部到底部的这种恒等链接，因此，如果你视图训练非常深的网络，这使得梯度传播非常容易，因此，有很多关于lstm和其他状态空间模型在反向传播梯度时困难的讨论，但这种恒等链接没有任何这样的问题，因此，在中间放置layernorm可能会干扰这种梯度行为。

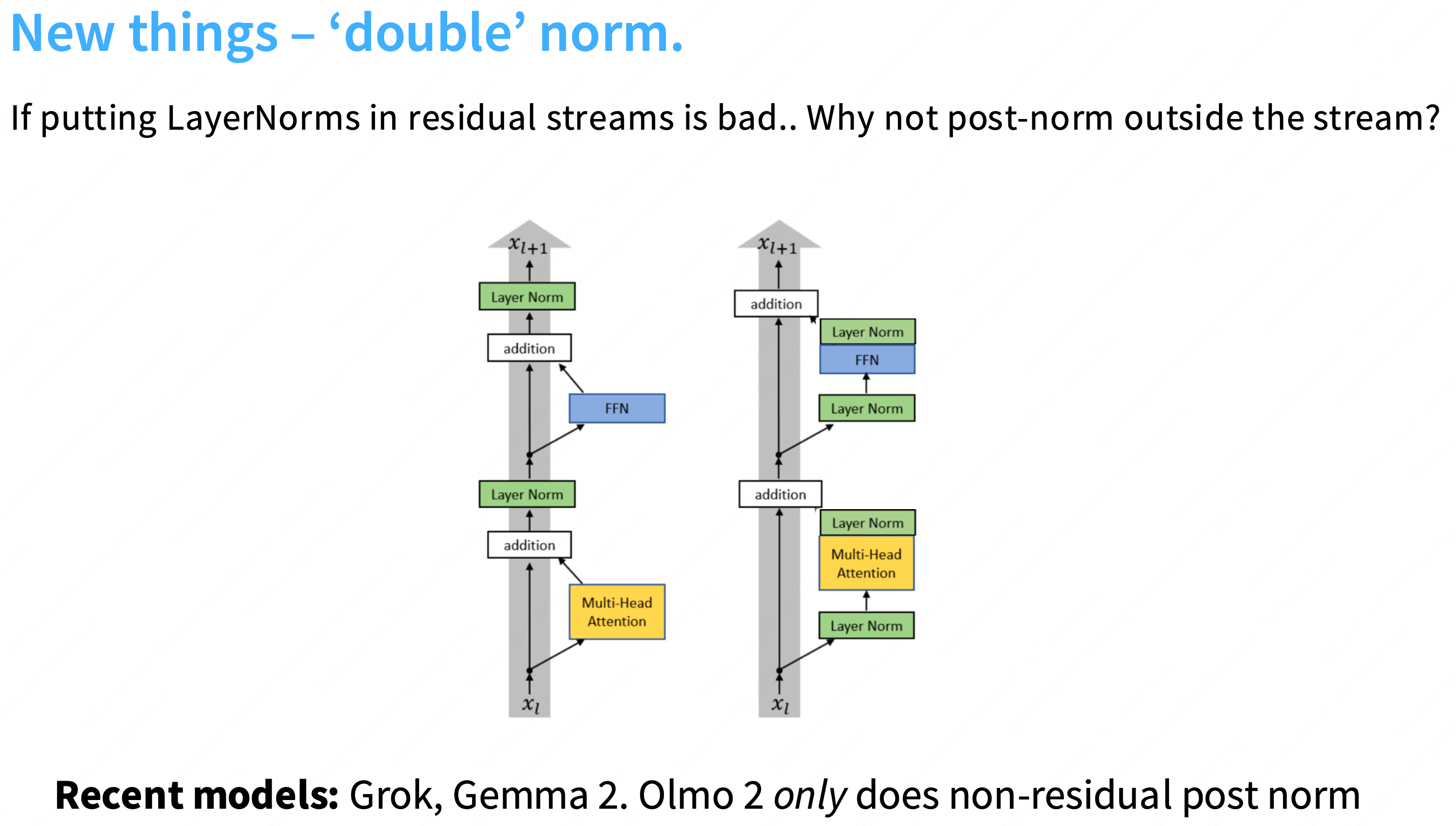
LayerNorm vs RMSNorm

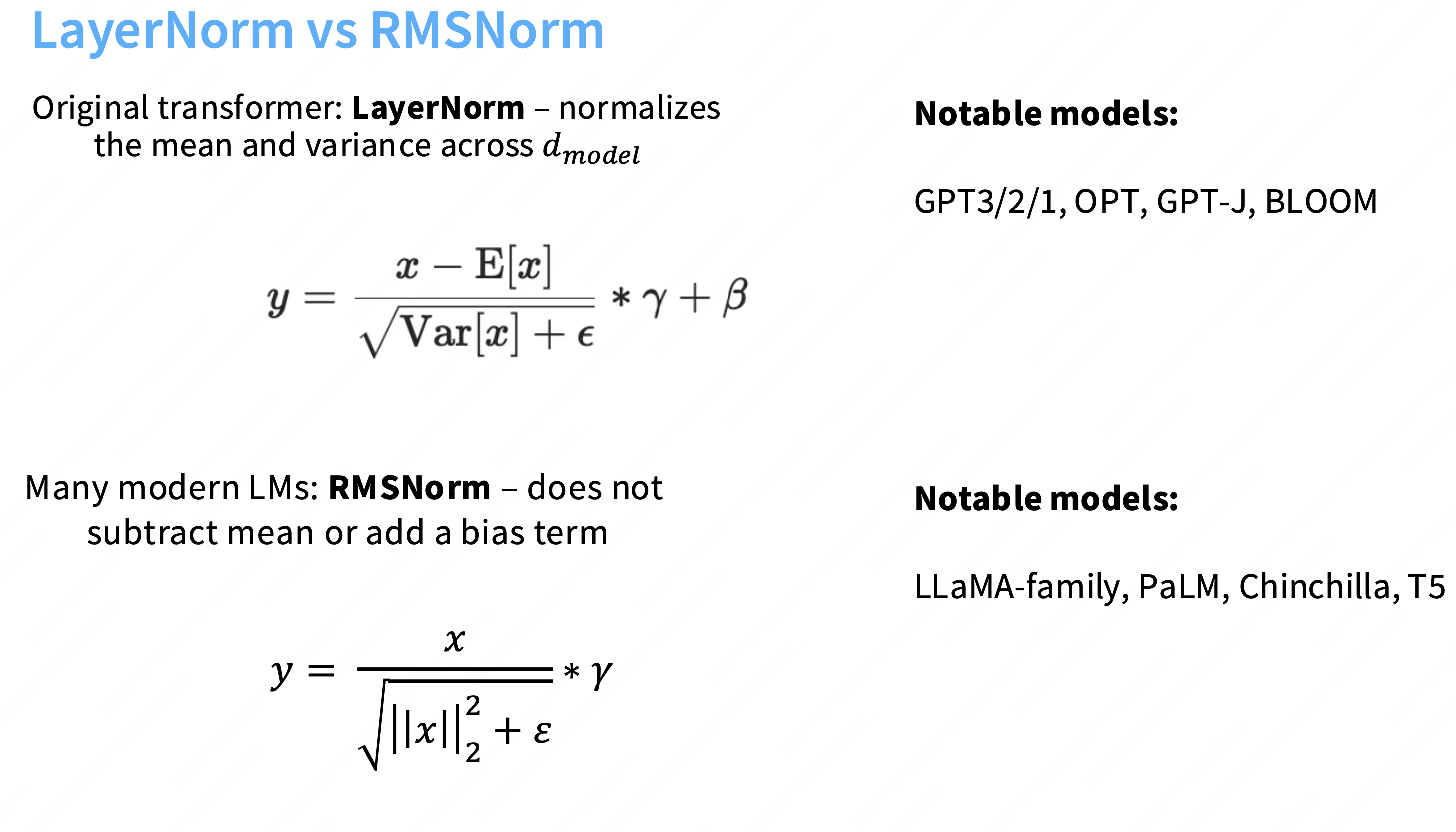
可以简单的认为layernorm就是一个标准差，然后通过一个gamma因子γ放大。

Q：为什么当前的模型都转向于使用rmsnorm？

A：因为使用RMSnorm和使用layernorm效果一样好，现代模型（尤其是 LLaMA 系列）偏向于使用 RMSNorm 的最主要、最直接的原因是：为了提高计算效率（即速度）。

①不需要再减去均值，不必添加bias，需要从内存加载回计算单元的参数就会变少。

②虽然RMSnorm优化的浮点计算量仅在transformer中占比0.17%，但这并不是唯一需要考虑的。因为计算量flops≠运行时间runtime。还需要仔细的考虑内存移动。

        下图可以看到，虽然归一化（如layernorm、softmax等）所占的计算量仅有0.17%，但是实际运行时间占比达到了25%。一个核心原因是:归一化操作仍然会产生大量的内存移动开销，因此优化这些底层的操作十分重要。

右边这张图有点意思，不仅仅是一个架构图（它展示了 MHA 子层），更是一个性能瓶颈分析图。

核心概念：两大瓶颈

GPU 只有两种工作状态，这由计算强度 (AI) 决定：

1. 计算受限 (Compute-Bound)

   • 高 AI (如 153)

   • 含义： 每从显存 (HBM) 中读取 1 字节的数据，GPU 都能执行大量的计算（例如 153 次 FLOPs）。

   • 状态： GPU 的计算核心（Tensor Cores）100% 繁忙，而显存正在“休息”。这是理想状态，能实现高 MFU。

2. 内存带宽受限 (Memory-Bound)

   • 低 AI (如 3.5 或 1/3)

   • 含义： 每读取 1 字节，GPU 只能执行很少的计算。

   • 状态： GPU 的计算核心极其空闲（“挨饿”），大部分时间都在“等待”数据从缓慢的 HBM 显存加载到高速的 SRAM 缓存中。这导致 MFU 极低。

3. 逐一分析图中组件：现在，我们用这个“瓶颈”视角来分析这张图：

a) MHA (Multi-Head Attention)

• FLOPs (43G): 430 亿次运算。这几乎是这个块的全部计算量 (43G vs 4M+4M+29M)。

• AI (153): 极高！结论： MHA 是**“计算受限 (Compute-Bound)”**的。

• CS336 关联： 这完全符合我们的推导。MHA 的核心是 Q@K.T 和 scores@V 这样的大型矩阵乘法 (Matmul)，它们具有极高的计算强度。这部分是“好”的，能跑满 MFU。

b) Dropout 和 + (残差连接)

• FLOPs (4M): 仅 400 万次运算，计算量完全可以忽略不计。

• AI (1/3): 极低！ (小于 1)

• 结论： 它们是**“内存带宽受限 (Memory-Bound)”**的。

• CS336 关联： 这也符合我们的推导。Dropout 和 Add 都是逐元素 (Element-wise) 操作（图例 ○）。它们需要从 HBM 读取整个 [B, L, D] 张量，只做 1 次乘法或加法，再写回 HBM。这是纯粹的 I/O 瓶颈。

c) LayerNorm

• FLOPs (29M): 计算量也基本可以忽略不计。

• AI (3.5): 非常低！

• 结论： LayerNorm 是**“内存带宽受限 (Memory-Bound)”**的。

这张图用数据可视化了 CS336 中一个的核心性能问题：

1. 一个 Transformer 块 99% 以上的**计算量（FLOPs）**都集中在 MHA 和 FFN（图中未显示）中。

2. 但是，MHA 和 FFN 并不是唯一的性能瓶颈。

3. 诸如 LayerNorm, Dropout, Residual Add 这样的“辅助”操作，虽然计算量（FLOPs）小到可以忽略，但它们是**严重的“内存带宽受限”**操作。

4. 总的执行时间 = Time(Compute-Bound) + Time(Memory-Bound)。

5. 如果我们的 MFU 很低，很可能不是因为 MHA (43G FLOPs) 运行得慢，而是因为 GPU 的计算核心在空转，等待 LayerNorm (29M FLOPs) 慢悠悠地从 HBM 读写数据。

这精确地解释了为什么我们要痴迷于Kernel Fusion（内核融合），以及为什么 RMSNorm（比 LayerNorm 更快）会成为 LLaMA 的首选。

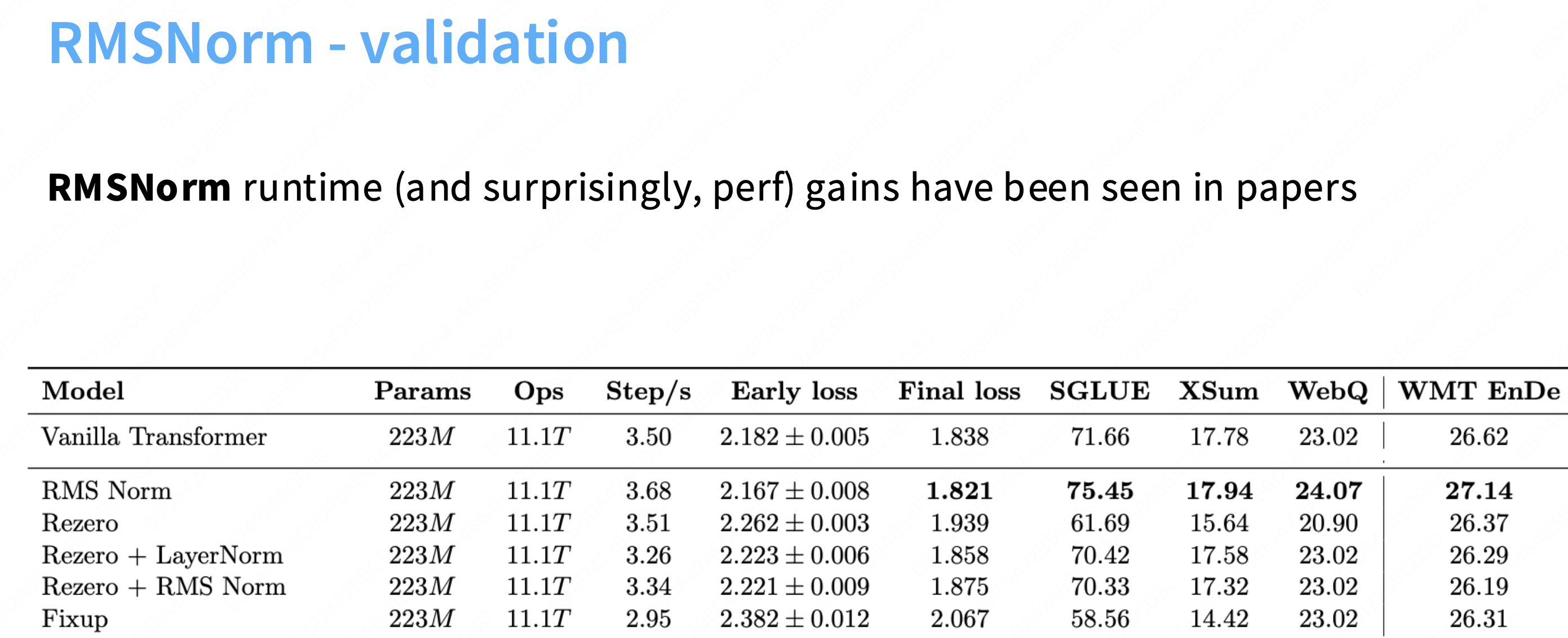
使用rmsnorm之后，step/s增加，final_loss也得到了优化。

去掉bias项

        经验上，去掉这些bias通常会稳定这些llm的训练。

layernorm总结

Activations

Gelu可以看到在x=0的附近有一个平滑的凹陷，具有可微性。φx是高斯累积分布函数 CDF。

• 平滑性： 它的曲线处处可导，这被认为能产生更平滑的损失“地形”（Loss Landscape），使优化器（Adam）更容易找到好的解，从而提升训练稳定性和最终性能。

• 非单调： 它在负值区域有轻微的“下凹”，允许（并惩罚）负值信息通过，这被认为比 ReLU 的“一刀切”更具表现力。

• 缺点： 计算上比 ReLU 昂贵得多（需要计算高斯 CDF）。

上面的幻灯片展示了（Reglu=relu+glu）的计算流程。

• 标准 FFN (Standard FFN): FF(x) = max(0, xW_1) W_2

  • 流程： x 经过一个线性变换 W_1，通过 ReLU 激活，再通过第二个线性变换 W_2。

• 门控 FFN (Gated FFN): FF_ReGLU(x) = (max(0, xW_1) ⊗ xV) W_2

  • 流程：

    1. x 同时经过两个并行的线性变换：W_1 和 V。

    2. xW_1 的结果通过 ReLU 激活。

    3. xV 的结果不经过激活（它是一个纯粹的线性项）。

    4. “门控 (Gating)”：将前两步的结果进行逐元素乘法 (⊗)。这个乘法就是“门 (Gate)”。它允许网络动态地、有选择地控制哪些信息可以流向下一层（类似于 LSTM 中的门控），这被证明比 GeLU 的静态激活要强大得多。

    5. 这个被“门控”后的结果，最后通过第三个线性变换 W_2。

GeGLU就是在ReGLU的基础上，将Relu换成Gelu。SwiGLU就是换成swish+glu。

        尽管 SwiGLU FFN（LLaMA 架构）与 GeLU FFN（GPT-3 架构）在总参数量 P 和总 FLOPs 上被设计为完全相同，但 SwiGLU 的实际训练速度更慢。为什么 FLOPs 相同，但速度（time_per_step）更慢？因为 FLOPs（理论计算量）不等于速度（实际硬件效率 MFU）。SwiGLU 的硬件效率更低，主要源于三个开销：

1. 内核启动开销 (Kernel Launch Overhead):

   • SwiGLU (3 Matmul + 2 逐元素操作) 需要启动 5 个 GPU 内核。

   • GeLU (2 Matmul + 1 逐元素操作) 只需要启动 3 个。

   • 更多的内核启动 = 更多的固定开销 = 更慢的速度。

2. 内存带宽瓶颈 (Memory-Bound):

   SwiGLU 增加了一个额外的逐元素乘法 (...) ⊗ (...)。这是一个纯粹的内存带宽受限操作。GPU 计算核心在执行此操作时“空转”等待数据，拉低了 MFU。

3. 计算强度 (AI) 效率:

   GPU Tensor Cores 执行 2 次“胖”的 Matmul (如 [D, 4D]) 的效率（MFU）高于执行 3 次“瘦”的 Matmul (如 [D, 2.67D])。SwiGLU 的“瘦” Matmul 导致硬件利用率下降。

        最终的权衡 (Trade-off)： LLaMA 的设计者故意做出了这个权衡：他们接受了较慢的训练速度（time_per_step 稍高），以换取在相同参数预算（P）下更优异的模型质量（更低的 Loss）。

总结：

Serial vs Parallel layers

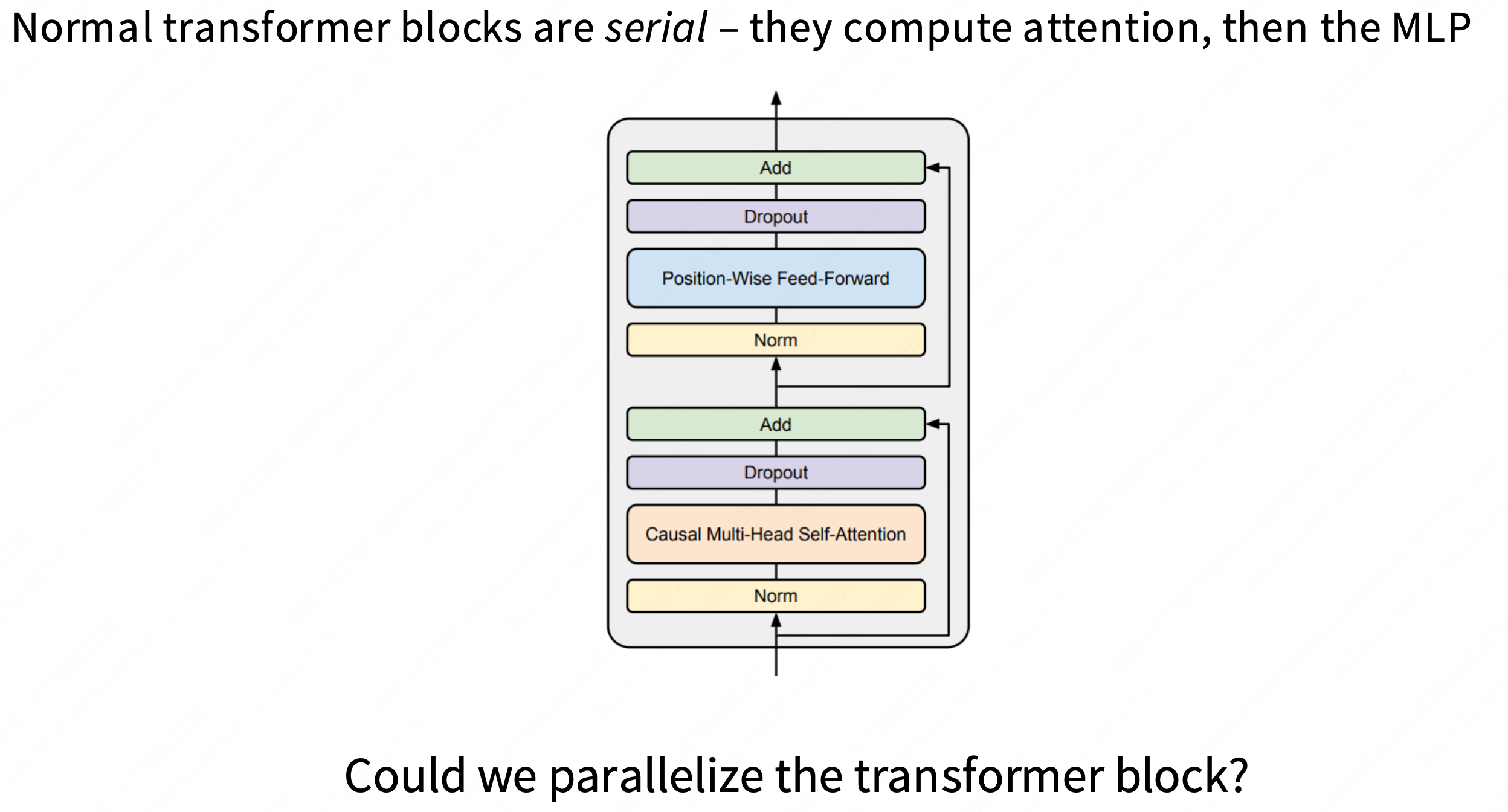
• 标准串行 (Serialized) 架构 (GPT-2 风格):

  • y = x + Attention(LayerNorm(x)) (MHA 块)

  • z = y + MLP(LayerNorm(y)) (FFN 块)

• 数据流： x 必须先完成 MHA 块的所有计算（Attention），得到 y 之后，才能开始 FFN 块的计算（MLP）。

• 瓶颈： MLP 必须等待 Attention，两者是串行的。

---

• 并行 (Parallel) 架构 (GPT-J / Cohere 风格):

  • y = x + MLP(LayerNorm(x)) + Attention(LayerNorm(x))

• 数据流：

  1. 对同一个输入 x 只进行一次 LayerNorm。（这是“if implemented right, LayerNorm can be shared”的含义）。

  2. LN(x) 的结果被同时喂给 Attention 块和 MLP 块。

  3. Attention(...) 和 MLP(...) 可以并行计算。

  4. 最后，将这两个块的输出与原始残差 x 一次性相加。

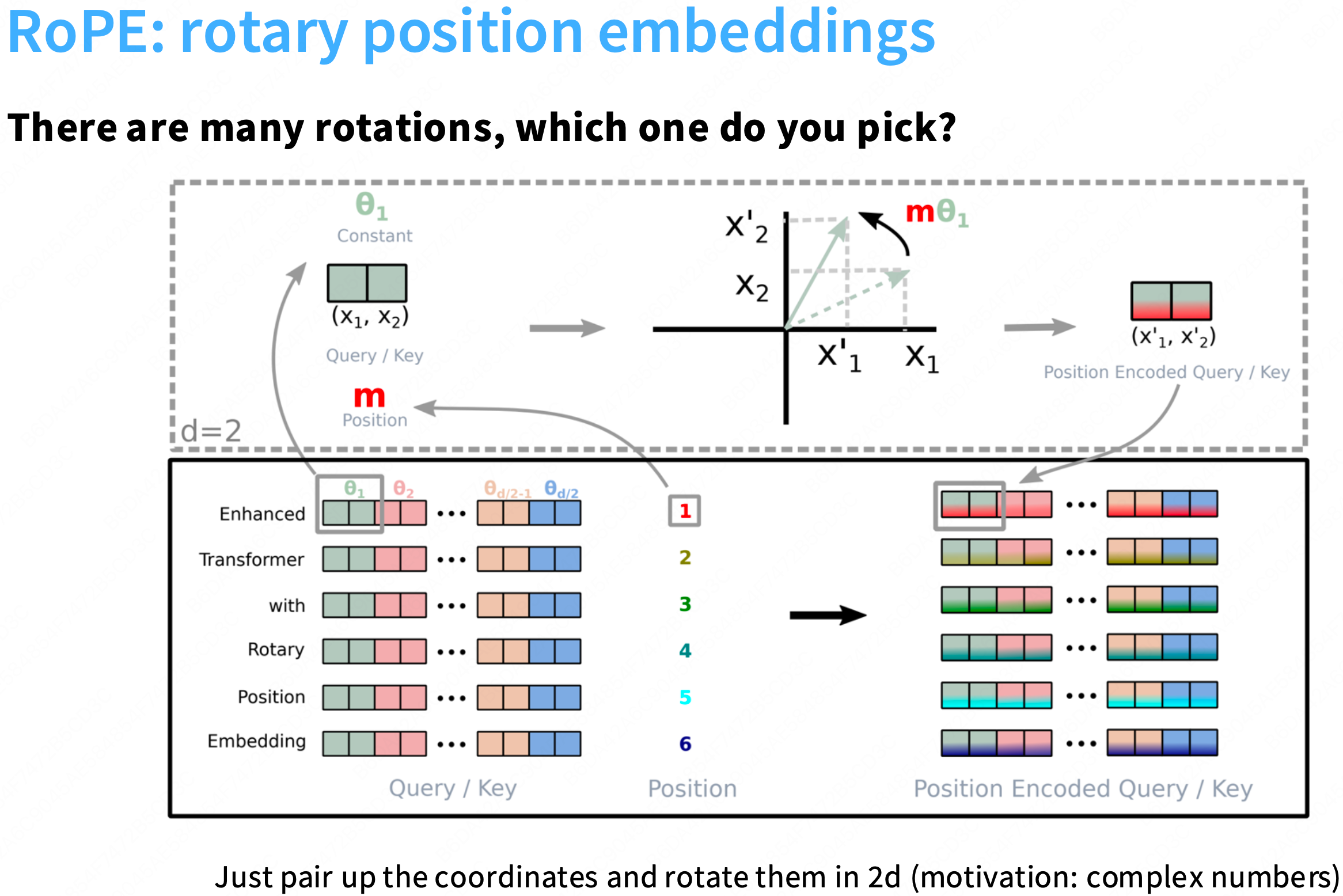
Position embeddings

        ROPE的高层思想：重要的是这些向量的相对位置。f(x,i)中的x是我要embedding的词，i是我的位置，你只关注词x和词y的距离。

        “RoPE 的设计哲学”：它首先定义了一个“完美”的相对位置编码应该满足的“黄金标准”，然后论证了为什么之前的所有方法（Absolute, Sine, T5-style）都不满足这个标准。

这张幻灯片接着“批判”了为什么所有老方法都不满足这个“黄金标准”：

思考：为什么这边一定要是inner product的形式？

        严格来说，它不必非要满足（T5 风格的相对偏置就不满足，也取得了成功）。

        但是，RoPE 的作者（以及 LLaMA, PaLM 的作者）之所以“执着”于将其保留为纯粹的内积（Inner Product / Dot Product）形式，是出于一个极其重要且具有前瞻性的架构设计考量：为了保持注意力计算的“纯粹性”，以实现极致的“硬件和算法兼容性”。

        我们来对比一下“T5 风格”和“RoPE 风格”的优劣：

1. “T5 风格”的缺陷（score = QK^T + bias）

• 形式： Attention(Q, K) = (Q @ K.T) + \text{relative_bias}

• 问题： 这不再是一个“纯粹的”点积。它是一个点积（Matmul）再加上一个逐元素相加（Element-wise Add）的操作。这在 CS336 的实践中会带来两个严重的性能问题：

1. 破坏了硬件优化（如 FlashAttention）：

   • 像 FlashAttention 这样的 SOTA（State-of-the-Art）优化技术，是专门为 softmax(Q @ K.T) 这个“端到端”的操作设计的“融合内核”（Fused Kernel）。它可以利用 GPU 的 SRAM 一次性完成计算，而无需将巨大的 (Q @ K.T) 矩阵（形状为 [B, H, L, L]）写回到缓慢的 HBM（显存）中。

   • 如果您使用 T5 风格，FlashAttention 就无法使用了。您必须：

     1. 计算 score = Q @ K.T (一次内核调用，结果写回 HBM)。

     2. 再启动一个全新的内核，从 HBM 读回 score，执行 score = score + bias (一次内存带宽受限的内核调用)。

   • 这个过程极其缓慢，彻底抵消了 FlashAttention 带来的所有速度优势。

2. 破坏了算法兼容性（如线性注意力）：

   • 许多高效的 Transformer 变体（如 Linear Transformers, Performers）依赖于**核方法（Kernel Methods）**来重排（re-arrange）计算顺序，例如将 softmax(Q K^T) V 替换为 Q (K^T V)，从而将计算复杂度从 O(L^2) 降到 O(L)。

   • + bias 这一项的加入，从数学上彻底破坏了这种重排的可能性。

   • 这意味着 T5 风格的位置编码无法与这些 $O(L)$ 的高效注意力算法兼容。

2. RoPE 的优越性 (score = Q'K'^T)

• 形式：

  1. Q' = f(Q, i) (在 MHA 之外，提前旋转 Q)

  2. K' = f(K, j) (在 MHA 之外，提前旋转 K)

  3. Attention(Q', K') = Q' @ K'.T

• 好处：

  • 注意力公式保持了“纯粹的点积”形式！

  • FlashAttention 完全不在乎你喂给它的是 Q 还是 Q'。它看到 Q' @ K'.T，就会立刻应用其融合内核进行超高速计算。

  • 所有的“线性注意力”算法也完全兼容。它们只需要对 Q' 和 K' 应用核函数即可。

总结：

        RoPE 的作者坚持“必须满足内积”形式，是一个极其聪明的工程决策。

        它确保了 RoPE 只是一个“即插即用”（Drop-in）的模块，它不会以任何方式“污染”或“破坏”下游的注意力计算公式。这使得 RoPE 完全兼容 FlashAttention 和各种线性注意力等所有旨在优化标准点积的 SOTA 技术，从而实现了极致的性能和未来的可扩展性。

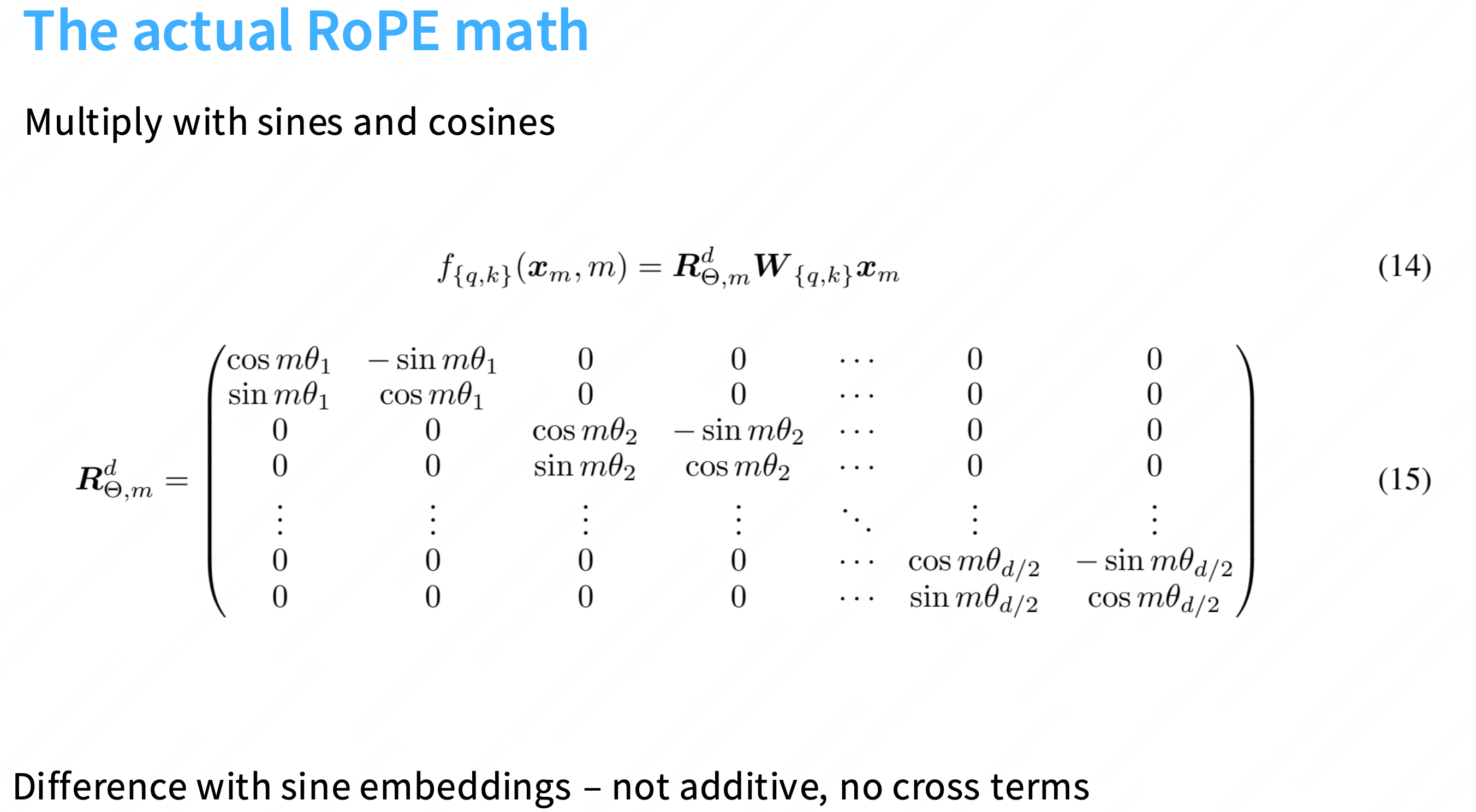
        内积只会关注距离的差异， 通常这种旋转在2d是非常明显的，但在高纬中不太明显。rope的做法是将高纬度D切分成二维的块， 每两个维度将被某个theta旋转，因此会有一个旋转速度，我们将旋转这些维度对。

        此时，每对维度都在编码所有这些的相对位置，就像在sin和cos 的embedding ，使得一些嵌入旋转得很快，而其他的嵌入旋转的更慢。因此，他们可以捕获高/低频信息or近距离、远距离的信息。

        可以将其视为嵌入向量 与 这些2*2块矩阵相乘的操作。这里面不涉及加法or交叉项，完美符合上面提出的原则->一切都是相对的。

        注意rope将在实际的注意力层进行操作， 而不是在底部添加位置编码。 只有当生成Query和Key的时候，需要这么计算拿到相对的位置信息。

Hyperparameters

feedforward size

        通常dff升维的维度是d_model的4倍（经验上）。下面是一些变体：

        这个是前面讲到的，glu为了保证总体的模型参数量不变，通常dff是d_model的8/3倍。

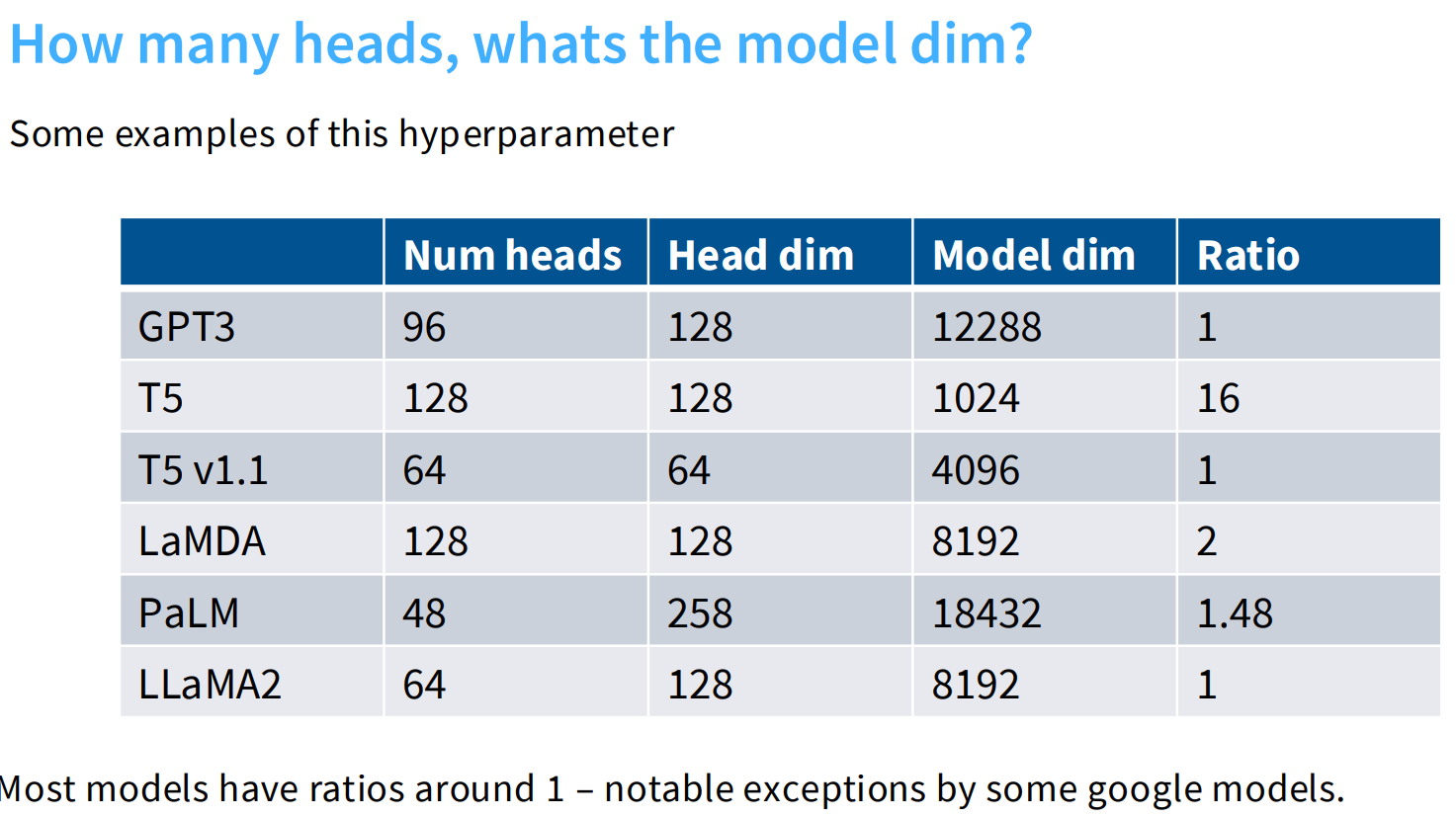
head-dim * num-heads 和model-dim的比例关系

        大部分head-dim * num-heads ≈ model-dim。

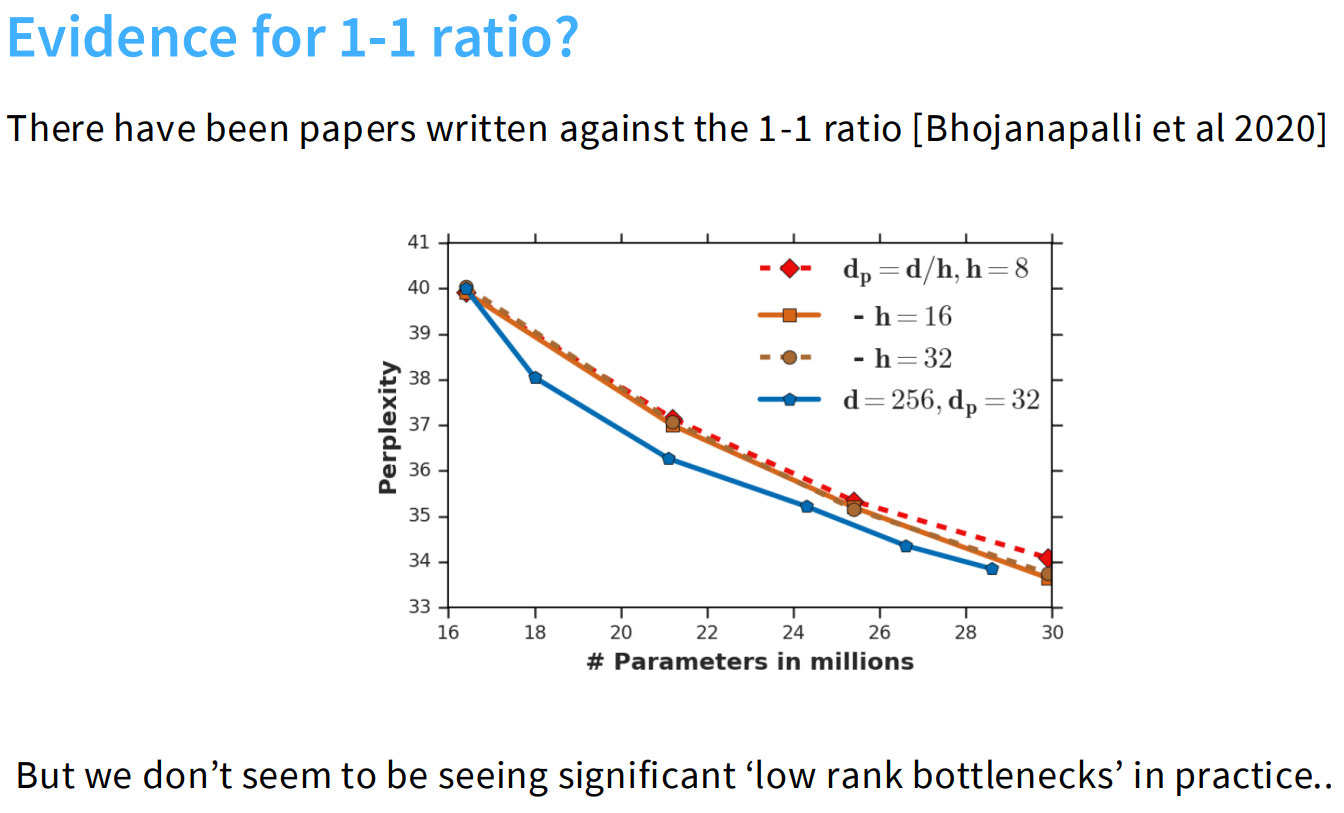
        bhoj等人提出，如果在ratio=1的情况下，num-heads越多，head-dim越小，维度小对应矩阵的rank越小，每个头的注意力表达能力有限--->但实际并没有太大的影响。

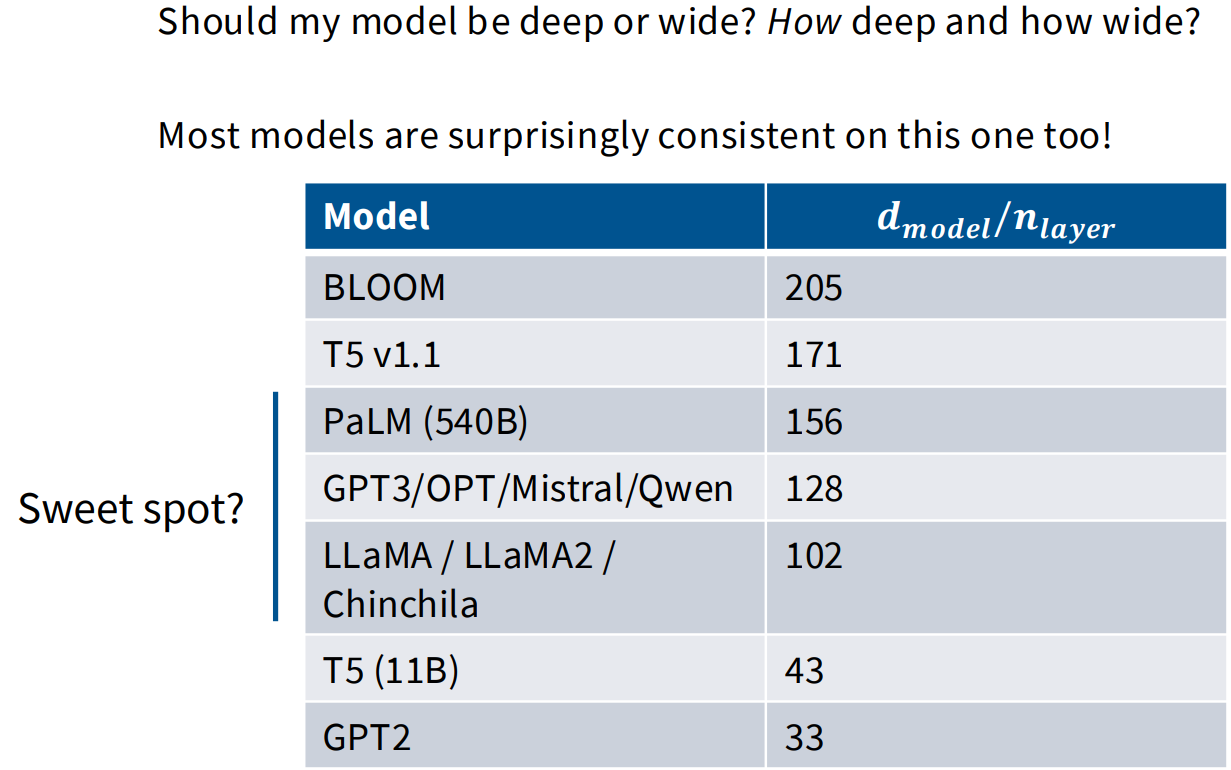
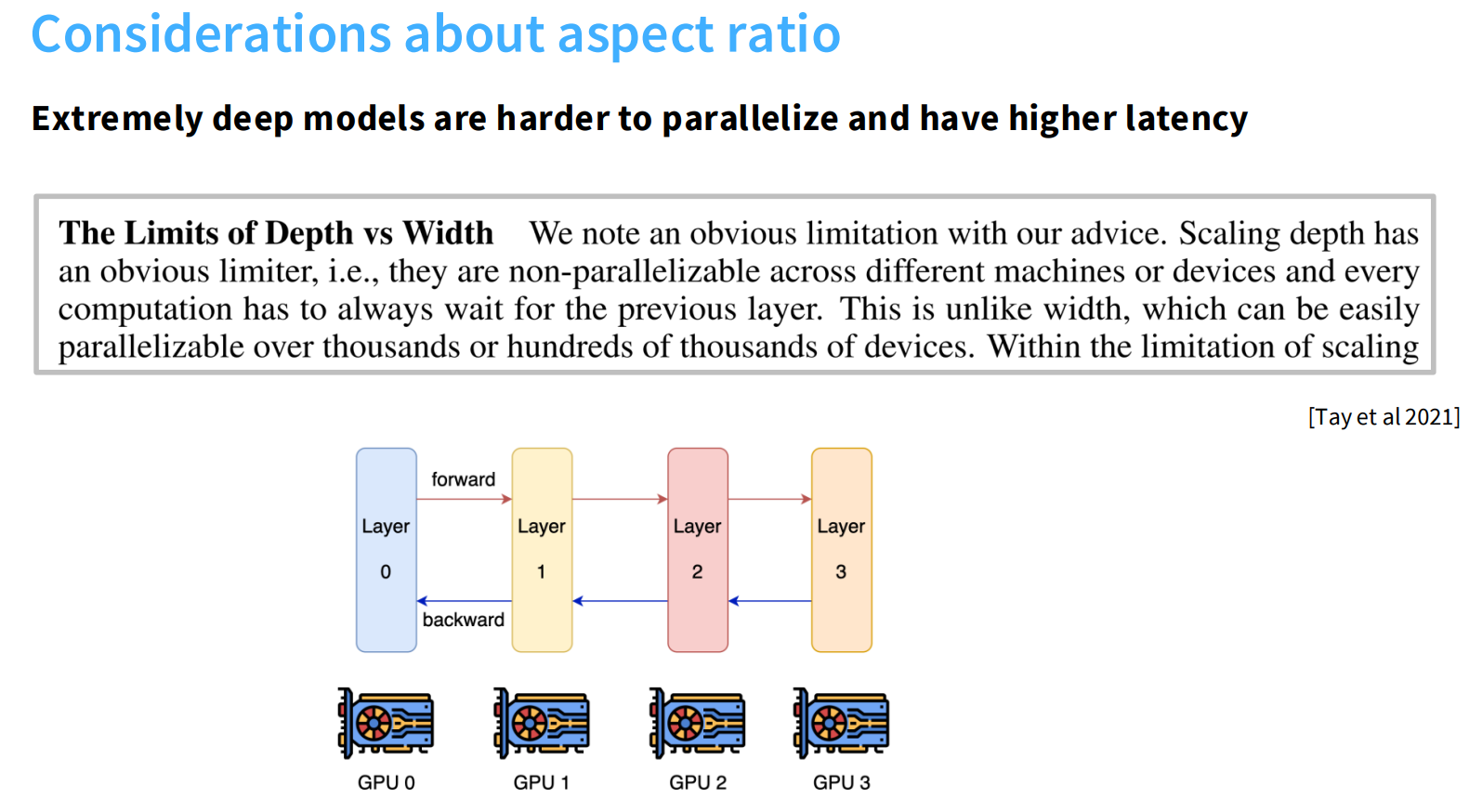
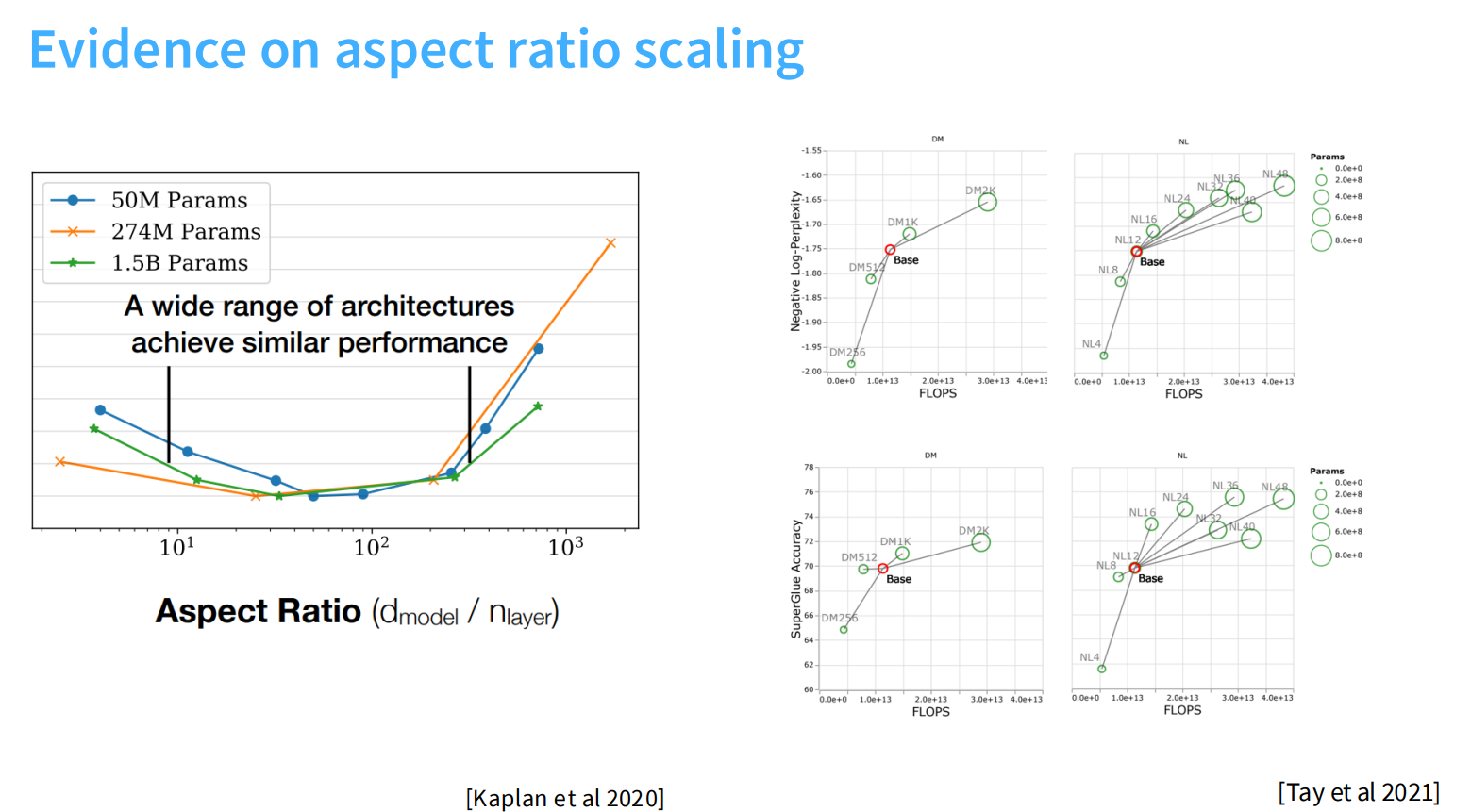
Aspect ratios 宽深比

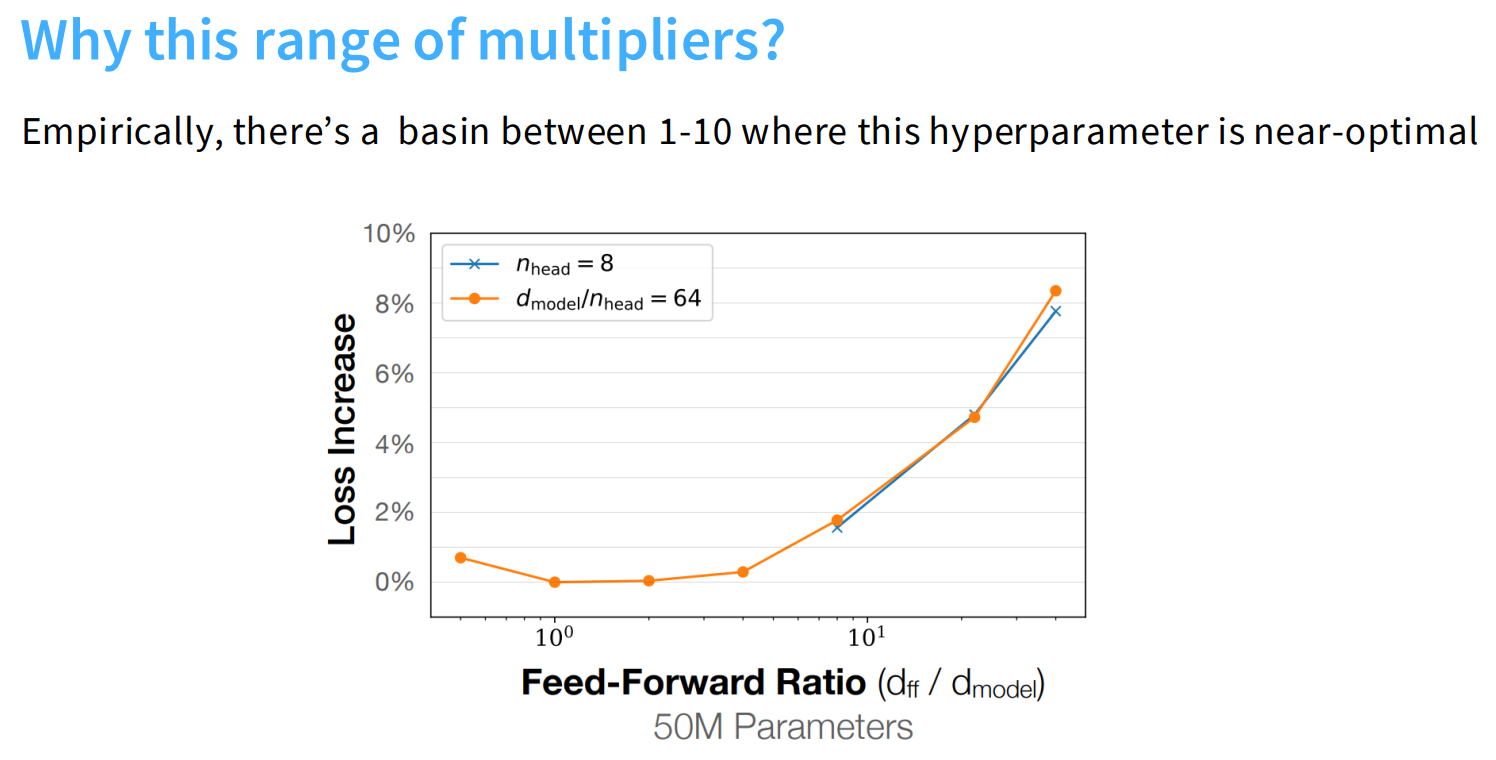
        通常来说，深度代表着模型更加聪明，宽度代表着计算的高效。Aspect ratios可以控制我们计算的并行化程度。

差不多在100左右区间，都能够达到不错的效果。现有的一些实验表明，aspect ratio大概会对下游任务会有较大的影响。

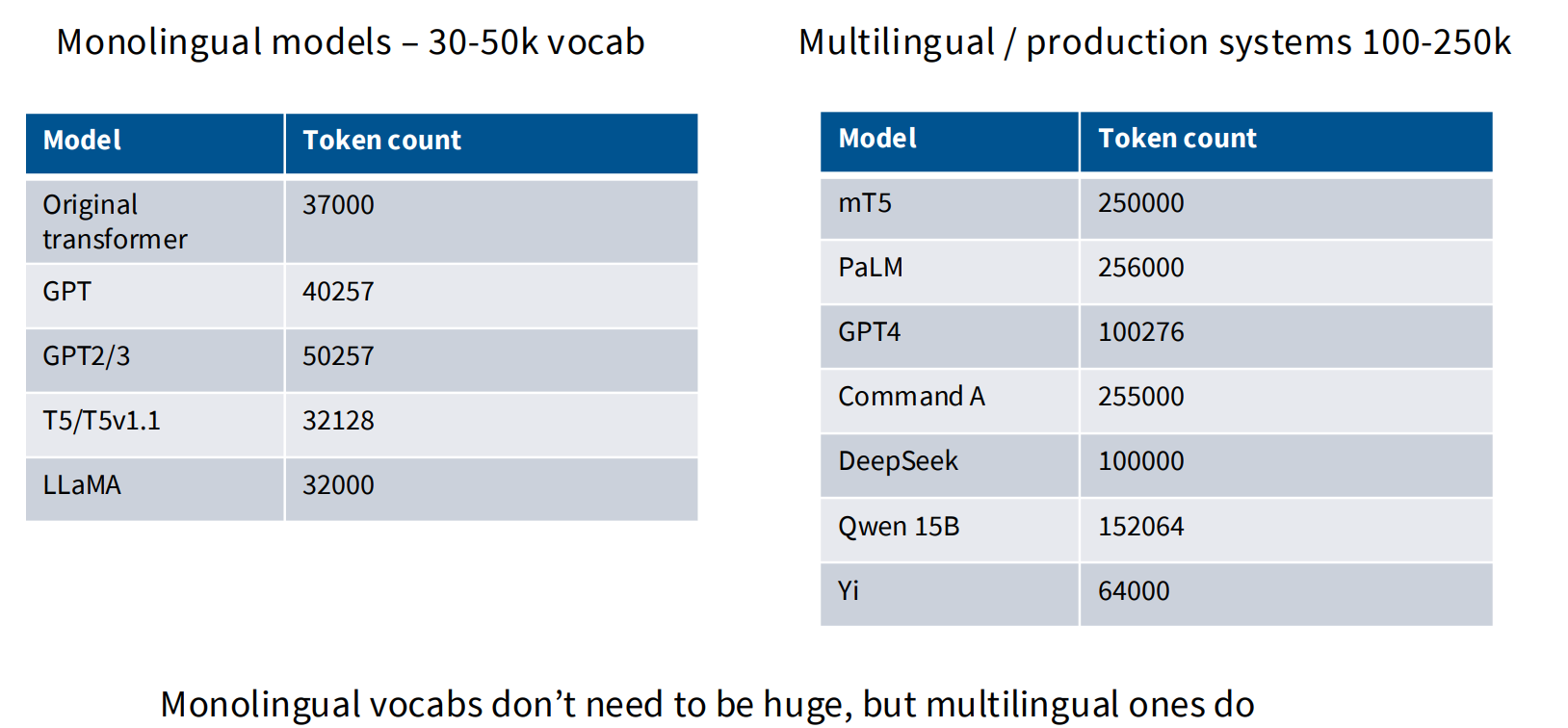
vocabulary size

单语言大概在四五w的量级。多语言大模型的词表大概在十几万到二十几万这样。 

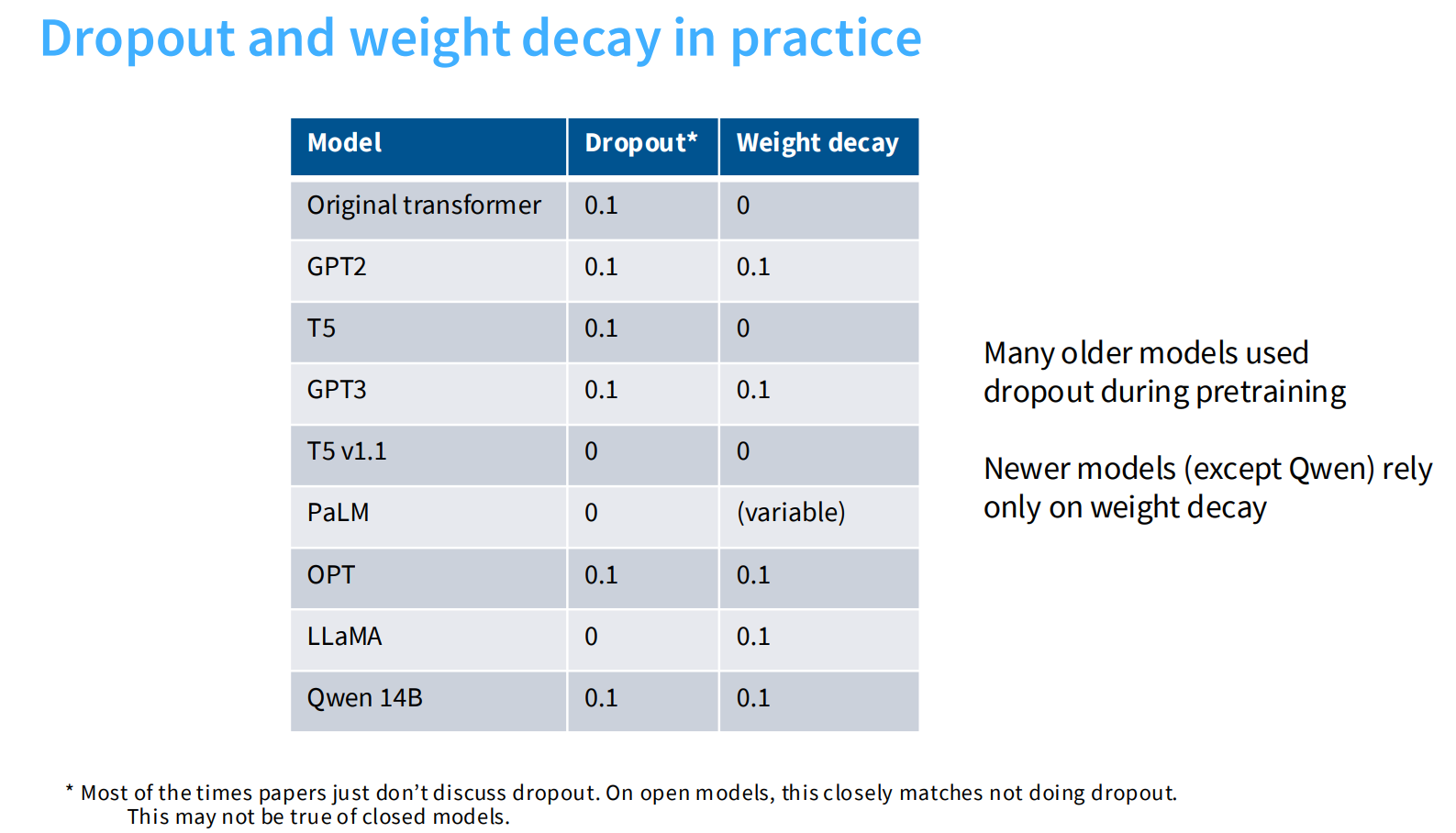
Dropout and other regularization

         似乎预训练用了大量的数据，而且基本只跑一个epoch，根本不会出现过拟合，这样是不是就不需要dropout？

        但事实上，dropout是之前常会用到的手段，近年来dropout使用场景变少，更加趋向于使用weight decay。但weight_decay实际使用的目的不是控制模型过拟合（图1可以看到，不同weight decay比例并不影响最终trainloss和val loss的比例）。

        图2和图3可以看到weight_decay会与优化器的学习率等产生非常复杂的作用（有decay的时候，当learning rate骤降的时候，模型的training loss也会骤降），实验结果可以看到设置weight decay的目的是为了得到更好的training_loss。

        非常反直觉的：通常来说加入weight_decay之后，模型的val_loss会降低，但实际上，trainingloss降低且和val_loss保持一致（图1）

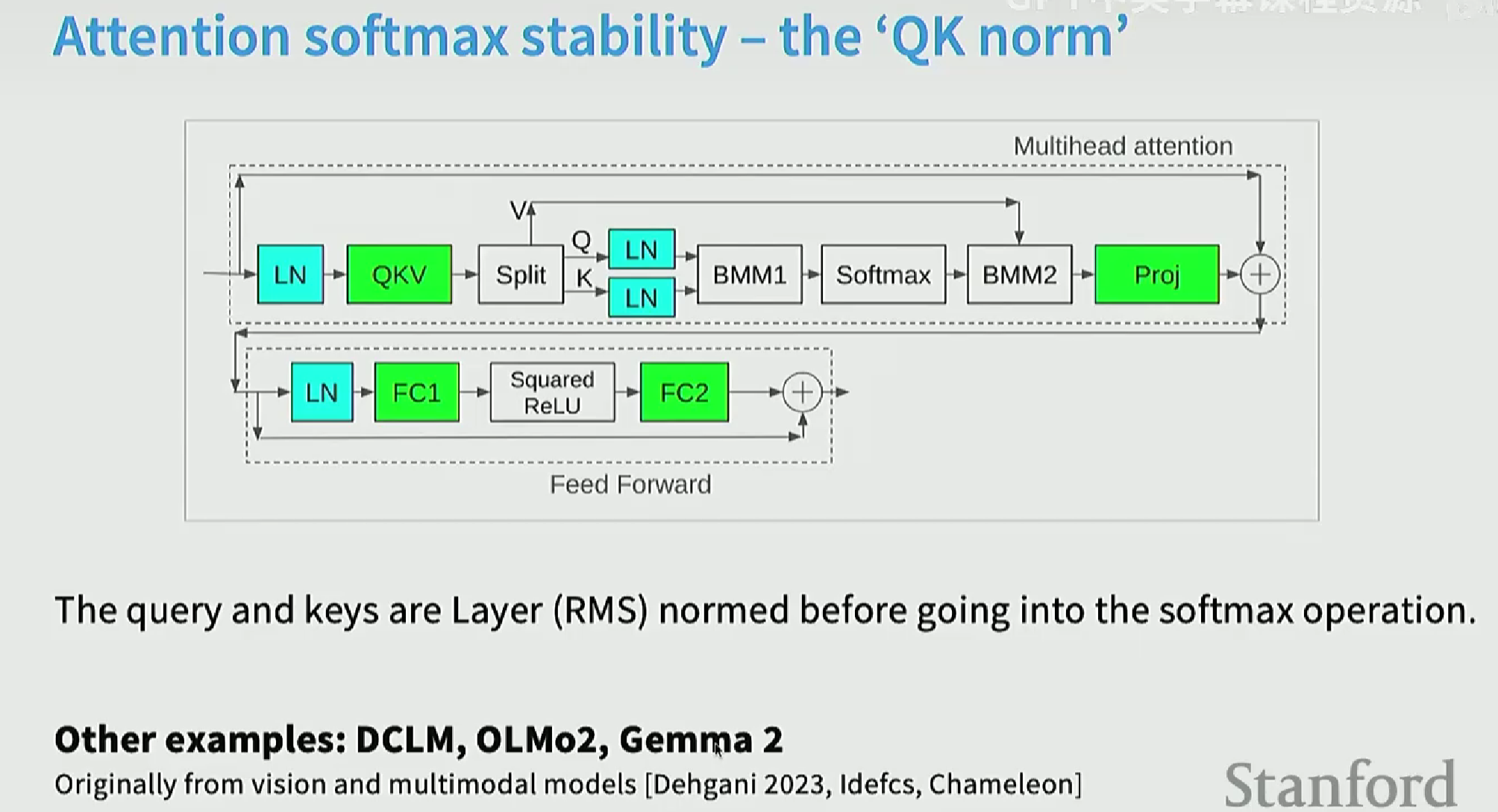
Stability tricks

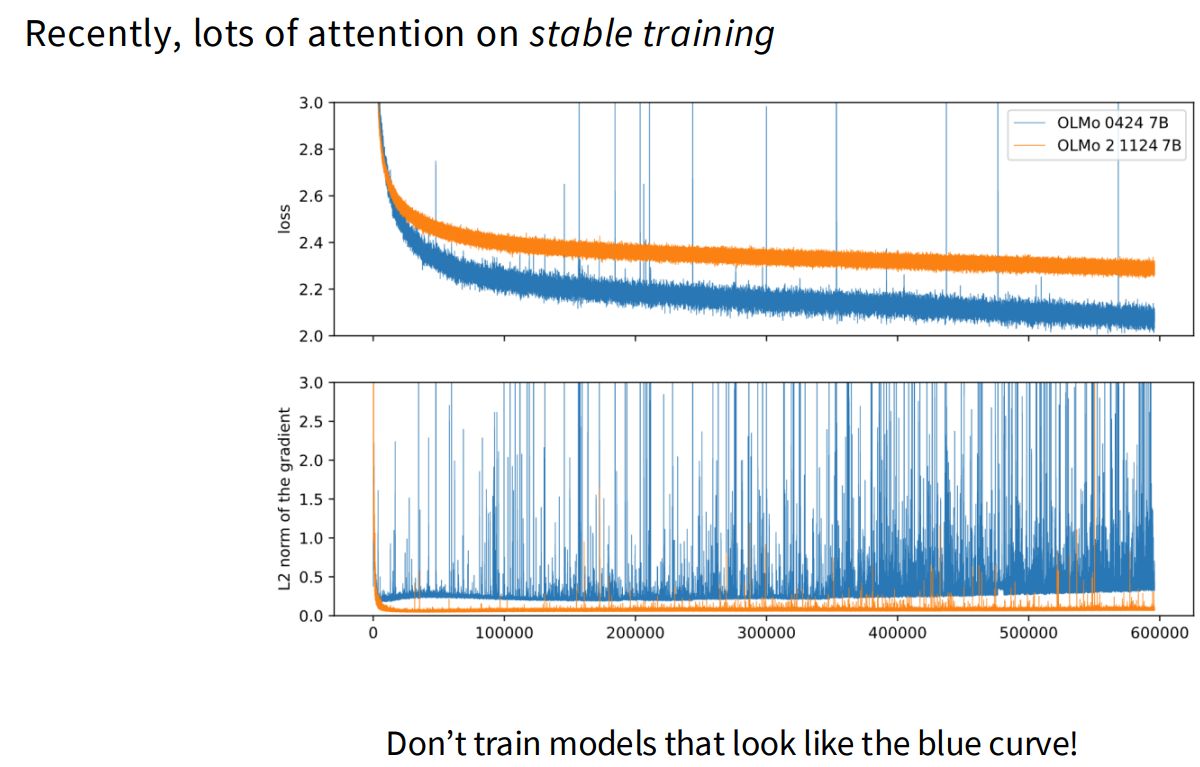
z-loss（控制softmax的输出）

QK-norm（控制softmax的输入）

layernorm不断加加加加加到厌倦~

 Logit soft-capping

总结： Soft-capping 是 “稳定性工具箱”中的一个（过时的）技巧。它虽然能有效防止 NaN 崩溃，但它既拖慢了训练速度，又损害了模型最终的质量，是一种“下下策”。它不如 Z-Loss（质量中性）或 QKV_norm（质量提升）等更现代的技巧。通常qk-norm的效果是最好的。

Attention heads

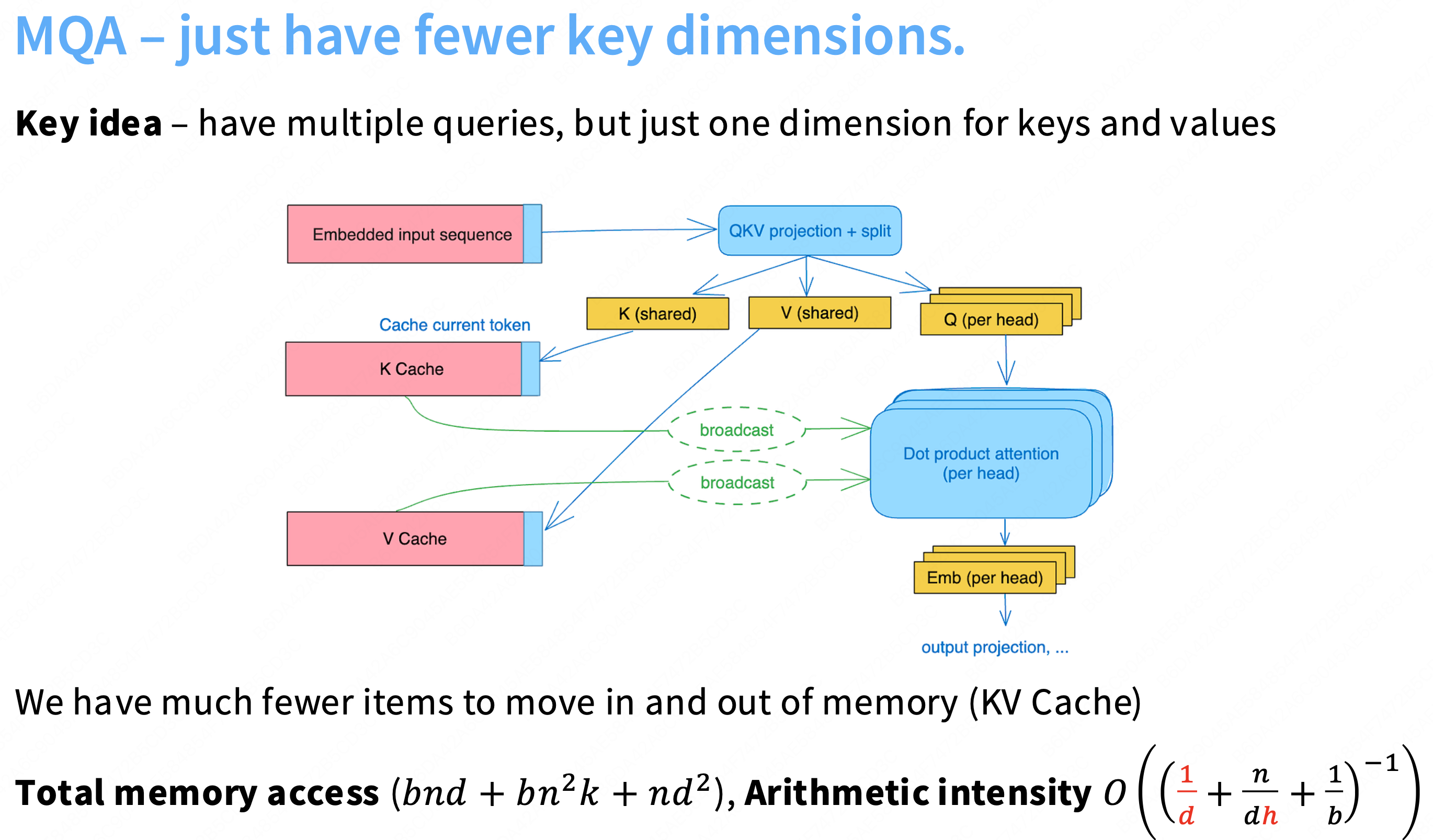
GQA/MQA – Reducing attention head cost

（可以把之前整理的gqa和mqa内容结合起来整理）

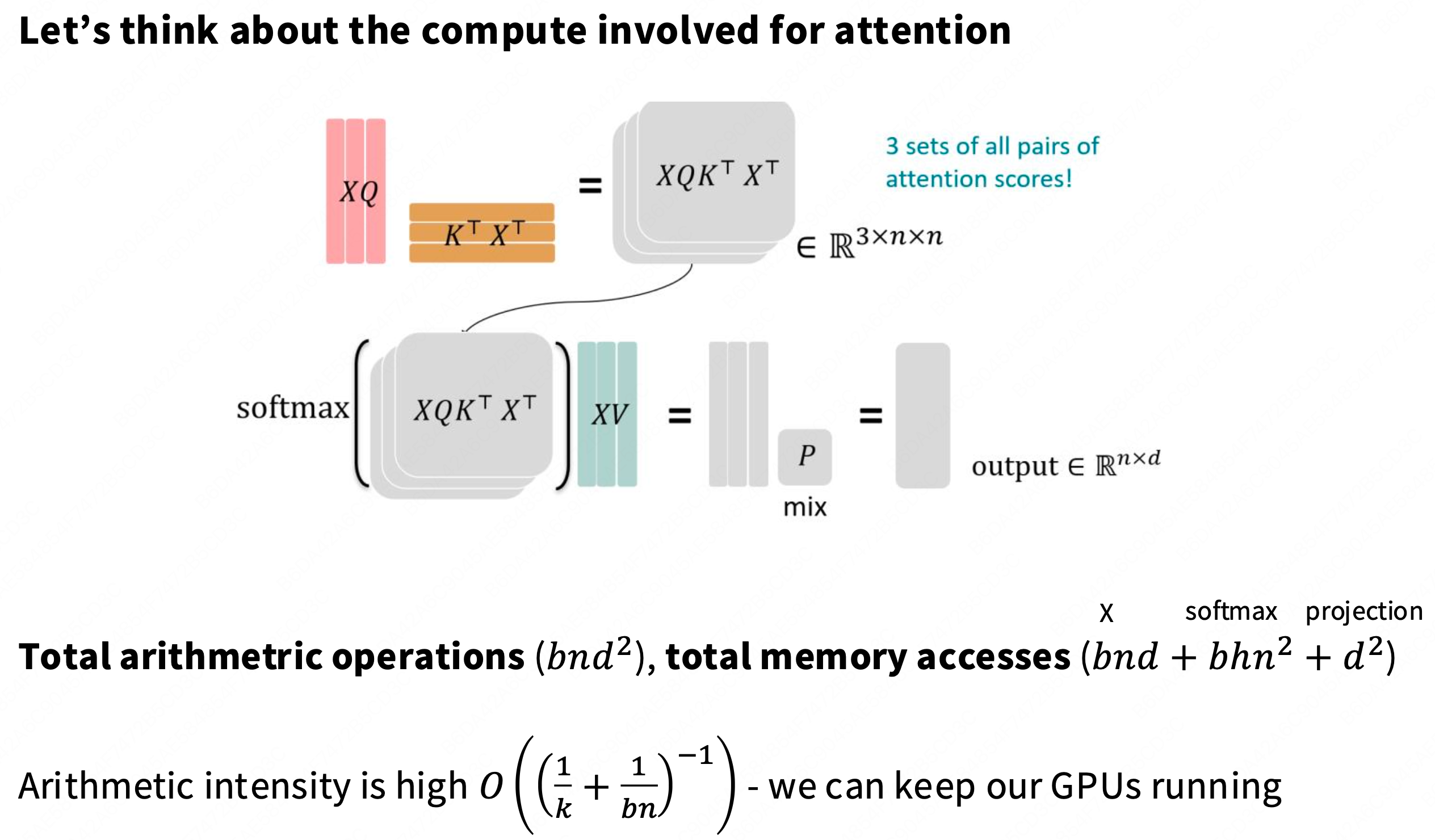
1. 核心问题：标准 MHA 的“推理瓶颈”

        我们“从零开始”构建的标准**多头注意力（MHA）架构在训练时是高效的。因为 Q@K.T 和 Scores@V 都是大型矩阵乘法，它们是“计算受限 (Compute-Bound)”的，可以跑满 GPU 的 MFU（模型利用率）。然而，MHA 在推理（Inference）时存在致命的性能瓶颈。

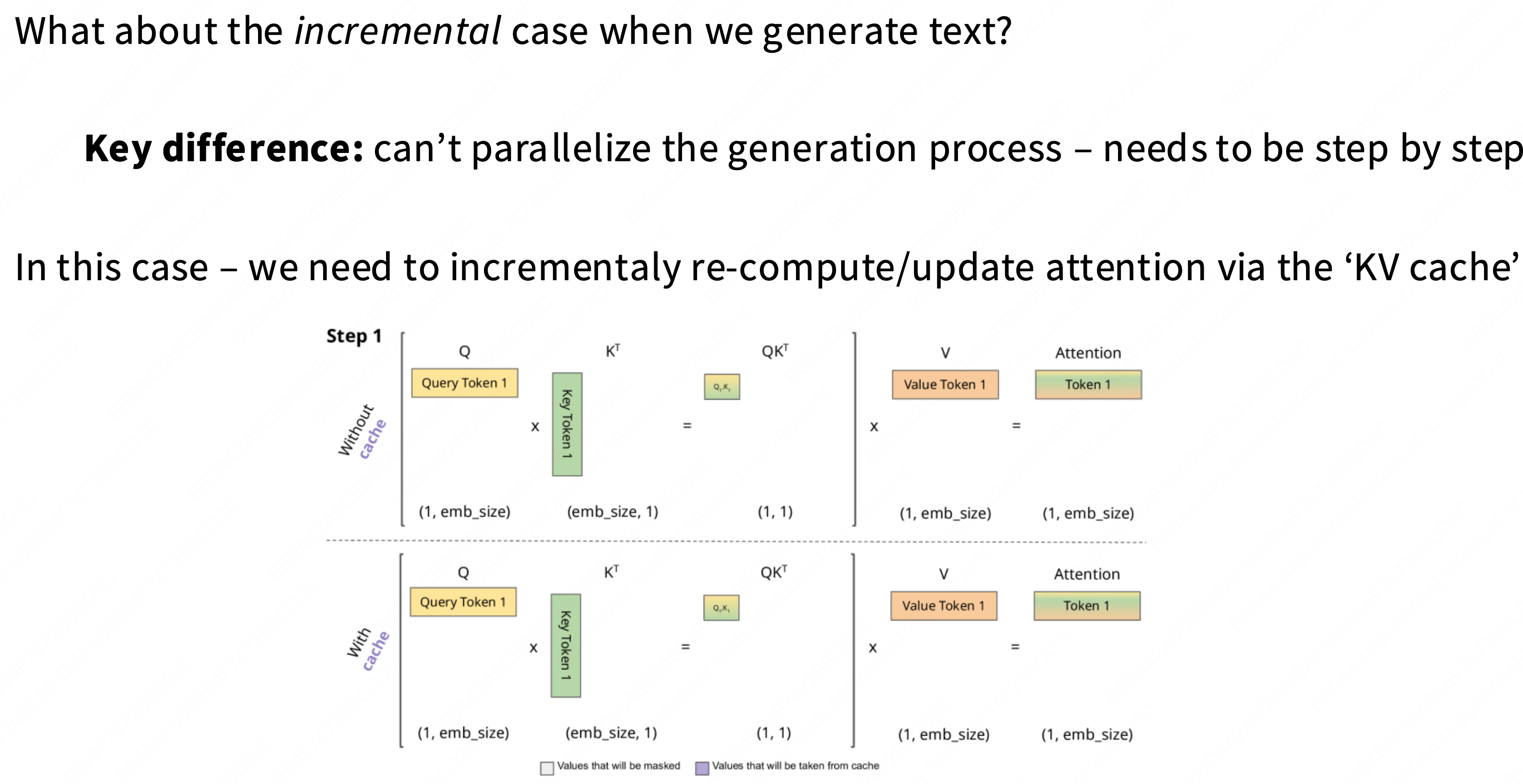
• 根本原因：

  • 文本生成（推理）是一个“自回归”（step-by-step）的过程，无法像训练那样并行化。为了避免在生成每个新 Token 时重复计算，我们必须使用一个“KV 缓存” (KV Cache)来存储所有历史 Token 的 Key 和 Value 向量。

• 瓶颈所在：

  • 在生成第 n 个 Token 时，GPU 必须从 VRAM（显存）中完整地读取所有 n-1 个历史 KV Cache。

  • 对于 MHA，每个 Query 头（h）都有自己专属的 K/V 头。这意味着 KV 缓存的大小是 (n-1)*h*d_k。

  • 当序列 n 很长或批量 b 很大时，这个 KV 缓存变得极其巨大。

  • 结果：在推理时，GPU 绝大部分时间都在“空转”，等待数据从 VRAM 缓慢地读取到计算核心。这个操作是“内存带宽受限 (Memory-Bandwidth-Bound)”的，计算强度（AI）极低，速度极慢。

2. 解决方案演进：MQA 与 GQ

  为了解决这个“内存带宽”瓶颈，核心思想是减少 K/V 头的数量，从而减小 KV 缓存的大小。

a) MQA：多查询注意力 (Multi-Query Attention)

• 架构： 这是一个“激进”的方案。它让所有的 H 个 Query 头共享同一组 K/V 头。

  • （H 个 Q-heads, 1 个 K-head, 1 个 V-head）

• 好处：

  • KV 缓存的大小瞬时减小了 H 倍。

  • 内存带宽压力极大缓解，推理速度（Time per sample）显著提升。

• 坏处：

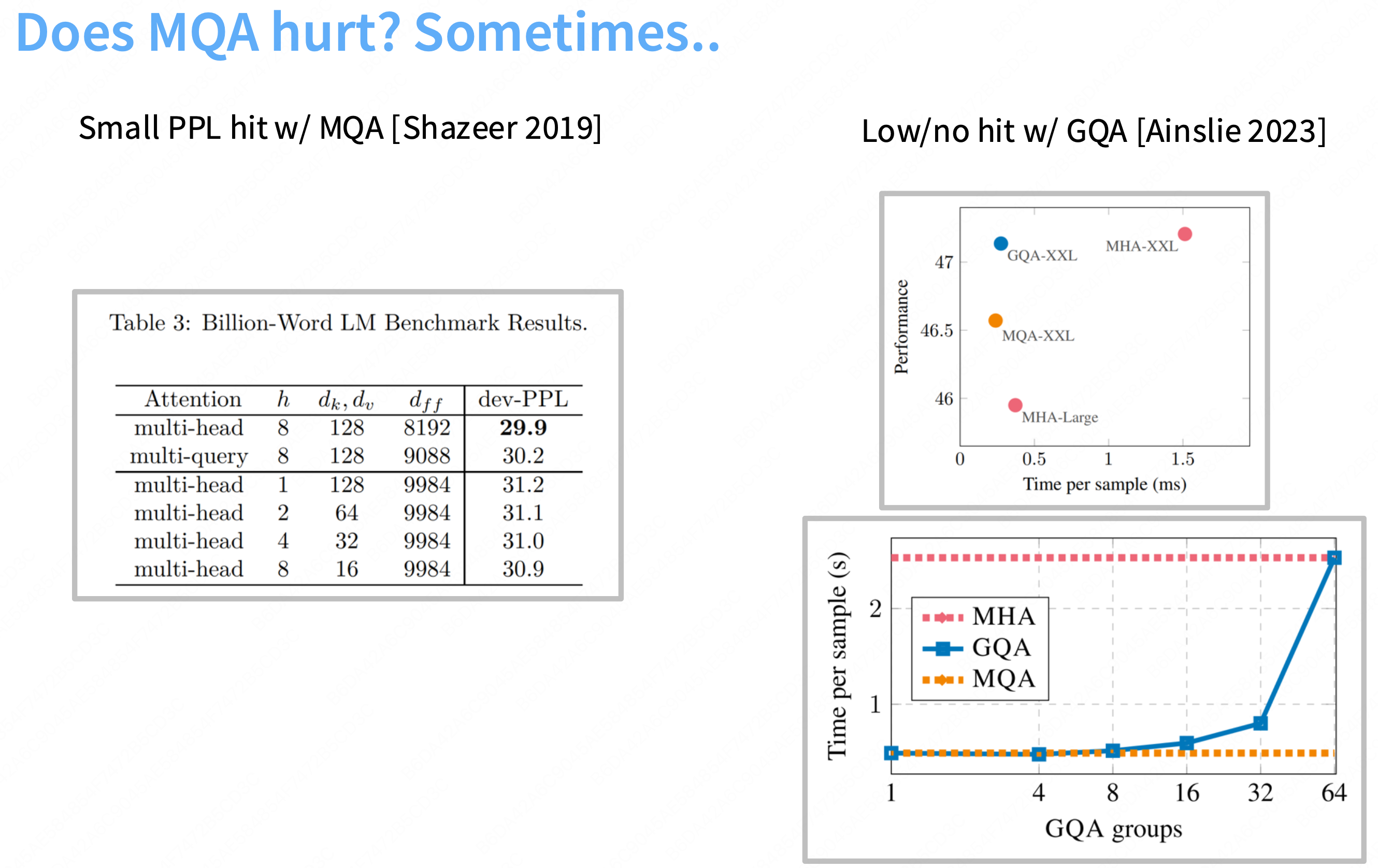
  • 这种“极致”的共享破坏了模型的表达能力。

  • 幻灯片中的表格显示，MQA 导致了“轻微的 PPL（困惑度）损失”（例如 30.2 vs 29.9），模型质量下降了。

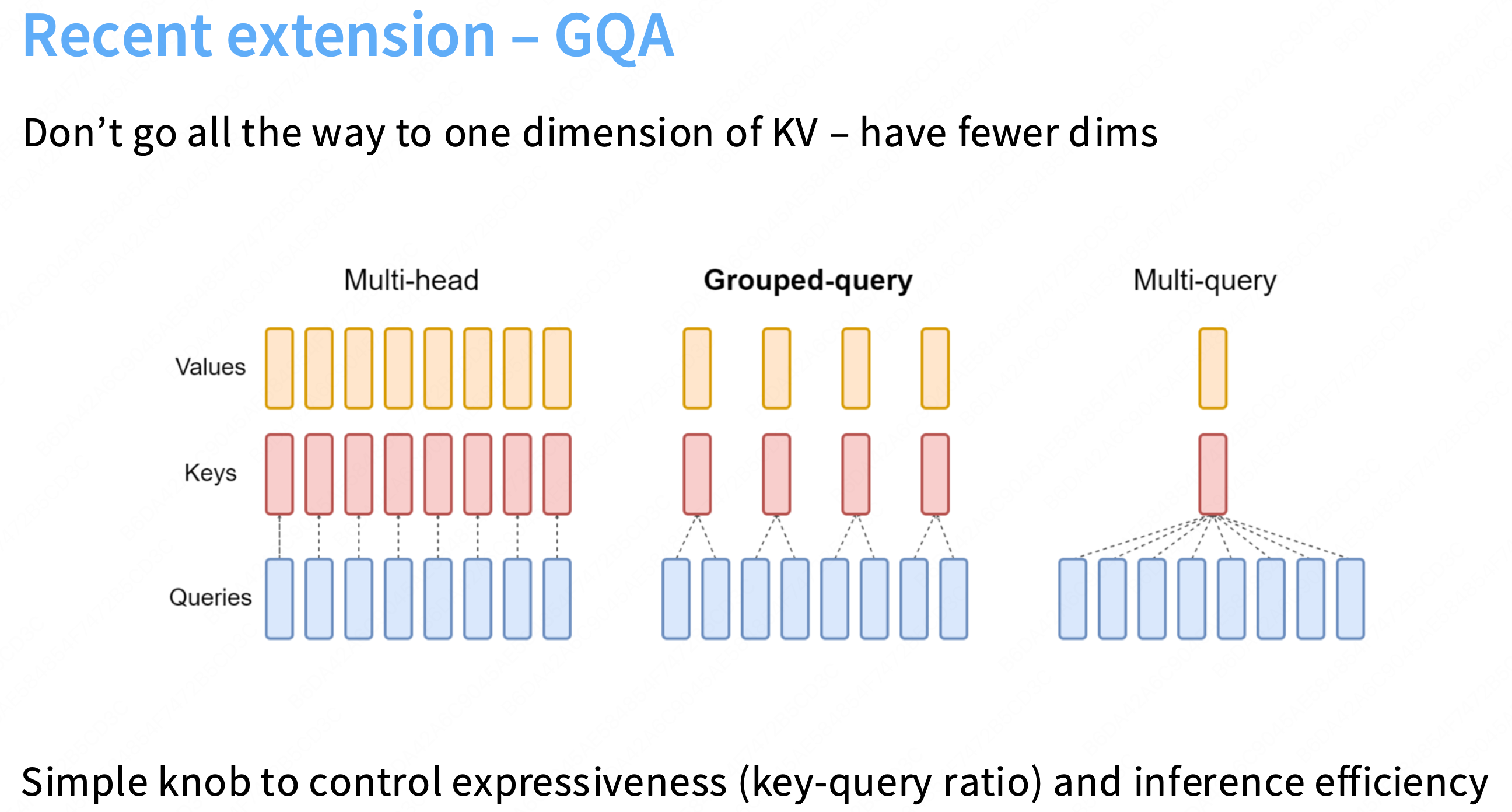
b) GQA：分组查询注意力 (Grouped-Query Attention)

• 架构： 这是 LLaMA 2, Mistral 等现代模型采用的“最佳折中”**方案。

• 核心思想： GQA 介于 MHA 和 MQA 之间。它将 H 个 Q-heads 分成 G 组，每组内的 Q-heads 共享同一组 K/V 头。

  • （H 个 Q-heads, G 个 K-heads, G 个 V-heads，其中 1 < G < H）

• 好处：GQA 实现了“两全其美”。

  • 1. 获得 MQA 的速度： 它仍然极大地压缩了 KV 缓存（H/G 倍），推理速度几乎与 MQA 一样快。

  • 2. 保持 MHA 的质量： 幻灯片中的图表显示，GQA（GQA-XXL）的性能（质量）与 MHA（MHA-XXL）几乎完全相同，没有质量损失。

        总结： GQA 通过“分组共享 K/V”的方式，在不牺牲模型质量的前提下，极大地减小了 KV 缓存大小，从而根本性地解决了 MHA 在推理时的内存带宽瓶颈，实现了 SOTA 级的推理速度。

Sparse  / sliding window attention

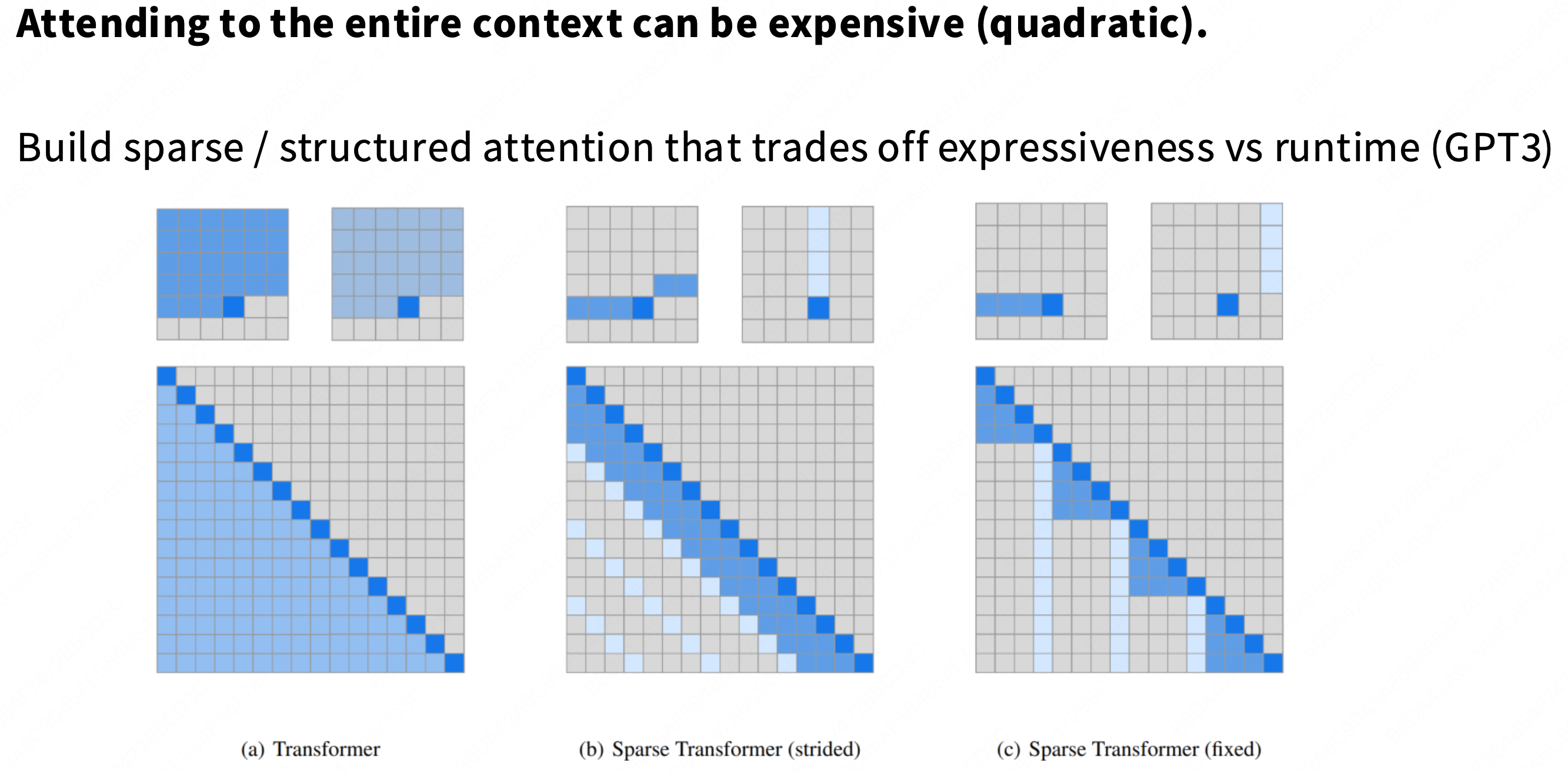
1. 核心问题：为什么“昂贵（Quadratic）”？

• (a) Transformer (标准)： 这是我们熟悉的标准**因果（Causal）注意力。

  • 它的“注意力矩阵” (Q@K.T) 是一个[L, L]的矩阵。

  • 在自回归（Autoregressive）解码时，一个 Token i 必须与所有在它之前的 Token 1...i 进行点积计算。

  • 计算复杂度： O(L^2)。

• 灾难性的后果：

  • 序列长度 L 从 1024 翻倍到 2048，计算/内存开销不是 2 倍，而是 4 倍。

  • 从 1024 增长 10 倍到 10240，开销暴增 100 倍。

  • 这使得在非常长的上下文（如 10 万个 Token）上使用“标准”注意力在计算上变得不可行。

2. 解决方案：“稀疏”带来的权衡

“Build sparse / structured attention that trades off expressiveness vs runtime (GPT3)”

• 核心思想： 我们“牺牲”（trade off）一部分“表达能力”（Expressiveness），来换取“运行时”（Runtime）的巨大提升。

• 牺牲什么？ 我们强行规定一个 Token 不再能“看到”所有的历史 Token。

• 得到什么？ 计算复杂度从 O(L^2) 降低到更线性的 O(L \log L)或 O(L \sqrt{L})。

这张幻灯片展示了两种（在 GPT-3 论文中探索过的）稀疏模式：

b) 稀疏 Transformer (Strided - 步进式)

• 结构：

  1. 局部（Local）注意力： Token i 只能看到它附近的（例如 k=128 个）Token（图中的“对角线带”）。

  2. 步进（Strided）注意力： Token i 还能看到每 s 个 Token（例如，每 16 个 Token 中的第 1 个）。

• 动机： 假设模型主要依赖“局部”信息，但偶尔需要“跳”很远去回顾一个（步进的）“全局”概览。

c) 稀疏 Transformer (Fixed - 固定式)

• 结构：

  1. 局部（Local）注意力： 同样，Token i 只能看到它附近的 k 个 Token。

  2. 固定（Fixed）注意力： Token i 还能看到序列最开头的 p 个 Token（例如，前 32 个 Token）。

• 动机： 假设序列的“开头”（例如，一个系统提示 system prompt 或一个文档的摘要）包含了对整个序列都至关重要的“全局上下文”，所有后续 Token 都应能随时回顾它们。

3. 总结

这张幻灯片展示了解决O(L^2)问题的**“早期思想”：通过“固定的稀疏掩码” (Static Sparse Masks)来减少计算。

• 权衡： 这是一种“硬编码”的妥协。我们赌模型不需要“全连接”的注意力，而 (b) 和 (c) 这种模式“足够好”。

• 历史（GPT-3）： 尽管 GPT-3 论文探索了这些，但最终发布的模型（如 davinci）为了追求最高质量，还是使用了（昂贵的）标准“(a) 稠密注意力”。

• 现代 SOTA（如 Mistral, LLaMA 2）：

  • Sliding Window Attention (SWA)： 现代模型（如 Mistral 7B）发现，一个极简的 (b) 或 (c) 版本——即只保留“局部注意力”（那个对角线带）——在实践中效果惊人地好。

  • FlashAttention： 彻底改变了游戏规则。FlashAttention 并没有减少O(L^2)的计算量，但它通过 GPU 内核融合技术，解决了 O(L^2)的内存（VRAM）瓶颈。这使得（a）标准稠密注意力在更长的序列上（例如 8K, 16K）变得可行。

Sliding window attention

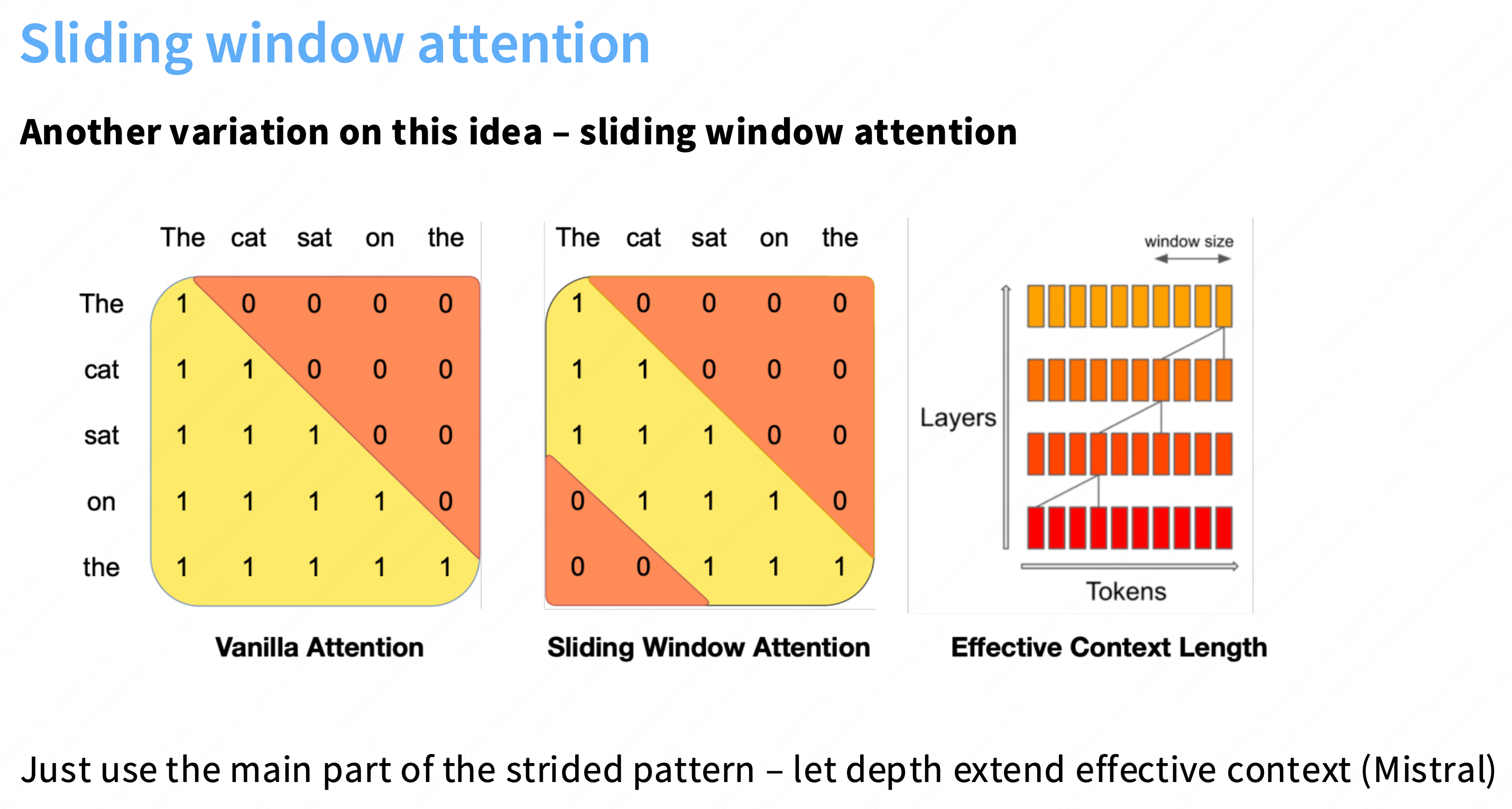
1. 核心概念：滑动窗口注意力 (SWA)

• 对比 (左, Vanilla Attention):

  • 在标准的因果（causal）注意力中，Token "the"（位置5）必须与所有之前的 4 个 Token（1, 2, 3, 4）进行计算。

  • 这是 O(L^2) 复杂度的来源。

• SWA (中, Sliding Window Attention):

  • 我们设置一个固定大小的“窗口” W（例如 W=3）。

  • Token "the"（位置5）现在被强行限制，只允许与它窗口内的 Token（"sat", "on"，即位置 3, 4）进行计算。

  • 它无法再看到 "The" (位置1) 或 "cat" (位置2)。

• 巨大的性能优势 (最重要的)：

  • 这种注意力的计算复杂度不再是 O(L^2)。

  • 它变成了 O(LW)。由于 W 是一个常数（例如 4096），它远远小于 L（例如 128,000），因此总复杂度从“二次方”降低到了“线性” O(L)！

  • 这使得在极长的上下文（100k+ Token）上进行训练和推理在计算上成为可能。

2. SWA 的“魔力”：如何解决“短视”问题？

        SWA 似乎有一个致命缺陷：如果 W=4096，那么 Token 5000 永远无法看到 Token 1 的信息。这不就丢失了所有远距离依赖吗？

        答案（右, Effective Context Length）：不会，因为我们有“深度” (Depth)。

• 幻灯片底部的注释： “Just use the main part of the strided pattern – let depth extend effective context (Mistral)”

• 工作原理：

  • 在第 1 层 (Layer 1)：Token 5000 只能看到 [Token 904 ... Token 4999]（假设 W=4096）。

  • 在第 2 层 (Layer 2)：Token 5000 仍然只能看到 [Token 904 ... Token 4999]（在第2层的表示）。但是，Token 4999 在第 2 层的表示，是它在第 1 层查看它的窗口（[Token 808 ... Token 4998]）后计算出来的。

  • 信息“跳跃”：Token 808 的信息在第 1 层被 Token 4999“读取”。Token 4999 的（混合了 808 信息的）表示，在第 2 层被 Token 5000“读取”。

• 结论： 尽管 SWA 在单层（Single Layer）的视野是“短视”的（W），但信息会随着层数（n_layer）的增加而“逐层跳跃”。一个 32 层的模型，其“有效上下文长度” (Effective Context Length)可以远大于 W（理论上可达 W*n_layer）。

思考题

• 问题：GQA / MQA 和 Sparse Attention (SWA) 是“互斥”还是“正交”的？

        答案： 它们是 100% 正交（Orthogonal）且完全兼容的。它们解决的是两个完全不同的性能瓶颈：

1. SWA (Sparse Attention):

   • 解决什么： 解决 Q@K.T 矩阵的O(L^2)计算复杂度问题。

   • 何时： 在训练和推理中都有效。

   • 方式： 减少计算量（FLOPs）。

2. GQA / MQA:

   • 解决什么： 解决推理时的 KV 缓存的内存带宽问题。

   • 何时： 仅在推理时有效。

   • 方式： 减少内存读写量（I/O）。

结论：

        一个 SOTA（State-of-the-Art）的长上下文模型（如 Mistral, LLaMA 2 Long）会同时使用这两种技术：使用 SWA 来训练（使其在 O(L) 时间内处理 32k 上下文）；使用 GQA 来推理（使其在长上下文 KV 缓存下仍能快速生成）。

补充-交错注意力机制

        SWA（滑动窗口）太“短视”，信息“逐层跳跃”太慢。我们如何能低成本地（保持 O(L) 效率）又高效率地（Token30,000 直接访问 Token 10）获取全局信息？这张幻灯片展示的“交错注意力”（Interleaved Attention）（由 Cohere, LLaMA 4, Gemma 等模型使用）

1. 核心技巧：“全”注意(Full)与“滑”注意(SWA)相交错

        这个技巧不再试图用“一种”注意力机制解决所有问题，而是做了一个“混合”（Hybrid）设计，以实现“速度”和“质量”的最佳权衡**。

• 问题：

  1. SWA（滑动窗口）：速度快（O(L)），但质量差（“短视”，全局信息传递慢）。

  2. Full Attention（全注意力）：质量高（“长视”，Token i 能看所有 Token j），但速度慢（O(L^2)，计算灾难）。

• 解决方案（如 Cohere Command A 所示）：

  • 大部分层 (如 1, 2, 3)：使用快速的 SWA。

    • 作用： 处理绝大多数的“局部”信息（例如，一个词和它附近的词的关系）。这保持了整个模型的高吞吐量（time_per_step 快）。

  • 少数层 (如每 4 层)：插入一个昂贵的 Full Attention（全注意力）层。

    • 作用： 充当一个“全局信息路由器”。在这一层，Token 30,000 被允许（不惜代价地）直接回顾 Token 10。代价：这一层的计算是O(L^2)，非常慢。

• 最终的权衡：

  • 整个模型的总计算量不再是O(L^2)（太慢）或O(L)（太“短视”）。

  • 它的计算量是 (N-k) * O(L) + k * O(L^2)（其中 k 很小，例如 N/4）。

  • 我们通过“忍受”几个昂贵的 O(L^2)层，换来了 SWA 无法提供的直接全局信息交换，从而极大提升了长上下文任务的模型质量。

2.“微妙”细节（RoPE vs NoPE）

这张幻灯片还揭示了两种不同的“混合”实现哲学：

1. Cohere Command A 的实现：

   • SWA 层： 使用 RoPE（旋转位置嵌入）。RoPE 是相对位置编码，非常适合 SWA 的“局部”窗口。

   • Full 层： 使用 NoPE（无位置嵌入）。这是一个大胆的设计。Cohere 认为，当信息到达第 4 层时，其“位置”信息已经完全融入了 Token 的表示中。这一层（Full）的唯一工作是进行“纯粹的、内容级别的”信息混合，而不应该再被“位置”所干扰。

2. LLaMA 4 / Gemma 的实现：

   SWA 层 + Full 层： 两者都使用 RoPE。这是更“直观”的设计。它允许 Full Attention 层也能感知到长距离的相对位置（例如，RoPE(30000) - RoPE(10)），这在理论上更强大。

总结：“交错注意力”（SWA + Full）是模型在“长上下文”（L 很大）和“计算可行性”之间找到的最佳平衡点。