Remmarguts' Date POJ - 2449(K短路问题+A*)

K短路问题与A*算法

最新推荐文章于 2020-11-02 22:32:14 发布

原创最新推荐文章于 2020-11-02 22:32:14 发布 · 229 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#k短路问题+A*

本文深入探讨了K短路问题的解决方案，详细解析了如何利用改进的Dijkstra算法和A*算法找到从起点到终点的第K条最短路径。通过引入估价函数优化搜索过程，减少无效节点的访问，提高算法效率。

题意：传送门
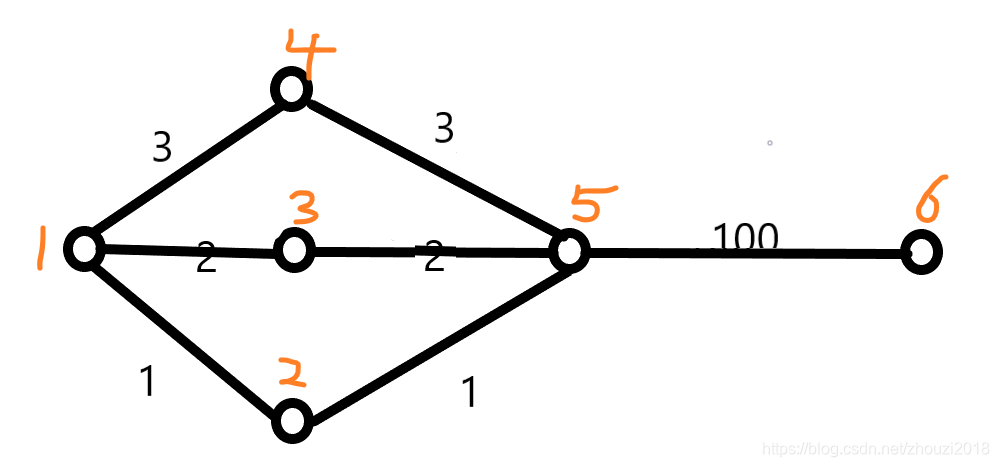
题解：K短路问题，以前只会套板子，现如今感觉了解了更多了，首先最基本的 $d i j k s t r a$ 算法，如果某个队头从优先队列中取出时，证明它此时是从起始点到它的最短路，那么如果我们不加入那些限制，遇到就加入队列，如果某个节点第 $i$ 次从队头中取出时，就证明此时的距离是从开头到这个点的第 $i$ 短路了，然后再想下从 $S - > T$ 的最短路中，如果中间某个点出队超过 $k + 1$ 次，那么必然不用拓展它了，因为答案必然不会在它之后的更新中，现在考虑这种方式找第 $k$ 短路的缺陷在这里插入图片描述
像上图这样，如果此时要求 $1 - > 6$ 的第 $2$ 短路，稍微看下都知道是 $1 - > 3 - > 5 - > 6$ ，但是这个 $5$ 号点会在第 $3$ 次入队后依然 $6$ 一次也没有弹出，这样的情况当然需要避免，我们想要的是依次弹出，不是使得大量无用的点一直入队出队，所以引入了估价函数 $f [i]$ ，本题中的估价函数直接建立反图，然后求出每个点到 $t$ 点的距离即可，之后每次搜索时以 $d i s + f [i]$ 为关键字进行排序，这样就显得智能了很多，使得走的偏路更少，看上图就能看出，第一次就是将 $1 - > 2 - > 5 - > 6$ 依次走一遍，接着再走 $1 - > 3 - > 5 - > 6$ ，使得很多节点访问次数远小于 $k$ 。
$c o d e :$

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#define pii pair<int,int>
#define piii pair<int,pair<int,int>>
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int N=1e3+5;
const int M=2e5+5;
struct edge{
    int u,v,w,next;
};
edge edges[M];
int head[N],rhead[N],tot;
void init()
{
    memset(head,-1,sizeof head);
    memset(rhead,-1,sizeof rhead);
    tot=0;
}
void add_edges(int u,int v,int w)
{
    edges[tot].u=u;edges[tot].v=v;edges[tot].w=w;edges[tot].next=head[u];head[u]=tot++;
}
void add_redges(int u,int v,int w)
{
    edges[tot].u=u;edges[tot].v=v;edges[tot].w=w;edges[tot].next=rhead[u];rhead[u]=tot++;
}
int n,m,u,v,w,s,t,k,f[N],st[N];
void dijkstra()
{
    memset(st,0,sizeof st);
    memset(f,0x3f,sizeof f);
    f[t]=0;
    priority_queue<pii,vector<pii>,greater<pii> >heap;
    heap.push(make_pair(0,t));
    while(!heap.empty()){
        pii t=heap.top();
        heap.pop();
        int u=t.second;
        if(st[u])continue;
        st[u]=1;
        for(int i=rhead[u];~i;i=edges[i].next){
            int v=edges[i].v,w=edges[i].w;
            if(f[v]>f[u]+w){
                f[v]=f[u]+w;
                heap.push(make_pair(f[v],v));
            }
        }
    }
}
int a_star()
{
    memset(st,0,sizeof st);
    priority_queue<piii,vector<piii>,greater<piii> >heap;
    heap.push(make_pair(f[s],make_pair(0,s)));
    while(!heap.empty()){
        piii tmp=heap.top();
        heap.pop();
        int u=tmp.second.second,dis=tmp.second.first;
        if(st[u]>=k)continue;
        st[u]++;
        if(u==t&&st[u]==k)return dis;
        for(int i=head[u];~i;i=edges[i].next){
            int v=edges[i].v,w=edges[i].w;
            if(st[v]<k){
                heap.push(make_pair(f[v]+dis+w,make_pair(dis+w,v)));
            }
        }
    }
    return -1;
}
int main()
{
    n=read();m=read();
    init();
    for(int i=0;i<m;i++){
        u=read();v=read();w=read();
        add_edges(u,v,w);
        add_redges(v,u,w);
    }
    s=read();t=read();k=read();
    if(s==t)k++;
    dijkstra();
    printf("%d\n",a_star());
    return 0;
}