本文主要介绍冒泡排序算法，阐述其原理，即操作相邻元素，通过多次冒泡使元素有序，还可优化。分析了其效率，包括空间复杂度为O(1)，是原地稳定排序算法，最好、最坏和平均时间复杂度均为O(n^2)。给出了C++、Golang、Java的实现示例，并总结了排序特点。
理论
冒泡排序只会操作相邻的两个元素。每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置，重复n次，就完成了n个数据的排序工作。
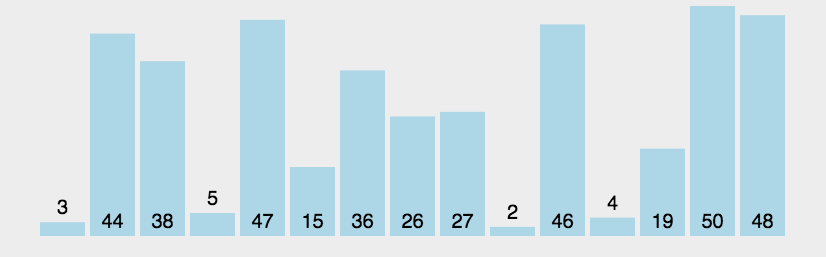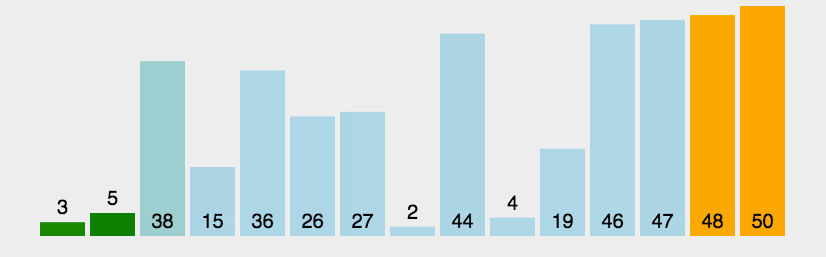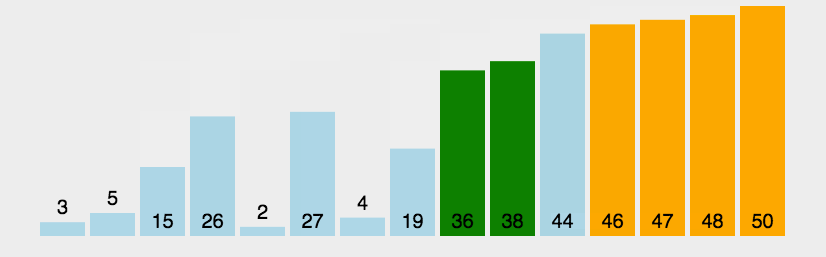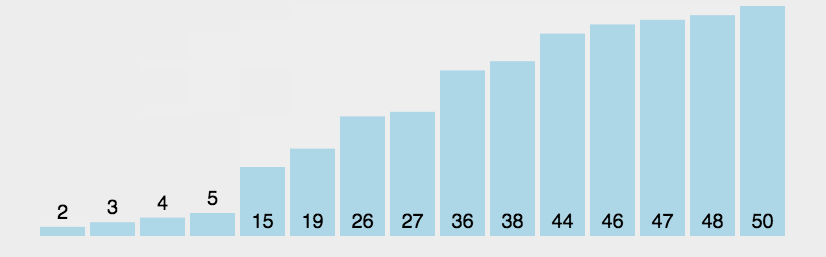
举个例子：
- 我们要对一组数据 4，5，6，3，2，1，从小到到大进行排序。第一次冒泡操作的详细过程就是这样：
- 可以看出，经过一次冒泡操作之后，6 这个元素已经存储在正确的位置上。要想完成所有数据的排序，我们只要进行 6 次这样的冒泡操作就行了。
- 实际上，刚才讲的冒泡排序还可以优化。当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后继的冒泡操作。再举个例子，，这里面给 6 个元素排序，只需要 4 次冒泡操作就可以了。
效率分析：
（1）冒泡排序是原地排序算法吗？
冒泡的过程只涉及相邻数据的交换操作，只需要常量级的临时空间。所以它的空间复杂度为O(1)，是一个原地排序算法。
（2）冒泡排序是稳定的排序算法吗？
在冒泡排序中，只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性，当有相邻的两个元素大小相等的时候，我们不做交换，相同大小的数据在排序前后不会改变顺序，所以冒泡排序是稳定的排序算法。
（3）冒泡排序的时间复杂度是多少？
- 最好情况下，要排序的数据已经有序了，我们只需要进行一次冒泡操作，就可以结束了，所以最好情况时间复杂度是O(n)。而最坏情况是，要排序的数据刚好是倒序排列的，我们需要进行n次冒泡操作，所以最坏情况时间复杂度是O( n 2 n^2 n2)
- 从冒泡排序的算法可以看出，如果待排序的元素为正序，则只需要进行一趟排序，比较次数为(n-1)次，移动元素次数为0； 如果待排序的元素为逆序，则需要进行n-1趟排序，比较次数为 ( n 2 − n ) / 2 (n^2-n)/2 (n2−n)/2，移动次数为 3 ( n 2 − n ) / 2 3(n^2-n)/2 3(n2−n)/2，因此，冒泡排序算法的时间复杂度为O(n ^2)。由于其中的元素移动比较多，所以属于内排序中速度较慢的一种。
那平均情况下的时间复杂是多少呢？
- 对于包含n个数据的数组，这n个数据就有n!中排序方式。不同的排序方式，冒泡排序执行的时间肯定是不同的。。如果用概率论方法定量分析平均时间复杂度，涉及的数学推理和计算就会很复杂。一种新的思路是通过“有序度”和“逆序度”这两个概念来进行分析。
- 有序度是数组中具有有序关系的元素对的个数。有序元素对用数学表达式表示就是这样：
有 序 元 素 对 ： a [ i ] < = a [ j ] ， 如 果 i < j 有序元素对：a[i]<=a[j]，如果i<j 有序元素对：a[i]<=a[j]，如果i<j
-
同理，对于一个倒序排列的数组，比如 6，5，4，3，2，1，有序度是 0；对于一个完全有序的数组，比如 1，2，3，4，5，6，有序度就是n*(n-1)/2，也就是 15。我们把这种完全有序的数组的有序度叫作满有序度。
-
逆序度的定义正好跟有序度相反（默认从小到大为有序）
逆 序 元 素 对 ： a [ i ] > a [ j ] , 如 果 i < j 逆序元素对：a[i] > a[j], 如果 i < j 逆序元素对：a[i]>a[j],如果i<j -
关于这三个概念，我们还可以得到一个公式：逆序度 = 满有序度 - 有序度。我们排序的过程就是一种增加有序度，减少逆序度的过程，最后达到满有序度，就说明排序完成了。
-
举个例子，要排序的数组的初始状态是 4，5，6，3，2，1 ，其中，有序元素对有 (4，5) (4，6)(5，6)，所以有序度是 3。n=6，所以排序完成之后终态的满有序度为 n*(n-1)/2=15。
- 冒泡排序包含两个操作原子，比较和交换。每交换一次，有序度就加1。不管算作怎么该，交换次数总是确定的，即为逆序度，也就是n*(n-1)/2–初始有序度。此例中就是 15–3=12，要进行 12 次交换操作。
- 对于包含n个数据的数组进行冒泡排序，平均交换次数是多少呢？最坏情况下，初始状态的有序度是0，所以要进行 n ∗ ( n − 1 ) / 2 n*(n-1)/2 n∗(n−1)/2次交换。最好情况下，初始状态的有序度是 n ∗ ( n − 1 ) / 2 n*(n-1)/2 n∗(n−1)/2，就不需要交换。我们可以取个中间值 n ∗ ( n − 1 ) / 4 n*(n-1)/4 n∗(n−1)/4，来表说初始有序度不是很高也不是很低的平均情况。
- 换句话说，平均情况下，需要 n ∗ ( n − 1 ) / 4 n*(n-1)/4 n∗(n−1)/4次交换操作，比较操作肯定要比交换操作多，而复杂度的上限是 O ( n 2 ) O(n^2) O(n2)，所以平均情况下的时间复杂度就是 O ( n 2 ) O(n^2) O(n2)
- 这个平均时间复杂度推导过程其实并不严格，但是很多时候很实用，毕竟概率论的定量分析太复杂，不太好用。
这三种时间复杂度为 O(n^2 ) 的排序算法中，冒泡排序、选择排序，可能就纯粹停留在理论的层面了，学习的目的也只是为了开拓思维，实际开发中应用并不多，但是插入排序还是挺有用的。
实现
C++
#include <iostream>
#include <list>
#include <vector>
#include <map>
template<typename T>
std::ostream& print(std::ostream &out,T const &val) {
return (out << val << " ");
}
template<typename T1,typename T2>
std::ostream& print(std::ostream &out,std::pair<T1,T2> const &val) {
return (out << "{" << val.first << " " << val.second << "} ");
}
template<template<typename,typename...> class TT,typename... Args>
std::ostream& operator<<(std::ostream &out,TT<Args...> const &cont) {
for(auto&& elem : cont) print(out,elem);
return out;
}
void bubbleSort(std::vector<int> &vec){
if(vec.size() <= 1){
return;
}
bool is_swap = false;
for (int i = 0; i < vec.size(); ++i) {
is_swap = false;
for (int j = 1; j < vec.size() - i; ++j) {
if(vec[j - 1] < vec[j]){
std::swap(vec[j - 1], vec[j]);
is_swap = true;
}
}
if(!is_swap){
break;
}
}
}
int main() {
std::vector<int> vec = {1,9,2,8,3,7,4,6,5,10, -1};
bubbleSort(vec);
std::cout << vec;
return 0;
}
实现过程如下：
#include <iostream>
#include <list>
#include <vector>
#include <map>
template<typename T>
std::ostream& print(std::ostream &out,T const &val) {
return (out << val << " ");
}
template<typename T1,typename T2>
std::ostream& print(std::ostream &out,std::pair<T1,T2> const &val) {
return (out << "{" << val.first << " " << val.second << "} ");
}
template<template<typename,typename...> class TT,typename... Args>
std::ostream& operator<<(std::ostream &out,TT<Args...> const &cont) {
for(auto&& elem : cont) print(out,elem);
out << "\n";
return out;
}
void swap(int & i, int &j){
int t = i;
i = j;
j = t;
}
void bubbleSort1(std::vector<int> &vec){
if(vec.empty() || vec.size() == 1){
return;
}
if(vec[0] < vec[1]){
swap(vec[0], vec[1]);
}
if(vec[1] < vec[2]){
swap(vec[1], vec[2]);
}
if(vec[3] < vec[4]){
swap(vec[3], vec[4]);
}
// ....
if(vec[8] < vec[9]){
swap(vec[8], vec[9]);
}
}
void bubbleSort2(std::vector<int> &vec){
if(vec.empty() || vec.size() == 1){
return;
}
for(int i = 0; i < vec.size(); i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
if(vec[0] < vec[1]){
swap(vec[0], vec[1]);
}
if(vec[1] < vec[2]){
swap(vec[1], vec[2]);
}
if(vec[3] < vec[4]){
swap(vec[3], vec[4]);
}
// ....
if(vec[7] < vec[8]){
swap(vec[7], vec[8]);
}
}
void bubbleSort3(std::vector<int> &vec){
if(vec.empty() || vec.size() == 1){
return;
}
for(int i = 0; i < 10; i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
for(int i = 0; i < 10 - 1; i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
for(int i = 0; i < 10 - 2; i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
for(int i = 0; i < 10 - 3; i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
// ...
for(int i = 0; i < 10-9; i++){
if(vec[i] < vec[i+1]){
swap(vec[i], vec[i+1]);
}
}
}
void bubbleSort66(std::vector<int> &vec){
if(vec.empty() || vec.size() == 1){
return;
}
for(int i = 0; i < vec.size(); i++){
for(int j = 0; j < vec.size() - i; j++){
if(vec[j] < vec[j+1]){
swap(vec[j], vec[j+1]);
}
}
}
}
void bubbleSort(std::vector<int> &vec){
if(vec.empty() || vec.size() == 1){
return;
}
bool flag = false;
for(int i = 0; i < vec.size(); i++){
for(int j = 0; j < vec.size() - i; j++){
if(vec[j] < vec[j+1]){
swap(vec[j], vec[j+1]);
flag = true;
}
}
if(!flag){
break;
}
}
}
int main() {
std::vector<int> vec = {1,9,2,8,3,7,4,6,5,10, -1};
bubbleSort(vec);
std::cout << vec;
return 0;
}
golang
package main
import (
"fmt"
)
// 假如我们只插入一个
func BubbleFindMax(arr [] int)int{
length := len(arr)
if length == 0 {
return -404;
}else if length == 1 {
return arr[0]
}else{
for i := 0; i < length - 1; i++ {
if arr[i] > arr[i + 1] {
arr[i], arr[i + 1] = arr[i + 1], arr[i];
}
}
return arr[length - 1];
}
}
func BubbleSort(arr [] int)[]int{
length := len(arr)
if length <= 1 {
return arr
}else{
for i := 0; i < length; i++ { // 有序元素个数， 从length到0
exchange := false;
for j := 0; j < length - 1 - i; j++ { // 每次都从头开始， 尾部是有序区
if arr[j] > arr[j + 1] {
arr[j], arr[j + 1] = arr[j + 1], arr[j];
exchange = true
}
}
if !exchange {
break
}
}
return arr;
}
}
func main() {
arr:=[]int {1,9,2,8,3,7,4,6,5,10, -1}
fmt.Println(BubbleSort(arr))
fmt.Println(arr)
}
java
从小到大：
1、定义一个10个int元素的数组。
2、从第一个元素开始，两个元素之间两两比较，哪个元素大就放到后面，一直比较到最后一个元素。
3、从第一个元素开始，两个元素之间两两比较，哪个元素大就放到后面，一直比较到倒数第二个元素。
4、。。。。。
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void bubbleSort2(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = false;
}
}
if (flag) {
break;
}
}
}
package array;
public class sort {
public static void main(String []args){
int []arr = {199, 11, 23, 56, 55, 49, 88};
BubbleSort(arr);
printArray(arr);
}
public static void bubbleSort(int [] array){
// 注意：如果array指向一个空指针，空指针是没有length属性的，因而会发生空指针异常
if (array == null || array.length < 2){
return;
}
for (int i = 0; i < array.length; i++){ //i 表示要排序n趟
boolean flag = true;
for (int j = 1; j < array.length - i; j++){ // 有序元素 0个, 1个[length-1], 2个[length-1, length-2] .....
if (array[j-1] > array[j]){ //比较相邻两个元素， 如果元素发生逆序
swap(array, j - 1, j);
flag = false; // 标记发生了交换
}
}
// 查看这一趟比数是否发生了交换， 如果没有发生交换，证明元素已经有序了
if (flag) {
break;
}
}
}
public static void swap(int []arr, int x, int y){
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
public static void printArray(int []arr){
for(int i=0;i<arr.length; i++){
if(i < arr.length - 1){
System.out.print(arr[i] + ",");
}else{
System.out.print(arr[i]);
}
}
System.out.println();
}
}
总结
1、有序区逐步扩大，无序区逐步缩小。
2、内循环用于比较，外循环用于控制有序区：刚开始有序区为0，因此内循环需要比较到最后一个元素，第二次比较有序区为1，因此内循环需要比较到倒数第二个元素。。。。
3、外循环控制要比较几趟[i表示第n趟]；内循环针对无序元素[0, length - 1 - i]比较：从第一个元素开始，比较两个相邻的元素，如果相邻元素的相对位置不正确，则进行交换，[如果正序，则什么也不干]，然后继续比较下面相邻两个元素。
结束条件：在任意一趟进行过程中，未出现交换。
4、冒泡排序法需要比较：10+9+8+7+6+5+4+3+2+1次
扫一扫
593
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
