算法：二叉搜索树转换为有序的双向链表

题目描述

请将二叉搜索树转换为有序的双向链表

比如，下面是一颗二叉搜索树

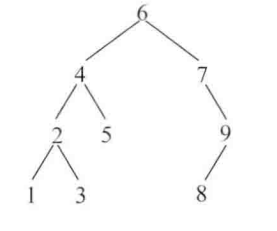
这颗二叉搜索树转换后的双向链表从头到尾是1~9。对每一个转换节点来说，原来的right指针等价于转换后的next指针，原来的left指针等价于转换后的last指针，最后返回转换后的双向链表的头结点

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};

class Solution {
  
public:
    TreeNode* convert(TreeNode* root) {

    }

};

题目解析

队列辅助

思路：

• 生成一个队列queue，按照中序遍历的顺序，将每个节点放入queue中
• 从queue中依次弹出节点，并按照弹出的顺序重连所有的节点即可

实现：

class Solution {
    void inOrderQueue(TreeNode* root, std::queue<TreeNode *> &queue){
        if(root == nullptr){
            return;
        }
        
        inOrderQueue(root->left, queue);
        queue.push(root);
        inOrderQueue(root->right, queue);
    }
public:
    TreeNode* convert(TreeNode* root) {
        std::queue<TreeNode *> queue;
        inOrderQueue(root, queue);
        if(queue.empty()){
            return root;
        }
        
        root = queue.front(); queue.pop();
        TreeNode *prev = root, *curr = nullptr;
        prev->left = nullptr;
        while (!queue.empty()){
            curr = queue.front(); queue.pop();
            prev->right = curr;
            curr->left = prev;
            prev = curr;
        }
        prev->right = nullptr;
        return root;
    }
};

时间复杂度O(N)，额外空间复杂度为O(N)

递归实现

思路

（1）定义递归函数process。

其功能是：

• 将一颗二叉搜索树转换为一个结构有点特殊的有序双向队列，并返回这个链表的尾节点。结构特殊是指这个双向链表尾节点的right指针指向该双向链表的头结点。
• 简单来说，就是将一颗二叉搜索树转换为有序的双向链表，然后让最大值节点的right指向最小值节点，最后返回最大值节点

举例子：

• 搜索二叉树只有一个节点时（最终返回节点1）：
  
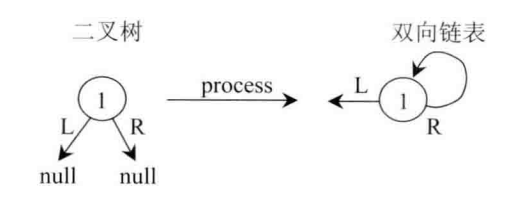
• 一般情况，如下（返回节点3）

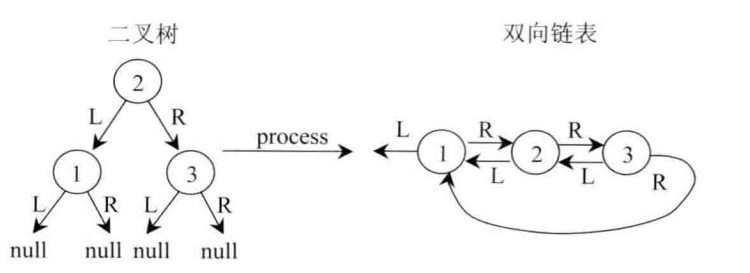
（2）实现process。

假设二叉搜索树如下：

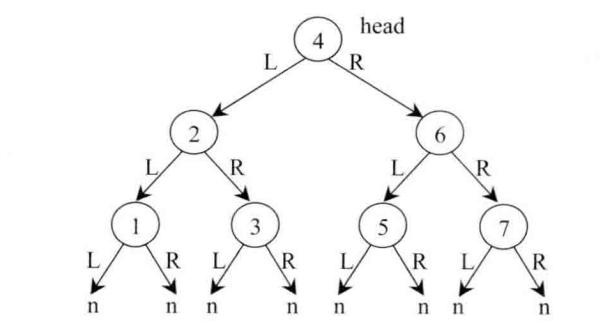
我们先处理左子树，再处理右子树，最终如下：

之后在处理成下面：

然后将尾节点的right指针设为null

class Solution {
    TreeNode* process(TreeNode* root){
        if(root == nullptr){
            return nullptr;
        }


        TreeNode *leftE = process(root->left);
        TreeNode *rightE = process(root->right);
        TreeNode *leftS = leftE != nullptr ? leftE->right : nullptr;
        TreeNode *rightS = rightE != nullptr ? rightE->right : nullptr;
        if(leftE != nullptr && rightE != nullptr){
            leftE->right = root;
            root->left = leftE;
            root->right = rightS;
            rightS->left = root;
            rightE->right = leftS;
            return rightE;
        }else if(leftE != nullptr){
            leftE->right = root;
            root->left = leftE;
            root->right = leftS;
            return root;
        }else if(rightE != nullptr){
            root->right = rightS;
            rightS->left = root;
            rightE->right = root;
            return rightE;
        }else{
            root->right = root;
            return root;
        }
    }
public:
    TreeNode* convert(TreeNode* root) {
        if(root == nullptr){
            return nullptr;
        }
        
        TreeNode *last = process(root);
        root = last->right;
        last->right = nullptr;
        return root;
    }
};

时间复杂度为O(N)，空间复杂度为O(h)，h为二叉树的高度