leetcode：463. 岛屿的周长_leetcode岛屿周长-优快云博客

题目来源

leetcode

题目描述

在这里插入图片描述

题目解析

模拟

class Solution {
    constexpr  static  int dx[4] = {0, 1, 0, -1};
    constexpr static  int dy[4] = {1, 0, -1, 0};

public:
    int islandPerimeter(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if(grid[i][j]){
                    int cnt = 0;
                    for (int k = 0; k < 4; ++k) {
                        int tx = i + dx[k], ty = i + dy[k];
                        if(tx < 0 || tx >= n || ty < 0 || ty >= m || !grid[tx][ty]){
                            cnt += 1;
                        }
                    }
                    ans += cnt;
                }
            }
        }
        return ans;
    }
};

DFS

岛屿问题是一类经典的网格搜索类问题。要求解这道题，我们首先来看如何在网格上做 DFS，再看如何在 DFS 的时候求岛屿的周长。

如何在网格上做DFS

网格问题是这样一类搜索问题：有m * n个小方格，组成一个网格，每个小方格与其上下左右四个方格认为是相邻的，在在这样的网格上进行某种搜索，请尽量用DFS来写代码。

下面我们一步步地构造出方格类 DFS 的代码。

void dfs(vector<vector<int>>& grid, int r, int c){
    dfs(grid, r - 1, c); // 上边相邻
    dfs(grid, r + 1, c); // 下边相邻
    dfs(grid, r, c - 1); // 左边相邻
    dfs(grid, r, c + 1); // 右边相邻
}

但是，对于网格边缘的方格，上下左右并不都有邻居。一种做法是在递归调用之前判断方格的位置，例如位于左边缘，则不访问其左邻居。但这样一个个判断写起来比较麻烦，我们可以用“先污染后治理”的方法，先做递归调用，再在每个DFS函数的开头判断坐标是否合法，不合法的直接返回。同样的，我们还需要判断该方格是否有岛屿（值是否为1），否则也需要返回

void dfs(vector<vector<int>>& grid, int r, int c){
    // 若坐标不合法，直接返回
    if(!(r >= 0 && r < grid.size() && c >= 0 && c < grid[r].size())){
        return;
    }

    // 若该方格不是岛屿，直接返回
    if(grid[r][c] != 1){
        return;
    }
    dfs(grid, r - 1, c); // 上边相邻
    dfs(grid, r + 1, c); // 下边相邻
    dfs(grid, r, c - 1); // 左边相邻
    dfs(grid, r, c + 1); // 右边相邻
}

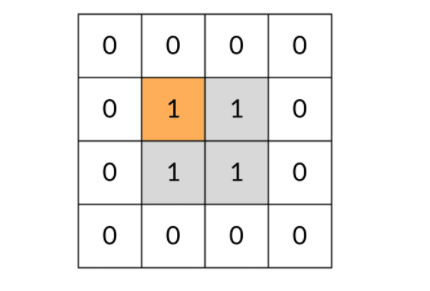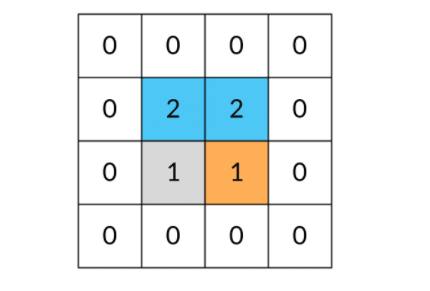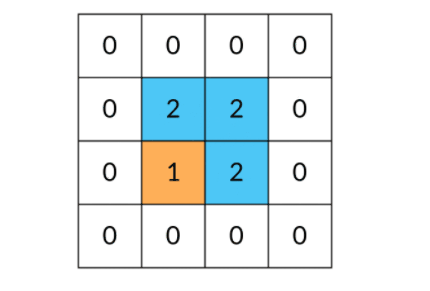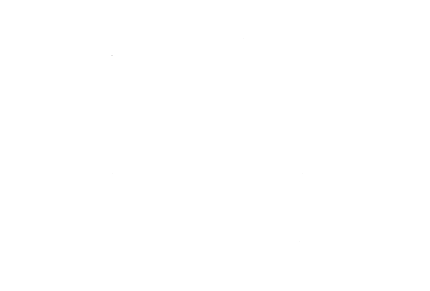
是这样还有一个问题：DFS 可能会不停地“兜圈子”，永远停不下来，如下图所示：
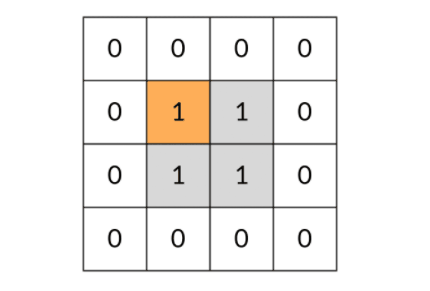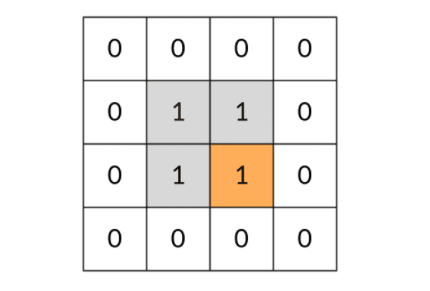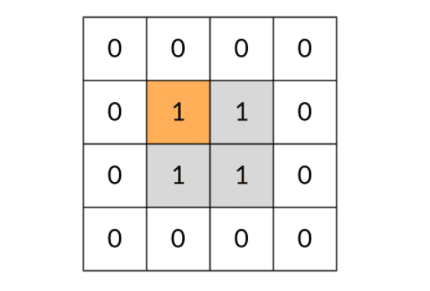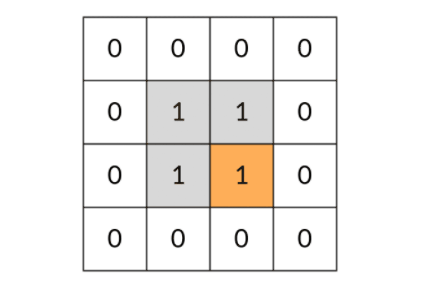
请添加图片描述
因此，我们需要标记遍历过的方格，保证方格不进行重复遍历。标记遍历过的方格并不需要使用额外的空间，只需要改变方格中存储的值就可以。在这道题中，值为 0 表示非岛屿（不可遍历），值为 1 表示岛屿（可遍历），我们用 2 表示已遍历过的岛屿。
请添加图片描述

void dfs(vector<vector<int>>& grid, int r, int c){
    // 若坐标不合法，直接返回
    if(!(r >= 0 && r < grid.size() && c >= 0 && c < grid[r].size())){
        return;
    }

    // 已遍历过（值为2）的岛屿在这里会直接返回，不会重复遍历
    if(grid[r][c] != 1){
        return;
    }
    grid[r][c] = 2; // 将方格标记为"已遍历"
    dfs(grid, r - 1, c); // 上边相邻
    dfs(grid, r + 1, c); // 下边相邻
    dfs(grid, r, c - 1); // 左边相邻
    dfs(grid, r, c + 1); // 右边相邻
}

如何在DFS遍历时求岛屿的周长

求岛屿的周长其实有很多种方法，如果用 DFS 遍历来求的话，有一种很简单的思路：岛屿的周长就是岛屿方格和非岛屿方格相邻的边的数量。注意，这里的非岛屿方格，既包括水域方格，也包括网格的边界。我们可以画一张图，看得更清晰：

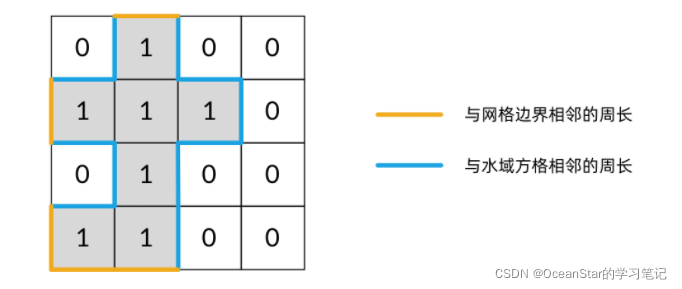
在这里插入图片描述
将这个“相邻关系”对应到 DFS 遍历中，就是：每当在 DFS 遍历中，从一个岛屿方格走向一个非岛屿方格，就将周长加 1。代码如下：


int dfs(vector<vector<int>>& grid, int r, int c){
    // 从一个岛屿方格走向网格边界，周长加 1
    if(!(r >= 0 && r < grid.size() && c >= 0 && c < grid[r].size())){
        return 1;
    }

    // 从一个岛屿方格走向水域方格，周长加 1
    if (grid[r][c] == 0) {
        return 1;
    }


    if (grid[r][c] != 1) {
        return 0;
    }
    grid[r][c] = 2;
    return dfs(grid, r - 1, c)
           + dfs(grid, r + 1, c)
           + dfs(grid, r, c - 1)
           + dfs(grid, r, c + 1);
}

完整代码如下：

int dfs(vector<vector<int>>& grid, int r, int c){
    if(!(r >= 0 && r < grid.size() && c >= 0 && c < grid[c].size())){
        return 1;   // 从一个岛屿方格走向网格边界，周长加 1
    }

    if(grid[r][c] == 0){
        return 1;   // 从一个岛屿方格走向水域方格，周长加 1
    }

    if(grid[r][c] == 2){
        return 0;  // 之前访问过，直接返回，返回0，无周长收益
    }

    grid[r][c] = 2;
    return dfs(grid, r - 1, c) + dfs(grid, r + 1, c)
         + dfs(grid, r, c - 1) + dfs(grid, r, c + 1);
}

int islandPerimeter(vector<vector<int>>& grid) {
    for (int i = 0; i < grid.size(); ++i) {
        for (int j = 0; j < grid[i].size(); ++j) {
            if(grid[i][j]){
                // 题目限制只有一个岛屿，计算一个即可
                return dfs(grid, i, j);
            }
        }
    }

    return 0;
}

我们对于每个格子的四条边分别来处理，首先看左边的边，只有当左边的边处于第一个位置或者当前格子的左面没有岛格子的时候，左边的边计入周长。其他三条边的分析情况都跟左边的边相似

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        int m = grid.size(), n = grid[0].size(), res = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) continue;
                if (j == 0 || grid[i][j - 1] == 0) ++res;
                if (i == 0 || grid[i - 1][j] == 0) ++res;
                if (j == n - 1 || grid[i][j + 1] == 0) ++res;
                if (i == m - 1 || grid[i + 1][j] == 0) ++res;
            }
        }
        return res;
    }
};

下面这种方法对于每个岛屿格子先默认加上四条边，然后检查其左面和上面是否有岛屿格子，有的话分别减去两条边，这样也能得到正确的结果，参见代码如下：

class Solution {
public:
    int islandPerimeter(vector<vector<int>>& grid) {
        if (grid.empty() || grid[0].empty()) return 0;
        int res = 0, m = grid.size(), n = grid[0].size();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] == 0) continue;
                res += 4;
                if (i > 0 && grid[i - 1][j] == 1) res -= 2;
                if (j > 0 && grid[i][j - 1] == 1) res -= 2;
            }
        }
        return res;
    }
};