二叉树的直径

继续打卡每日一题，今天给大家带来一道二叉树类型的题目

题目描述：

给你一棵二叉树的根节点，返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。

题目示例：

这道题目虽然官方说是简单题，但是难度绝对是属于中等，其难度不在于书写难度，而在于题目的理解成本

针对树类型的题目，大家一定要对前中后序遍历以及层次遍历烂熟于心，虽然大家也看到很多官方解答一直提到BFS（广度优先）、DFS（深度优先），但是这两种遍历也是属于上面的几种遍历

• BFS就是层次遍历
• DFS的表现形式就是前中后序遍历的任意一种

具体的遍历逻辑很简单，

    private void visit(TreeNode node) {
        if (node == null) {
            return;
        }
        //前序
        //执行相关逻辑
        visit(node.left);
        visit(node.right);
    }

中序和后序只需调整执行逻辑的位置即可

中序

      visit(node.left);
      //执行相关逻辑
        visit(node.right);

后序

      visit(node.left);
       visit(node.right);
        //执行相关逻辑

现在回到我们的题目，以下面的case为例：

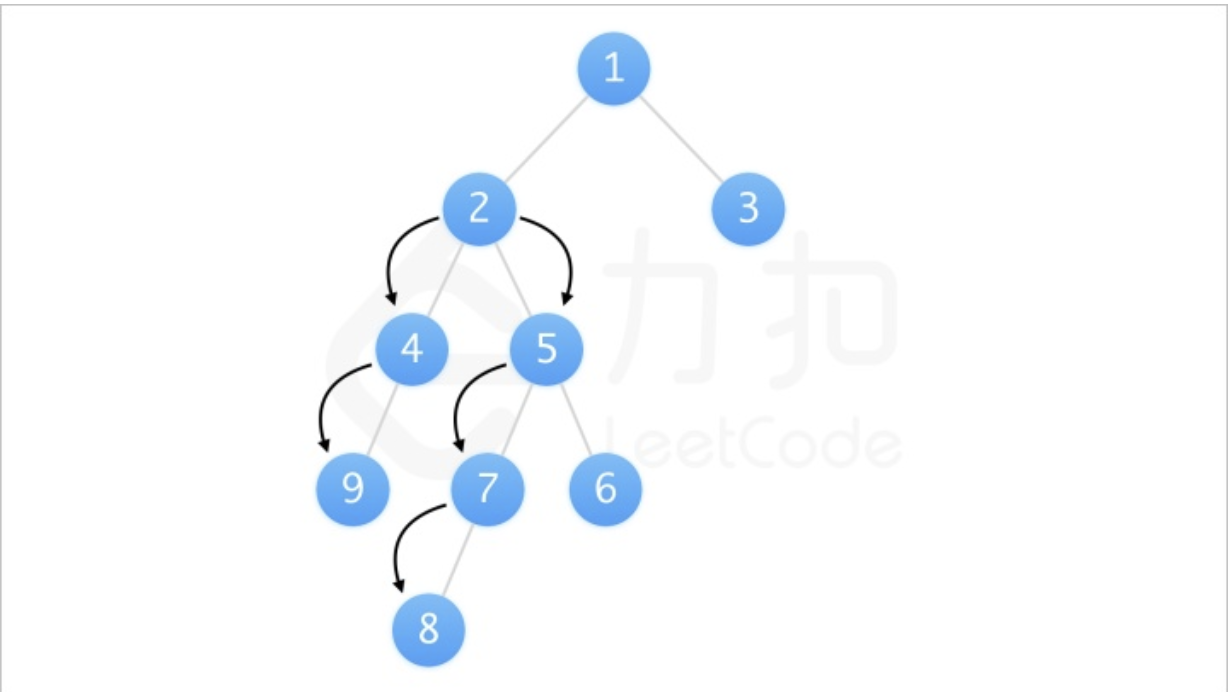
如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 2 为起点，从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。

所经历的节点：4，9，5，7，8 和当前根节点：2，其中

• 4，9为左子树的最大节点数
• 5，7，8为右子树的最大节点数

现在我们推广到一般的场景：

假设我们知道对于该节点的左子树向下遍历经过最多的节点数 L （即以左儿子为根的子树的深度）

和其右儿子向下遍历经过最多的节点数 R （即以右儿子为根的子树的深度）

那么以该节点为起点的路径经过节点数的最大值即为 L+R+1 。

其中1是当前根节点

那么边数=节点数-1=(L+R+1)-1=L+R

所以题目中的问题其实就是找从A点->B点，使A->B经历的节点数最多，找到最大节点数之后，减1就是我们的最大边数，即树的直径

下面问题又变为如何去找最多的节点数的问题，对于树的遍历，无非我上面提到的几种方式（前中后，层次），但是本题需要计算左子树的节点和右子树的节点数，然后进行相加，所以后序遍历最为合适

• 核心代码

  private int visit(TreeNode node) {
        if (node == null) {
            //空节点
            return 0;
        }
        int LNodeNums = visit(node.left);
        int RNodeNums = visit(node.right);
        int currentNodeNums = LNodeNums + RNodeNums + 1;
        maxNodes = Math.max(currentNodeNums, maxNodes);
        //返回最大的节点数
        return Math.max(LNodeNums, RNodeNums) + 1;
    }

完整代码：

public class 二叉树的直径 {
    int maxNodes;

    public int diameterOfBinaryTree(TreeNode root) {
        maxNodes = 1;
        visit(root);
        //边数=节点数-1
        return maxNodes - 1;
    }

    private int visit(TreeNode node) {
        if (node == null) {
            //空节点
            return 0;
        }
        int LNodeNums = visit(node.left);
        int RNodeNums = visit(node.right);
        int currentNodeNums = LNodeNums + RNodeNums + 1;
        maxNodes = Math.max(currentNodeNums, maxNodes);
        //返回最大的节点数
        return Math.max(LNodeNums, RNodeNums) + 1;
    }
}