最短路径问题是图论研究中的一个经典算法问题, 旨在寻找图(由结点和路径组成的)中两结点之间的最短路径。
Dijkstra算法:
Dijkstra算法(迪杰斯特拉)是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。 迪杰斯特拉(Dijkstra)算法是典型最短路径算法,用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想),直到扩展到终点为止。
代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <stack>
#include <string>
using namespace std;
//顶点的最大值
const int MAX_NUM = 100;
//距离的最大值
const int MAX_POLICY = 1e7;
//矩阵
int map[MAX_NUM][MAX_NUM];
//源点到各个顶点的最短数组
int dist[MAX_NUM];
int p[MAX_NUM];
//顶点个数和边的个数
int n, m;
//是否加入集合S,如果在集合S里面的话,值为true,否则在集合S-V里面,值为false;
bool flag[MAX_NUM];
//Dijkstra算法
void dijkstra(int start)
{
for (int i = 1; i <= n; ++i)
{
flag[i] = false;
dist[i] = map[start][i];
if (dist[i] != MAX_POLICY)
{
//dist[i] = map[start][i];
p[i] = start;
}
else
{
p[i] = -1;
}
}
flag[start] = true;
dist[start] = 0;
for (int i = 1; i <= n; ++i)
{
int min_dist = MAX_POLICY, t = start;
for (int j = 1; j <= n; j++)
{
if (dist[j] < min_dist && !flag[j])
{
min_dist = dist[j];
t = j;
}
}
if (t == start) return;
flag[t] = true;
for (int j = 1; j <= n; j++)
{
if (map[t][j] < MAX_POLICY && !flag[j])
{
if (dist[j] > (dist[t] + map[t][j]))
{
dist[j] = dist[t] + map[t][j];
p[j] = t;
}
}
}
}
}
void showProcess(int start)
{
int value;
stack<int> stack;
for (int i = 1; i <= n; ++i)
{
value = p[i];
cout << "源点" << start << "到" << i << "的路径是";
while (value != -1)
{
stack.push(value);
value = p[value];
}
while (!stack.empty())
{
//pop函数是出来栈,没有返回值,先取出栈顶值,然后出栈
int node = stack.top();
stack.pop();
std::cout << node << "-";
}
cout << i << "最短距离为" << dist[i] << endl;
}
}
void input_output() {
//顶点u到顶点v的权重是w, 然后输入的起始地点是start;
int u, v, w, start;
cout << "请输入顶点个数" << endl;
cin >> n;
if (n <= 0)
{
cout << "输入的顶点个数因该大于0!" << endl;
return;
}
cout << "请输入边的个数" << endl;
cin >> m;
if (m <= 0)
{
cout << "输入的边的个数不能小于0" << endl;
return;
}
//邻接矩阵的初始化,默认都为最大值,注意这里下标都是从1开始
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= n; ++j)
{
map[i][j] = MAX_POLICY;
}
}
for (int i = 0; i < m; ++i)
{
cout << "请输入" << (i + 1) << "条边的两个顶点及其距离" << endl;
cin >> u >> v >> w;
if (u > n || v > n)
cout << "您输入的顶点有误" << endl;
//如果2次输入一样顶点,那么取最小的
map[u][v] = min(map[u][v], w);
}
cout << "请输入起始的位置" << endl;
cin >> start;
if (start < 0 || start > n)
{
cout << "输入的起始顶点有误" << endl;
return;
}
dijkstra(start);
cout << "你所在的位置 " << start << endl;
for (int i = 1; i <= n; ++i)
{
cout << "你" << start << ")要去的位置是" << i;
if (dist[i] == MAX_POLICY)
cout << "无路可到" << endl;
else
cout << "最短距离为" << dist[i] << endl;
}
showProcess(start);
while (true) {
int p = 0;
cout << "*********************" << endl;
cout << "*******1、在此基础上重新输入起始位置*******" << endl;
cout << "*******0、退出,重新开始*******" << endl;
cout << "*********************" << endl;
cout << "请输入数字:" << endl;
int number;
cin >> number;
switch (number)
{
case 1:
cout << "请输入起始的位置" << endl;
cin >> start;
if (start < 0 || start > n)
{
cout << "输入的起始顶点有误" << endl;
return;
}
dijkstra(start);
cout << "你所在的位置 " << start << endl;
for (int i = 1; i <= n; ++i)
{
cout << "你" << start << ")要去的位置是" << i;
if (dist[i] == MAX_POLICY)
cout << "无路可到" << endl;
else
cout << "最短距离为" << dist[i] << endl;
}
showProcess(start);
break;
case 0:
p = 1;
break;
default:
cout << "输入有误,请重新输入!" << endl;
break;
}
if (p == 1) {
break;
}
}
}
int main()
{
while (true) {
cout << "*********************" << endl;
cout<< "*******1、开始程序*******" << endl;
cout << "*******0、退出程序*******" << endl;
cout << "*********************" << endl;
cout << "请输入数字:" << endl;
int number;
cin >> number;
switch (number)
{
case 1:
input_output();
break;
case 0:
system("pause");
return 0;
default:
break;
}
}
system("pause");
return 0;
}
运行结果:
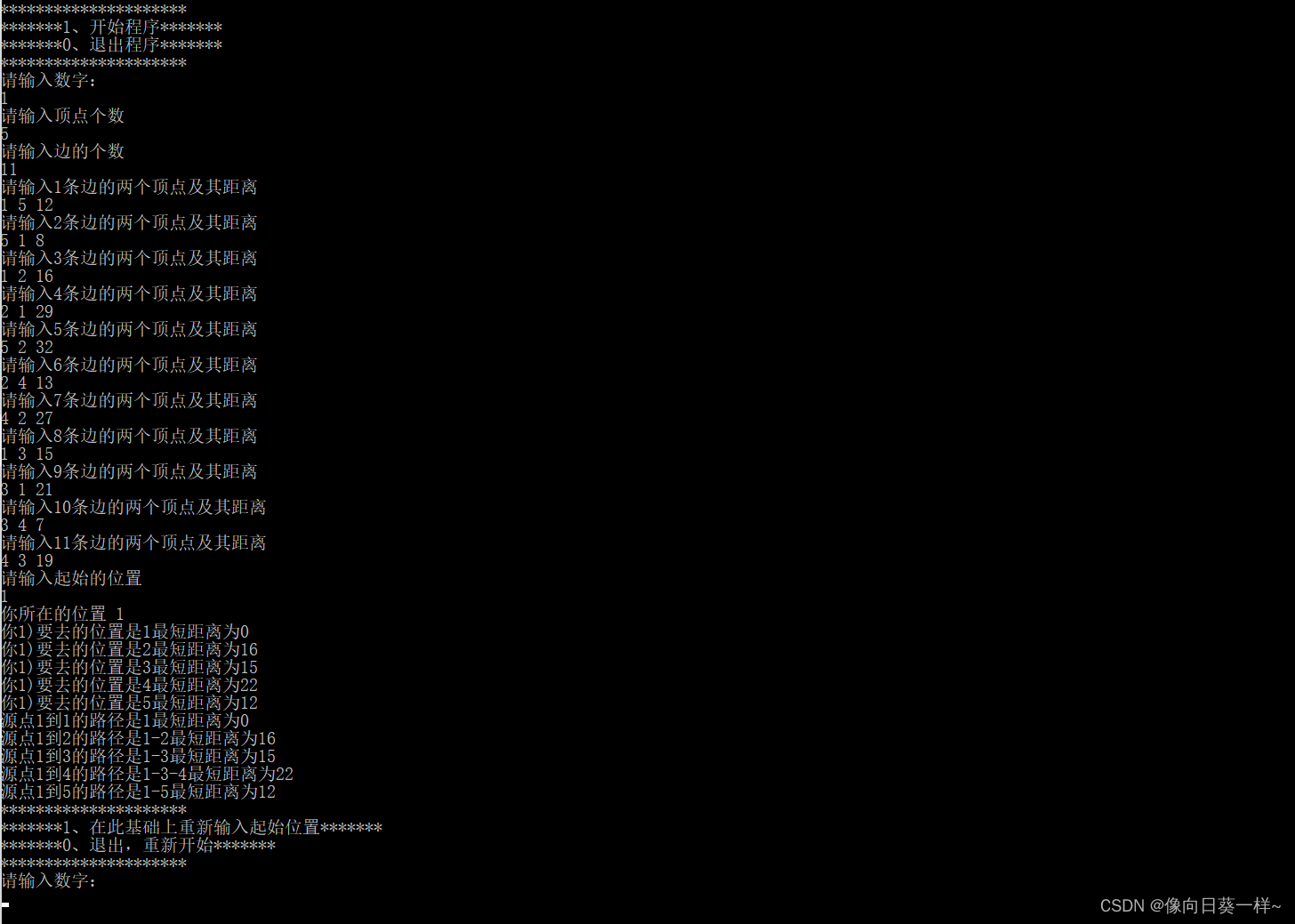
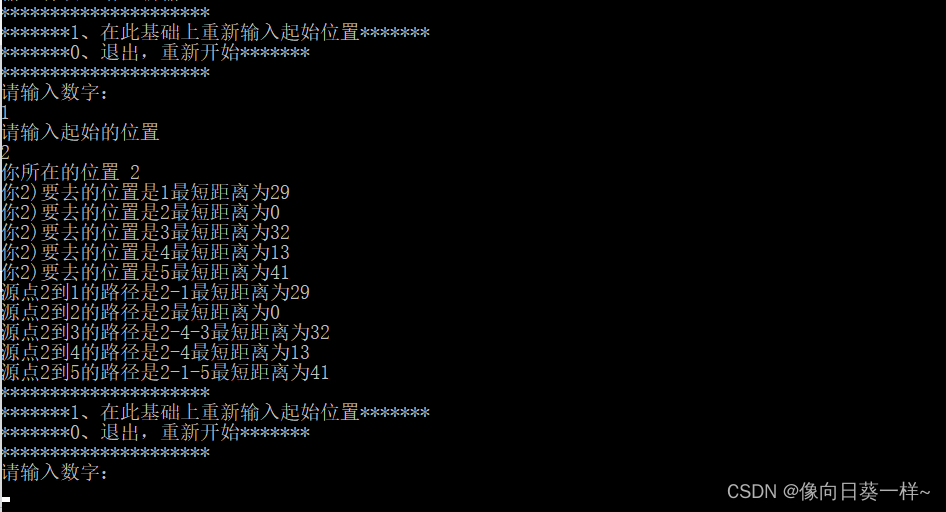





 本文详细介绍了Dijkstra算法,包括其原理、特点,并提供了一个C++代码示例。通过实例演示了如何计算图中两点之间的最短路径,以及如何进行路径展示。适合理解图论和寻找最短路径问题的开发者使用。
本文详细介绍了Dijkstra算法,包括其原理、特点,并提供了一个C++代码示例。通过实例演示了如何计算图中两点之间的最短路径,以及如何进行路径展示。适合理解图论和寻找最短路径问题的开发者使用。

















 2278
2278

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










