关于图论（very difficult for me）

原创 已于 2024-03-20 13:07:22 修改 · 314 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#图论 #算法

于 2024-03-18 18:00:51 首次发布

   一.图的基本概念

     关于图的分类：

1：无向图

每条边的长度是无方向的，可以理解为数学上的直线，两段都可以进行到这条线的另一端。

2：有向图

每条边都是有方向的，可以理解为数学上的射线，规定了只有从a点到b点的道路，在这条路上，b不可以向a的方向前进。

3.完全图

任意两个点都可以互相到达，在这里会有两种不同的情况。

第一种：完全无向图

因为无向图两端都可以互相到达，所以在完全无向图只需每两个点上都有无向边连接.

第二种：完全有向图

因为有向边有着限定的方向，所以在每两个点之间都要有两条且方向互相相反的有向边相连接

讲完了三种基本的图，接下来就讲讲衍变的图；

子图：

从原来的图中取出一部分来进行集合（有向图和无向图都适用）

带权图：

在图中，每条边都有着数值（有向图和无向图都适用）

连通图：

 在无向图中，任意两个点都有路径可以到达

强连通图：

在有向图中，任意两个点都有路径可以到达。

二：简单的题目练习

 深搜：

按照树的先序遍历。

看一下一道题目，关于深搜和图论的；

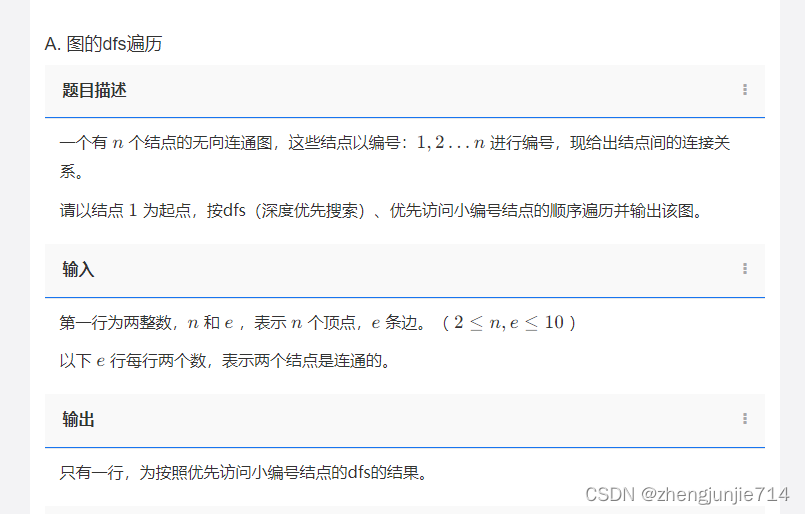
可以看到这是无向图的问题，并且用到了深搜的思想。

我们先来看一下代码啊

#include<bits/stdc++.h>
using namespace std;
int a[20][20];
int n,e;
bool f[20];
void dfs(int x)
{
	f[x]=true;
	cout<<x<<" ";
	for(int i=1;i<=n;i++)
	{
		if(a[x][i]==1&&f[i]==false)
		{
			dfs(i);
		}
	 } 
}
int main(){
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++)
	{
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1; 
	}
	dfs(1);

	
	return 0;
}

可以看到，这里运用了深搜的思想。

而提到了深搜，而就又不得不提起

广搜

这是按照树的层次进行排序的

树在这里就不在多赘述了，我们直接来看一道的题目；


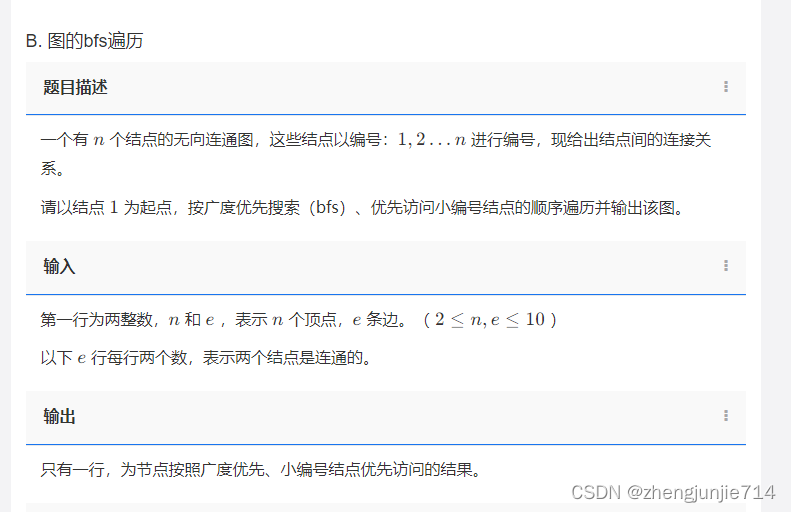
我们直接来看下代码

#include<bits/stdc++.h>
using namespace std;
int a[20][20];
int q[20];
int h,t;
bool f[20];
int n,e;
void dfs(int x)
{
	f[x]=true;
	cout<<x<<" ";
	for(int i=1;i<=n;i++)
	{
		if(a[x][i]==1&&f[i]==false)
		{
			dfs(i);
		}
	 } 
}
int main(){
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++)
	{
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1; 
	}
	h=1;
	t=1;
	q[1]=1;
	f[1]=true;
	cout<<1<<" "
	;while(h<=t)
	{
		for(int i=1;i<=n;i++)
		{
			if(a[q[h]][i]==1&&!f[i])
			{
				cout<<i<<" ";
				t++;
				q[t]=i;
				f[i]=true;
			}
		}
	h++;	
	}


	
	return 0;
}

欧拉路的基本概念

性质：就可以从其中一点出发，不重复地走完其所有边。

欧拉回路

可以一笔从起点到终点且回到起点并走过了所有的边的路叫做欧拉回路

那如何来判断他是否是欧拉回路呢？

首先有一个大前提：就是必须是连通图；

然后再分两种情况；

①无向图，有着偶数个数的寄点；

②有向图，有向图除了重点和起点外，其余的出度和入度相等（起点出度=入度+1，终点入度=出度+1，所以可以出度==入度）

欧拉路的题目

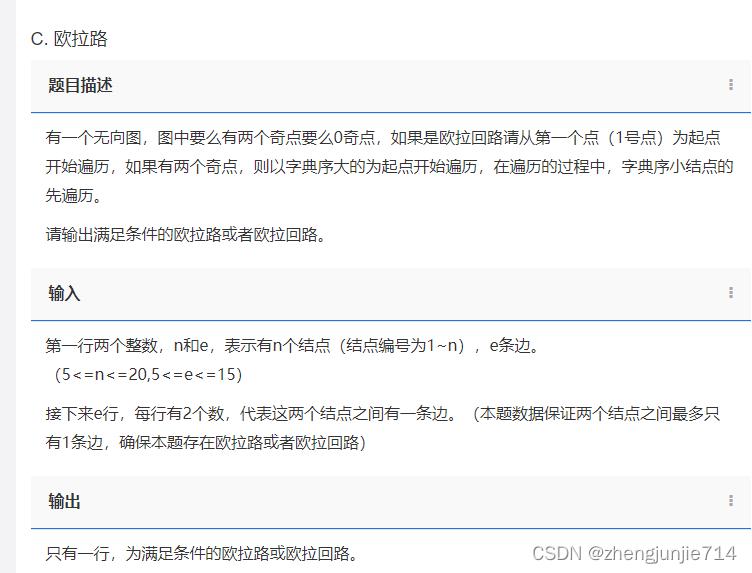
由于前面的概念讲的十分详细，所以这里也不再多说了

#include<bits/stdc++.h>
using namespace std;
int a[30][30];
int n,e;
int d[30];
int r[50];
int k;
void dfs(int x)
{
	for(int i=1;i<=n;i++)
	{
		if(a[x][i]==1)
		{
			a[x][i]=0;
			a[i][x]=0;
			dfs(i);
		}
	}
	k++;
	r[k]=x;
	
	
}
int main(){
	cin>>n>>e;
	for(int i=1;i<=e;i++)
	{
		int x,y;
		cin>>x>>y;
		a[x][y]=1;
		a[y][x]=1;
		d[x]++;
		d[y]++;
	}	
	int s=1;
	for(int i=n;i>=1;i--)
	{
		if(d[i]%2==1)
		{
			s=i;
			break;
		}
	}
	dfs(s);
	for(int i=k;i>=1;i--)
	{
		cout<<r[i]<<" ";
	}
	return 0;
}

三：图论的加深（最短路问题）

前面的地方是撒撒水的啦，但是从现在开始，才可以算是真正通往图论的大门。

1：Dijketra（迪杰斯特拉）算法

在学习每一种问题时，我们都要了解它的基本思想和它的基本算法。而Dijketra算法则就是解决有权图（可以看一下我前面讲义的知识点）中最短路径问题。提到最短，大家脑海中都不自觉地想起——贪心策略！！所以Dijketra也是采用局部最优解的方法来解决最短路径的问题。

同时，它还是典型的单源最短路径算法：从起始点为中心向外层层扩展，直到到达终点位置才停止。

不过，值得一提的是，Dijketra算法只能用于边权为正的图（无向和有向都行），它不可以有负边权的图。

2：Dijketra（迪杰斯特拉）算法的例题讲解

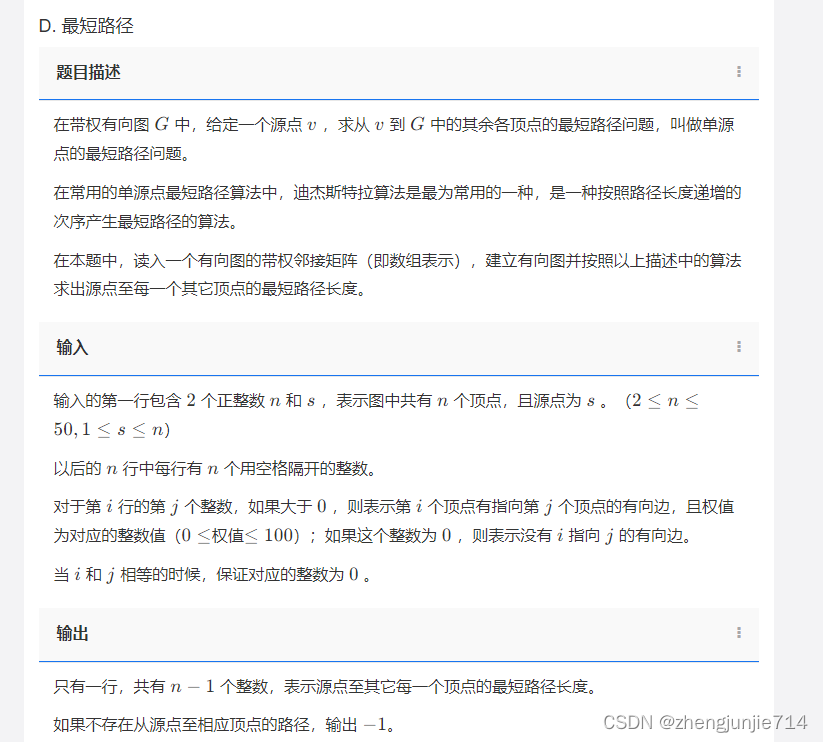
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=60;
int a[N][N];
int d[N];
bool f[N];
int n,s;
int main(){
    cin>>n>>s;
	for(int i=1;i<=n;i++)
	{
  		for(int j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}
	}           	         
    memset(d,0X3f,sizeof(d));
    d[s]=0;
	for(int i=1;i<=n;i++)
	{
		int mi=-1;
		for(int j=1;j<=n;j++)
		{
			if(!f[j] && (mi==-1 || d[j] < d[mi]))
			{
				mi=j;
			}
		}
		f[mi]=true;
		for(int j=1;j<=n;j++)
		{
			if(!f[j] && a[mi][j]!=0 && d[mi]+a[mi][j]<d[j])
			{
				d[j]=d[mi]+a[mi][j];
			}
		}
	}                          	
    for(int i=1;i<=n;i++)
	{
		if(i!=s)
		{
			if(d[i]!=INF)cout<<d[i]<<" ";
			else cout<<-1<<" ";
		}
    }                          	
	
	return 0;
}

  我们就借用这道题的题目和答案进行一个分析。

首先，在定义数组的时候，我定义了一个最大值，有些人就会疑惑，为啥不用INT_MAX呢？因为在图论的求解过程中，很可能会在权边的之中进行加法，但INT_MAX加上任何的数的时候会溢出出，所以要用0x3f3f3f3f，这个数字，至于为什么，因为这个数就算加上自己，也不会超过int，所以在初始化组a时，可以使用memset初始化函数，使用方法看我上面的代码，而剩下的部分，就是运用贪心算法进行编写了，在这提一嘴，记住贪心是局部最优解，动态规划是全局最优解。

3.Dijketra（迪杰斯特拉）算法的常见题目

在这里，我不会重复的把每个知识点讲多次，我只会讲每到题的特殊之处

先做事再递归与先递归再做事。

这两个的做事情顺序是截然相反的！在写题目的时候一定要分的清它写的代码是什么顺序。否则就只会全局崩盘，我们来看一下题目

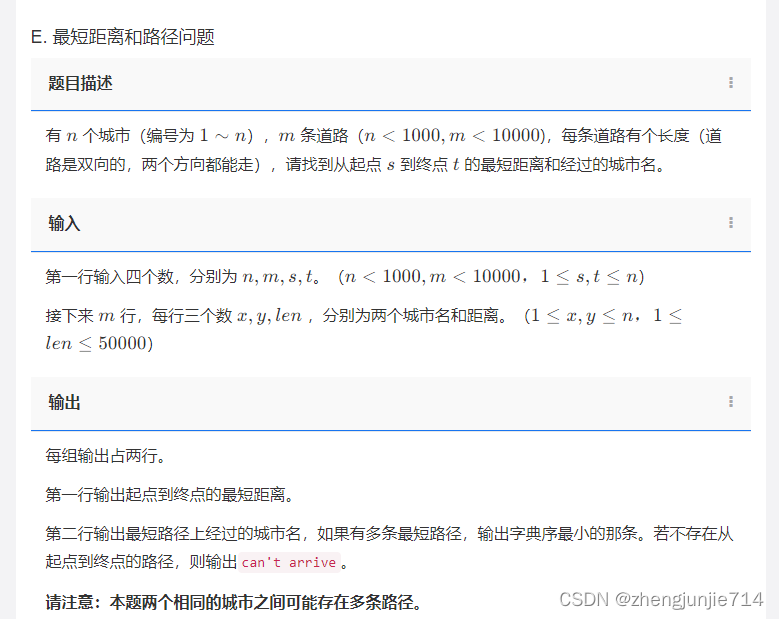
，可以从题目中所表达的意思中明白，这是先递归再做事。

我们来看一下代码。

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1010;
int a[N][N];
int d[N];
bool f[N];
int r[N];
int n,m,s,t;
int len,x,y;
void print(int k)
{
	if(r[k]!=0)
	{
		print(r[k]);
	}
	cout<<k<<" ";
}
int main(){
	cin>>n>>m>>s>>t;
	
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y>>len;
		if(a[x][y]==0||len<a[x][y])
		{
			a[x][y]=len;
			a[y][x]=len;	
		}	
	}
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	for(int i=1;i<=n;i++)
	{
		int mi=-1;
		for(int j=1;j<=n;j++)
		{
			if(!f[j] && (mi==-1 || d[j] < d[mi]))
			{
				mi=j;
			}
		}
		f[mi]=true;
		for(int j=1;j<=n;j++)
		{
			if(!f[j] && a[mi][j]!=0 && d[mi]+a[mi][j]<d[j])
			{
				d[j]=d[mi]+a[mi][j];
				r[j]=mi;
			}
		}
	}  
	if(d[t]!=INF)
	{
		cout<<d[t]<<endl;	
		print(t);
	}
	else cout<<"can't arrive";
	return 0;
}

4.邻接表的存储和遍历

在这里，用数组模拟的方法，而我们用一个专有名词来形容它，叫做链式前向星。

链式向前星

链式向前星与前面的邻接矩阵有什么不同呢？我们分别从它的存储方法和适用题型来进行分来啊。

①链式前向星是按照边来进行存图，所以邻接表是来存储稀疏图。

②相反地，邻接矩阵来按照点来存图，且适合用于稠密图。

了解了基本的知识，我们来

链式向前星的题目练习

#include<bits/stdc++.h>
using namespace std;
struct edge{
	int from,to,next;
};
edge a[10010];
int pre[1000100];
int n,e;
int k=0;
void add(int u,int v)
{
	k++;
	a[k].from=u;
	a[k].to=v;
	a[k].next=pre[u];
	pre[u]=k;
}
struct node{
	int x,y;
}; 
node p[10010];
bool cmp(node n1,node n2)
{
	return n1.x<n2.x||(n1.x==n2.x&&n1.y>n2.y)
;}
int main(){
	int n,e;
	cin>>n>>e;
	int x,y;
	for(int i=1;i<=e;i++)
	{
		cin>>p[i].x>>p[i].y;
	}
	sort(p+1,p+e+1,cmp);
	for(int i=1;i<=e;i++)
	{
		add(p[i].x,p[i].y);
	}
	for(int i=1;i<=n;i++)
	{
		if(pre[i]==0)continue;
		cout<<i<<endl;
		for(int j=pre[i];j!=0;j=a[j].next)
		{
			cout<<a[j].to<<" ";
		}
		
		cout<<endl;
	}

	return 0;
} 

#include<bits/stdc++.h>
using namespace std;
struct edge{
	int from,to,len,next;
};
edge a[100];
int pre[20];
int s,t;
int k=0;
const int INF=0x3f3f3f3f;
int d[20];
bool f[20];
int n,e;
void add(int u,int v,int l)
{
	k++;
	a[k].from=u;
	a[k].to=v;
	a[k].len=l;
	a[k].next=pre[u];
	pre[u]=k;
}
void dijkstra(){
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	for(int i=1;i<=n;i++)
	{
		int mi=-1;
		for(int j=1;j<=n;j++)
		{
			if(!f[j]&&(mi==-1||d[j]<d[mi]))
			{
				mi=j;
			}
		}
		f[mi]=true;
		for(int j=pre[mi];j!=0;j=a[j].next){
			int to=a[j].to;
			if(!f[to]&&d[mi]+a[j].len<d[to])
			{
				d[to]=d[mi]+a[j].len;
			}
		}
	}
}
int main(){
	cin>>n>>e;
	int x,y,l;
	for(int i=1;i<=e;i++)
	{
		cin>>x>>y>>l;
		add(x,y,l);
		add(y,x,l);
	}
	cin>>s>>t;
	dijkstra();
	if(d[t]!=INF)cout<<d[t];
	else cout<<"No path";

	return 0;
}

现在我们来讲讲最后一个知识点（终于！！）--SPFA求最短路径

1.SPFA的基本知识

那这个知识点有什么特殊之处呢？？它使用于负权边的问题，它与bfs（广度优先搜素）十分的相似，它们唯一的不同是shortest Path Faster Algorithm(也就是SPFA的全称)是可以将一个点重复的取除或放回队列，用来对其它的点来进行一个改造，直到最优点的出现，而bfs则出了队列就不可以重新进去队列了。

2.SPFA的题目

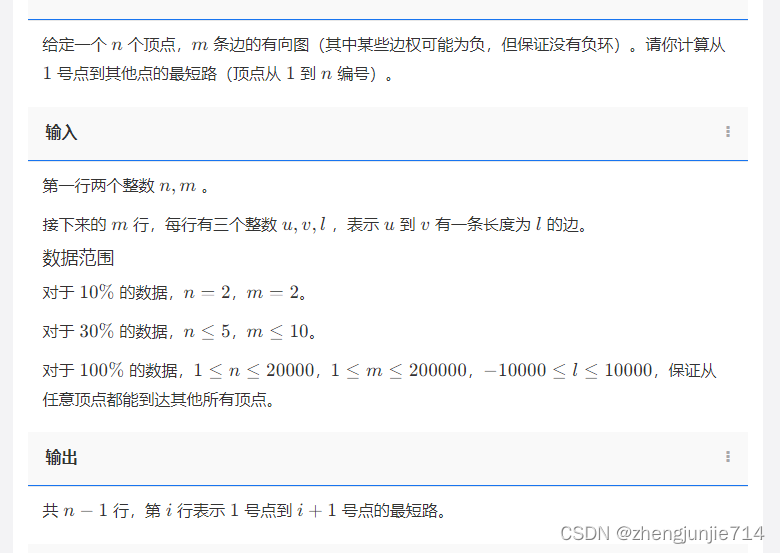
#include<bits/stdc++.h>
using namespace std;
struct edge{
	int from,to,len,next;
};
edge a[200010];
int pre[20010];
int s,t;
queue<int> q;
bool f[20010];
int k=0;
int d[20010];
const int INF=0x3f3f3f3f;
int n,e;
void add(int u,int v,int l)
{
	k++;
	a[k].from=u;
	a[k].to=v;
	a[k].len=l;
	a[k].next=pre[u];
	pre[u]=k;
}
void dijkstra(){
	memset(d,0x3f,sizeof(d));
	d[s]=0;
	for(int i=1;i<=n;i++)
	{
		int mi=-1;
		for(int j=1;j<=n;j++)
		{
			if(!f[j]&&(mi==-1||d[j]<d[mi]))
			{
				mi=j;
			}
		}
		f[mi]=true;
		for(int j=pre[mi];j!=0;j=a[j].next){
			int to=a[j].to;
			if(!f[to]&&d[mi]+a[j].len<d[to])
			{
				d[to]=d[mi]+a[j].len;
			}
		}
	}
}
int main(){
	cin>>n>>e;
	int x,y,l;
	for(int i=1;i<=e;i++)
	{
		cin>>x>>y>>l;
		add(x,y,l);
	}
	memset(d,0x3f,sizeof(d));
	d[1]=0;
	q.push(1);
	f[1]=true;
	while(!q.empty())
	{
		int u=q.front();
		for(int i=pre[u];i!=0;i=a[i].next)
		{
			int v=a[i].to;
			if(d[u]+a[i].len<d[v])
			{
				d[v]=d[u]+a[i].len;
				if(!f[v])
				{
					q.push(v);
					f[v]=true;
				}
			}
		}
		q.pop();
		f[u]=false;
	}
	for(int i=2;i<=n;i++)
	{
		cout<<d[i]<<endl;
	}


	return 0;
}

四......

OK呀，这篇文章也是结束了，为了犒劳犒劳我的双手，请献上你的点赞吧

zhengjunjie714
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值