【自己动手写机器学习算法】第5章 决策树

第5章 决策树

顾名思义,"决策树"就是按照建立分支来进行决策的方法,即根据啥(往往是根据某个属性的某个值作为指标，比如“年龄大于20岁的”或“身高大于1米5的”)来区分不同类别的数据,也是一种监督式机器学习算法,从编程角度来看,可以看作是一系列的"if… then… else…"的集合,这个模型非常直观,也即可读性非常好,决策树的学习通常包含三个步骤:特征选择,决策树生成,决策树的剪枝.
给定数据集

D={(x1,y1),(x2,y2),...,(xN,yN)}D = \{ (x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}D={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}
其中,$x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)}{)}^T$为输入实例(特征向量),$n$为特征的个数,yi∈{1,2,...,K}y_i \in \{1,2,...,K\}yi​∈{1,2,...,K}为类别标记,$i=1,2,...,N$,$N$为样本容量

目标

构建决策树,使之能改对大量的实例进行正确分类（而为什么要引入决策树的剪枝呢？是要让这颗树尽可能地好，那什么叫好呢？就是用尽可能少的分叉来高效地区分更多的数据）
(本质是构建一组规则,这组规则可以对每个特征进行划分,但是又不能划分太好,不然容易过拟合,泛化能力就会变差)

5.1数据集

首先建立课本上的数据集合本身

F0:年龄：定义"青年|中年|老年"分别为"1|2|3",
F1:是否有工作：定义"是|否"为"1|2",
F2:有自己的房子：定义"是|否"为"1|2",
F3:信贷情况：“一般|好|非常好"为"1|2|3”,
类别：“是|否"为"1|2”

import numpy as np
x = np.asarray([[1,2,2,1],[1,2,2,2],[1,1,2,2],[1,1,1,1],[1,2,2,1],
               [2,2,2,1],[2,2,2,2],[2,1,1,2],[2,2,1,3],[2,2,1,3],
               [3,2,1,3],[3,2,1,2],[3,1,2,2],[3,1,2,3],[3,2,2,1]])
y = np.asarray([2,2,1,1,2,2,2,1,1,1,1,1,1,1,2])
import pandas as pd

df = pd.concat([pd.DataFrame(x,columns=[u'年龄',u'是否有工作',u'有自己的房子',u'信贷情况']),pd.DataFrame(y,columns=[u'类别'])],axis=1)
df

	年龄	是否有工作	有自己的房子	信贷情况	类别
0	1	2	2	1	2
1	1	2	2	2	2
2	1	1	2	2	1
3	1	1	1	1	1
4	1	2	2	1	2
5	2	2	2	1	2
6	2	2	2	2	2
7	2	1	1	2	1
8	2	2	1	3	1
9	2	2	1	3	1
10	3	2	1	3	1
11	3	2	1	2	1
12	3	1	2	2	1
13	3	1	2	3	1
14	3	2	2	1	2

此时某些用心的读者也许还会发现,给了这些数据之后,实际可以尝试性地按照x的某一列属性作为指标,给定阈值,阈值之上的为某个列别标签,阈值之下的为另一个类别标签,但是问题来啦:选择哪个属性最好呢?
这里不得不说到"信息增益"的问题了,这个东西可以指导模型选择最合适的属性对原始数据进行第一阶的划分.

这里需要对“信息增益”进行一些讲解，信息增益可以这么理解：如果对一件事进行描述，并且需要10次才能描述完整，那么实际每次描述的时候，描述所涵盖的信息量是不相同的，信息增益，就可以理解为一次描述过程的量。对于这里的决策树来说，就是每次if和else所能带有的信息。实际的定义和形式化描述如下：

---

5.2信息熵和信息增益

5.2.1信息熵，经验熵，相对熵

（1）＂熵＂的定义：$$H(X)=-\sum _{i=1}^n{P}_i\log P_i$$

观察上式可以得知，熵只和数据分布有关，所以，$H(X)$可以直接写作$H(p)$，且从定义可以验证
$$0\le H(p)\le \log n$$
（关于＂熵＂为什么要这么定义，这里给一下思路提示：比如，如果要定义一个三位数，实际只用３个字符存储空间就可以了，这也就是为什么取log的原因了，实际表示的是描述某个对象所需要的基本元素的个数，更详细的关于信息论的定义可以自行学习香浓的那一套信息理论，这里我也不懂很多，只给点提示，另外，这里结合课本给出求解信息熵的代码）

from collections import Counter #计数插件
def cal_entropy(x,i):
    """
    计算熵值
    x：数据集
    ｉ：第ｉ个特征
    """
    if x.ndim == 1:
        x = x.reshape((len(x),1)) # 如果是一维的，那么定义为(len(x)行1列)的数据分布
    col_i_data = x[:,i] # 第ｉ列数据
    uniquevalue = np.unique(col_i_data) # 该属性下查找所有可能的值
    H_X = 0 # 统计熵的加和
    for j in range(len(uniquevalue)): 
        i_p = Counter(col_i_data)[j+1]/len(col_i_data) # 对每个属性值计数并计算概率值（占比）
        if i_p != 0:
            i_logp = np.log2(i_p) # 对数值
            H_X = H_X + (-i_p*i_logp) # 累加
        elif i_p == 0:
            H_X = H_X + 1 # 对于概率值为0的，定义0*log0=1，并累加
    return H_X

（2）经验熵的定义：

实际是对$y$求熵，即$H(Y)$

print('经验熵 =',cal_entropy(y,0))

经验熵 = 0.9709505944546686

（3）**“相对熵”**的定义：

$$H(Y|X)=\sum _{i=1}^{n}H(Y|X=x_i)$$
表示在已知随机变量$X$的条件下随机变量$Y$的不确定性．

def cal_mutualinformation(x,y,i):
    """
    计算第ｉ列的条件熵
        x: 数据
        y: 类别标签
        i: 第ｉ列
    """
    col_i_data = x[:,i]
    data = np.column_stack((col_i_data,y)) # 合并了一个数组，[ｘ_i,y]
    uniquevalue = np.unique(col_i_data) # 查找所有可能的值
    H_YconX = 0 # 统计熵的加和
    H_YconX = 0
    for j in range(len(uniquevalue)):
        D_i = data[col_i_data == uniquevalue[j],:]
        uniqueclass = np.unique(y)
        factor2 = 0
        for k in range(len(uniqueclass)):# H(Di) = sum(|Dik|/Di * log |Dik|/Di)
            D_ik = D_i[D_i[:,1] == uniqueclass[k],:]
            if (D_ik.shape[0] == 0):
                temp2 = 0
            else:
                temp2 = - D_ik.shape[0]/D_i.shape[0] * np.log2(D_ik.shape[0]/D_i.shape[0])
                # print(temp2)
            factor2 = factor2 + temp2
        H_YconX = H_YconX + len(D_i)/len(col_i_data) * factor2
    return H_YconX

5.2.2信息增益

信息增益为

$$g(D,A)=H(D)-H(D|A)$$
表示$A$特征对训练数据$D$的信息增益

for m in range(x.shape[1]):
    print('第',m,'个特征的信息增益值为：',cal_entropy(y,0) - cal_mutualinformation(x,y,m))

第 0 个特征的信息增益值为： 0.08300749985576883
第 1 个特征的信息增益值为： 0.32365019815155627
第 2 个特征的信息增益值为： 0.4199730940219749
第 3 个特征的信息增益值为： 0.36298956253708536

将上面的过程定义成函数

def cal_information_gain(x,y):
    """
    计算每个特征下的信息增益值
    """
    result = []
    for i in range(x.shape[1]):
        value = cal_entropy(y,0) - cal_mutualinformation(x,y,i)
        result.append(value)
    return result
[round(i,3) for i in cal_information_gain(x,y)]

[0.083, 0.324, 0.42, 0.363]

所以上面选择增益最大的(0.42)，即第２个特征（有无房子）
注：

那么，这个特征下，以什么值作为分裂点最合适呢？这就像是我们首先在诸多的特征中决定了使用“有无房子”来作为第一个判断条件，那么这个判断的阈值是什么呢？
是

if('有无房子'>=1):

或是

if('有无房子'>=2):

至此，这里就开始涉及到了决策树的生成过程，注意，从这里开始，就要开始造决策树了！

5.3 ID3生成决策树

ID3算法的核心是在决策树各个节点上应用信息增益准则选择特征，递归构建决策树

input: 训练数据D，特征集A，阈值
output: 决策树
步骤

S1：若$D$中所有实例均属于同一类$C_k$,则$T$为单节点树，并将类$C_k$作为该节点的类别标记，返回$T$；
S2：若$A$为空集，则T为单节点树，将D中实例数最大的类$C_k$作为该节点的类标记，返回$T$；
S3：否则，选取信息增益最大的特征$A_g$；
S4：若信息增益$A_g$小于阈值，则$T$为单节点树（实质是继续分裂下去意义不大了）
S5：否则对$A_g$下的每个可能的值划分为非空子集$D_i$，$D_i$中实例数最大的类作为标记，构建子节点，由节点及其子节点构成$T$，返回$T$
S6：对第$i$个子节点，以$D_i$为训练集，以$A-A_i$为特征集，递归调用S1-S5，得到子树$T_i$，返回$T_i$

• 首先：5.2.2中已经计算得出第一个适合分裂的特征是“有无房子”，这里“有无房子”就是根节点root的第一个判断条件：

注：
这里使用了Graphviz用于显示节点图：关于Graphviz的安装与配置
1.pip install Graphviz
2.官网下载Graphviz的msi安装包，地址：https://graphviz.gitlab.io/_pages/Download/Download_windows.html   
3.配置环境变量 user variable：`C:\Program Files (x86)\Graphviz2.38\bin` ,system variable：`C:\Program Files (x86)\Graphviz2.38\bin\dot.exe`   
4.python代码里加入以下代码：
>>> import os
>>> os.environ["PATH"] += os.pathsep + 'C:\\Program Files (x86)\\Graphviz2.38\\bin'

5.3.1 第1次分裂，构建树的root节点

import os
os.environ["PATH"] += os.pathsep + 'C:\\Program Files (x86)\\Graphviz2.38\\bin'
from graphviz import Digraph
g = Digraph('G',filename='./img/tree.1.gv')
g.edge('F2','?1')
g.edge('F2','?2')
g.format = 'png'
g.view(cleanup=True)

'./img/tree.1.gv.png'

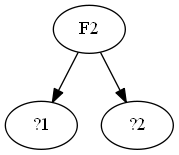
上面的图形，表示首先特征从F2开始分裂，但是F2的分裂条件是什么呢？
根据F2的取值，得到了两类分裂出来的集合：
$D1$和$D2$

D1 = df[df['有自己的房子'] == 1]
D1

	年龄	是否有工作	有自己的房子	信贷情况	类别
3	1	1	1	1	1
7	2	1	1	2	1
8	2	2	1	3	1
9	2	2	1	3	1
10	3	2	1	3	1
11	3	2	1	2	1

D2 = df[df['有自己的房子'] == 2]
D2

	年龄	是否有工作	有自己的房子	信贷情况	类别
0	1	2	2	1	2
1	1	2	2	2	2
2	1	1	2	2	1
4	1	2	2	1	2
5	2	2	2	1	2
6	2	2	2	2	2
12	3	1	2	2	1
13	3	1	2	3	1
14	3	2	2	1	2

读者会发现，D1中的类别标签都是1，所以D1就不用分裂了，因为，仅仅凭借“有自己的房子 == 1”这一个特征，就能决定是属于类别1的
即：
$$(有自己的房子==1)\to (类别==1)$$

g = Digraph('G',filename='./img/tree.2.gv')
g.edge('F2','F2==1')
g.edge('F2','F2==2')
g.edge('F2==1','Label=1,1 step,over')
g.edge('F2==2','?')
g.format = 'png'
g.view(cleanup=True)

'./img/tree.2.gv.png'

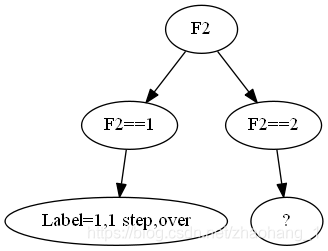
那么剩下的D2怎么办呢？
怎么办？继续分裂呀~

5.3.2 第2次分裂

此时，需要对数据重新计算信息增益值，来确定下次用哪个特征进行分裂！

• 首先，将x剔除“有自己的房子 == 1”这个前提的，生于D2：

index = []
for i in range(len(x)):
    if x[i][2] != 1:
        index.append(i)
# 输出D2的x
D2_x = x[index]
# 输出D2的y
D2_y = y[index]
print('D2_x：\n',D2_x)
print('D2_y：\n',D2_y)

D2_x：
 [[1 2 2 1]
 [1 2 2 2]
 [1 1 2 2]
 [1 2 2 1]
 [2 2 2 1]
 [2 2 2 2]
 [3 1 2 2]
 [3 1 2 3]
 [3 2 2 1]]
D2_y：
 [2 2 1 2 2 2 1 1 2]

• 计算生于特征的信息增益：

[round(i,3) for i in cal_information_gain(D2_x,D2_y)]

[0.252, 0.918, 0.0, 0.474]

此时信息增益最大的特征是F1（有无工作），通过“有无工作”这个特征将数据继续区分为了D3和D4

D3 = D2[D2['是否有工作']==1]
D3

	年龄	是否有工作	有自己的房子	信贷情况	类别
2	1	1	2	2	1
12	3	1	2	2	1
13	3	1	2	3	1

D4 = D2[D2['是否有工作']==2]
D4

	年龄	是否有工作	有自己的房子	信贷情况	类别
0	1	2	2	1	2
1	1	2	2	2	2
4	1	2	2	1	2
5	2	2	2	1	2
6	2	2	2	2	2
14	3	2	2	1	2

此时，发现D3的类别标签都是1，而D4的类别标签都是2，已经完美分开了，所以这次使用这个特征分裂即可！

g = Digraph('G',filename='./img/tree.3.gv')
g.edge('F2','F2==1')
g.edge('F2','F2==2')
g.edge('F2==1','Label=1,1 step,over')
g.edge('F2==2','F1==1')
g.edge('F2==2','F1==2')
g.edge('F1==1','Label=1,2 step,over')
g.edge('F1==2','Label=2,2 step,over')
g.format = 'png'
g.view(cleanup=True)

'./img/tree.3.gv.png'

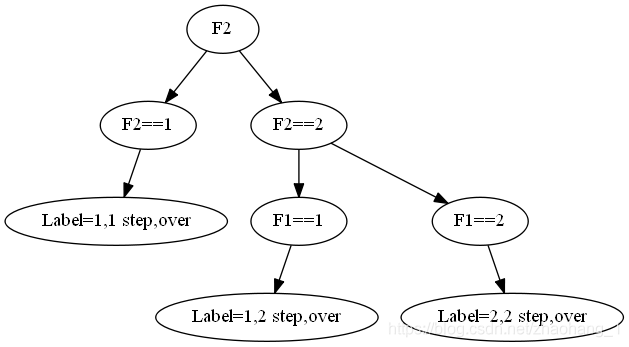
汇总上述的预测过程

label = []
for i in x:
    if i[2]==1:
        label.append(1)
    if i[2]==2:
        if i[1]==1:
            label.append(1)
        if i[1]==2:
            label.append(2)
print('预测类别标签：',np.asarray(label))
print('真实类别标签：',y)
print('准确率：',1.0-sum(np.sign(np.abs(np.asarray(label)-y)))/len(y))

预测类别标签： [2 2 1 1 2 2 2 1 1 1 1 1 1 1 2]
真实类别标签： [2 2 1 1 2 2 2 1 1 1 1 1 1 1 2]
准确率： 1.0

---

5.4 自己写一个决策树函数

暂时使用ID3的策略生成决策树

5.4.1 伪代码

def train(D):
x = D.x
y = D.y

#     S1：如果所有的类别标签都一样为Ck，那么直接返回树
if all y == Ck:
    return T

#     S2：如果子特征集为空，返回T
A = 为已经去掉上一次特征列的新的子特征集
if A == 空:
    return T
else:
    计算A中各特征对D的信息增益，选择Ag（信息增益最大的特征）
    if Ag的信息增益==极小:
        返回Ck
    else:
        对Ag的每个可能值ai，将D分为若干子集Di，Di中实例数最大的类别作为标记

5.4.2 按照书上的详细输出每个步骤产生的输出

# 算法的输入数据初始化D、A、epsilon
#################################################################################################
# 准备数据
import numpy as np
x = np.asarray([[1,2,2,1],[1,2,2,2],[1,1,2,2],[1,1,1,1],[1,2,2,1],
               [2,2,2,1],[2,2,2,2],[2,1,1,2],[2,2,1,3],[2,2,1,3],
               [3,2,1,3],[3,2,1,2],[3,1,2,2],[3,1,2,3],[3,2,2,1]])
y = np.asarray([2,2,1,1,2,2,2,1,1,1,1,1,1,1,2])
#################################################################################################
level = 0
D = []
D.append(x)
D.append(y)
A = set(range(4))
epsilon = 0.01
def f(D,A):
    print('------------------------------------------------------------------------------------')
    x = D[0]
    y = D[1]
    print('\n'+'**'*15,'-输入-','**'*15)
    print('训练数据集\n\tD =：',D)
    print('特征集    \n\tA =：',A)
    print('阈值    \n\tepsilon =：',epsilon)
    #############################################################################################
    print('\n'+'**'*15,'-S1-','**'*15)
    if len(np.unique(y))==1:
        print('【模型参数】所有实例都为同一个类别标签',np.unique(y),'，在此终止，将会返回树T.')
    else:
        print('D中所有实例隶属于不同的类别标签→S2')

        #############################################################################################
        print('\n'+'**'*15,'-S2-','**'*15)
        if len(A)==0:
            print('A已经没有特征需要分析了，在此终止，将会返回树T.')
        elif len(A)>0:
            print('A不为空，将继续执行→S3')

            #############################################################################################
            print('\n'+'**'*15,'-S3-','**'*15)
            max_gain_col = np.argmax(cal_information_gain(x,y))
            print('信息增益最大的列：为第',max_gain_col,'列，即Ag =',max_gain_col,'，其中信息增益值 =',cal_information_gain(x,y)[max_gain_col],'，将继续执行→S4')
            print('【模型参数】：分裂特征Index =',max_gain_col)

            #############################################################################################
            print('\n'+'**'*15,'-S4-','**'*15)
            if cal_information_gain(x,y)[max_gain_col] < epsilon:
                print('特征产生的信息增益过小，在此终止，将会返回树T.')
            else:
                print('信息增益值大于epsilon(',str(epsilon),')，将继续执行，将继续执行→S5')

                #############################################################################################    
                print('\n'+'**'*15,'-S5-','**'*15)
                print('该特征所有可以分裂的节点包含了：',np.unique(x[:,max_gain_col]))
                Di_x = []
                Di_y = []
                for i in np.unique(x[:,max_gain_col]):
                    Di_x.append(x[x[:,max_gain_col] == i])
                    Di_y.append(y[x[:,max_gain_col] == i])
                for i in range(len(np.unique(x[:,max_gain_col]))):
                    print('当第',str(max_gain_col),'列属性的值等于',np.unique(x[:,max_gain_col])[i],'时','D(',str(i),')=',Di_x[i],Di_y[i])
                for i in Di_y:
                    max_count = -1
                    max_count_class = -1
                    for j in np.unique(i):
                        count = list(i).count(j)
                        if max_count<count:
                            max_count = count
                            max_count_class = j
                    print('实例数最大的类是：',max_count_class,'，包含的样本数是：',max_count)
                    print('【模型参数】：类别标签是',max_count_class)
                #############################################################################################
                print('\n'+'**'*15,'-S6-','**'*15)
                A.remove(max_gain_col)
                print('【模型参数】：目前的A =',A)
                for i in range(len(Di_x)):
                    Di = [Di_x[i],Di_y[i]]
                    f(Di,A)
        
f(D,A)

------------------------------------------------------------------------------------

****************************** -输入- ******************************
训练数据集
	D =： [array([[1, 2, 2, 1],
       [1, 2, 2, 2],
       [1, 1, 2, 2],
       [1, 1, 1, 1],
       [1, 2, 2, 1],
       [2, 2, 2, 1],
       [2, 2, 2, 2],
       [2, 1, 1, 2],
       [2, 2, 1, 3],
       [2, 2, 1, 3],
       [3, 2, 1, 3],
       [3, 2, 1, 2],
       [3, 1, 2, 2],
       [3, 1, 2, 3],
       [3, 2, 2, 1]]), array([2, 2, 1, 1, 2, 2, 2, 1, 1, 1, 1, 1, 1, 1, 2])]
特征集    
	A =： {0, 1, 2, 3}
阈值    
	epsilon =： 0.01

****************************** -S1- ******************************
D中所有实例隶属于不同的类别标签→S2

****************************** -S2- ******************************
A不为空，将继续执行→S3

****************************** -S3- ******************************
信息增益最大的列：为第 2 列，即Ag = 2 ，其中信息增益值 = 0.4199730940219749 ，将继续执行→S4
【模型参数】：分裂特征Index = 2

****************************** -S4- ******************************
信息增益值大于epsilon( 0.01 )，将继续执行，将继续执行→S5

****************************** -S5- ******************************
该特征所有可以分裂的节点包含了： [1 2]
当第 2 列属性的值等于 1 时 D( 0 )= [[1 1 1 1]
 [2 1 1 2]
 [2 2 1 3]
 [2 2 1 3]
 [3 2 1 3]
 [3 2 1 2]] [1 1 1 1 1 1]
当第 2 列属性的值等于 2 时 D( 1 )= [[1 2 2 1]
 [1 2 2 2]
 [1 1 2 2]
 [1 2 2 1]
 [2 2 2 1]
 [2 2 2 2]
 [3 1 2 2]
 [3 1 2 3]
 [3 2 2 1]] [2 2 1 2 2 2 1 1 2]
实例数最大的类是： 1 ，包含的样本数是： 6
【模型参数】：类别标签是 1
实例数最大的类是： 2 ，包含的样本数是： 6
【模型参数】：类别标签是 2

****************************** -S6- ******************************
【模型参数】：目前的A = {0, 1, 3}
------------------------------------------------------------------------------------

****************************** -输入- ******************************
训练数据集
	D =： [array([[1, 1, 1, 1],
       [2, 1, 1, 2],
       [2, 2, 1, 3],
       [2, 2, 1, 3],
       [3, 2, 1, 3],
       [3, 2, 1, 2]]), array([1, 1, 1, 1, 1, 1])]
特征集    
	A =： {0, 1, 3}
阈值    
	epsilon =： 0.01

****************************** -S1- ******************************
【模型参数】所有实例都为同一个类别标签 [1] ，在此终止，将会返回树T.
------------------------------------------------------------------------------------

****************************** -输入- ******************************
训练数据集
	D =： [array([[1, 2, 2, 1],
       [1, 2, 2, 2],
       [1, 1, 2, 2],
       [1, 2, 2, 1],
       [2, 2, 2, 1],
       [2, 2, 2, 2],
       [3, 1, 2, 2],
       [3, 1, 2, 3],
       [3, 2, 2, 1]]), array([2, 2, 1, 2, 2, 2, 1, 1, 2])]
特征集    
	A =： {0, 1, 3}
阈值    
	epsilon =： 0.01

****************************** -S1- ******************************
D中所有实例隶属于不同的类别标签→S2

****************************** -S2- ******************************
A不为空，将继续执行→S3

****************************** -S3- ******************************
信息增益最大的列：为第 1 列，即Ag = 1 ，其中信息增益值 = 0.9182958340544896 ，将继续执行→S4
【模型参数】：分裂特征Index = 1

****************************** -S4- ******************************
信息增益值大于epsilon( 0.01 )，将继续执行，将继续执行→S5

****************************** -S5- ******************************
该特征所有可以分裂的节点包含了： [1 2]
当第 1 列属性的值等于 1 时 D( 0 )= [[1 1 2 2]
 [3 1 2 2]
 [3 1 2 3]] [1 1 1]
当第 1 列属性的值等于 2 时 D( 1 )= [[1 2 2 1]
 [1 2 2 2]
 [1 2 2 1]
 [2 2 2 1]
 [2 2 2 2]
 [3 2 2 1]] [2 2 2 2 2 2]
实例数最大的类是： 1 ，包含的样本数是： 3
【模型参数】：类别标签是 1
实例数最大的类是： 2 ，包含的样本数是： 6
【模型参数】：类别标签是 2

****************************** -S6- ******************************
【模型参数】：目前的A = {0, 3}
------------------------------------------------------------------------------------

****************************** -输入- ******************************
训练数据集
	D =： [array([[1, 1, 2, 2],
       [3, 1, 2, 2],
       [3, 1, 2, 3]]), array([1, 1, 1])]
特征集    
	A =： {0, 3}
阈值    
	epsilon =： 0.01

****************************** -S1- ******************************
【模型参数】所有实例都为同一个类别标签 [1] ，在此终止，将会返回树T.
------------------------------------------------------------------------------------

****************************** -输入- ******************************
训练数据集
	D =： [array([[1, 2, 2, 1],
       [1, 2, 2, 2],
       [1, 2, 2, 1],
       [2, 2, 2, 1],
       [2, 2, 2, 2],
       [3, 2, 2, 1]]), array([2, 2, 2, 2, 2, 2])]
特征集    
	A =： {0, 3}
阈值    
	epsilon =： 0.01

****************************** -S1- ******************************
【模型参数】所有实例都为同一个类别标签 [2] ，在此终止，将会返回树T.

5.4.3 以下化简了输出，以方便查看决策树的决策流程

# 算法的输入数据初始化D、A、epsilon
#################################################################################################
# 准备数据
import numpy as np
x = np.asarray([[1,2,2,1],[1,2,2,2],[1,1,2,2],[1,1,1,1],[1,2,2,1],
               [2,2,2,1],[2,2,2,2],[2,1,1,2],[2,2,1,3],[2,2,1,3],
               [3,2,1,3],[3,2,1,2],[3,1,2,2],[3,1,2,3],[3,2,2,1]])
y = np.asarray([2,2,1,1,2,2,2,1,1,1,1,1,1,1,2])
#################################################################################################
level = 0
D = []
D.append(x)
D.append(y)
A = set(range(4))
epsilon = 0.01
def f(D,A,level = 0):
    if level==0:
        print('--------------------------------------level = ',str(0),'--------------------------------------------')
    level = level + 1 
    x = D[0]
    y = D[1]
    if len(np.unique(y))==1:
        print('  '*level,'【      模型参数】在本Di分支中所有实例的标签一样，Label =',np.unique(y),'，在此终止，将会返回树T.')
    else:
        if len(A)==0:
            print('A已经没有特征需要分析了，在此终止，将会返回树T.')
        elif len(A)>0:
            max_gain_col = np.argmax(cal_information_gain(x,y))
            print('  '*level,'【      模型参数】：分裂第i =',max_gain_col,'个特征（i 属于 ',set(range(x.shape[1])),',可以产生的信息增益为',round(cal_information_gain(x,y)[max_gain_col],3))
            if cal_information_gain(x,y)[max_gain_col] < epsilon:
                print('  '*level,'特征产生的信息增益过小，在此终止，将会返回树T.')
            else:
                Di_x = []
                Di_y = []
                for i in np.unique(x[:,max_gain_col]):
                    Di_x.append(x[x[:,max_gain_col] == i])
                    Di_y.append(y[x[:,max_gain_col] == i])
                for i in Di_y:
                    max_count = -1
                    max_count_class = -1
                    for j in np.unique(i):
                        count = list(i).count(j)
                        if max_count<count:
                            max_count = count
                            max_count_class = j
                    print('  '*level,'【子节点模型参数】：可以分裂出类别标签',max_count_class)
                A.remove(max_gain_col)
                for i in range(len(Di_x)):
                    Di = [Di_x[i],Di_y[i]]
                    print('>>'*level,'--------------------------------------level = ',str(level),'--------------------------------------------')
                    print('  '*level,'【条件参数】：if x[ i,',max_gain_col,'] =',str(Di[0][0,max_gain_col]),':')
                    print('  '*level,Di)
                    f(Di,A,level)

f(D,A)

--------------------------------------level =  0 --------------------------------------------
   【      模型参数】：分裂第i = 2 个特征（i 属于  {0, 1, 2, 3} ,可以产生的信息增益为 0.42
   【子节点模型参数】：可以分裂出类别标签 1
   【子节点模型参数】：可以分裂出类别标签 2
>> --------------------------------------level =  1 --------------------------------------------
   【条件参数】：if x[ i, 2 ] = 1 :
   [array([[1, 1, 1, 1],
       [2, 1, 1, 2],
       [2, 2, 1, 3],
       [2, 2, 1, 3],
       [3, 2, 1, 3],
       [3, 2, 1, 2]]), array([1, 1, 1, 1, 1, 1])]
     【      模型参数】在本Di分支中所有实例的标签一样，Label = [1] ，在此终止，将会返回树T.
>> --------------------------------------level =  1 --------------------------------------------
   【条件参数】：if x[ i, 2 ] = 2 :
   [array([[1, 2, 2, 1],
       [1, 2, 2, 2],
       [1, 1, 2, 2],
       [1, 2, 2, 1],
       [2, 2, 2, 1],
       [2, 2, 2, 2],
       [3, 1, 2, 2],
       [3, 1, 2, 3],
       [3, 2, 2, 1]]), array([2, 2, 1, 2, 2, 2, 1, 1, 2])]
     【      模型参数】：分裂第i = 1 个特征（i 属于  {0, 1, 2, 3} ,可以产生的信息增益为 0.918
     【子节点模型参数】：可以分裂出类别标签 1
     【子节点模型参数】：可以分裂出类别标签 2
>>>> --------------------------------------level =  2 --------------------------------------------
     【条件参数】：if x[ i, 1 ] = 1 :
     [array([[1, 1, 2, 2],
       [3, 1, 2, 2],
       [3, 1, 2, 3]]), array([1, 1, 1])]
       【      模型参数】在本Di分支中所有实例的标签一样，Label = [1] ，在此终止，将会返回树T.
>>>> --------------------------------------level =  2 --------------------------------------------
     【条件参数】：if x[ i, 1 ] = 2 :
     [array([[1, 2, 2, 1],
       [1, 2, 2, 2],
       [1, 2, 2, 1],
       [2, 2, 2, 1],
       [2, 2, 2, 2],
       [3, 2, 2, 1]]), array([2, 2, 2, 2, 2, 2])]
       【      模型参数】在本Di分支中所有实例的标签一样，Label = [2] ，在此终止，将会返回树T.

上面的“条件参数”顺序是这样的：

if x[ i, 2 ] = 1 :
    Label = 1
if x[ i, 2 ] = 2 :
    if x[ i, 1 ] = 1 :
        Label = 1
    if x[ i, 1 ] = 1 :
        Label = 2

至此，决策树就生成了！