题目:
一个数组实现两个栈。
方法1:
下标为0的位置为栈1的栈底,下标为1的位置为栈2的栈底,栈1的元素存放在下标为偶数的位置上,栈2的元素放在下标为奇数的位置上。
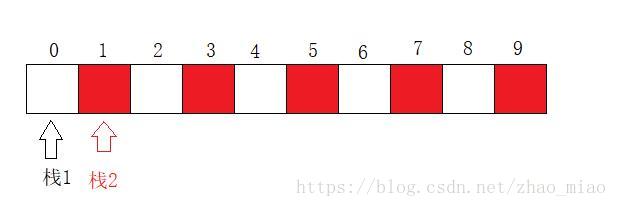
| 如上图所示的数组:若栈1有一个元素 2,栈2有6个元素 1,2,3,4,5,6,下标为0的位置为 2,下标为1,3,5,7,9的位置分别为1,2,3,4,5。6无法插入但数组中还有很多剩余的空间。。可见该方法会浪费大量的空间。 |
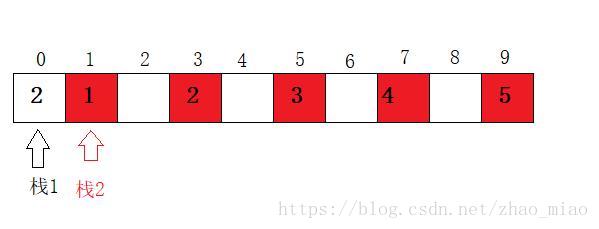
方法2:
中间的两个下标分别作为栈1和栈2的栈底,栈1和栈2分别向左右扩展。
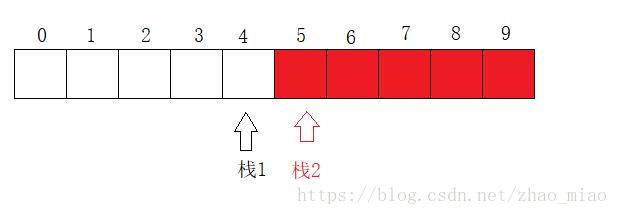
如方法1所示,方法2与方法1相似也会浪费大量的空间。
方法3:
下标为0的位置为栈1的栈底,栈2的栈底在下标最大的位置上。栈1向左扩展,栈2向后扩展。这种方法不会出现浪费内存的情况。
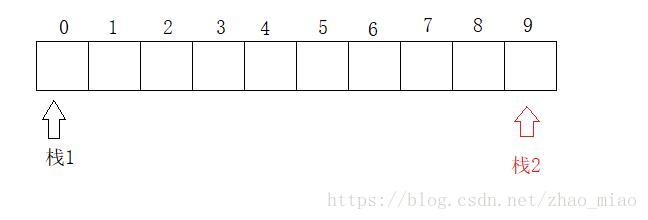
方法3的代码实现:
首先应该定义一个共享栈:
#define Max 10
#define DataType int
typedef struct SharedStack
{
DataType data[Max];
int top1;
int top2;
}sharedstack;共享栈初始化:
//共享栈初始化
void InitShared(sharedstack *s)
{
assert(s);
s->top1 = 0;
s->top2 = Max - 1;
memset(s->data, 0, Max*sizeof(DataType));
}入栈:
//入栈
void PushSharedStack(sharedstack *s, DataType d, int which)
{
assert(s);
if (which == 1)
{
if (s->top1 <= s->top2)
{
s->data[s->top1++] = d;
}
else
{
printf("栈已满!\n");
return;
}
}
else
{
if (s->top1 <= s->top2)
{
s->data[s->top2--] = d;
}
else
{
printf("栈已满!\n");
return;
}
}
}| which == 1 表示栈1,d表示要入栈的数据。 |
出栈:
//出栈
void PopSharedStack(sharedstack *s, int which)
{
assert(s);
if (which == 1)
{
if (s->top1 == 0)
{
printf("栈空!\n");
return;
}
else
{
s->top1--;
}
}
else
{
if (s->top2 == Max-1)
{
printf("栈空!\n");
return;
}
else
{
s->top2++;
}
}
}栈顶元素:
//栈顶
DataType SharedStackTop(sharedstack *s, int which)
{
assert(s);
if (which == 1)
{
if (s->top1 == 0)
{
printf("栈空!\n");
return -1;
}
else
return s->data[s->top1 - 1];
}
else
{
if (s->top2 == Max-1)
{
printf("栈空!\n");
return -1;
}
else
return s->data[s->top2 + 1];
}
}栈长短:
//栈长短
DataType SharedStackSize(sharedstack *s, int which)
{
assert(s);
if (which == 1)
{
return s->top1;
}
else
return Max - s->top2 - 1;
}







 本文探讨了一种在单一数组中实现两个独立栈的有效方法。通过对比三种不同的实现方案,详细阐述了方法3的优势,即避免了空间浪费,实现了栈1和栈2的高效存储与操作。文章提供了具体的代码实现,包括栈的初始化、入栈、出栈和获取栈顶元素等功能。
本文探讨了一种在单一数组中实现两个独立栈的有效方法。通过对比三种不同的实现方案,详细阐述了方法3的优势,即避免了空间浪费,实现了栈1和栈2的高效存储与操作。文章提供了具体的代码实现,包括栈的初始化、入栈、出栈和获取栈顶元素等功能。
















 2162
2162

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








