秋招END

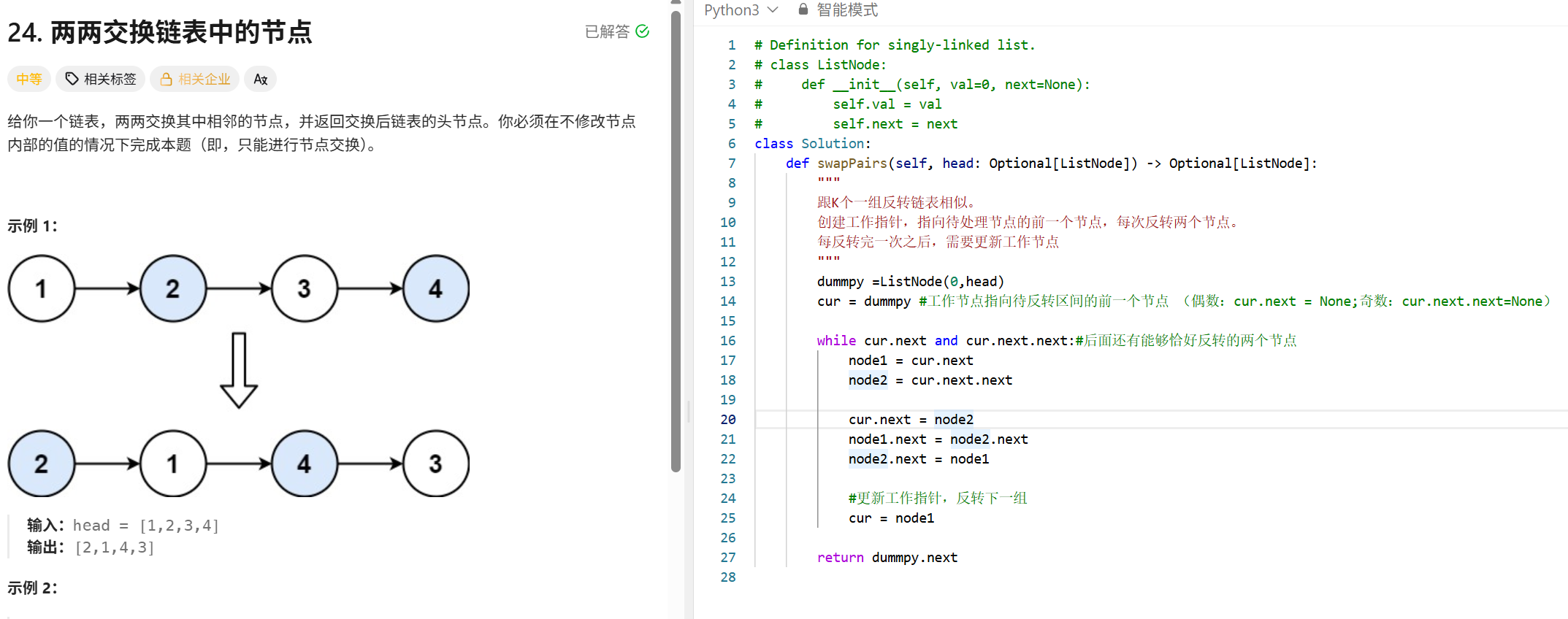
主管面+hr

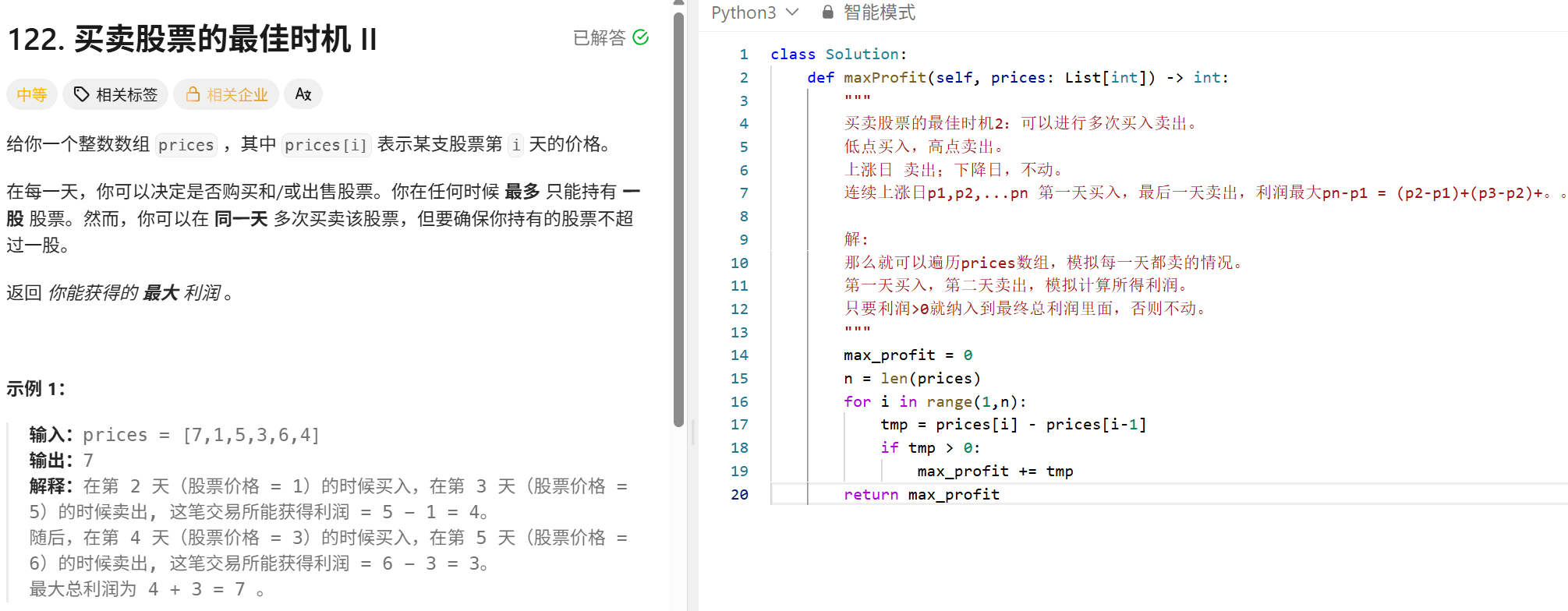
当面对压力的时候，应该怎么做？

面对压力首先一定…

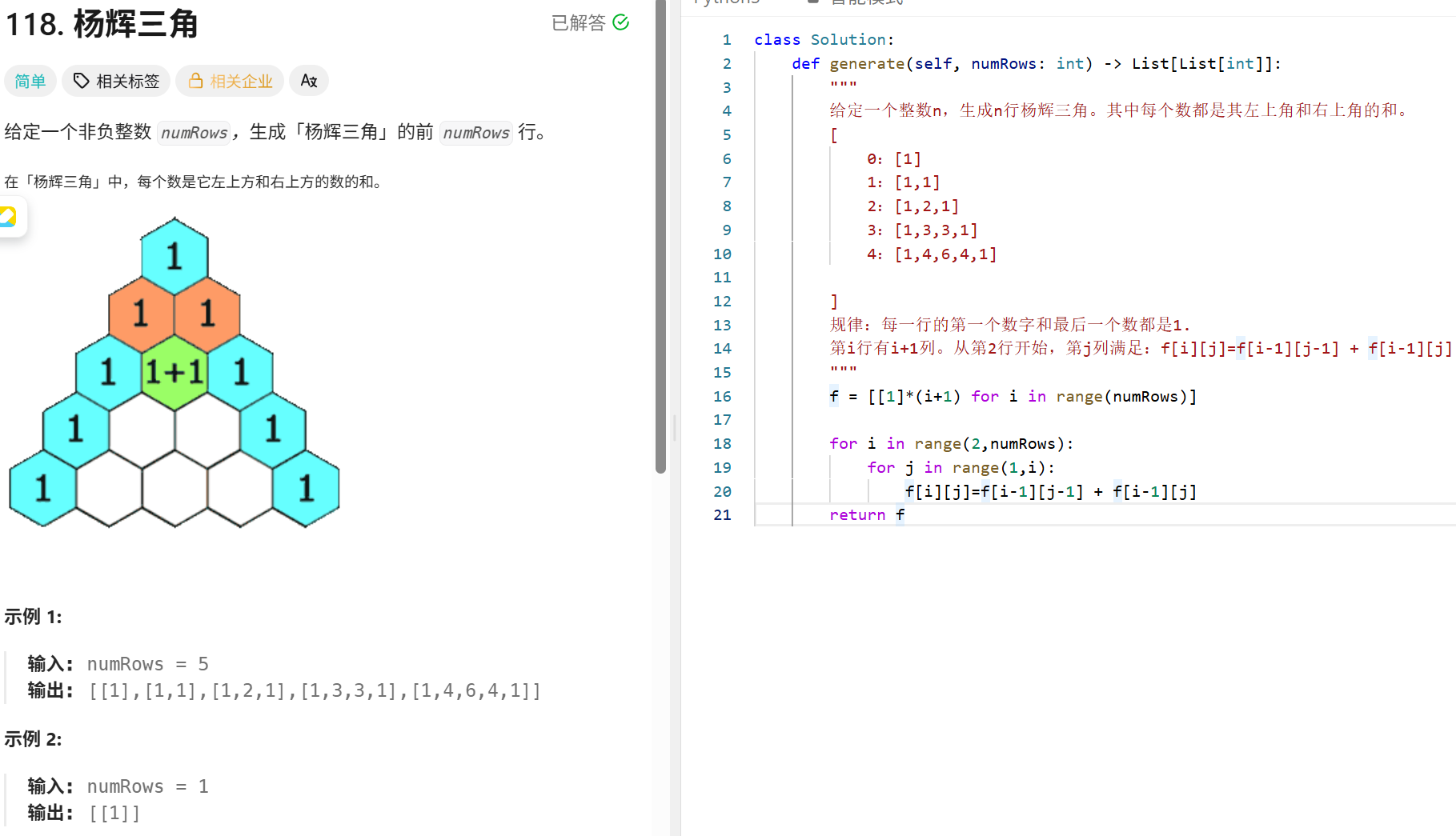
实习收获：

在实习期间，我最大的收获是…

我的优缺点？

优点：

我做事比较…

缺点：

我可能有时候比较…

相较于其他同学你个人的优势？

我觉得我…

你能给团队带来什么？

• 我觉得能带来一些…

对加班的看法？

• 我对加班倒是没什么排斥的…

为什么来XX？

…

未来职业规划？

1. 我未来就打算一直做…

想做哪些方向？

我比较想做…

过去的学习当中遇到过哪些很大的挫折，怎么解决的？

在学习过程中我遇到过…

遇到和同事分歧的时候

首先先分析下原因,…

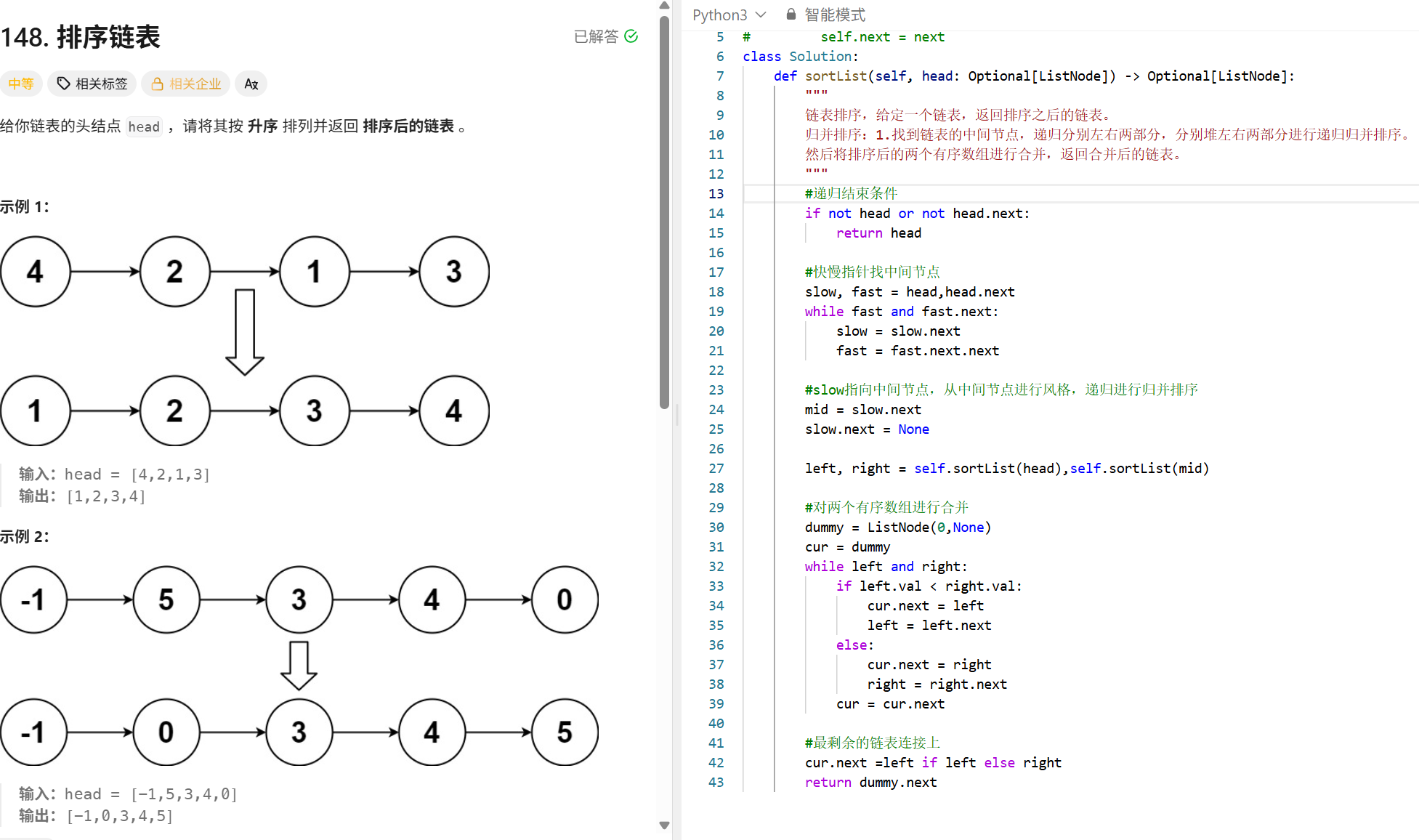
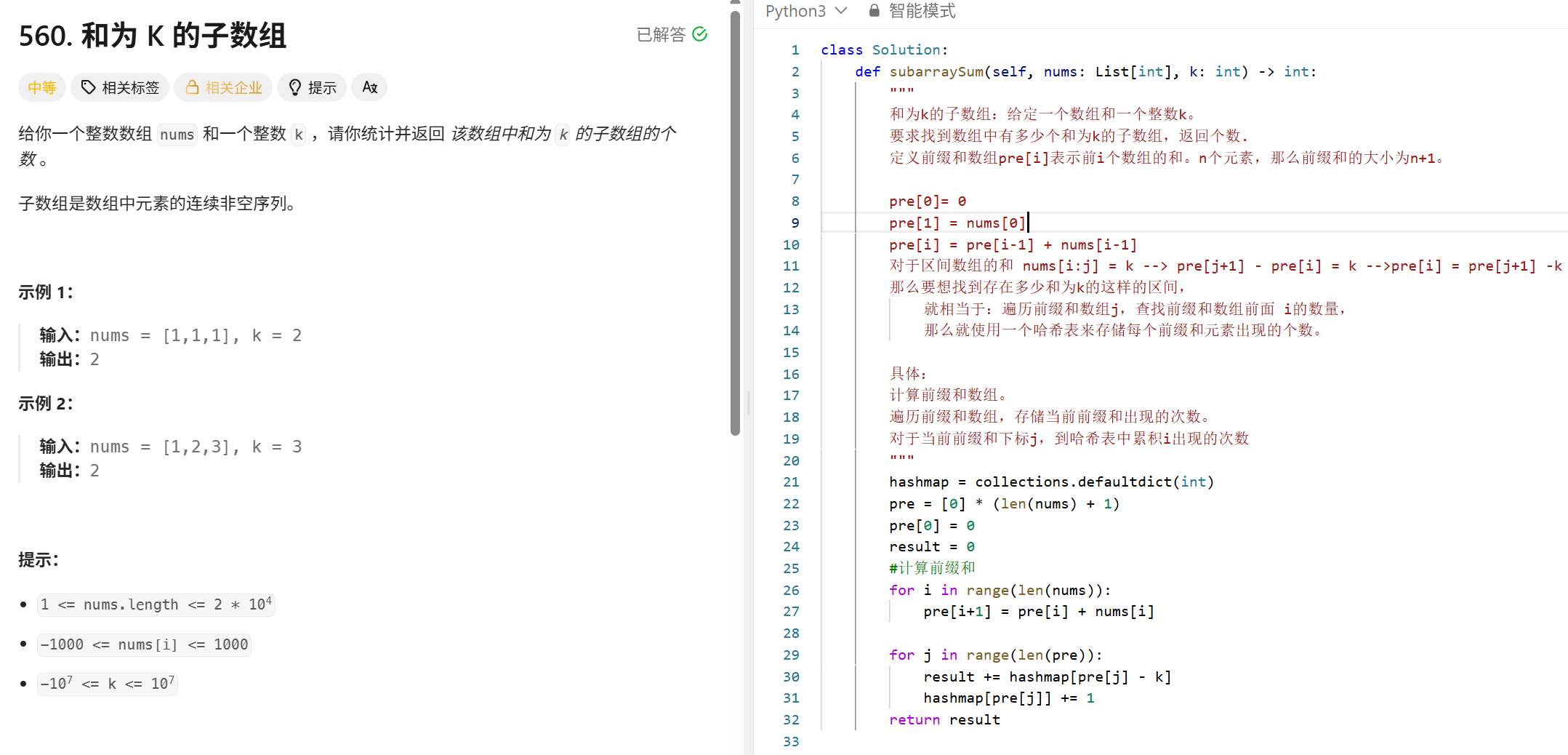
机器学习

KMeans

import numpy as np

class KMeans:
    def __init__(self,k=3,max_iters=100,epsilon=1e-4):
        self.k = k
        self.max_iters=max_iters
        self.epsilon=epsilon

    def fit(self,X):
        #随机选取K个初始簇中心
        n_samples,n_features = X.shape
        random_idx = np.random.choice(n_samples,self.k,replace=True)
        self.centroids = X[random_idx]

        #进行循环
        for _ in range(self.max_iters):
            #分配每个样本到最近的簇中心
            labels = self._assign_clusters(X)

            #重新计算簇中心  找出第i个簇的所有样本进行特征均值计算
            new_centroids = np.array([
                X[labels ==i].mean(axis=0) if np.any(labels == i) else self.centroids[i] for i in range(self.k)
            ])
            #判断是否已经收敛
            if np.linalg.norm(new_centroids - self.centroids) < self.epsilon:
                break
            self.centroids = new_centroids
        #在训练后保存每个样本所属的标签
        self.labels_ = self._assign_clusters(X)

    def _assign_clusters(self,X):
        distances = np.linalg.norm(X[:,np.newaxis] - self.centroids,axis=2)
        return np.argmin(distances,axis=1)

    def predict(self,X):
        return self._assign_clusters(X)
    

KNN：

import numpy as np
from collections import Counter

class KNN:
    def __init__(self, k=3):
        self.k = k

    def fit(self, X_train, y_train):
        self.X_train = np.array(X_train)
        self.y_train = np.array(y_train)

    def predict(self, X_test):
        preds = []
        for x in X_test:
            # 1. 计算距离
            distances = np.sqrt(np.sum((self.X_train - x) ** 2, axis=1))
            # 2. 取最近的 k 个邻居
            k_idx = np.argsort(distances)[:self.k]
            k_labels = self.y_train[k_idx]
            # 3. 投票
            pred = Counter(k_labels).most_common(1)[0][0]
            preds.append(pred)
        return np.array(preds)

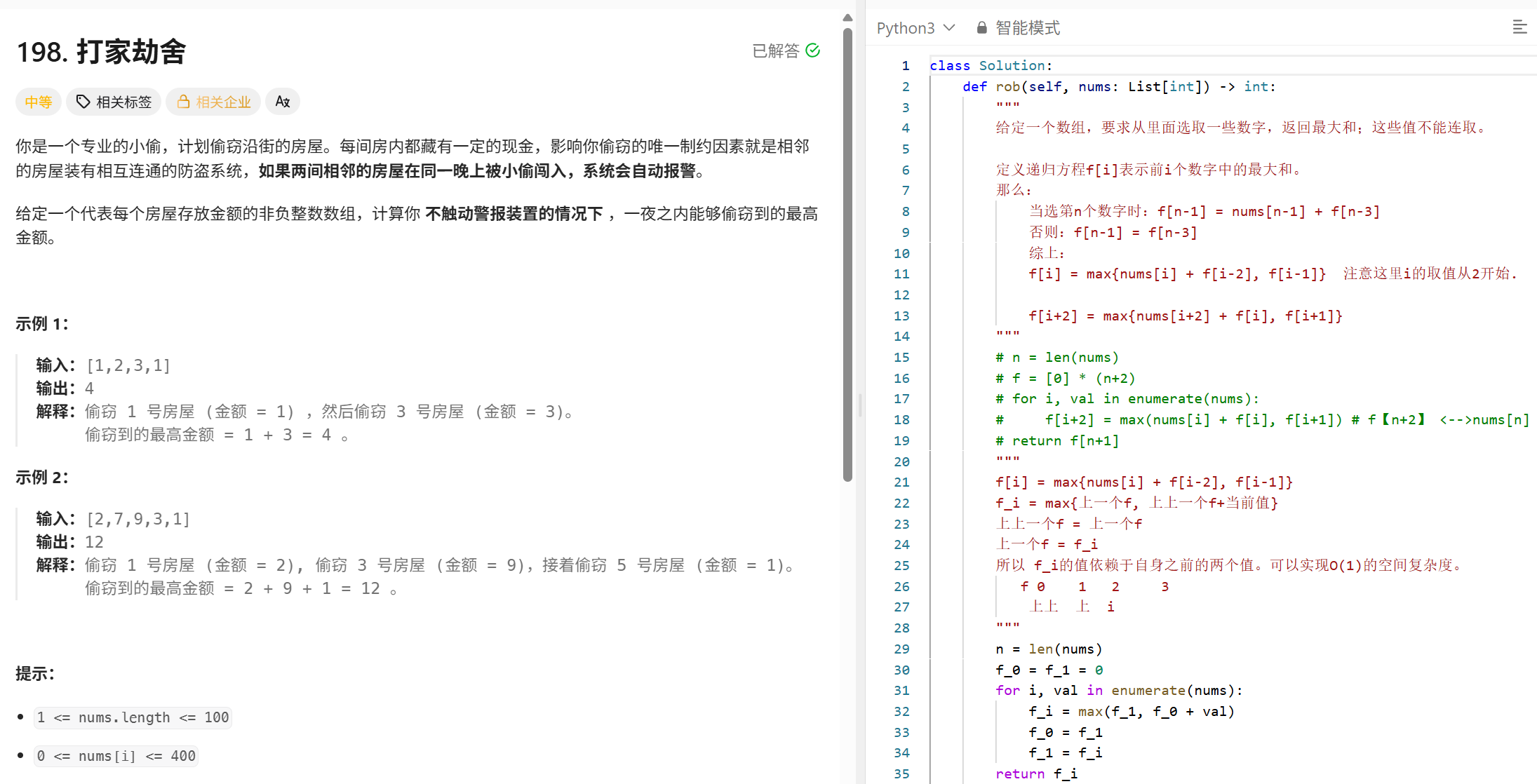
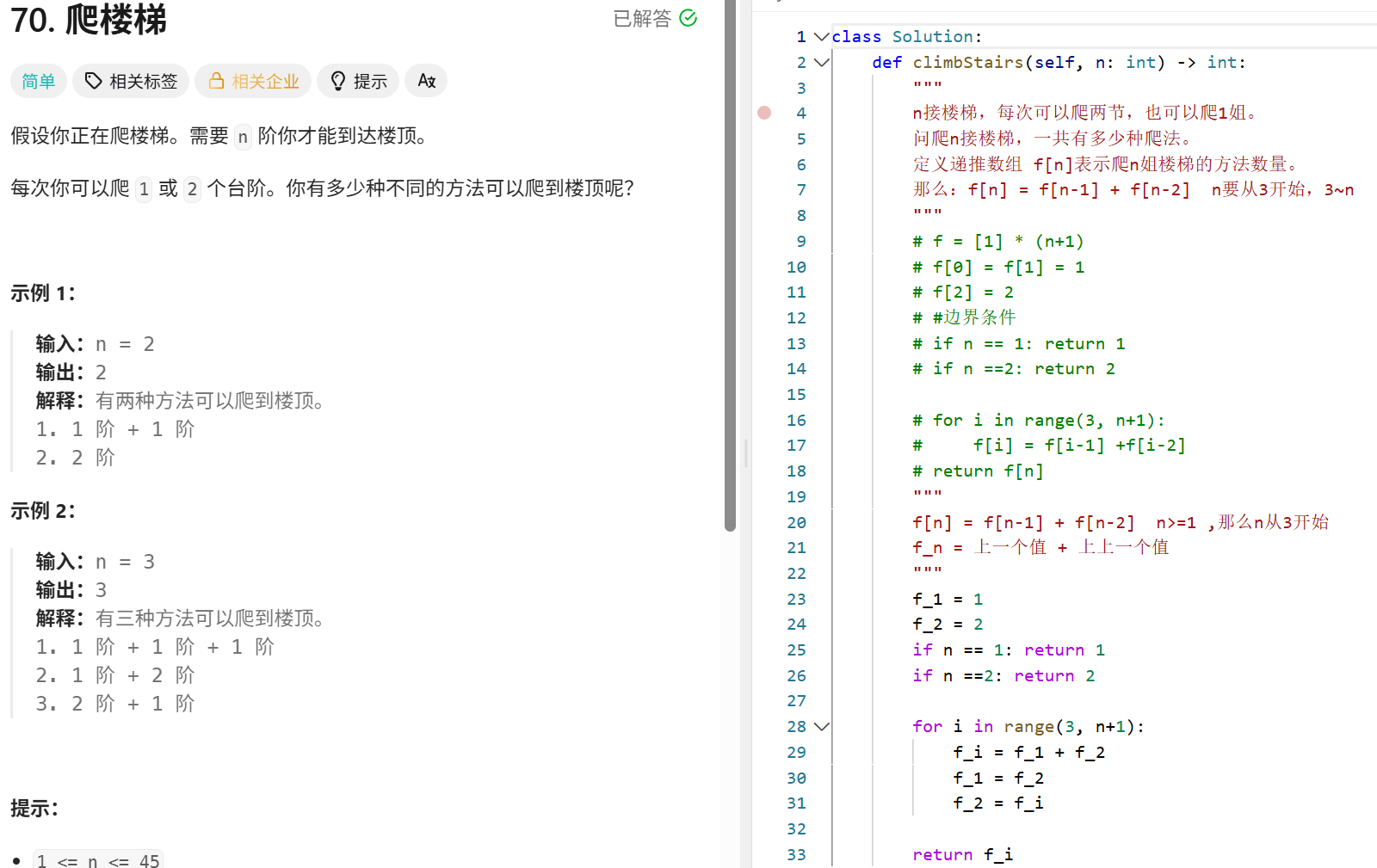
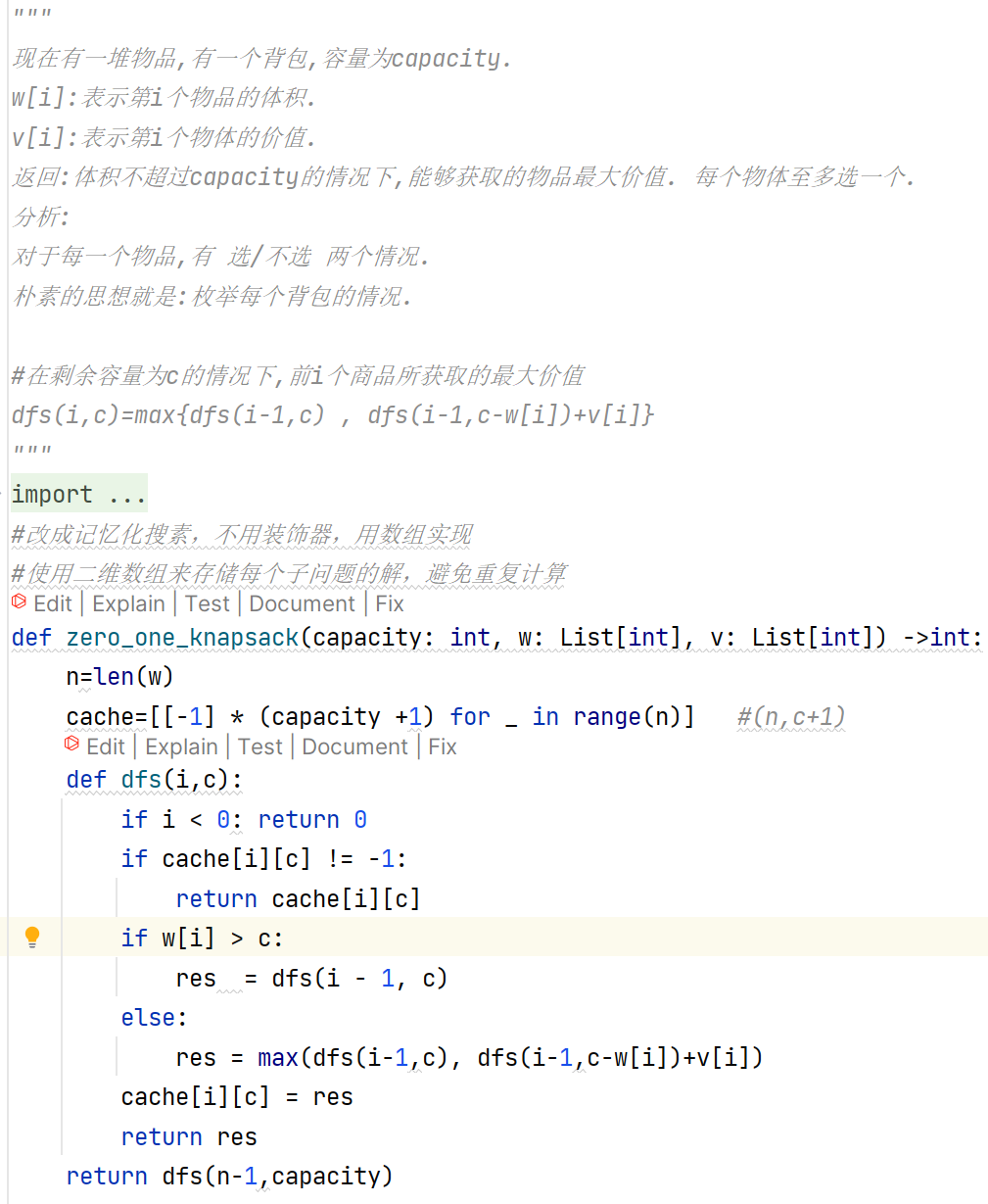
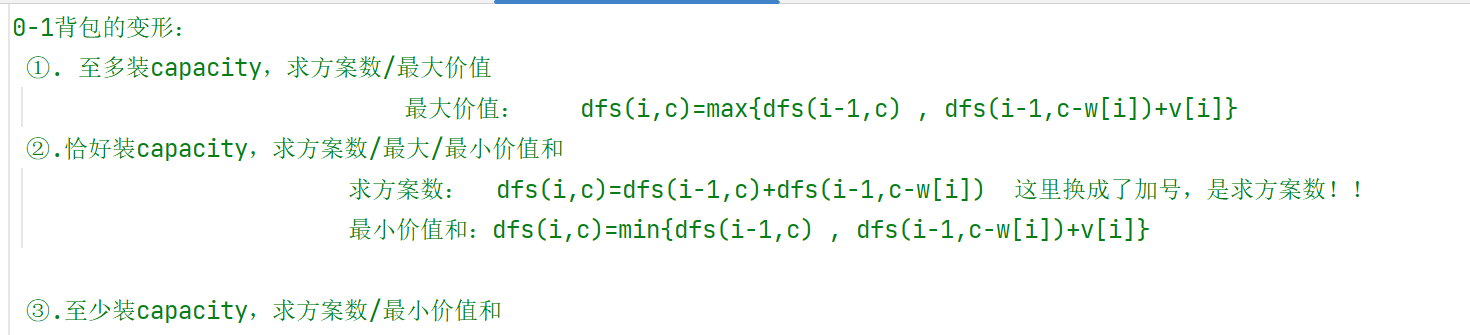
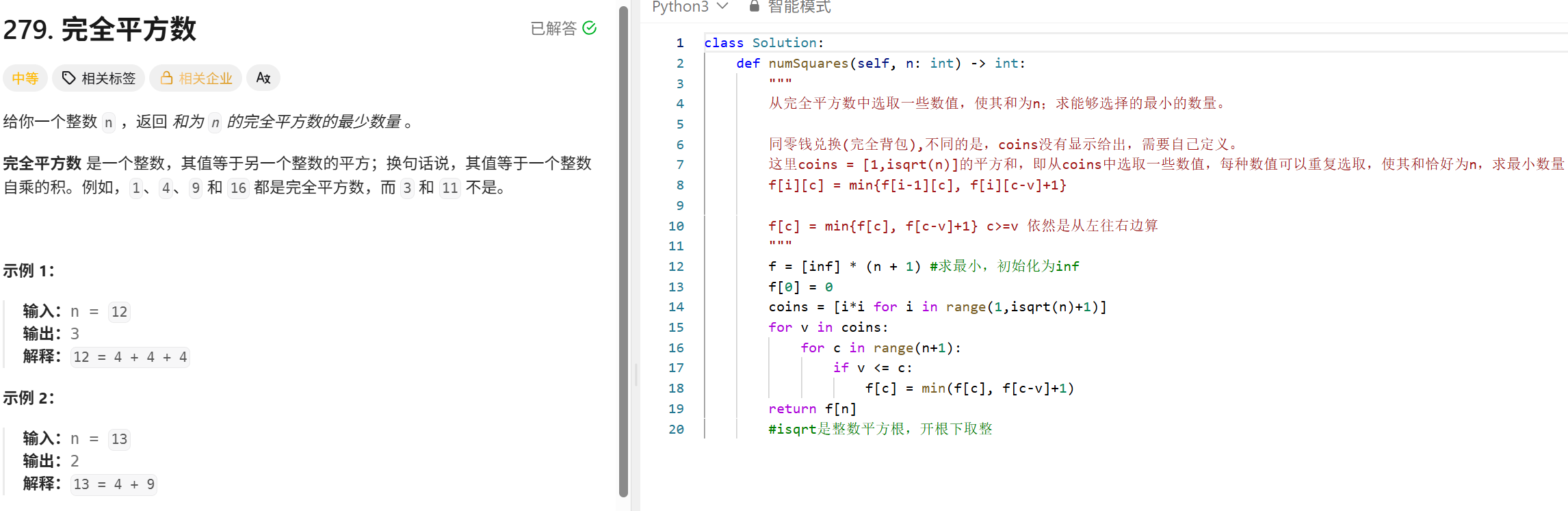
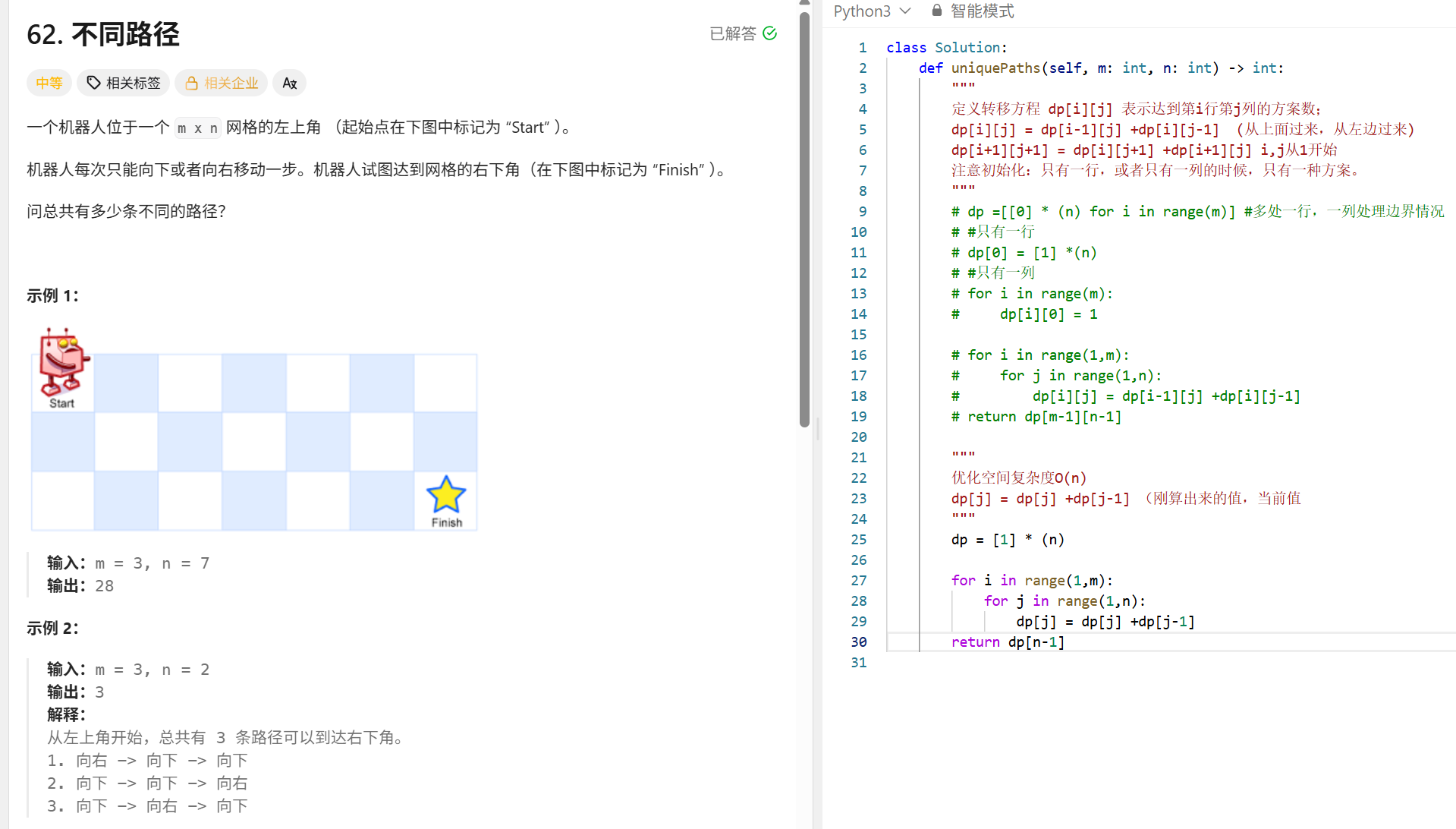
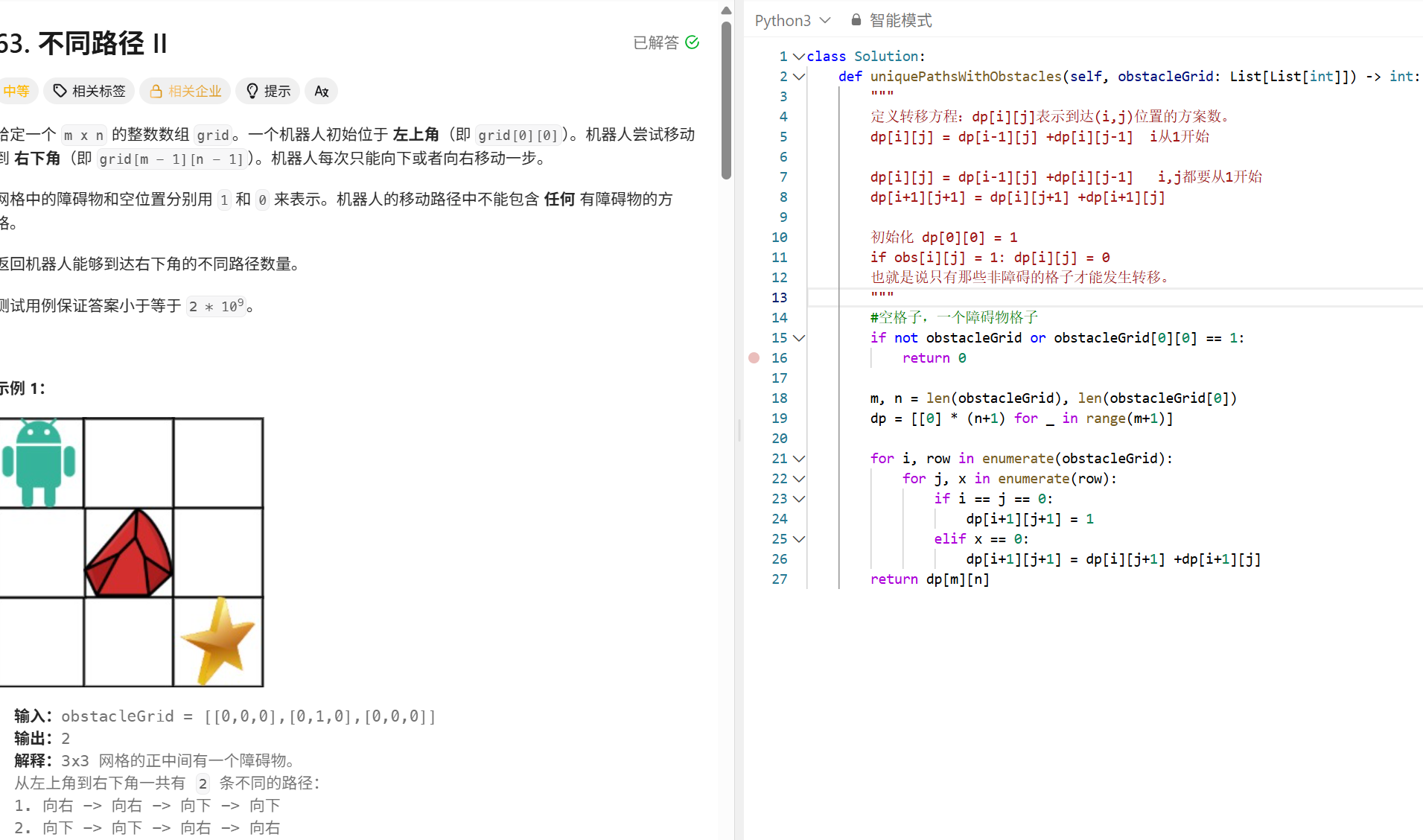
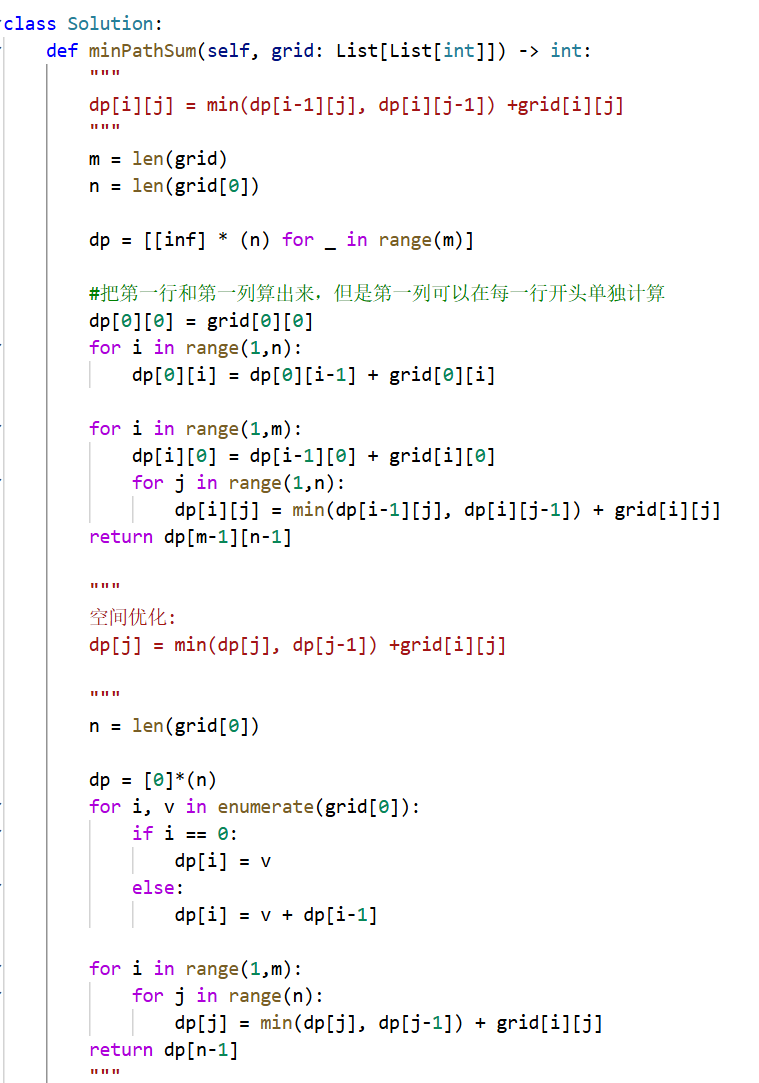
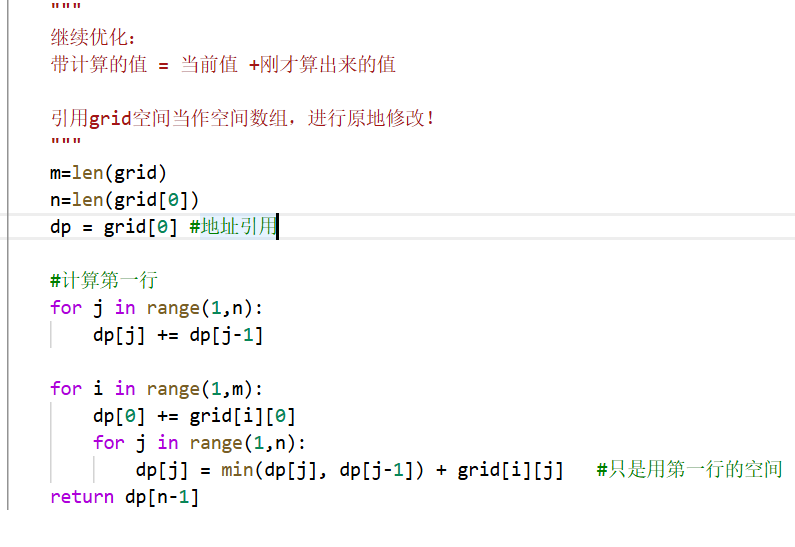
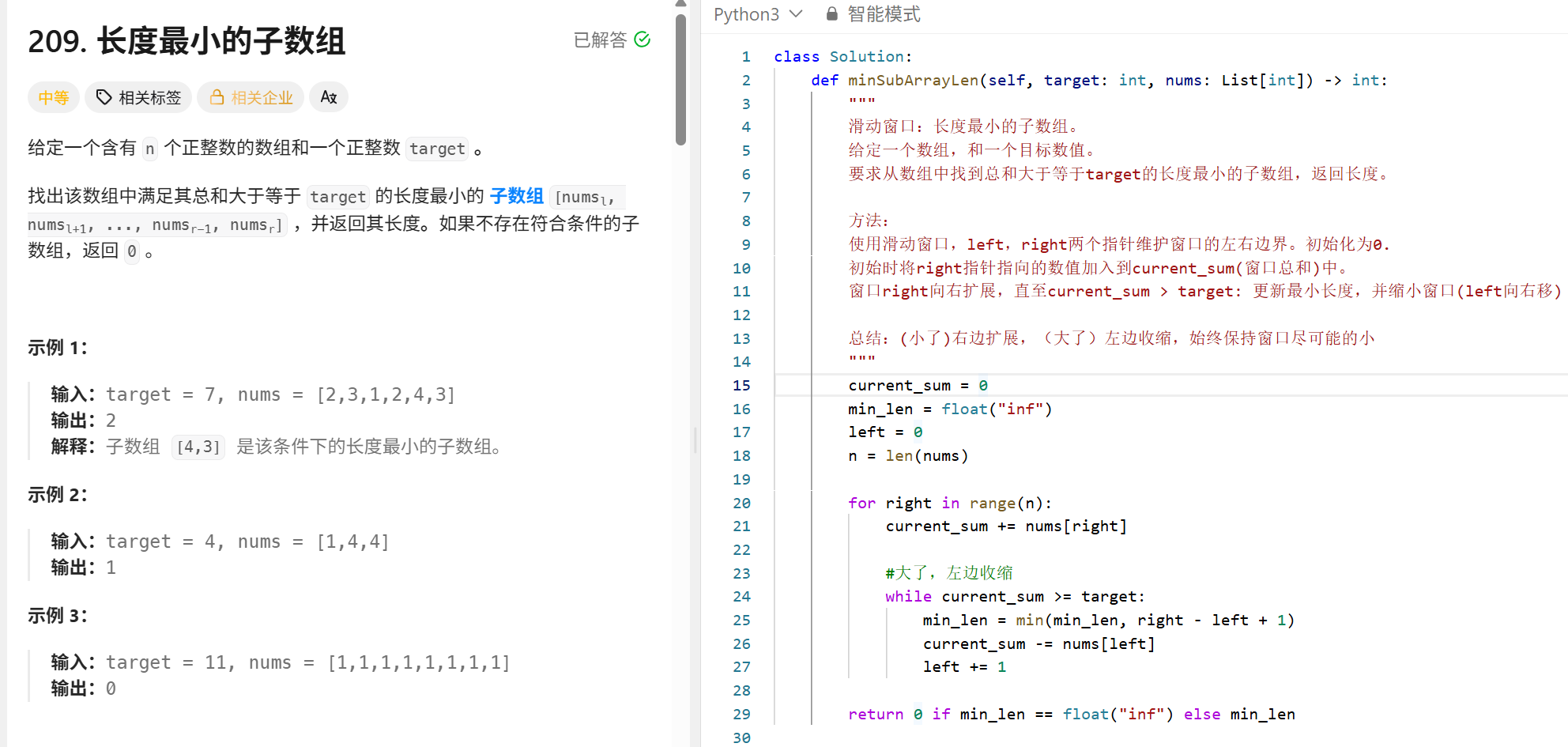
动态规划

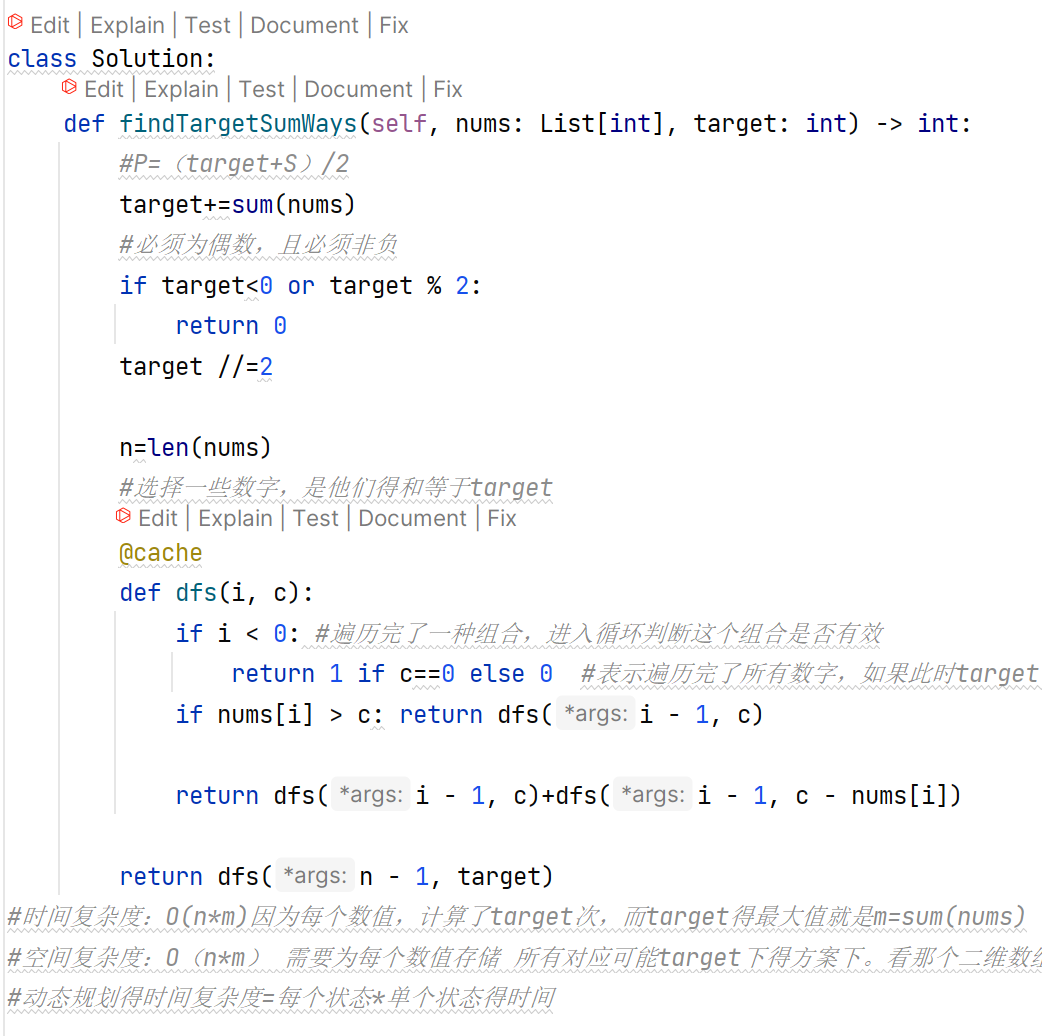
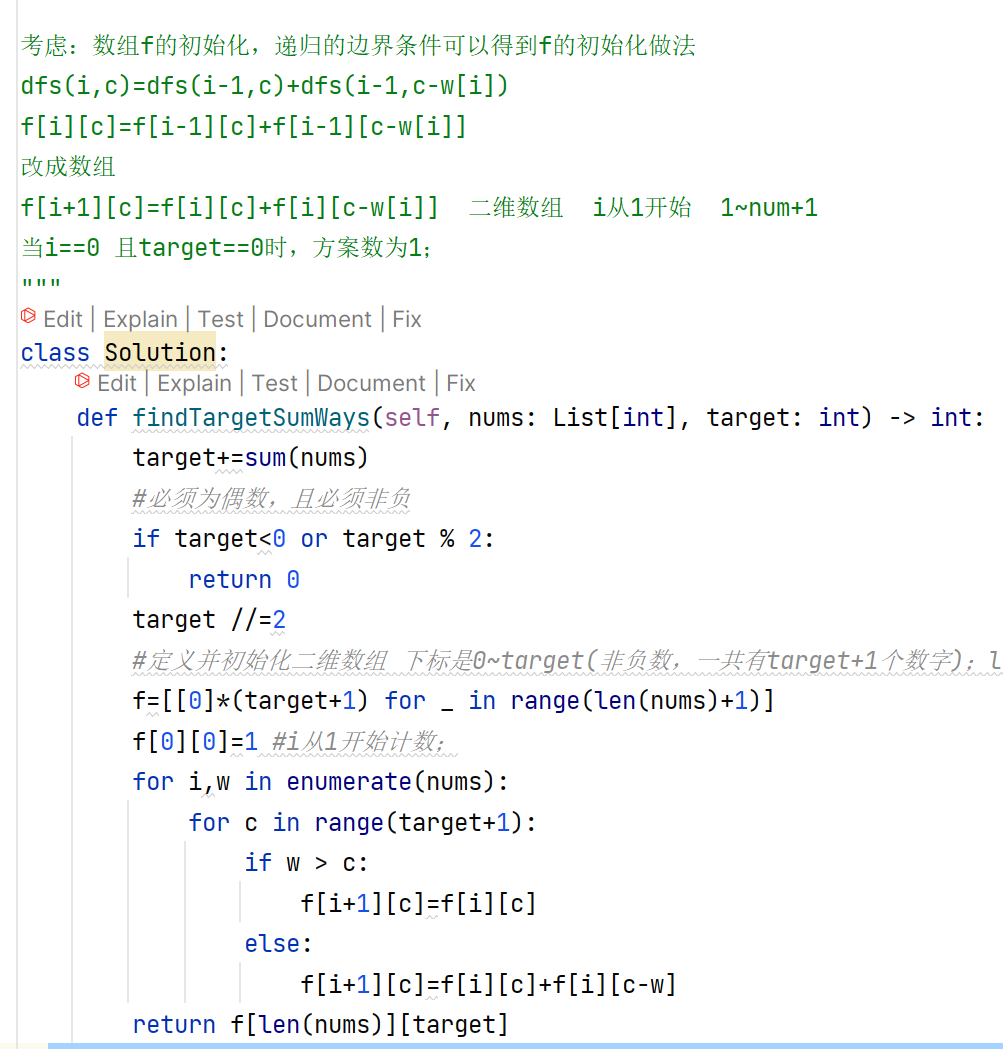
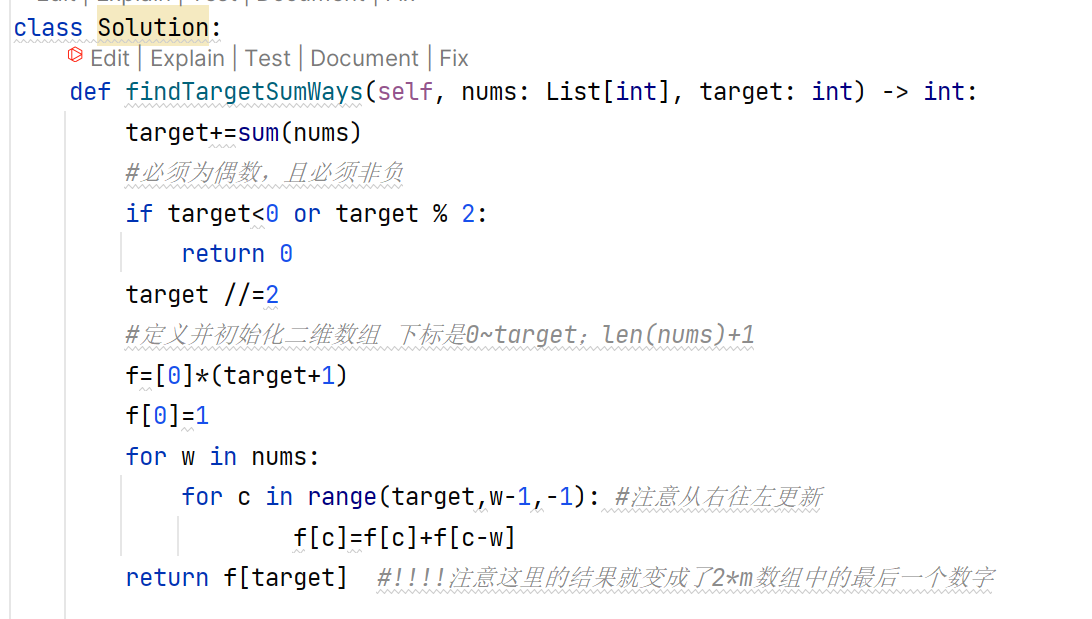
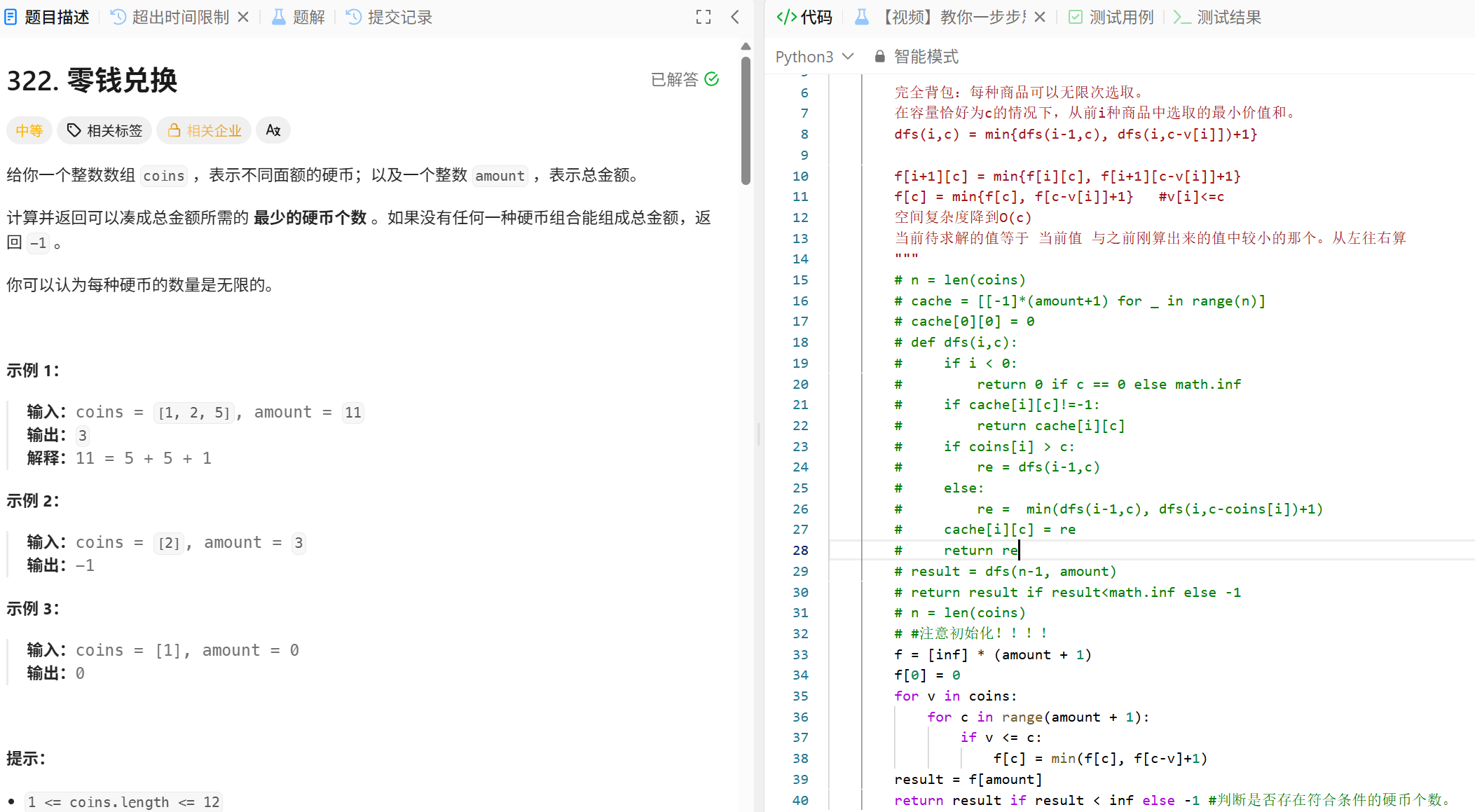
二分查找

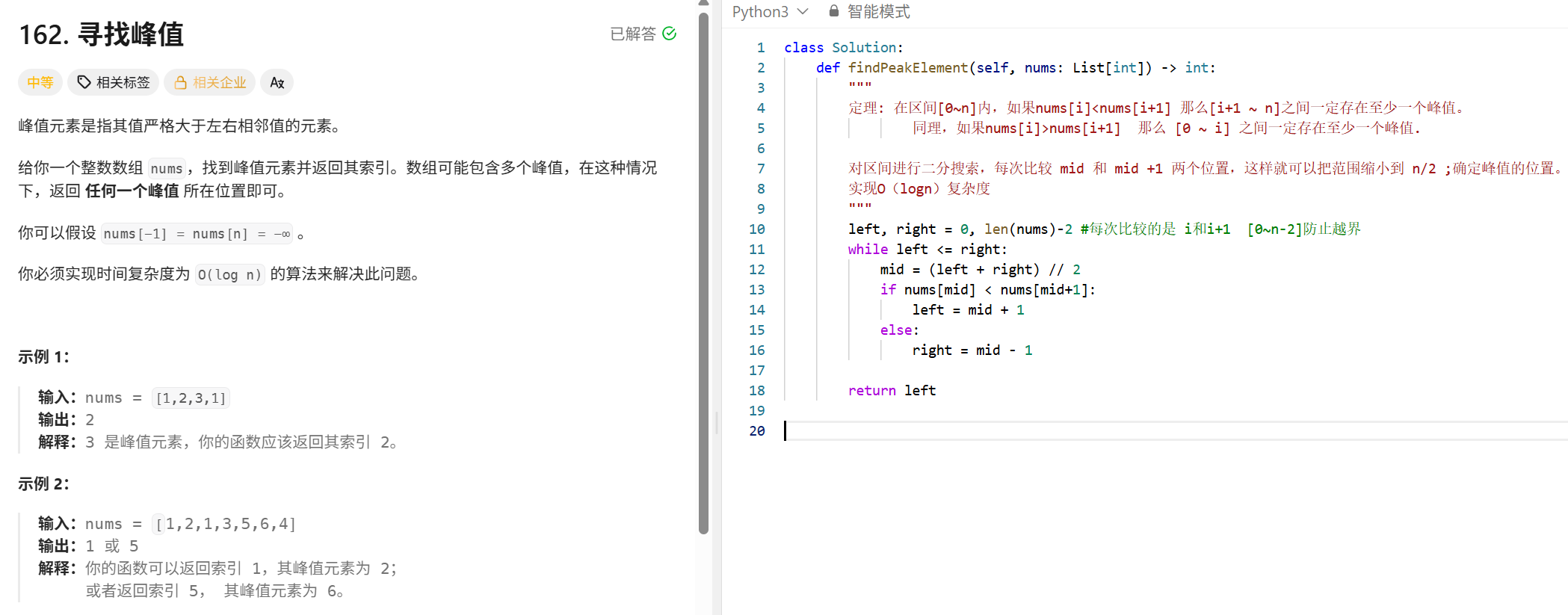
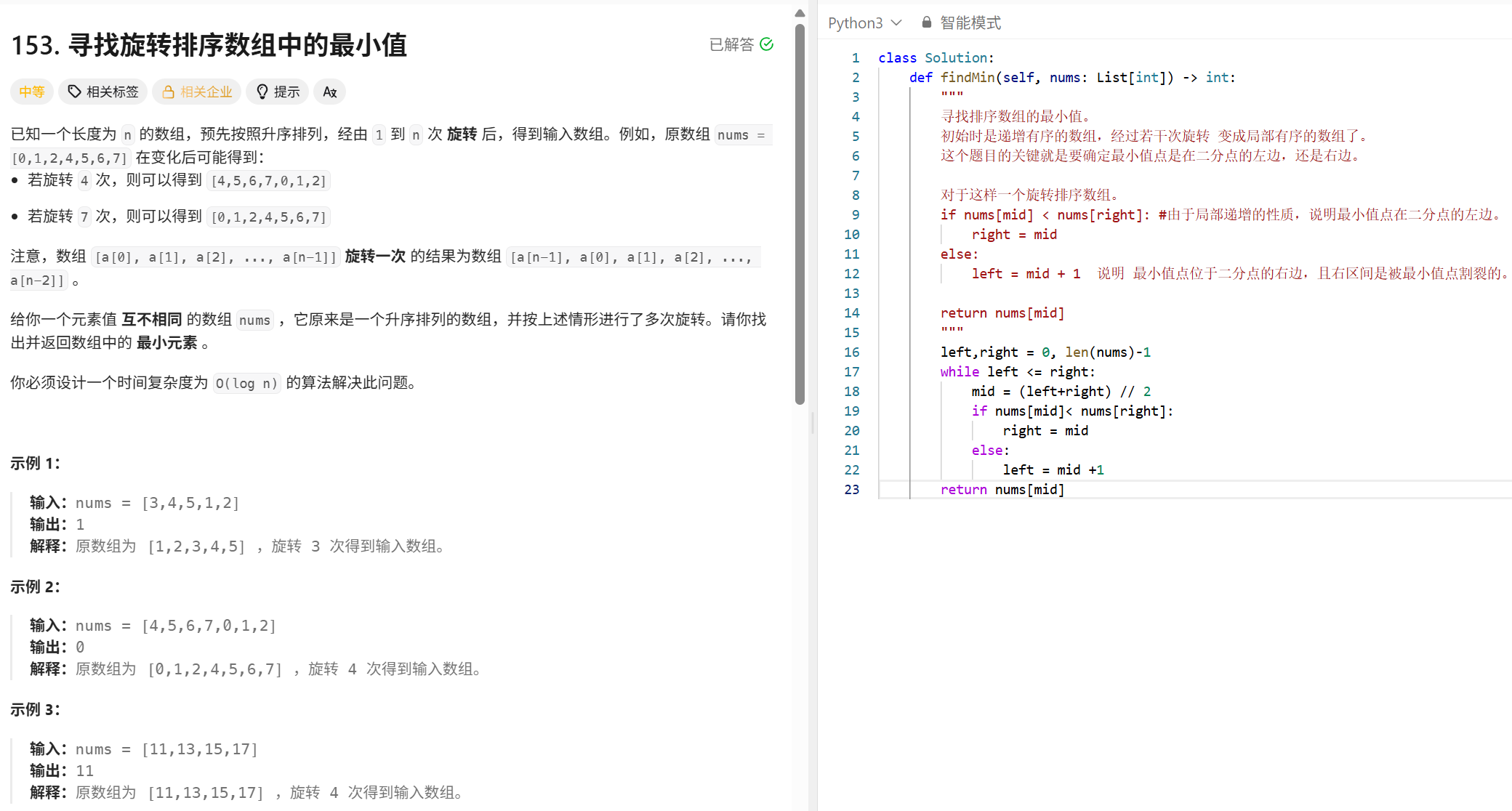
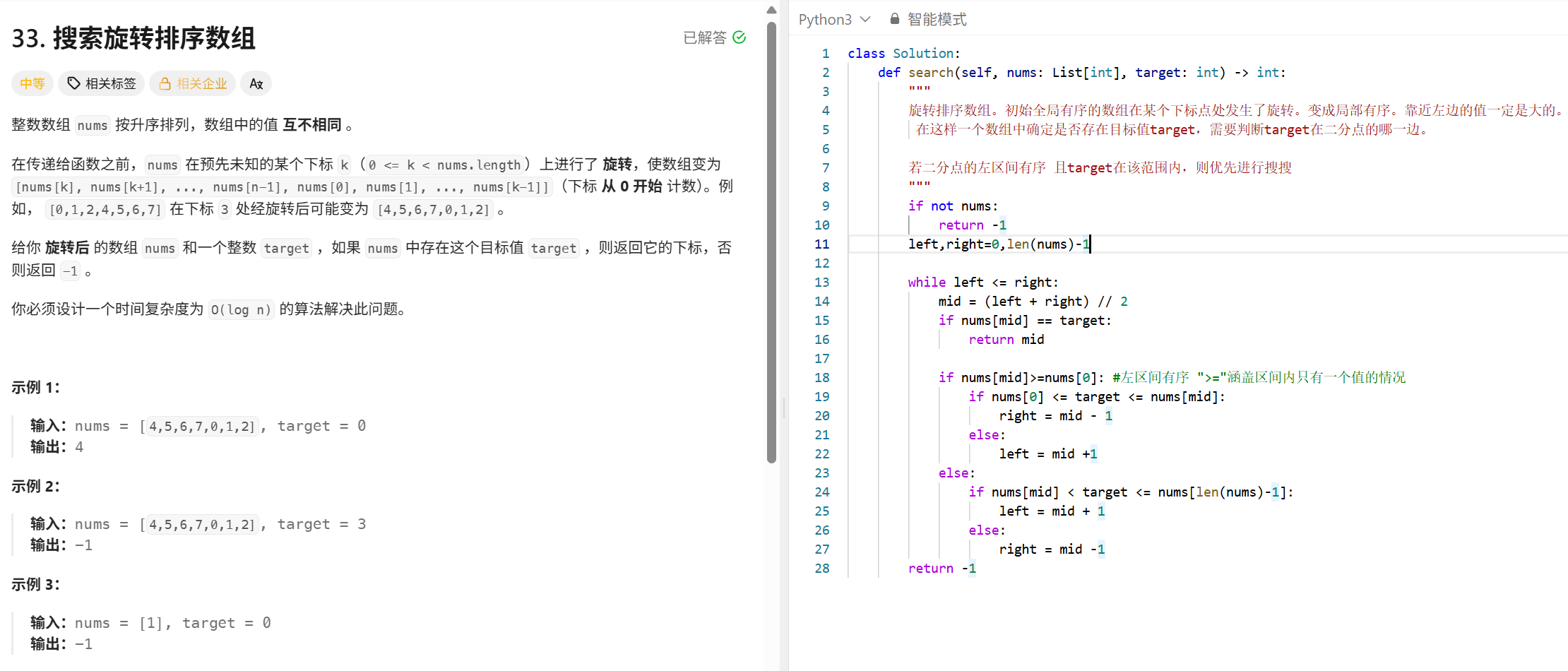
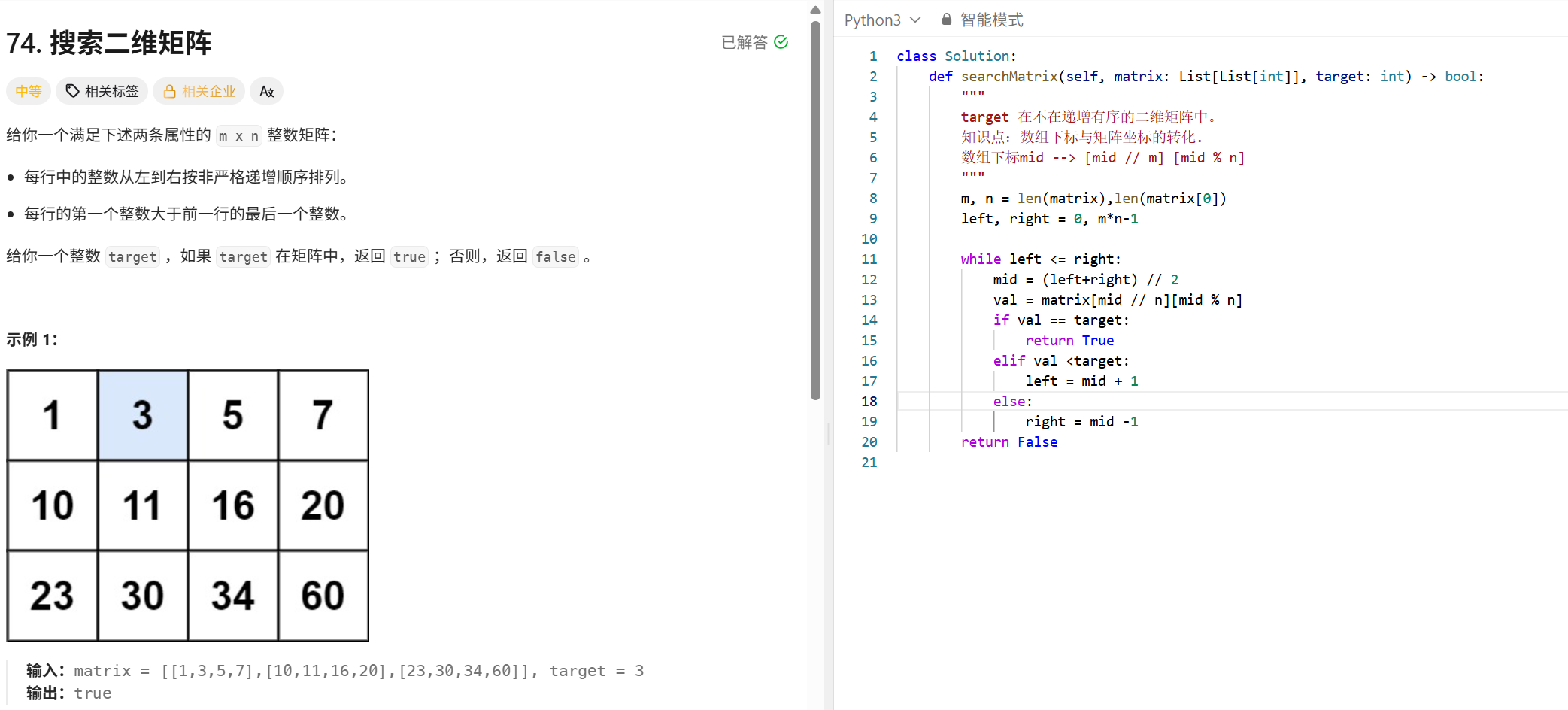
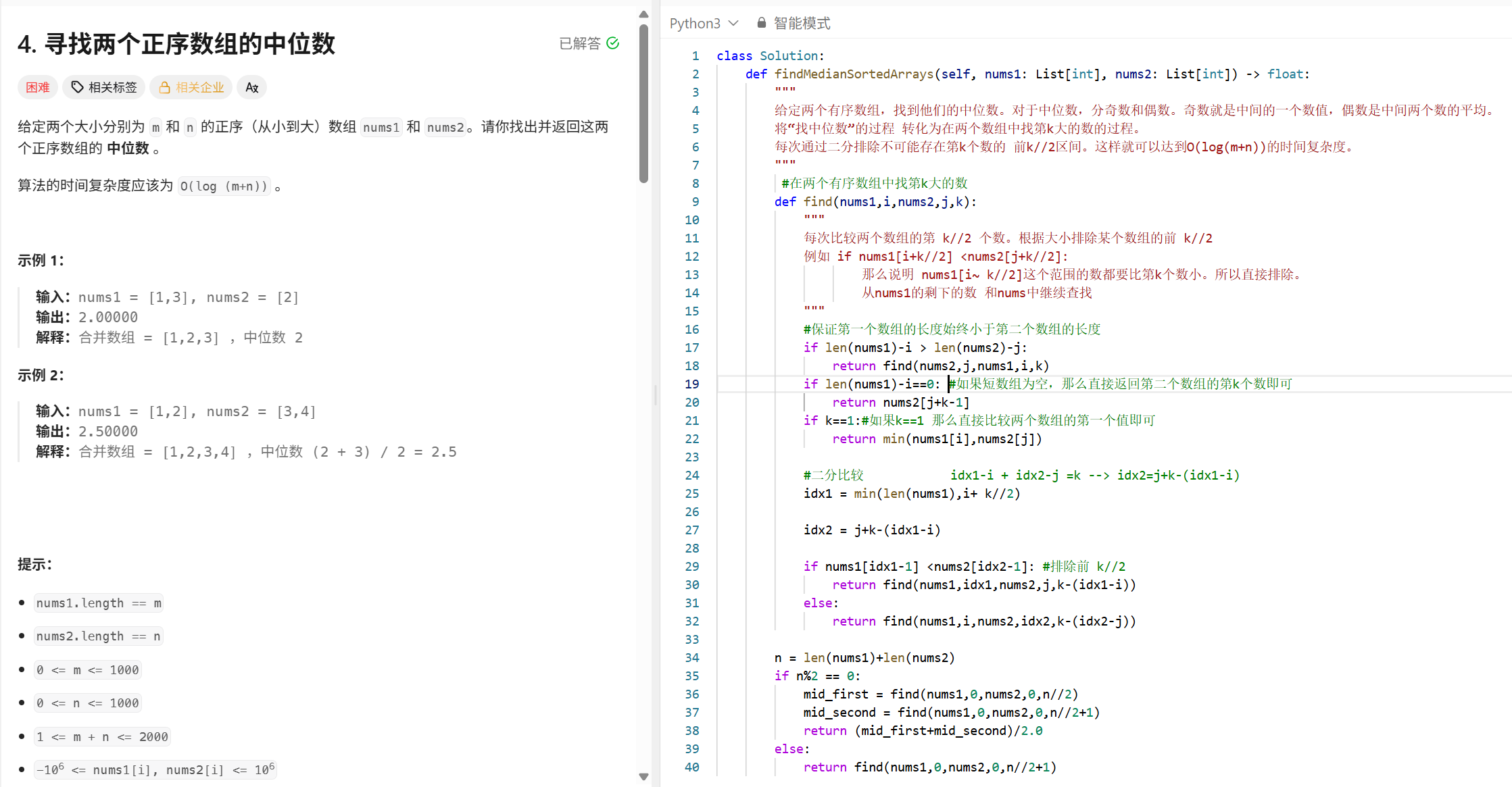
这个代码更规范
        def findKth(nums1, i, nums2, j, k):
            # 保证 nums1 是更短的数组，减少越界可能
            if len(nums1) - i > len(nums2) - j:
                return findKth(nums2, j, nums1, i, k)

            # 如果 nums1 剩余为空，直接返回 nums2 的第 k 个数
            if i >= len(nums1):
                return nums2[j + k - 1]

            # 如果 k == 1，返回两个当前元素的最小值
            if k == 1:
                return min(nums1[i], nums2[j])

            # 尝试从 nums1 和 nums2 中各取 k//2 个元素来比较
            idx1 = i + min(len(nums1) - i, k // 2)
            idx2 = j + (k - (idx1 - i))  # 保证总共取了 k 个元素

            val1 = nums1[idx1 - 1]
            val2 = nums2[idx2 - 1]

            if val1 < val2:
                # 舍弃 nums1[i:idx1]
                return findKth(nums1, idx1, nums2, j, k - (idx1 - i))
            else:
                # 舍弃 nums2[j:idx2]
                return findKth(nums1, i, nums2, idx2, k - (idx2 - j))

        n = len(nums1) + len(nums2)
        if n % 2 == 0:
            left = findKth(nums1, 0, nums2, 0, n // 2)
            right = findKth(nums1, 0, nums2, 0, n // 2 + 1)
            return (left + right) / 2.0
        else:
            return findKth(nums1, 0, nums2, 0, n // 2 + 1)

排序

冒泡：

"""
冒泡排序：每一趟将最大值或者最小值排到数组的末尾。
一共有n个元素，所以需要进行n躺排序。
每一趟需要从头都n-1-i个元素，相互比较
"""
def bubble_sort_optimized(nums: List[int]) -> List[int]:
    n = len(nums)
    for i in range(n):
        swapped = False  # 标志变量，记录是否发生了交换
        for j in range(0, n - i - 1):
            if nums[j] > nums[j + 1]:
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
                swapped = True  # 发生了交换
        if not swapped:  # 如果没有发生交换，说明数组已经有序
            break
    return nums

归并：

"""
归并排序是一种分治的思想，将大问题拆解为小问题。
分解：通过递归的方法对数组从中间进行划分，直到数组长度为1。 O(logn)
合并：对两个有序子数组进行合并，合并为一个新的数组。O(n)

总的时间复杂度：O(nlogn)
空间复杂度:O(n) 开辟一个新数组来存储合并好的有序数组。
"""
def merge_sort(nums:List[int]) -> List[int]:
    if len(nums) <= 1:
        return nums

    mid =  len(nums) // 2
    left_nums = merge_sort(nums[:mid])
    right_nums = merge_sort(nums[mid:])

    return merge(left_nums,right_nums)

def merge(left_nums:List[int], right_nums:List[int]) -> List[int]:
    result = []
    i = j = 0

    while i < len(left_nums) and j < len(right_nums):
        if left_nums[i] < right_nums[j]:
            result.append(left_nums[i])
            i += 1
        else:
            result.append(right_nums[j])
            j +=1

    #把剩余元素extend到目标数组中
    result.extend(left_nums[i:])
    result.extend(right_nums[j:])

    return result

快速排序：

"""
快速排序：
也是一种分治思想，将一个数组的排序，通过partition划分操作，分解成两部分，分别对左右子数组进行排序直至整体有序。
partition的具体操作：
从数组中随机选取一个枢纽元素pivot，进行遍历，将小于pivot的元素全部放到pivot的左边，大于pivot的元素放到右边。
这样一趟划分之后，pivot元素将数组划分成左右两部分，然后分别对pivot的左右两部分进行快排（所以参数需要传入一个待排序的范围）即可。

一次partition会确定一个元素的位置，n个元素时间复杂度O(n)
当每次划分尽可能平均的时候，总时间复杂度为O(nlogn),否则 最坏时间复杂复杂度为O(n^2)
"""

def partition(nums: List[int], low: int, high: int) -> int:
    i = low
    j = high
    pivot = nums[low]

    while i < j:
        while i < j and nums[i] <=pivot:
            i +=1
        while i < j and nums[j] >=pivot:
            j -=1
        nums[i], nums[j] = nums[j], nums[i]
    #最终i = j 就是pivot的位置
    nums[i], nums[low] = pivot, nums[i]
    return i


def randompartition(nums: List[int], low: int, high: int) ->int:
    pivot_index = random.randint(low, high)
    nums[low], nums[pivot_index] = nums[pivot_index], nums[low]

    return partition(nums, low ,high)

def quicksort(nums: List[int], low, high) -> List[int]:

    if low < high:
        pivot_index = randompartition(nums, low, high)

        quicksort(nums, low, pivot_index - 1)
        quicksort(nums, pivot_index + 1, high)

    return nums
"""
优化：每次确定一个位置。上述的写法，当面对数组中全是相同元素的时候，会出现大量的重复操作，时间复杂度高。
下面的写法，一次可以确定若干相同的pivot的位置。
"""

def quict_sort(nums):
    if len(nums) <= 1:
        return nums
    random_index =random.randint(0,len(nums)-1)
    pivot = nums[random_index]
    left_nums = [x for x in nums if x < pivot]
    mid_nums = [x for x in nums if x == pivot]
    right_nums = [x for x in nums if x > pivot]
    return quict_sort(left_nums) + mid_nums + quict_sort(right_nums) 

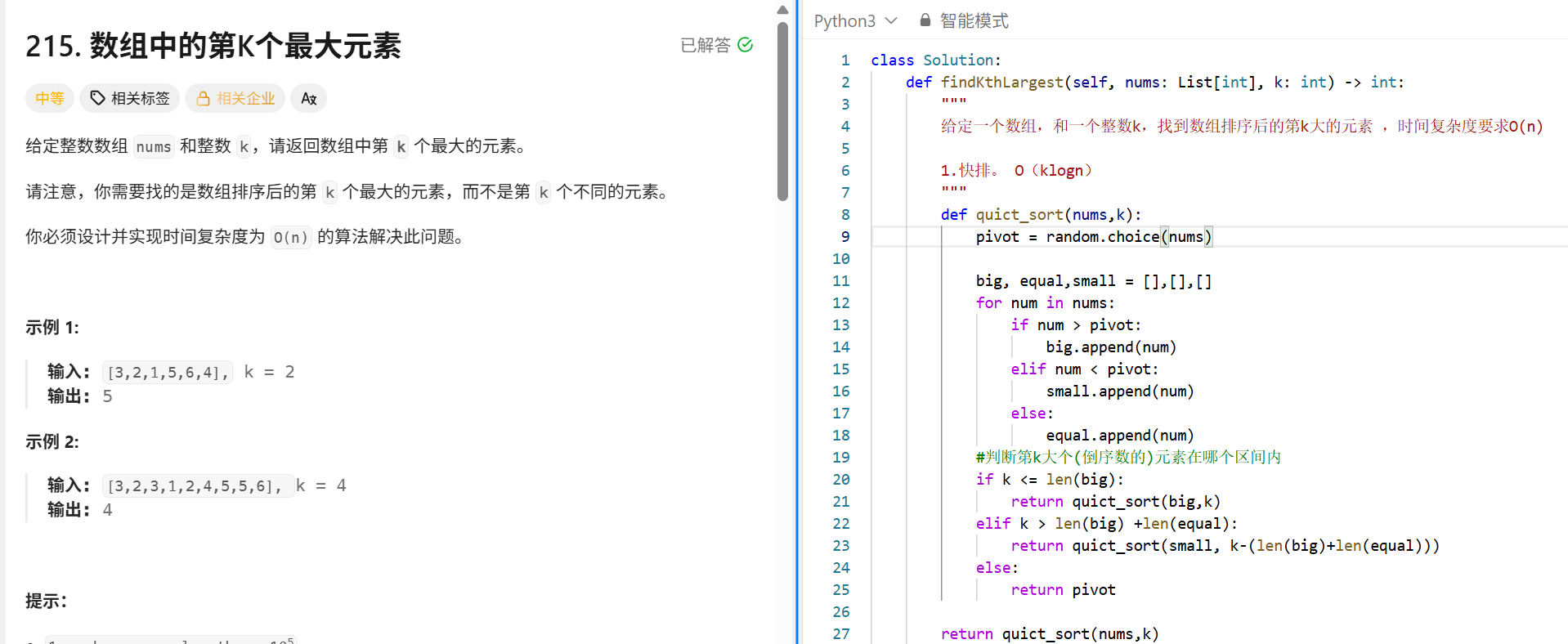
堆排序
堆是一种可以在 O(log n) 时间内获取最小值的数据结构。

"""
堆排序：
大根堆：任意节点 >= 其子节点
小根堆：任意节点 <= 其子节点

大根堆只能确定最大值，小根堆只能确定最小值。

创建初始堆：将数组进行顺序排序，从最后一个非叶子节点((n-2)//2)倒序调整。
    调整：将当前节点与其子节点进行比较，逐渐下调，创建性质要求的大/小根堆。
将初始堆的根节点与最后一个节点进行交换；并进行排序重建堆(将剩余节点重新调整为大/小根堆)
时间复杂度 ：建堆 O(n); 下调：O(logn)  排序重建堆的时间复杂度O(nlogn)

(i-1)//2
i
2*i+1  2*i+2
"""
#注意最后一个非叶子节点的索引：(n-2)//2 或者 n//2-1


class MaxHeap:
    # def __init__(self):
    #     self.max_heap=[]
    def __buildMaxHeap(self,nums):
        #将数组元素存储到顺序存储结构当中
        # for i in nums:
        #     self.max_heap.append(i)
        n=len(nums)
        #从最后一个非叶子节点倒叙调整为大根堆
        for i in range((n-2)//2,-1,-1):
            self.__shiftdown(i,n,nums)
    def maxHeapSort(self,nums:[int])->[int]:
        #创建初始的大根堆
        self.__buildMaxHeap(nums)
        #根节点和最后一个节点交换，从根节点开始逐步下调使得剩下的i-1个节点符合大根堆
        for i in range(len(nums)-1,-1,-1):
            nums[0],nums[i]=nums[i],nums[0]
            self.__shiftdown(0,i,nums)#这里的i刚好是去除最后一个元素之后剩下元素的个数n。
        #返回调整好的数组
        return nums
    #逐步下调
    def __shiftdown(self,i,n,nums):
        #逐渐下调，直到底层
        while 2*i+1<n:
            left,right=2*i+1,2*i+2
            #找到较大的子节点
            if right>=n:
                #只有左节点
                larger=left
            else:
                larger=left if nums[left]>nums[right] else right
            #若当前元素小于最大的子节点，则交换
            if nums[i]<nums[larger]:
                nums[i],nums[larger]=nums[larger],nums[i]
                i=larger
            else:
                break
class Solution:
    def maxHeapSort(self,nums)->[int]:
        return MaxHeap().maxHeapSort(nums)
    def sortArray(self, nums: List[int]) -> List[int]:
        #给定一个数组进行大根堆排序（从小到大进行排序）
        return self.maxHeapSort(nums)
#分析：初始建堆的过程是O(n)；下调的最大深度是树的高度O（logn）;总时间复杂度是O(nlogn)

class MinHeap:
    def __init__(self):
        self.minheap = []
    
    def __len__(self):
        return len(self.minheap)

    "向堆中添加元素：添加到元素的末尾，然后从末尾开始逐渐上调，调整为堆"
    def push(self,val):
        self.minheap.append(val)
        self.__shift_up(len(self.minheap)-1)

    def __shift_up(self,i):
        #从末尾元素开始逐渐与夫节点比较大小，上调
        while ((i-1)//2) >= 0 and self.minheap[(i-1)//2] > self.minheap[i]:
            self.minheap[(i-1)//2],self.minheap[i] = self.minheap[i], self.minheap[(i-1)//2]
            i = (i-1)//2 
    
    "向堆中删除元素，将堆顶元素和最后一个元素交换，删除最后一个元素。然后从根节点开始下调"
    def pop(self):
        if not self.minheap:
            return None
        self.minheap[0], self.minheap[-1] = self.minheap[-1], self.minheap[0]
        val = self.minheap.pop()

        self.__shift_down(0,len(self.minheap))

        return val

    def __shift_down(self,i,n):
        while 2*i+1 < n:
            left,right = 2*i+1, 2*i+2
            if right >= n:
                smallest = left
            else:
                smallest = left if self.minheap[left]<self.minheap[right] else right

            if self.minheap[smallest] < self.minheap[i]:
                self.minheap[smallest],self.minheap[i] = self.minheap[i], self.minheap[smallest]
                i = smallest
            else:
                break

class Solution:
    def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:
        """
        给两个数组，和一个整数k。
        要求从这两个数组组成的所有数对中按照和从小到大排序，返回和最小的k个数对。

        方法:使用堆完成一次O(logn)的查找。
        初始时将元素((nums1[i]+nums[0], i, 0)) 将nums1的前k个元素和nums2的第一个元素存入到堆中，建立最小堆。

        然后从建立的最小堆中依次取出和最小的数对。然后将候选(i,j+1)继续存入到堆中，直到取出前k个值.
        
        这里涉及到堆的push操作和pop操作
        """
        if not nums1 or not nums2 or k == 0:
            return []

        minheap = MinHeap()
        result =[]

        #将nums1的前k个数 和nums2的第一个数 push到堆中.
        for i in range(min(k, len(nums1))):
            minheap.push((nums1[i]+nums2[0], i, 0))
        
        #每次O(logn)的时间复杂度取出最小和的数对
        while len(result) < k and len(minheap) >0:
            small_sum, i, j = minheap.pop()
            result.append([nums1[i], nums2[j]])
            
            if j+1 < len(nums2):
                minheap.push((nums1[i]+nums2[j+1], i, j+1))
        
        return result 
       

"""
对于一个有序列表，如果长度为奇数，那么中位数就是中间的那一个值；(12 3 45 -->3)
如果长度是偶数，那么中位数就是中间两个值的平均. （1 2 3 4 -->(3+4)/2）

findMedian实时找中位数：维护两个堆。
大根堆存储数据流的左半边。
小根堆存储数据流的右半边。
两个堆的元素个数相差<=1

这样 偶数：大小根堆堆顶元素的平均。
奇数：大根堆的堆顶。

addNum;实时添加数据:
若当前值 >= 大根堆的堆顶尝试放到左半部分，否则放到右半部分。
然后通过堆顶实时保持两个堆中元素个数平衡。
"""
"""
面试话术：找中位数，需要根据奇偶性判断，奇数，就是中间的一个值。
偶数就是中间两个值的平均.
那么这个题，可以维护两个堆，一个大根堆存储左半部分，小根堆存储右半部分，两个堆的元素相差不超过1.
这样子，就可以根据堆顶实现O(1)实时计算中位数。
对于插入操作：小于中位数就插入左边，大于中位数就插入右边。然后通过转移堆顶元素保持堆的平衡。
"""
class Heap:
    def __init__(self,compare):
        self.data = []
        self.compare = compare #定义大/小根堆的调整规则

    def __len__(self):
        return len(self.data)

    def peak(self):
        return self.data[0] if self.data else None

    def push(self,val):
        self.data.append(val)
        self.__shift_up(len(self.data)-1)

    def pop(self):
        if not self.data:
            return None
        #交换堆顶和末尾元素，然后从堆顶下调
        self.data[0],self.data[-1] = self.data[-1],self.data[0]
        val = self.data.pop()

        if self.data:
            self.__shift_down(0)
            
        return val
    
    def __shift_up(self,i):
        parent_idx = (i-1)//2
        while parent_idx >=0 and self.compare(self.data[i],self.data[parent_idx]): #大根堆, parent > i
            self.data[parent_idx], self.data[i] = self.data[i],self.data[parent_idx]
            i = parent_idx
            parent_idx = (i - 1) // 2

    def __shift_down(self,i):
        n = len(self.data)
        while 2*i+1 < n:
            left, right = 2*i+1, 2*i+2
            if right >= n:
                larger = left
            else:
                larger = left if self.compare(self.data[left],self.data[right]) else right #如果是大根堆 取大的

            if self.compare(self.data[larger],self.data[i]):
                self.data[larger],self.data[i] = self.data[i], self.data[larger]
                i = larger
            else:
                break

class MedianFinder:
    def __init__(self):
        #初始化两个大小根堆
        "因为大小根堆的上调/下调的规则不一样,可以通过传入一个lambda函数来区分大小根堆"
        #大根堆，节点大于等于任意子节点
        #小根堆，节点小于等于任意子节点
        self.left = Heap(lambda a, b: a>b)
        self.right = Heap(lambda a, b:a<b)

    def addNum(self,num:int)->None:
        #根据当前元素与中位数的大小尝试插入
        if len(self.left) == 0 or num <= self.left.peak():
            self.left.push(num)
        else:
            self.right.push(num)

        #通过转移堆顶，保持大小堆中元素的平衡
        if len(self.left) > len(self.right) + 1:
            self.right.push(self.left.pop())
        elif len(self.right) > len(self.left) + 1:
            self.left.push(self.right.pop())

    def findMedian(self)->float:
        #根据奇偶性 决定怎么计算
        #偶数 -->两个堆的长度相同
        if len(self.left) == len(self.right):
            if len(self.left) == 0:
                return 0.0
            else:
                return (self.left.peak()+self.right.peak())/2.0
        elif len(self.left) > len(self.right):
            return float(self.left.peak())
        else:
            return float(self.right.peak())

回溯

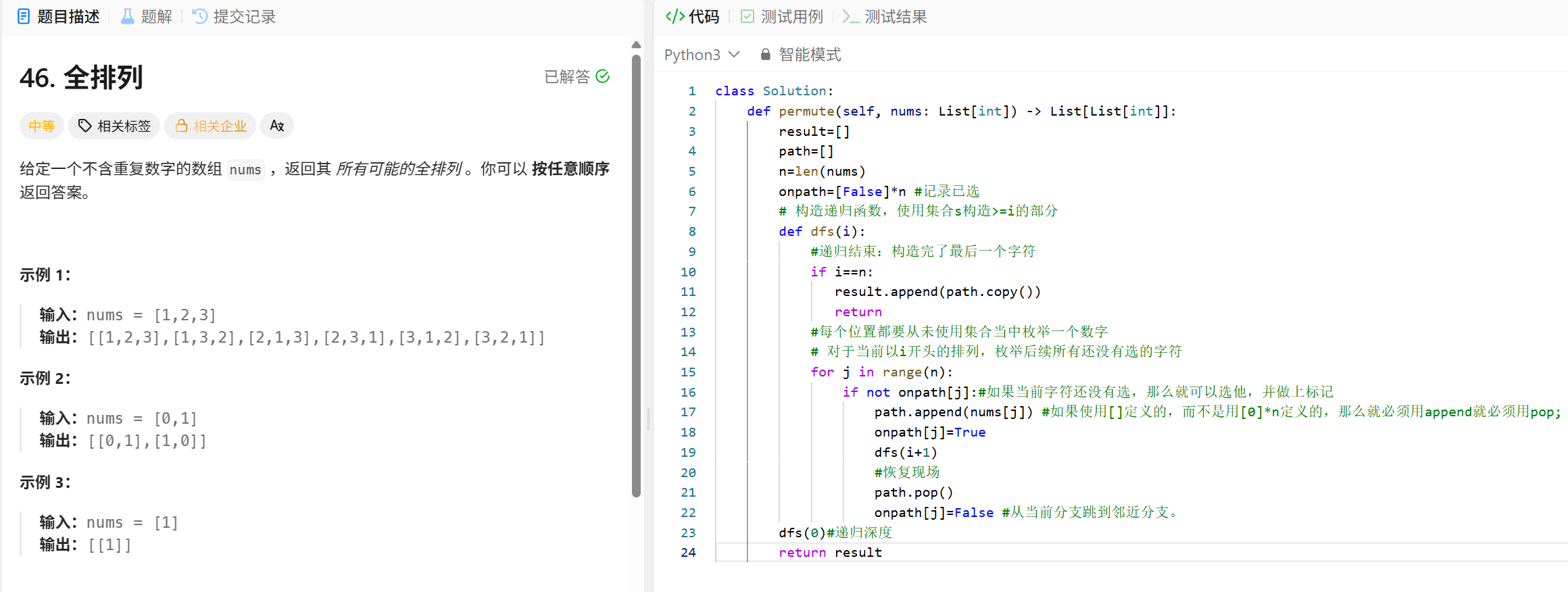
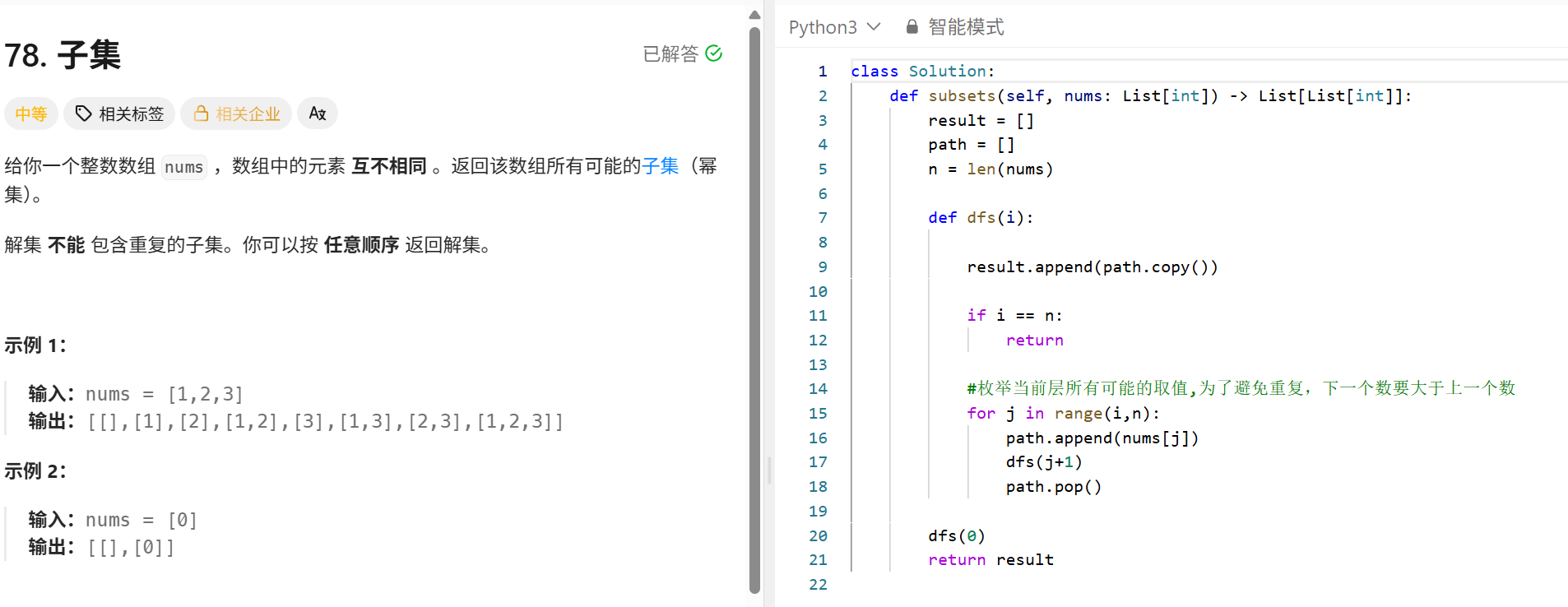
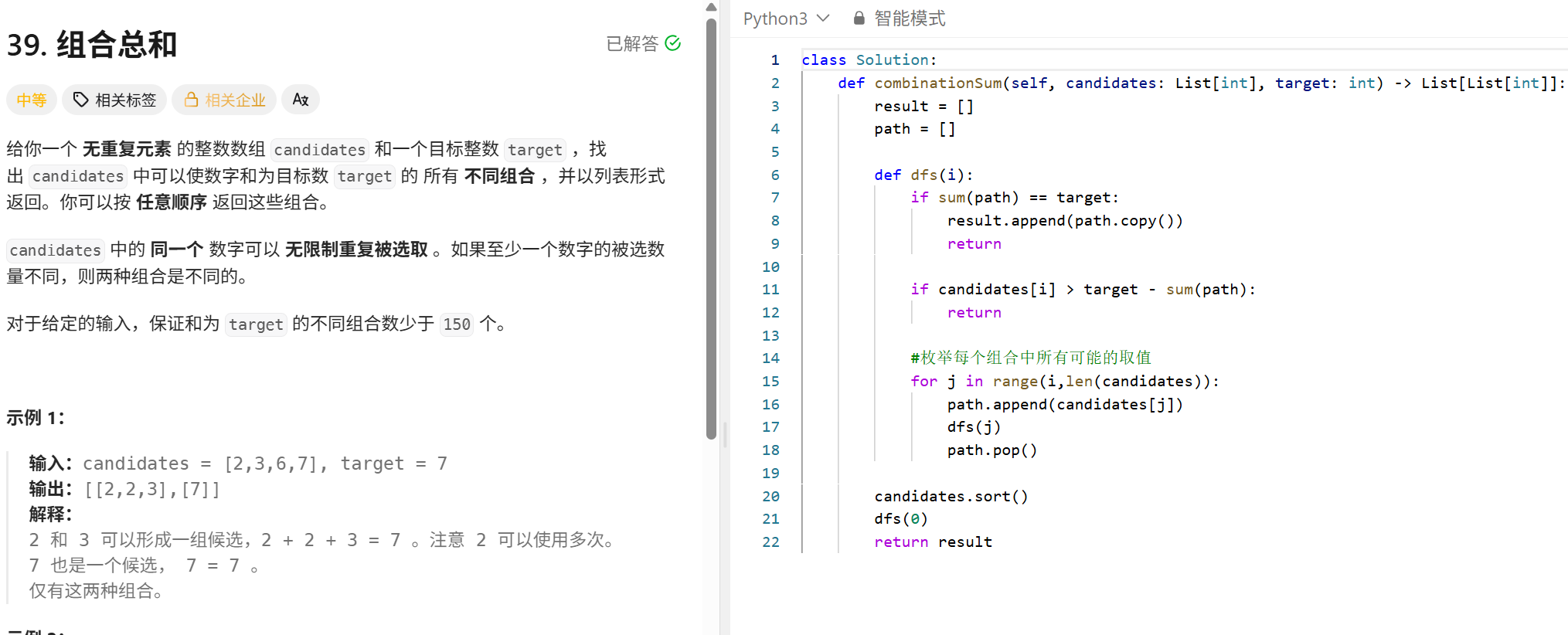
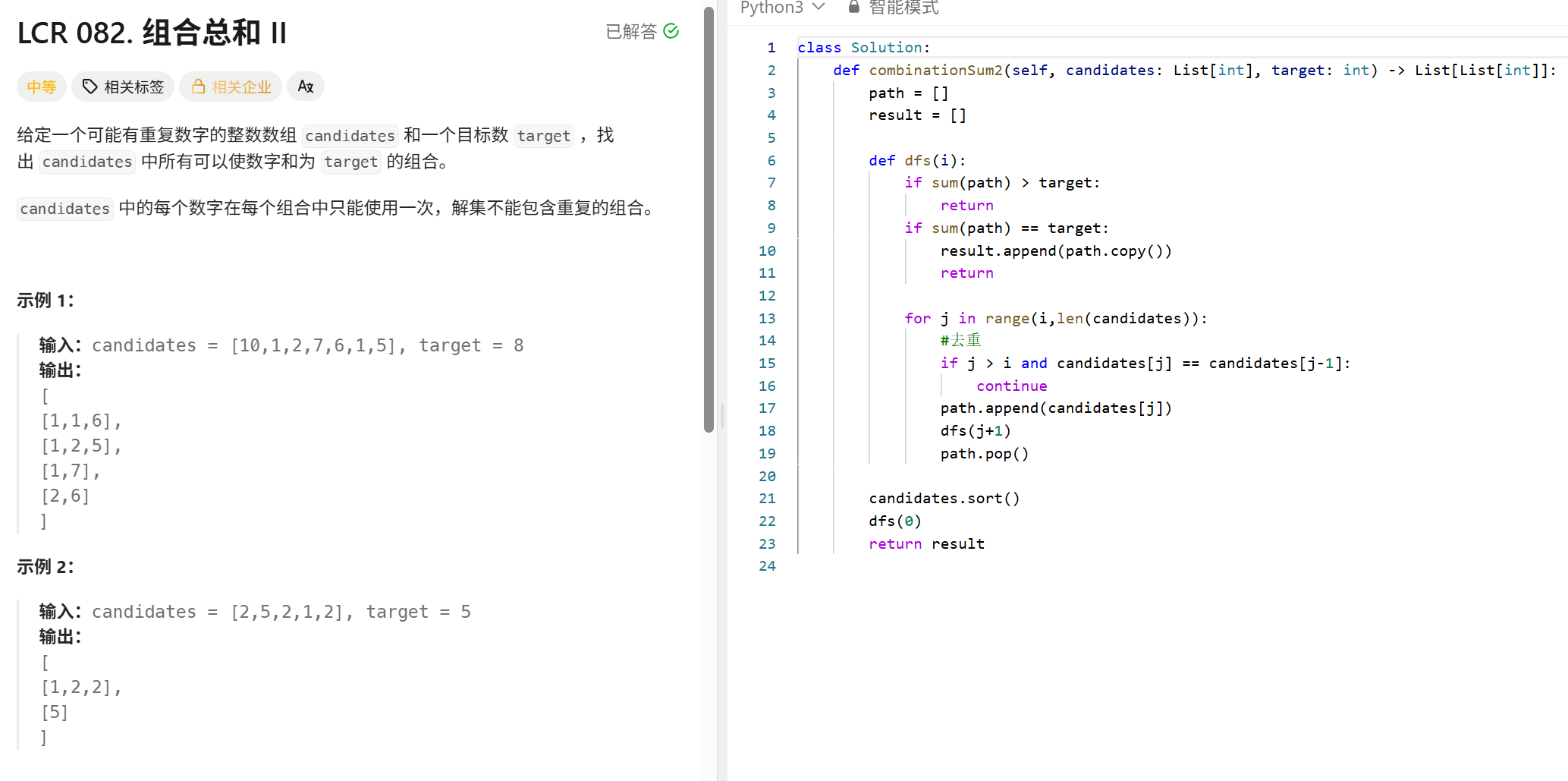
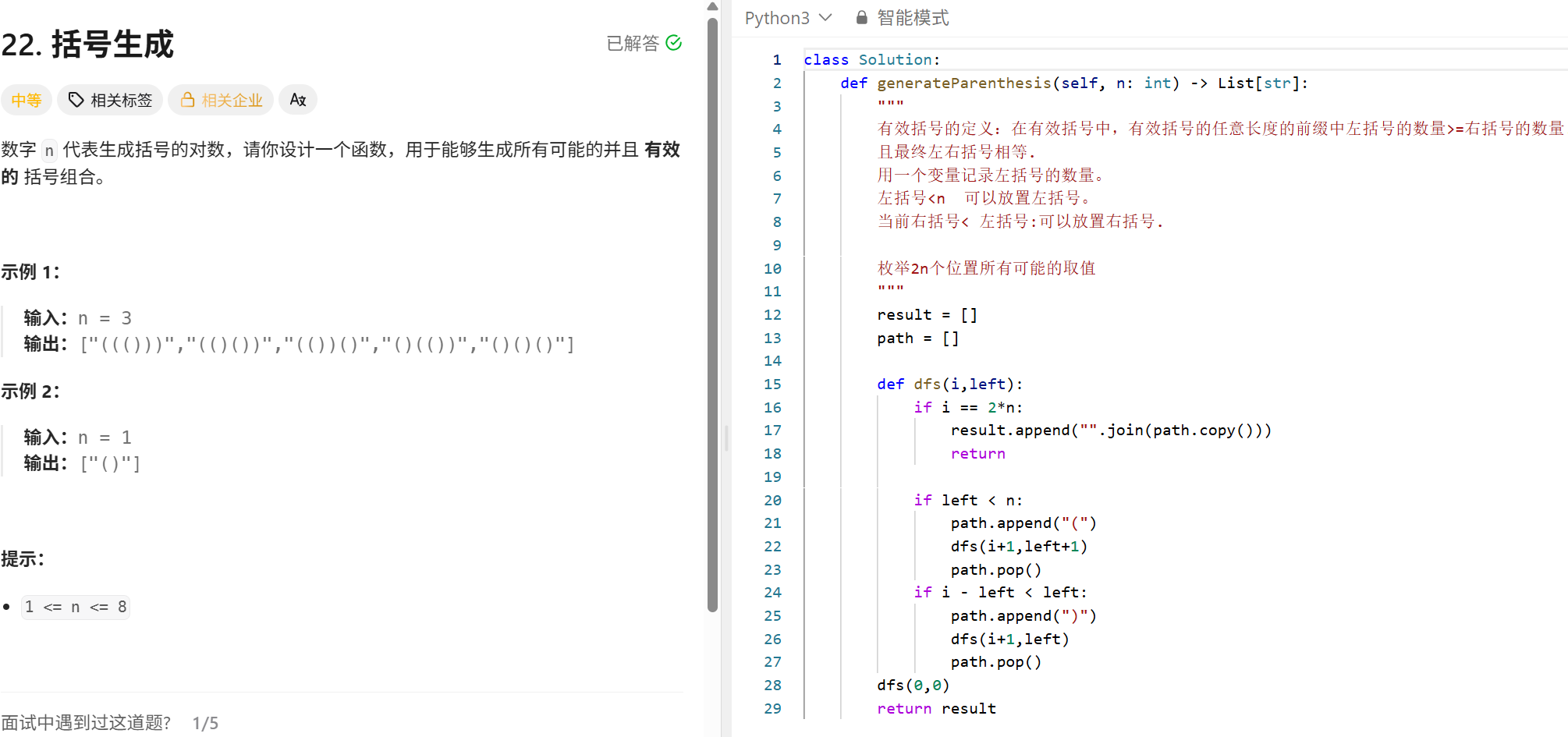
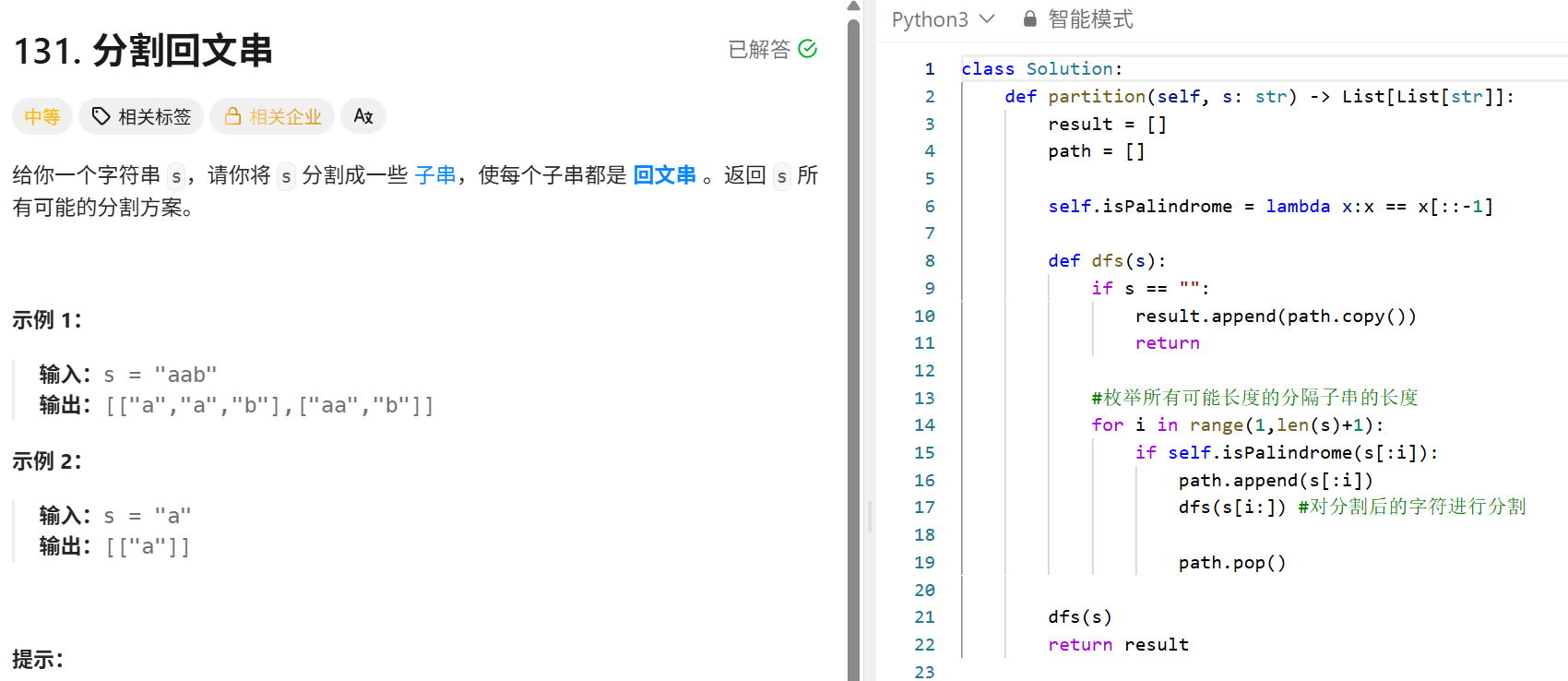
class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        """
        BFS 和DFS
        遍历网格中的每一个元素，如果当前元素是"1"说明找到了一个岛屿，result+1；将当前网格放入到队列中，
        循环队列不空：以当前网格(i,j)为岛屿的起点，进行上下左右四个方向搜索相邻的陆地，把他们都做上标记，并放到队列中。

        （result记录的是岛屿起点的数量. 有多少个不同的起点，就有多少岛屿
        """
        row,col = len(grid),len(grid[0])
        queue = collections.deque([])
        result = 0

        for i in range(row):
            for j in range(col):
                if grid[i][j] == "1":
                    result += 1
                    grid[i][j] = "0"
                    queue.append((i,j))

                    while queue:
                        r,c = queue.popleft()
                        #对其上下左右进行搜索
                        for x,y in [(r-1,c),(r+1,c),(r,c-1),(r,c+1)]:
                            if 0<= x<row and 0<= y <col and grid[x][y] == "1":
                                grid[x][y] = "0"
                                queue.append((x,y))
        return result
        #DFS
        row,col = len(grid),len(grid[0])
        result = 0

        def dfs(i,j): #以当前格子作为岛屿的起点进行上下左右的搜索
            if i<0 or j<0 or i>=row or j>=col or grid[i][j] == "0":
                return

            grid[i][j] = "0"
            #搜索相邻陆地
            dfs(i-1,j)
            dfs(i+1,j)
            dfs(i,j-1)
            dfs(i,j+1)
        
        for i in range(row):
            for j in range(col):
                if grid[i][j] == "1": #以当前格子为起点进行dfs搜索
                    result += 1
                    dfs(i,j)

        return result
    
    #ACM输入样例
    n = int(input())
    grid = [input().split() for _ in range(n)]

S=Solution()
print(S.numIslands(grid))

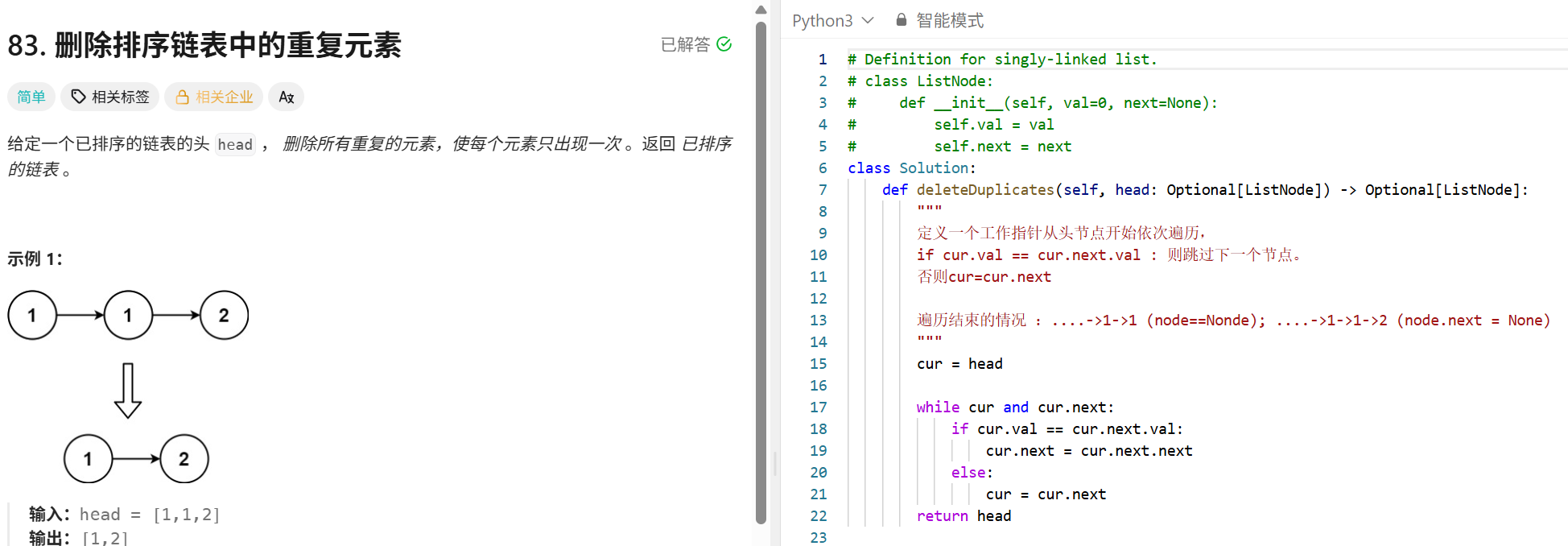
链表

"""
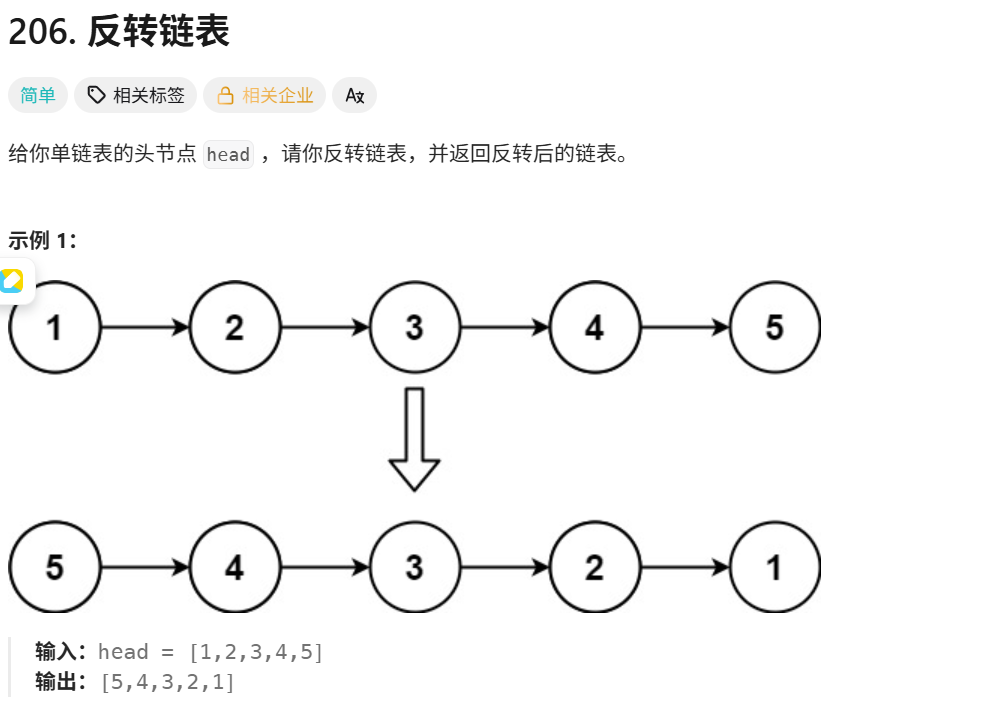
反转链表：
"""
class ListNode:
    def __init__(self,val=0,next=None):
        self.val = val
        self.next = next

class Solution:
    def reverseList(self,head:Optional[ListNode])->Optional[ListNode]:
        # """
        # 递归方法：
        # 1-->2-->3-->4
        # 递归一直递归到最后一个节点reversedhead，兵返回到倒数第二个节点head
        # head.next.next = head
        # head.next = None
        # """
        # #递归最后一个节点（head.next == None）就返回
        # if not head or not head.next:
        #     return head
        #
        # reversed_head = self.reverseList(head.next)
        # #当前是倒数第二个节点   1-->2-->3<--4
        # head.next.next = head
        # head.next = None
        # return reversed_head #一直不断的往前传递反转后的头节点,也就是最后一个节点 4

        "迭代的方法"
        """
        1-->2-->3-->4
        定义前驱指针pre=None  
        cur=head
        保存next next=cur.next
        cur.next = pre
        pre = cur
        cur = next
        """
        pre = None
        cur = head
        while cur:
            nxt = cur.next
            cur.next = pre
            pre = cur
            cur = nxt
        return pre #最后pre指向最后一个节点

"ACM格式构造输入链表"
def build_list(val:List[int]) -> Optional[ListNode]:
    dummy = ListNode(0)
    Cur = dummy
    for v in val:
        Cur.next = ListNode(v)
        Cur = Cur.next
    return dummy.next

#定义链表输出
def print_list(head:Optional[ListNode]) -> None:
    result = []
    while head:
        result.append(head.val)
        head = head.next
    print(result)

val = list(map(int,input().split()))
Linklist = build_list(val)
S=Solution()
head = S.reverseList(Linklist)
print_list(head)

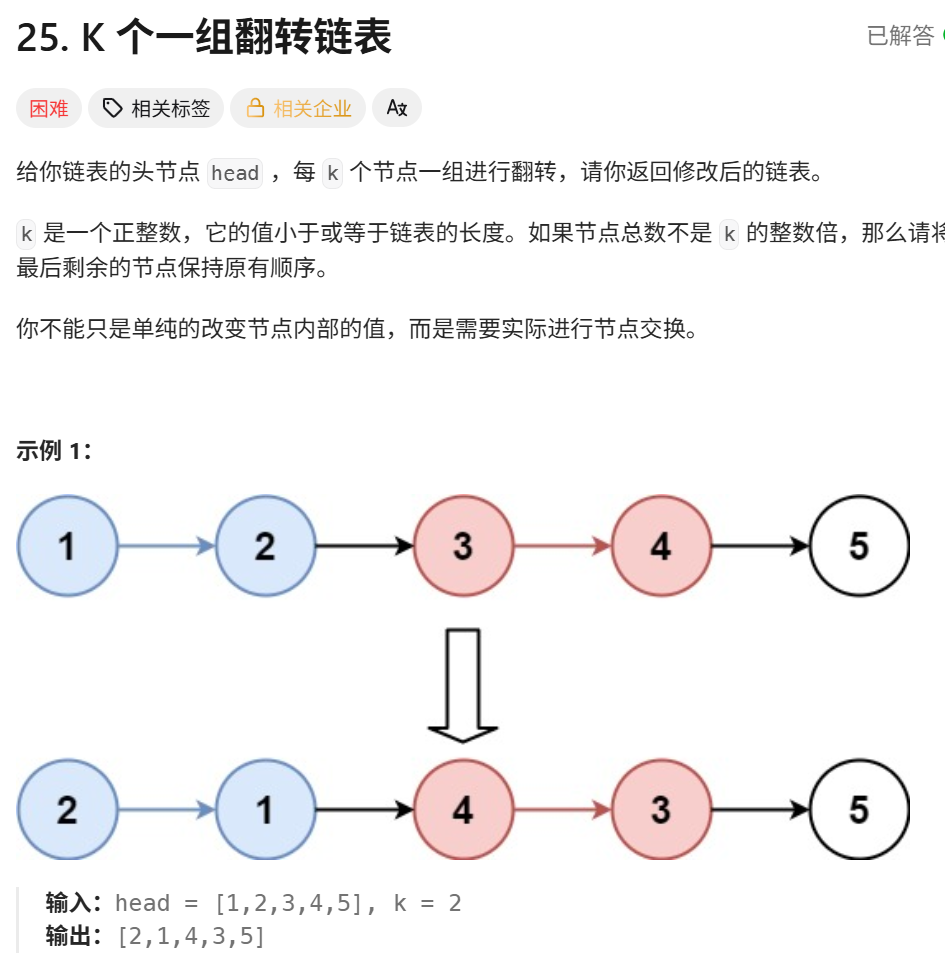
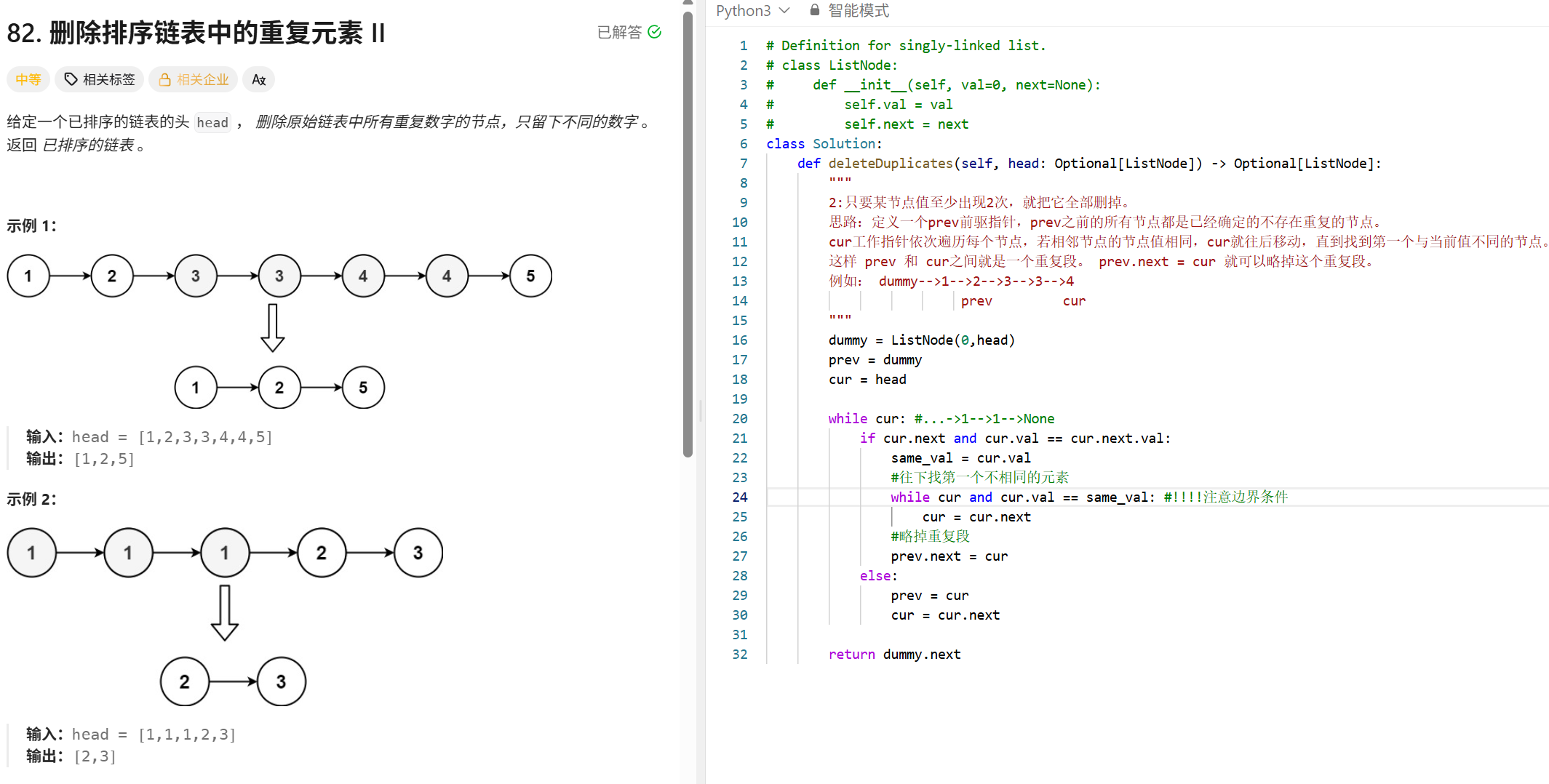
"K个一组反转链表"
class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def reverseKGroup(self, head: Optional[ListNode], k: int) -> Optional[ListNode]:
    """
    预先计算一个链表长度，每次K个一组进行反转。再
    每组开始之前要更新P0的位置，P0只向每组开始的前一个节点。
    当剩余长度不足k时，不再进行反转
    """
    n, cur, Pre = 0, head, None
    while cur:
        n += 1
        cur = cur.next

    # 每K个一组进行反转
    dummyhead = ListNode(0, next=head)  # 创建呀节点
    p0 = dummyhead
    cur = p0.next
    while n >= k:
        n -= k
        # 每K个一组进行反转
        for _ in range(k):
            nxt = cur.next
            cur.next = Pre
            Pre = cur
            cur = nxt
        # 小组反转完成之后要完成前后连接，但是！要注意保留p0后面的节点，因为需要更新P0
        # P0-->1-->2-->3-->4-->5
        # p0(dummy)-->1  4(Pre)-->3-->2-->1->None    5(Cur)
        # 保存下一个小组的前一个节点,刚好是当前p0的下一个节点，因为反转之后，就成了该节点就成了小组最后一个节点了
        p0_new = p0.next

        p0.next.next = cur
        p0.next = Pre  #把呀节点给放到开头
        p0 = p0_new
    return dummyhead.next

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

class MinHeap:
    def __init__(self):
        self.data = []

    def __len__(self):
        return len(self.data)
    
    def push(self,items):
        self.data.append(items)
        self.__shift_up(len(self.data)-1)

    def __shift_up(self,i):
        while (i-1)//2 >= 0 and (self.data[(i-1)//2][0] > self.data[i][0]):
            self.data[(i-1)//2], self.data[i] = self.data[i], self.data[(i-1)//2]
            i = (i-1) // 2

    def pop(self):
        #检查是否为空
        if not self.data:
            return None
        "将堆顶元素与最后一个元素互换，删除最后一个元素"
        self.data[-1],self.data[0] = self.data[0], self.data[-1]
        items = self.data.pop()

        #从根节点下调堆
        if self.data: #删除元素之后要判断是否为空
            self.__shift_down(0)

        return items

    def __shift_down(self,i): #从节点i开始下调
        #找出最小孩子节点
        n = len(self.data)
        while 2*i+1 < n:
            left,right = 2*i+1,2*i+2
            if right >= n:
                smaller = left
            else:
                smaller = left if self.data[left][0] < self.data[right][0] else right
            
            if self.data[i][0] > self.data[smaller][0]:
                self.data[i],self.data[smaller] = self.data[smaller],self.data[i]
                i = smaller
            else:
                break


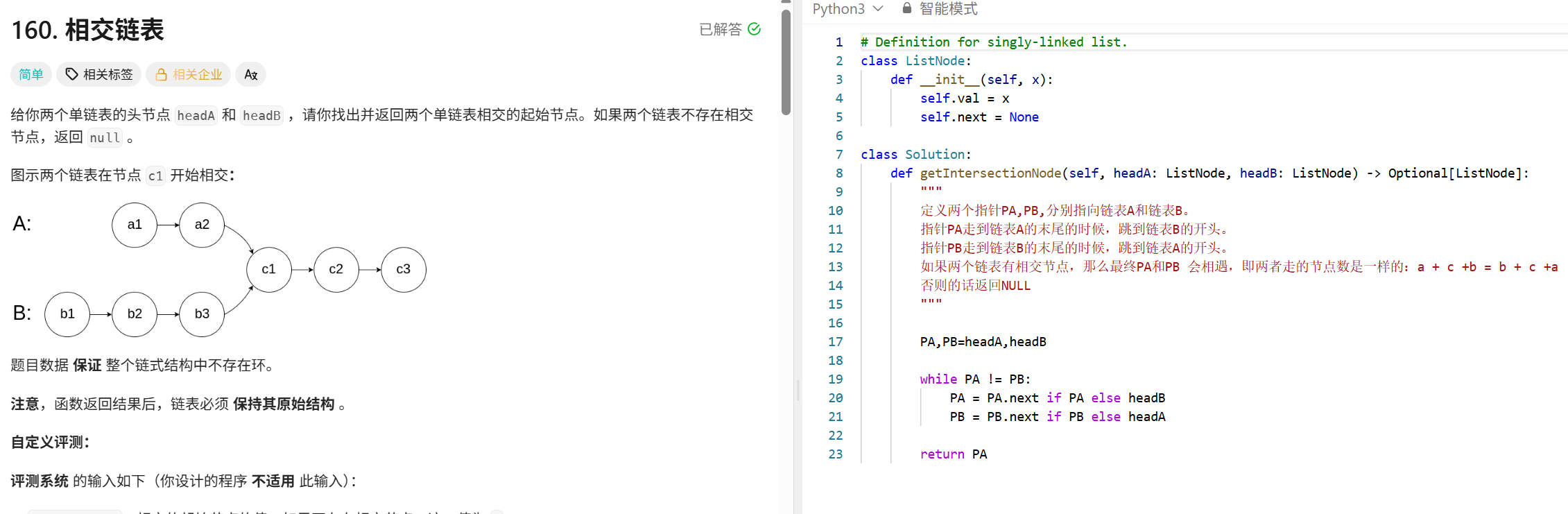
class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        """
        使用小根堆实现K个链表节点的排序。
        首先将数组链表的头节点放入到堆中，构建小根堆。
        取出堆顶元素加入到 合并链表中。
        若堆顶节点还有后续节点，则将其加入到堆中，重新构建小根堆排序。
        总的时间复杂度是O（nlogn）
        """
        minheap = MinHeap()
        #将头节点放入堆中，构建小根堆
        for i, node in enumerate(lists):
            if node: #lists = []
                minheap.push((node.val,node)) #堆中存放节点值和节点指针
        
        dummy = ListNode(0,None)
        cur = dummy

        #从堆中取出堆顶，加入到合并链表中。直到堆为空
        while len(minheap):
            val, node = minheap.pop()
            cur.next = node
            cur = cur.next

            if node.next:
                minheap.push((node.next.val,node.next))
        
        return dummy.next

def build_link_list(arr):
    dummy = ListNode()
    curr = dummy
    for x in arr:
        curr.next = ListNode(x)
        curr = curr.next
    return dummy.next
"""
ACM构造输入
"""
lists = []
n = int(input())
for i in range(n):
    node = input().split()
    if not node:
        lists.apped(node)
    else:
        node_list = list(map(int,node))
        lists.append(build_link_list(node_list))


# 检查构造结果（测试用）
for head in lists:
    vals = []
    while head:
        vals.append(head.val)
        head = head.next
    print(vals)

"""
双指针实现LRU策略，链头是最新访问过的。连尾是最久没有访问的。

LRU Cache的两种操作：1.get(key) 检查key是否在缓存中，在则取出，并重新放到链表的头节点。
put(key,value):如果key存在，则更新其值。不再 则插入，但是需要检查容量是否满了，满了则需要删除链尾节点
"""

#定义双链表节点
class Node:
    def __init__(self,key,value):
        self.key = key
        self.value = value
        self.Prev = None
        self.Next = None

class LRUCache:

    def __init__(self, capacity: int):
        self.capacity = capacity
        self.cache ={} #哈希表存储key和对应的节点，实现O(1)的查找
        #定义双链表
        self.head = Node(0,0)
        self.tail = Node(0,0)
        self.head.Next = self.tail
        self.tail.Prev = self.head

    def remove(self,node):
        pre_node = node.Prev
        next_node = node.Next
        pre_node.Next = next_node
        next_node.Prev = pre_node

    def insert(self,node):
        head_next = self.head.Next
        self.head.Next = node
        node.Prev = self.head
        node.Next = head_next
        head_next.Prev = node


    #将某个已经存在的节点移动到链头--> 先删除该节点，再重新插入到链头
    def get(self, key: int) -> int:
        "检查key是否在cache中"
        if key in self.cache:
            node = self.cache[key]
            self.remove(node)
            self.insert(node)
            return node.value
        else:
            return -1
        

    def put(self, key: int, value: int) -> None:
        "key存在，则更新，不存在，检查容量，并插入；都要把节点重新放入到链头"
        if key in self.cache:
            node = self.cache[key]
            node.value = value
            #重新放入到链头
            self.remove(node)
            self.insert(node)
        else:
            #检查容量
            if len(self.cache) == self.capacity:
                #删除练尾节点
                tail_node = self.tail.Prev
                self.remove(tail_node)
                del self.cache[tail_node.key]

            #重新插入
            node = Node(key,value)
            self.insert(node)
            self.cache[key] = node

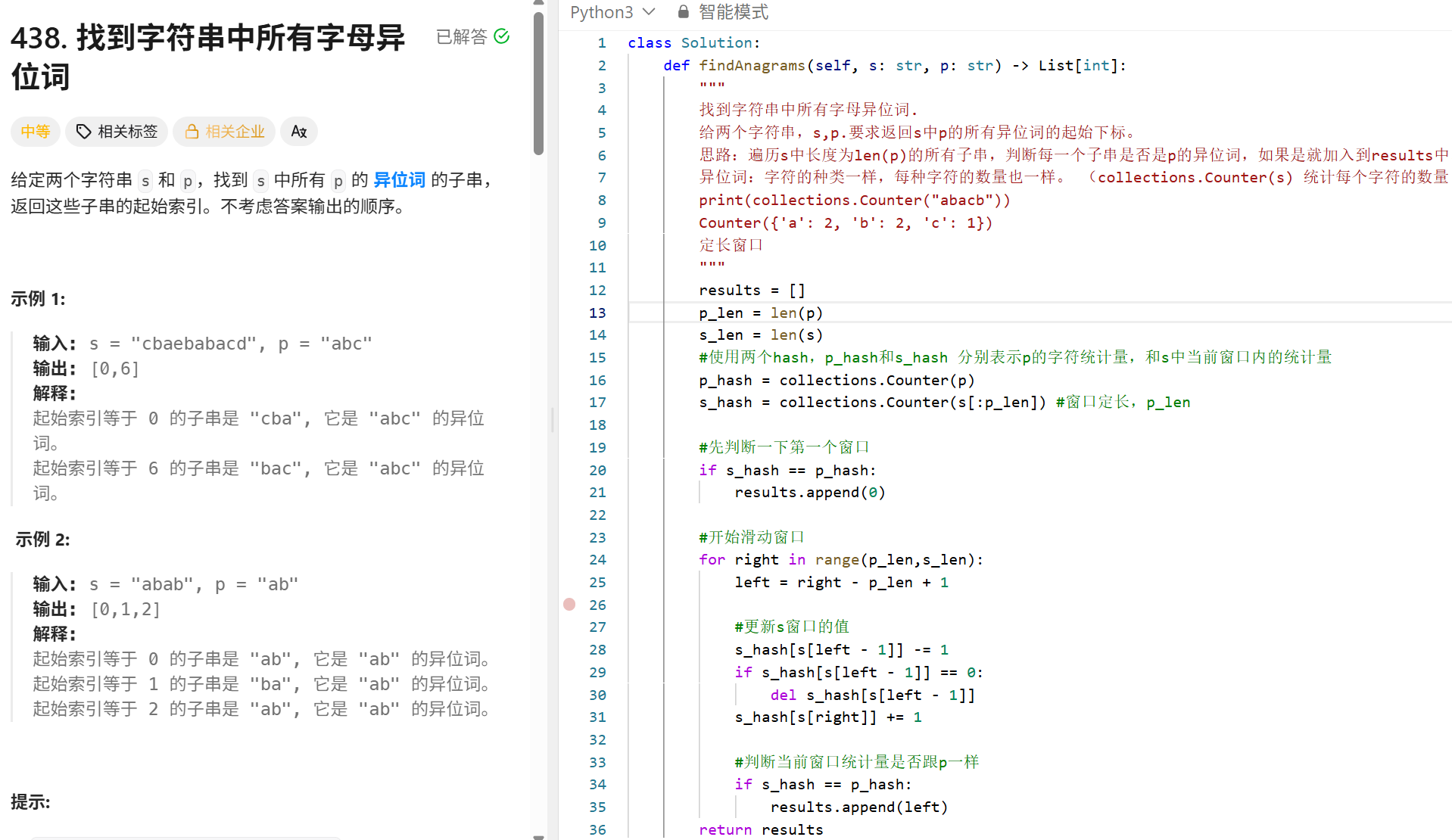
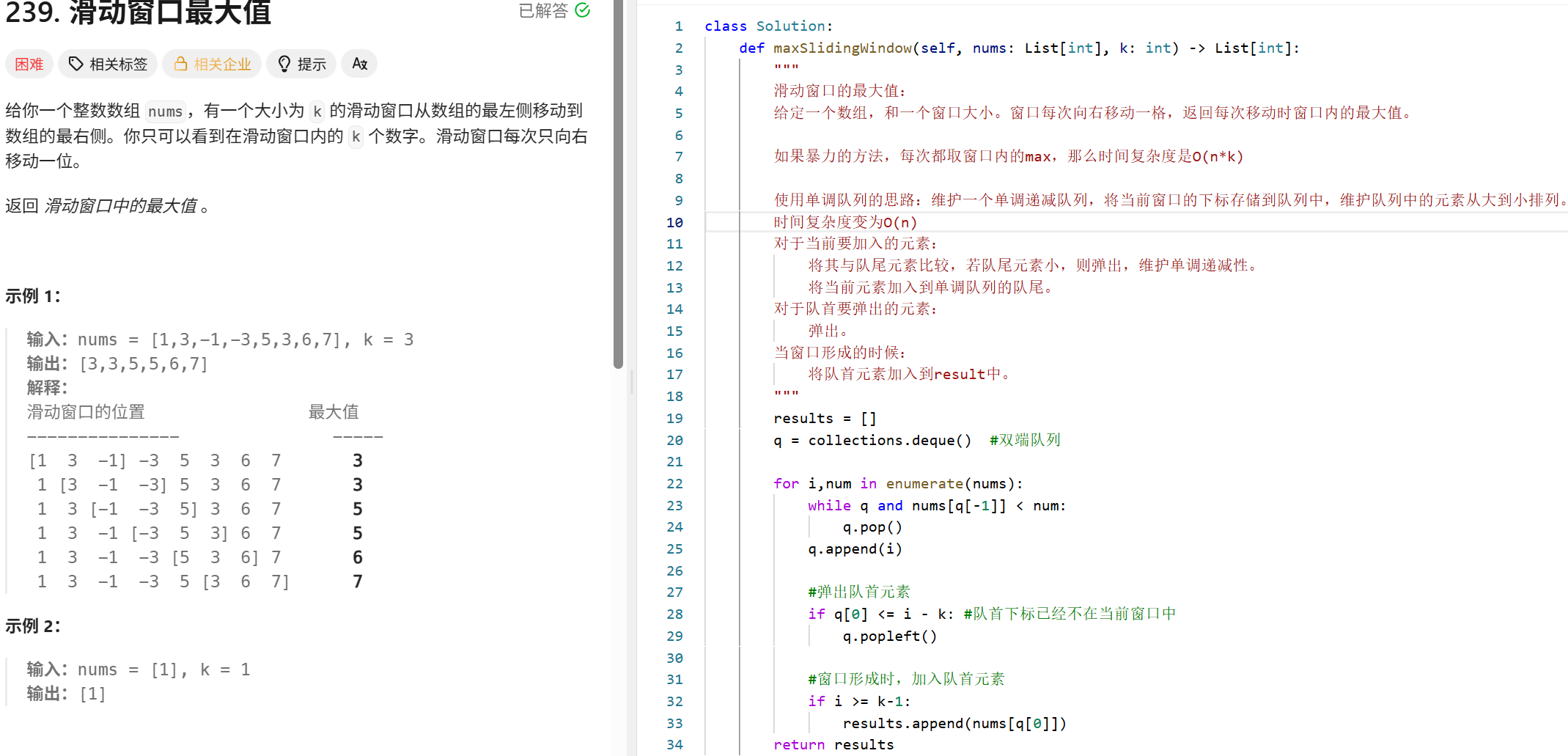
滑动窗口

class Solution:
    def minWindow(self, s: str, t: str) -> str:
        """
        最小覆盖子串：给定两个字符串s,t；要求返回s中包含t所有字符的最短子串.
        覆盖：字符种类，数量要跟t相同。使用match_count 表示当前子串中有多少字符满足数量需求。
        使用一个哈希表表示滑动窗口。用left，right表示当前窗口的边界。
        扩展窗口，添加字符：遍历s，将当前字符加入到窗口中。
            判断窗口中新加入的字符的数量是否满足需求，如果满足，那么match_count += 1
        缩小窗口：若窗口中所有字符都满足t中字符的需求：
            尝试left左移动，若移除的字符不再满足数量需要，还需要更新match_count；同时还需要更新一下start和min_len；
        最后 子串: s[start:start + min_len]
        """
        #窗口
        windows = collections.defaultdict(int)
        t_hash = collections.Counter(t)
        left = 0
        match_count = 0

        start, min_len =0, float("inf")

        #遍历s，扩展窗口
        for right, val in enumerate(s):
            windows[val] += 1

            #判断新加入的字符是否满足数量需求
            if val in t_hash and windows[val] == t_hash[val]:
                match_count += 1
            
            #当窗口内所有字符都满足要求时，尝试缩短
            while match_count == len(t_hash):
                #更新start 和min_len
                if right - left + 1 < min_len:
                    min_len = right - left + 1
                    start = left

                windows[s[left]] -=1
                #检查数量是否减到不满足条件
                if s[left] in t_hash and windows[s[left]] < t_hash[s[left]]:
                    match_count -= 1
            
                left += 1
        return s[start:start + min_len] if min_len != float("inf") else ""

单调栈

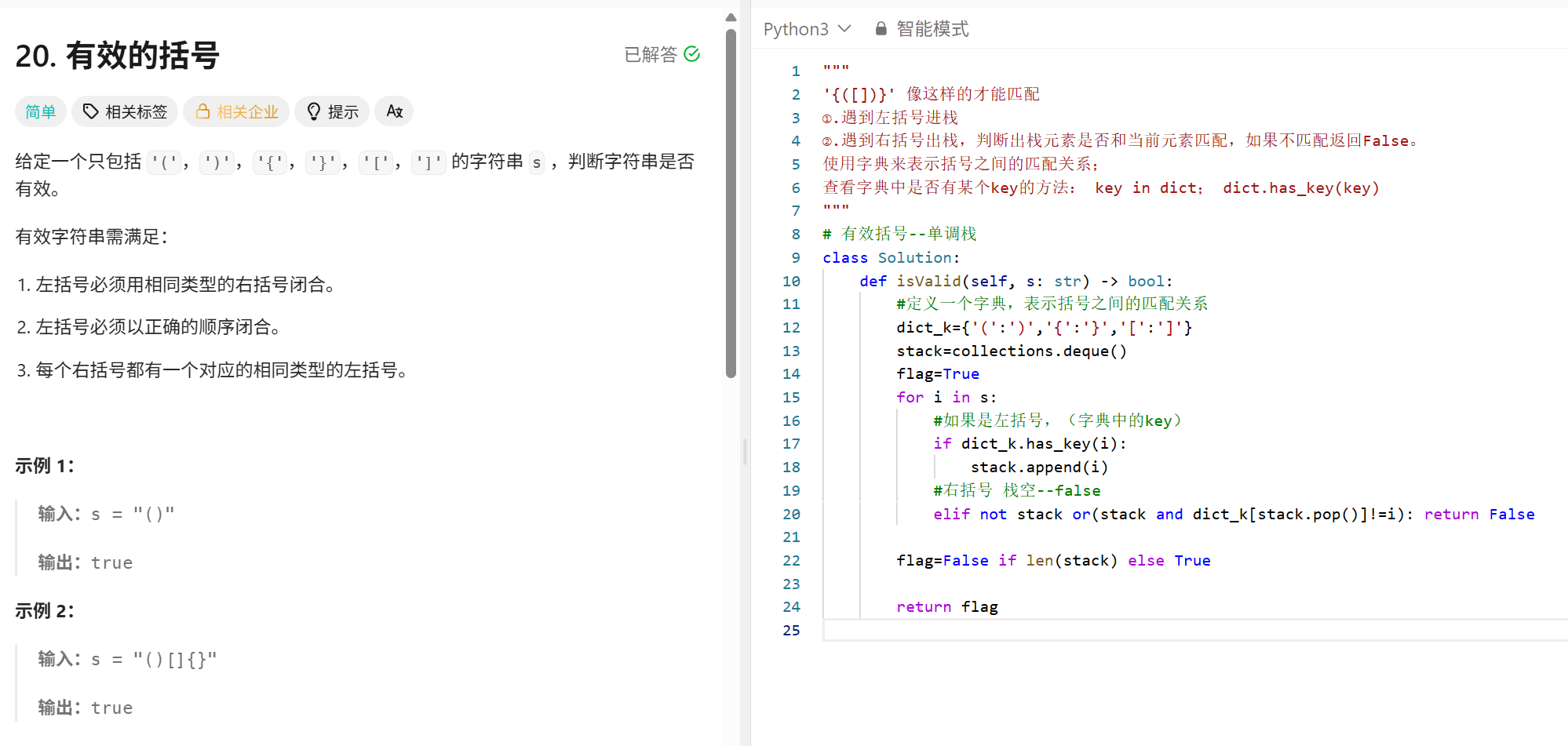
简化路径：

"""
给定一个Unix风格的路径字符串；
要求把她变成一个规范路径；

规范路径的定义：
始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/' 。
最后一个目录名（如果存在）不能 以 '/' 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

输入：path = "/.../a/../b/c/../d/./"

输出："/.../b/d"
"""
"""
方法就是使用栈来操作，实现元素的添加和删除。

①.遇到 "." 或者 "" 就什么也不做 (空串就相当于是遇到了连续的//。
②.遇到 ".." 弹出栈顶元素。
③.else 加入栈
"""
import collections
class Solution:
    def simplifypath(self, path: str) -> str:
        stack = collections.deque()

        path_list = path.split("/")
        for s in path_list:
            if s == "..":
                if stack: #注意判空！！  “/../”
                    stack.pop()
            elif s != "." and s:
                stack.append(s)
        return "/" + "/".join(stack)

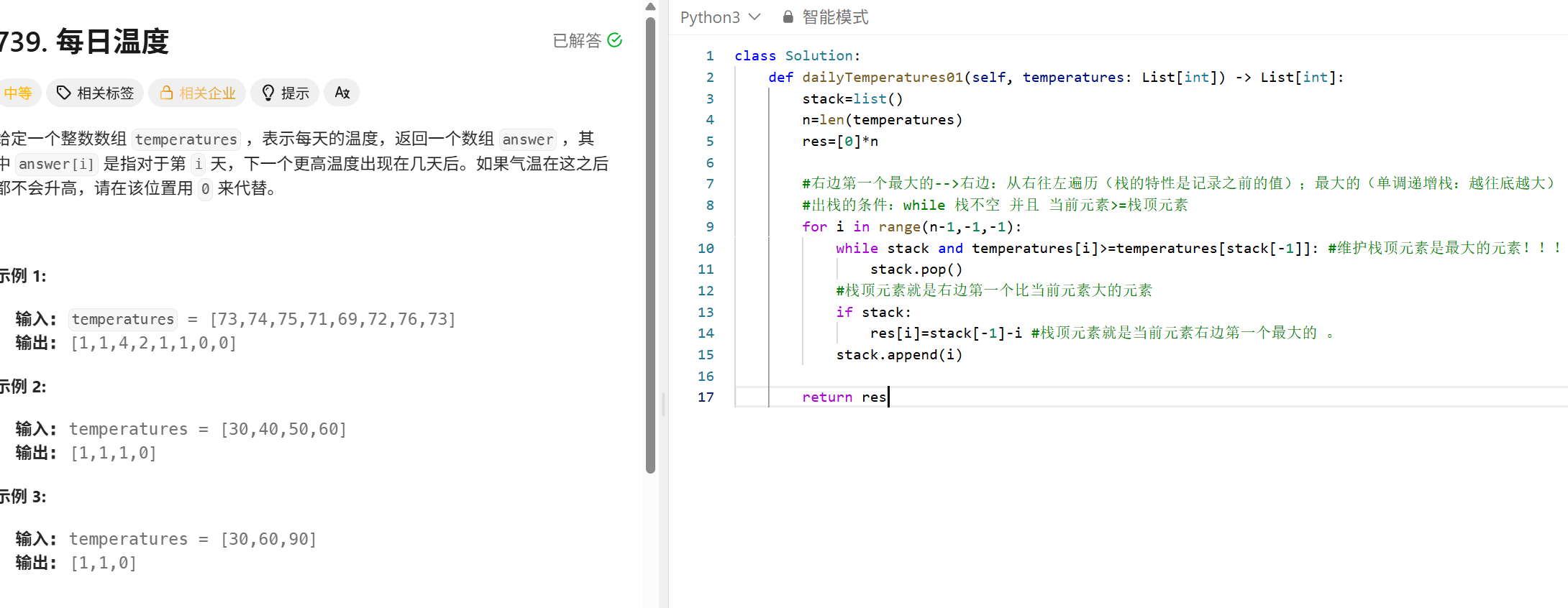
股票价格跨度

"""
题目需求：
设置一个类，实现对于给定当前的股票，找到该股票之前有多少天都是连续小于等于他的。
把这个值叫做 跨度(span),并返回。

例如
[[], [100], [80], [60], [70], [60], [75], [85]]
输出：
[null, 1, 1, 1, 2, 1, 4, 6]
"""
import collections

"""
方法：
暴力方法： 对于当前股票的跨度，往前挨个比较，找到每一天的跨度。这样复杂度是O(n^2)

栈里面存储着每一天股票的价格和跨度（price，span）; 维护一个单调递减栈(栈顶的股票价格是小的)； 

当前股票>=栈顶，那么就弹出栈顶。并将栈顶的跨度累加到当天股票跨度上。
初始时，所有股票的跨度都是1.
"""
class StockSpanner:
    def __init__(self):
        self.stack=collections.deque()

    def next(self, price: int) -> int:
        span = 1
        while self.stack and price >= self.stack[-1][0]:
            span += self.stack.pop()[1]

        self.stack.append((price,span))

        return span

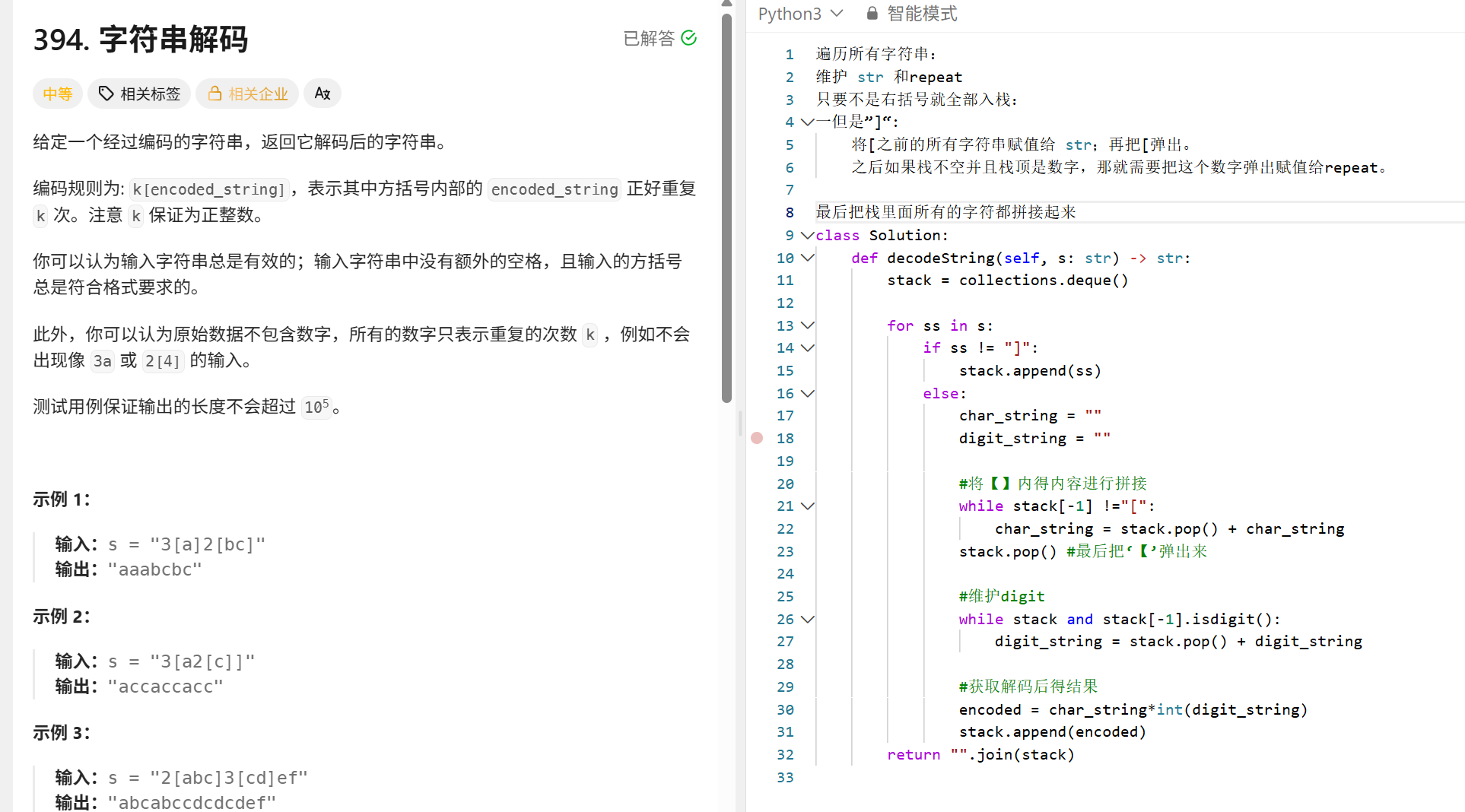
后缀表达式求值

"""
逆波兰表达式(后缀表达式)：
数字在前，算符在后。
适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中。

题目：给定一个后缀表达式字符数组。
求出这个表达式的值。
"""
import collections
from operator import add, sub, mul
from typing import List

"""
注意：
向零取整：
int( / ) 浮点运算+向零取整 ；如int(-5 / 2) = -2

向下取整 //：
-5 // 2 = -3 
"""
def evalRPN(tokens: List[str]) -> int:
    stack = collections.deque()
    # 注意 除法是向截断
    operate_exp = {
        "+": add,
        "-": sub,
        "*": mul,
        "/": lambda x, y: int(x / y)
    }

    for token in tokens:
        try:
            num = int(token)
        except ValueError:
            "这里需要注意顺序；如 1 2 + ; num2是2；num1是1"
            num2 = stack.pop()
            num1 = stack.pop()
            num = operate_exp[token](num1, num2)  # 查字典获取对应的算符函数
        finally:
            stack.append(num)

    return stack[-1]

基本计算器

"""
基本计算器：
给你一个字符串表达式 s ，请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数，比如 eval() 。

示例 3：
输入：s = "(1+(4+5+2)-3)+(6+8)"
输出：23

"""
import collections


def calculate(s: str) -> int:
    """
    ”123+1“
    设计三个变量：
    res:当前累计的结果
    num:当前拼接的结果
    sign:num的符号
    """
    stack = collections.deque() #占用来存储 "("之前的累计结果和符号
    res = 0
    num = 0
    sign = 1

    for c in s:
        if c.isdigit():
            num = num * 10 + int(c)
        elif c == "+":
            res += sign * num
            num = 0
            sign = 1
        elif c == "-":
            res +=sign * num
            num = 0
            sign = -1
        # "(1+(4+5+2)-3)+(6+8)" 遇到"("需要存储前面的res和sign；同时重置res和sign
        elif c == "(":
            #注意顺序
            stack.append(res)
            stack.append(sign)
            res = 0
            sign = 1
        # 如果遇到")" 那么就需要将当前括号的内容进行累加；同时需要弹出栈顶元素，将当前括号和当前括号前面的内容进行累加
        elif c == ")":
            res += sign * num
            res *= stack.pop()
            res += stack.pop()
            num = 0

    # 如果表达试最后一个字符是数字，那么还需要累计到结果当中
    res += sign * num
    return res

双指针：

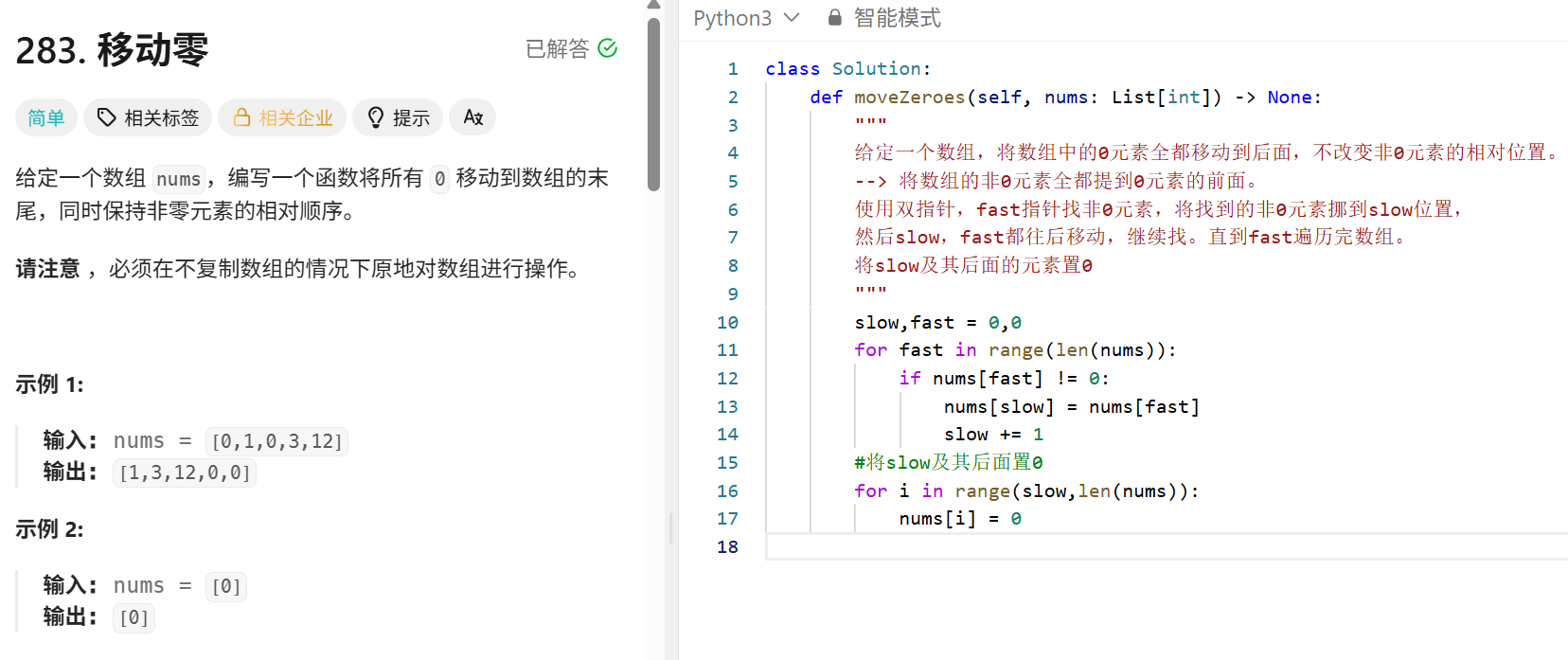
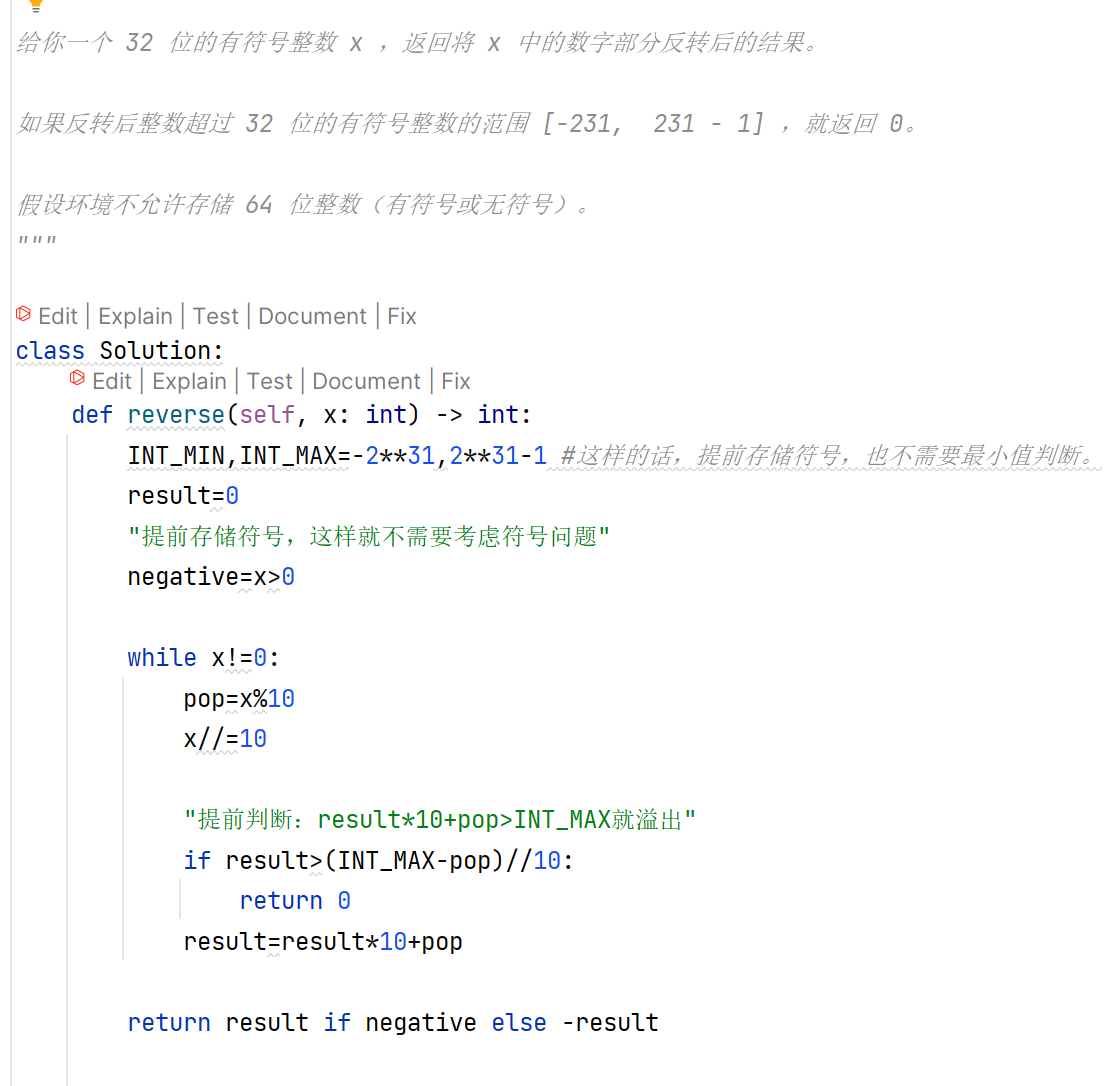
反转32位有符号整数：

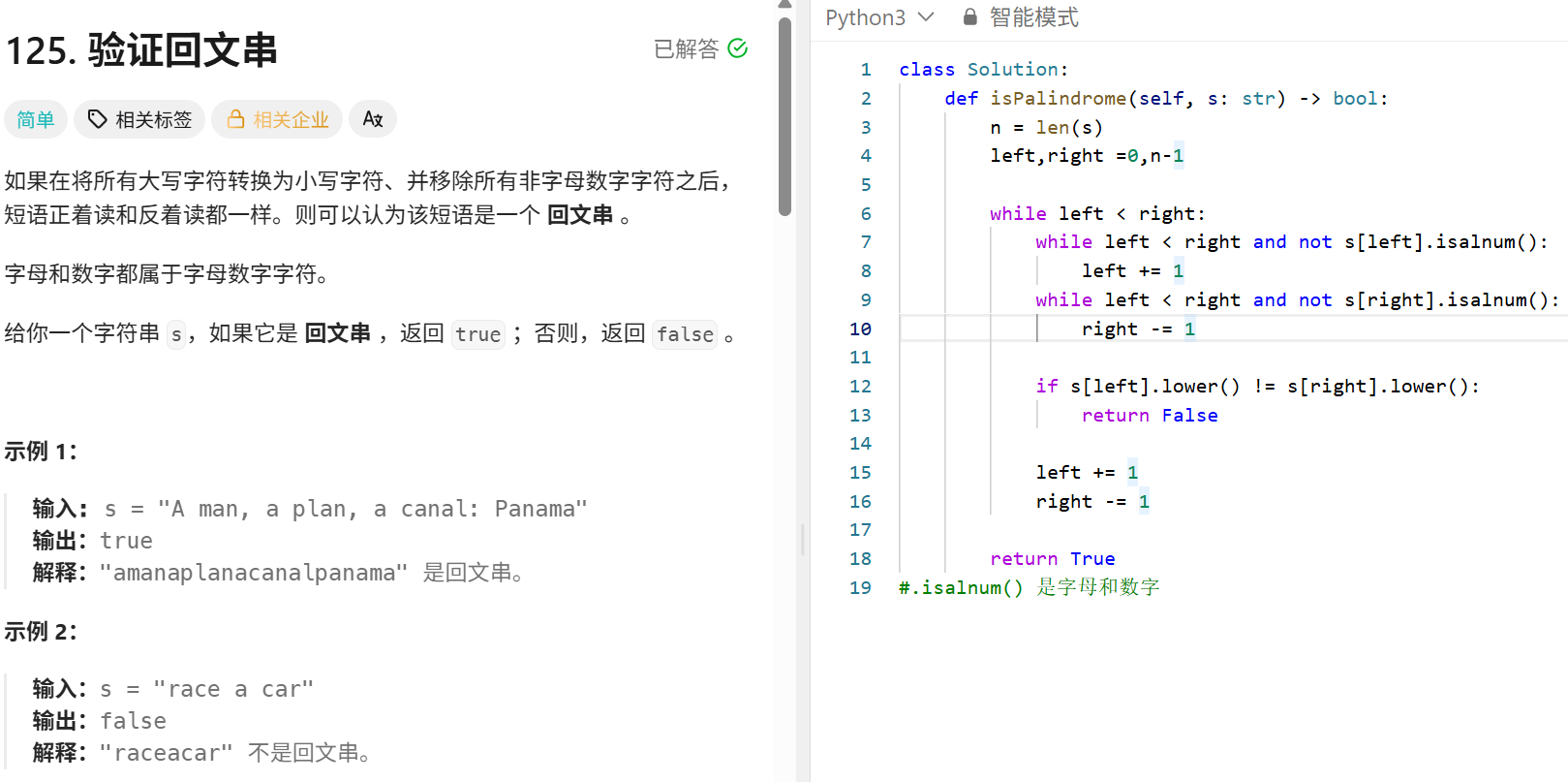
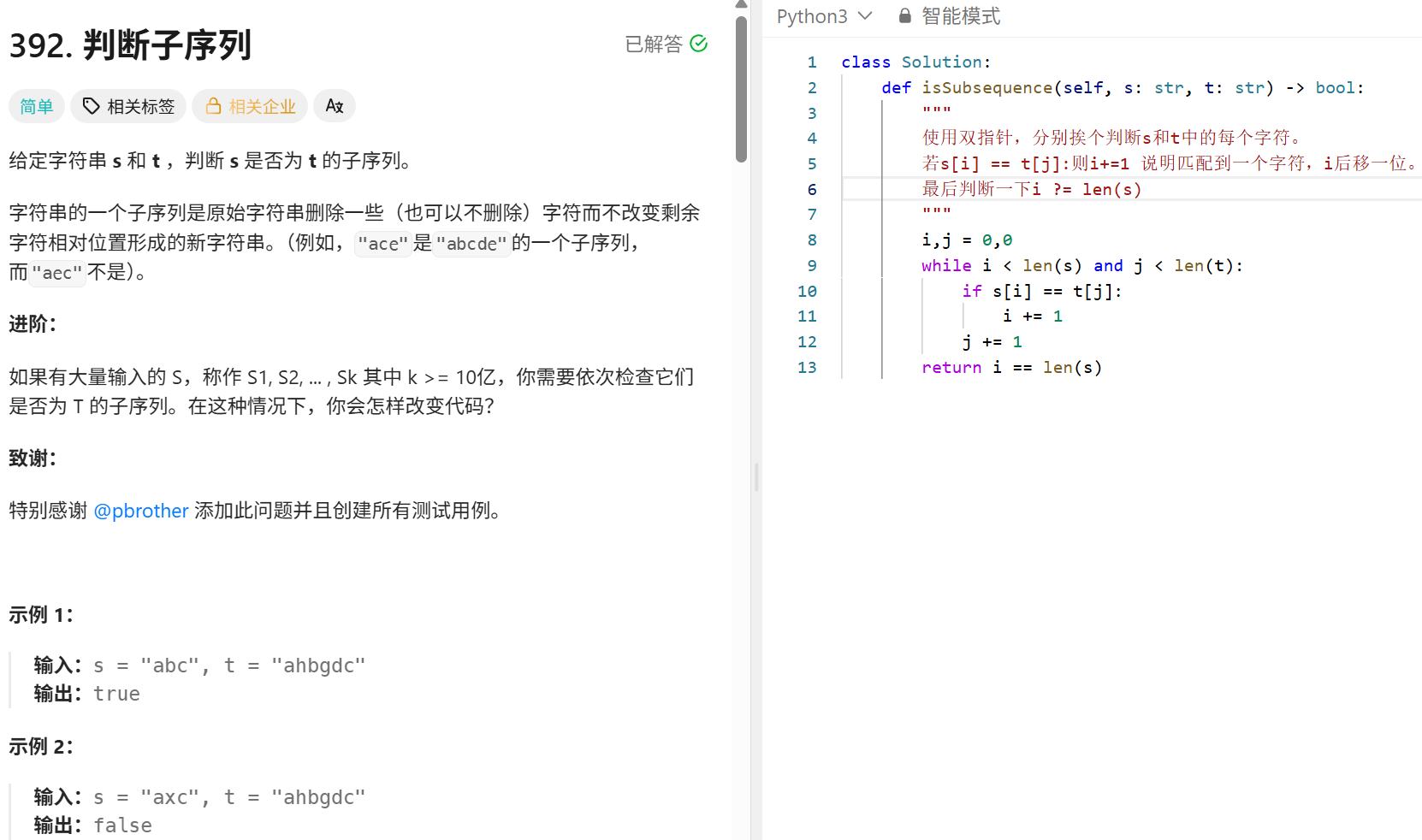
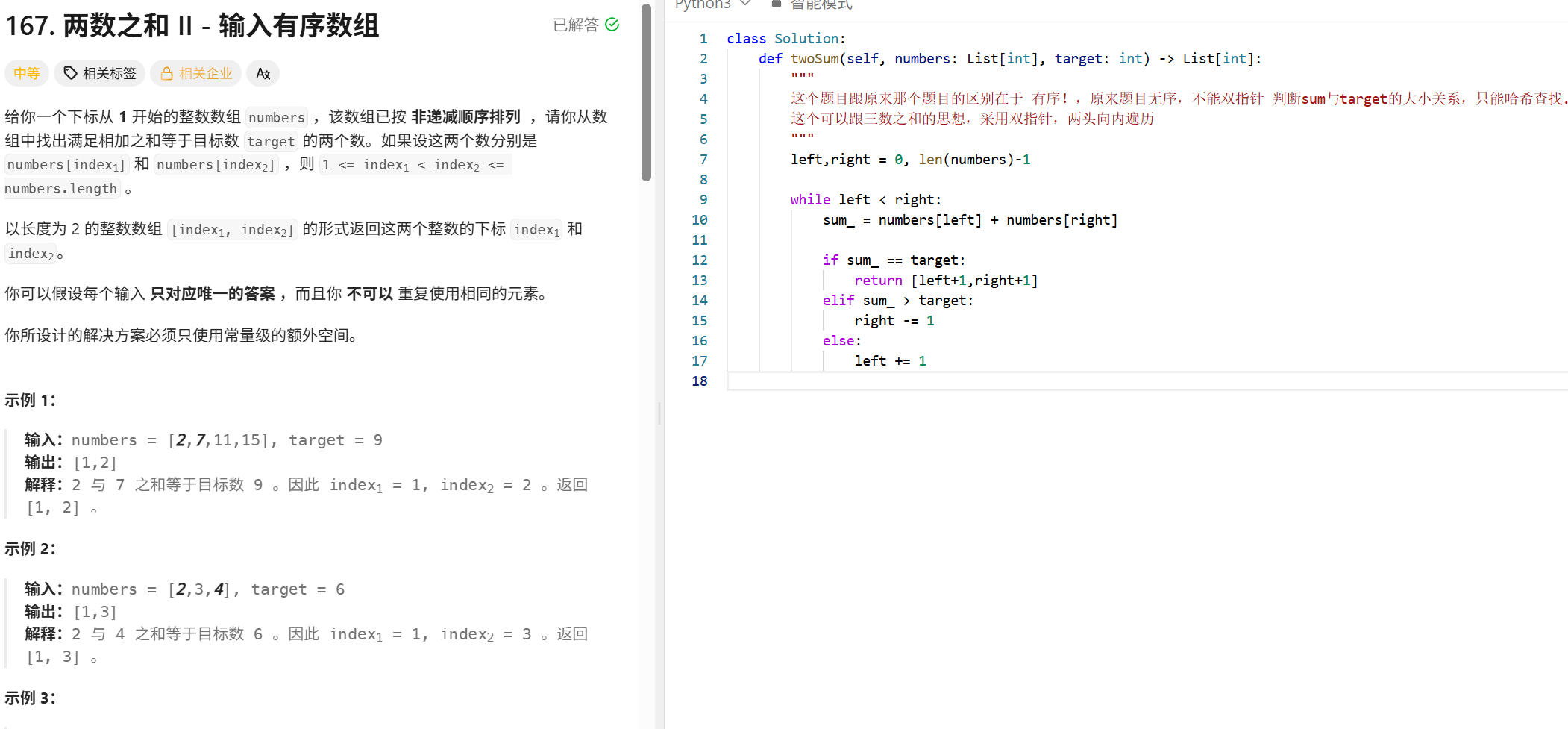
X数字之和

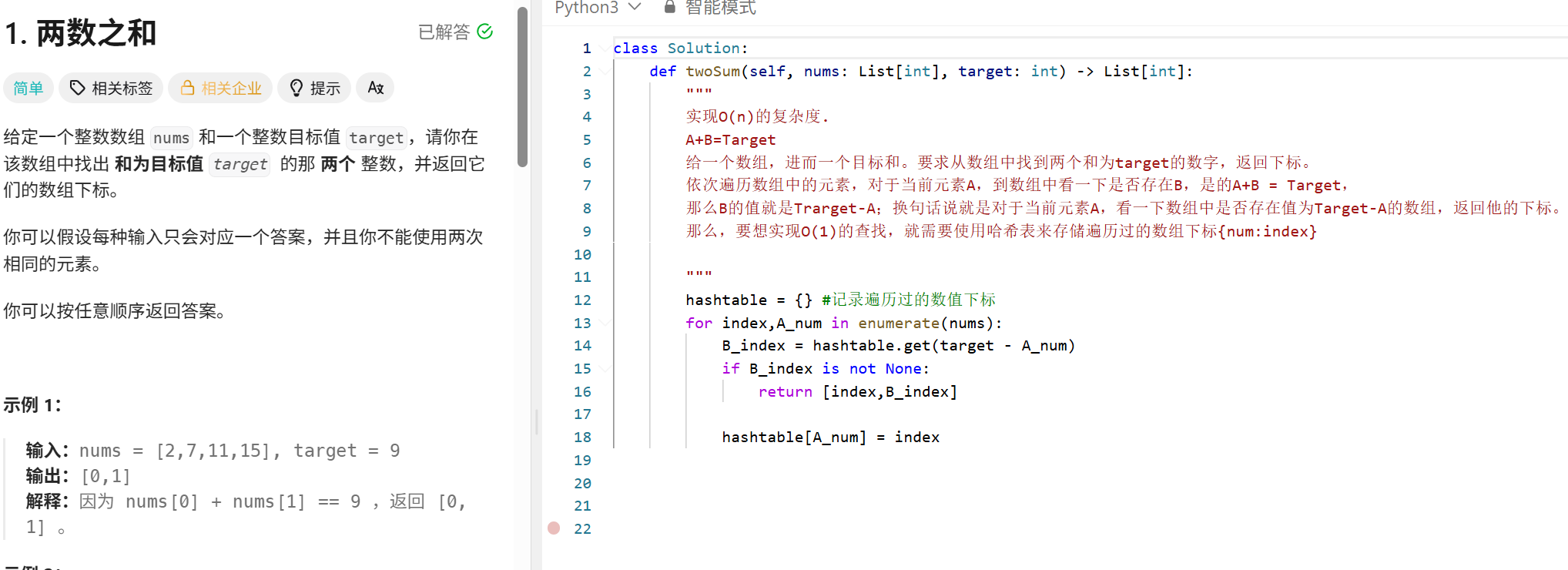
class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        """
        A+B+C =  0
        A L R

        给你一个数组，从中找出和为0的三个元素的所有集合。

        A+nums[L]+nums[R]=0
        固定一个元素A，使用双指针L,R找另外两个满足和为0的元素。

        注意这里需要处理重复元素：
        nums[L] == nums[L+1] 则需要 L++
        nums[R] ==nums[R-1] 则需要 R--

        nums[i] == nums[i-1] i也是需要跳过的。

                从数组中找个三个不相同的数字，要求其和为0；
        找出满足这个条件的全部不重复的三元组。
        先排序;
        使用一个固定指针i
        Left=i+1,right=n-1
        i+left=right=0
        根据sum与0的大小关系来决定移动left还是right
        """
        if len(nums) < 3:
            return []
        
        results = []

        #先排序
        nums.sort()
        for i in range(len(nums)):
            if nums[i] >0:
                return results
            
            #判断有没有必要计算以 i 开头的三元组
            if i >0 and nums[i] == nums[i-1]:
                continue

            #L ,R
            left,right = i+1, len(nums) - 1
            while left < right:
                sum_num = nums[i] + nums[left] + nums[right]
                if sum_num == 0:
                    results.append([nums[i], nums[left], nums[right]])
                    #去重left,right
                    while left < right and nums[left] == nums[left+1]: left += 1
                    while left < right and nums[right] == nums[right - 1]: right -= 1

                    left += 1
                    right -= 1

                elif sum_num > 0:
                    right -= 1
                else:
                    left += 1
        return results

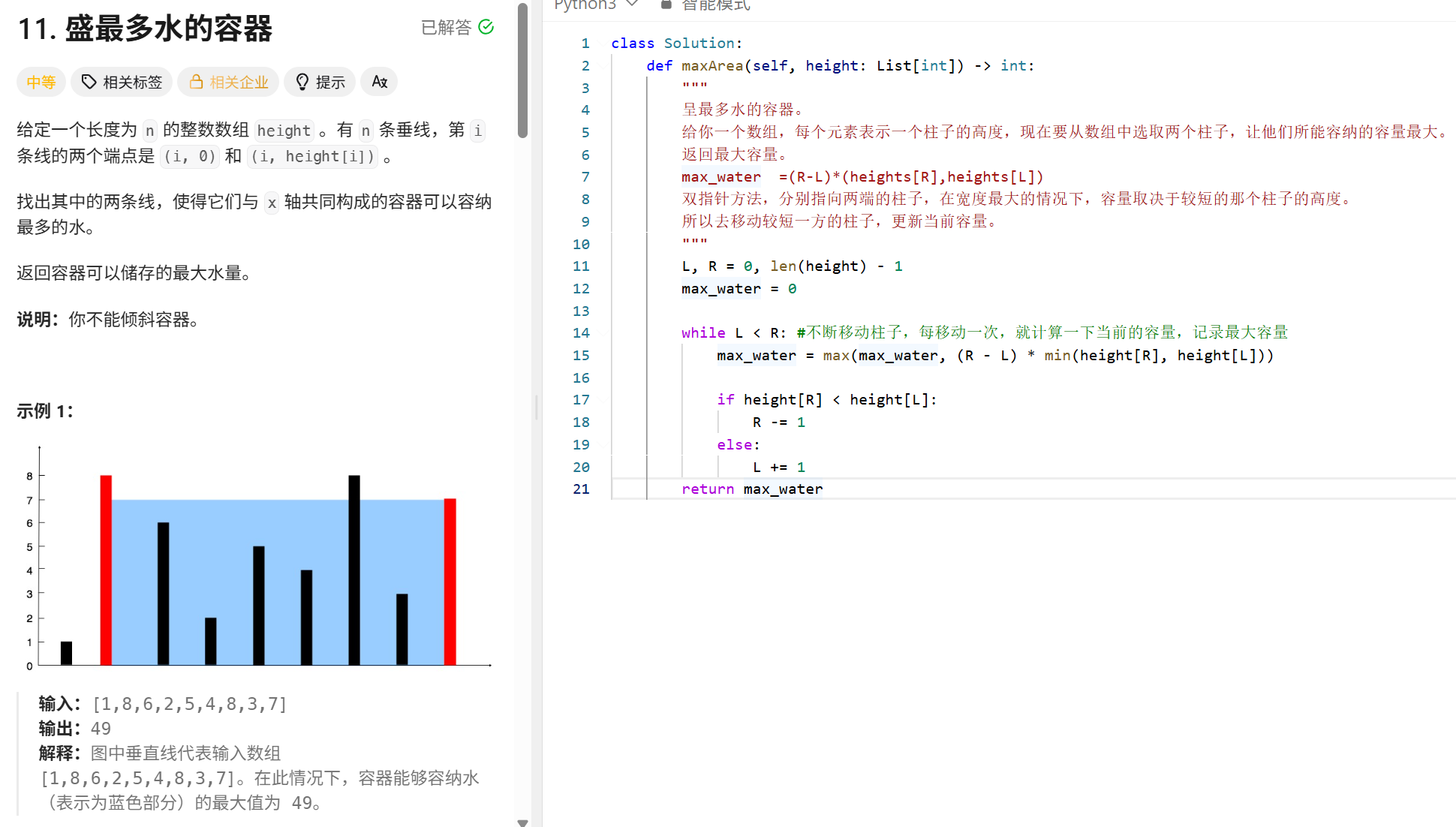
接雨水：

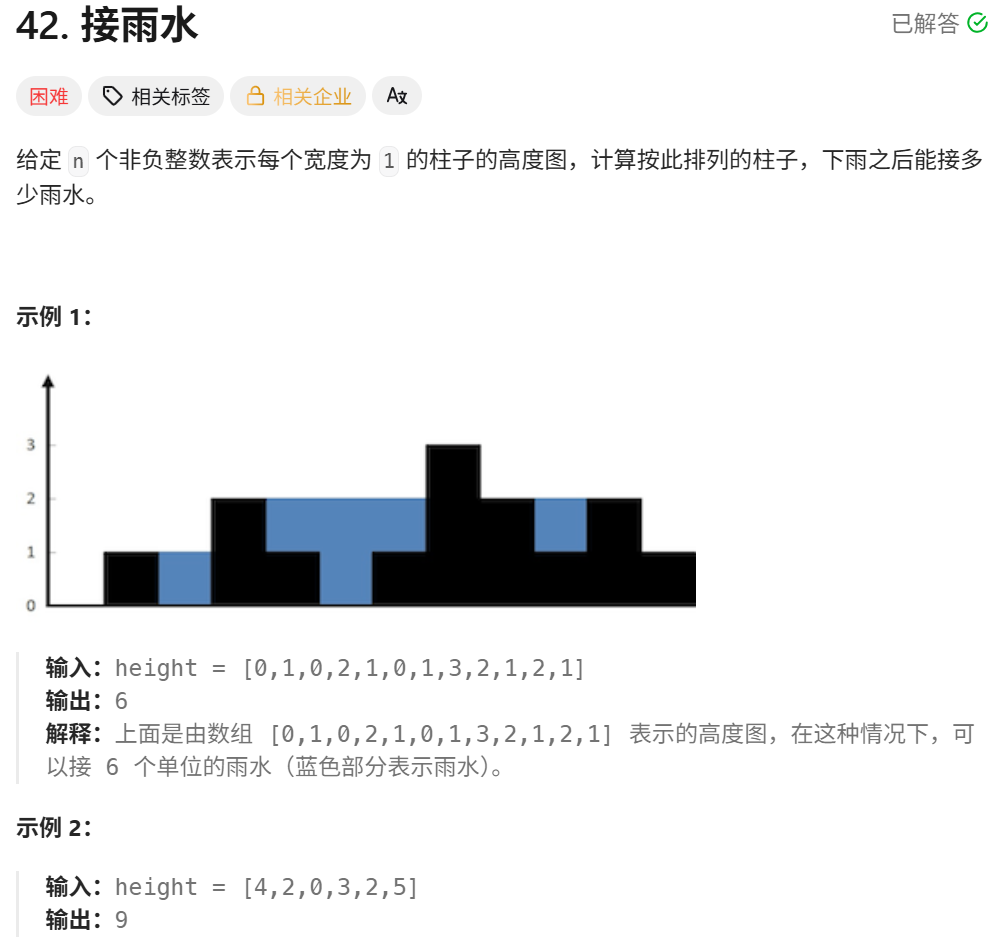
动态规划:

时间复杂度：O(n) （三次遍历）

空间复杂度：O(n) （两个辅助数组）

class Solution:
    def trap(self, height: List[int]) -> int:
        """
        动态规划：
        每个柱子的存水量 = cur_water = min(max_left[i], max_right[i]) - height[i]
        即： 当前柱子左边最高柱子和右边最高柱子中两者较短的那个 减去当前柱子的高度。
        那么累积所有柱子的存水量即可。
        现在需要计算max_left[i] 数组和max_right[i]数组。
        定义max_left[i] 表示从0..i范围内最高柱子的高度 = max(max_left[i-1], height[i])
        max_right[i] 表示 i..n-1范围内最高柱子的高度 = max(max_right[i+1], height[i])
        """
        if not height or len(height)<2:
            return 0

        n = len(height)
        max_left,max_right= [0]*n, [0]*n
        
        max_left[0] =  height[0]
        for i in range(1,n):
            max_left[i] = max(max_left[i-1],height[i])
        
        max_right[n-1] = height[n-1]
        for i in range(n-2,-1,-1):
            max_right[i] = max(max_right[i+1],height[i])

        #累积所有柱子
        result = 0
        for i in range(n):
            result += min(max_left[i], max_right[i]) - height[i]
        
        return result

双指针

class Solution:
    def trap(self, height: List[int]) -> int:
        """
        双指针：
        动态规划方法中需要两个数组max_left[i]和max_right[i]来存储左右柱子的最大高度。
        使用双指针方法，实时记录当前柱子的最大高度。
        左右指针所指的柱子进行比较，谁短优先计算谁，
        假设height[left] < height[right],优先计算左右柱子。
        那么每条柱子的存水量就是 cur_water = max_left - height[left] 
        """
        n = len(height)
        #定义双指针
        left, right = 0, n-1
        #定义柱子最大高度
        max_left,max_right = height[left], height[right]

        result = 0

        while left < right:
            #水位取决于较短的柱子
            if height[left] <height[right]:
                left += 1
                #更新最大高度
                max_left = max(max_left, height[left])
                cur_water = max_left - height[left]
                result += cur_water
            else:
                right -= 1
                max_right = max(height[right], max_right)
                cur_water = max_right - height[right]
                result += cur_water
        return result
                

单调栈

class Solution:
    def trap(self, height: List[int]) -> int:
        """
        单调栈：
        只有形成凹槽的时候才能够接水。
        那么使用一个单调递减栈，只有当前元素>栈顶的时候才能形成凹槽
        if height[i] > stack[-1]:
            弹出栈顶，此时左右两边的高柱子就是stack[-1],height[i]
            那么此时柱子 存水量为：min(stack[-1],height[i]) - 弹出的栈顶柱子的高度.
        """
        n = len(height)
        results = 0
        #定义单调递减栈,存储的是下标
        stack = []

        #遍历柱子，维护递减
        for i, h in enumerate(height):
            #只有当前高度>栈顶的时候 才能形成凹槽
            while stack and h >height[stack[-1]]:
                #弹出栈顶(曹底)
                bottom_index = stack.pop()
                #判断一下左边还有没有柱子
                if not stack:
                    break

                max_left_index = stack[-1]
                
                results += (min(height[max_left_index], height[i]) - height[bottom_index]) * (i-max_left_index-1)
            stack.append(i)
        return results

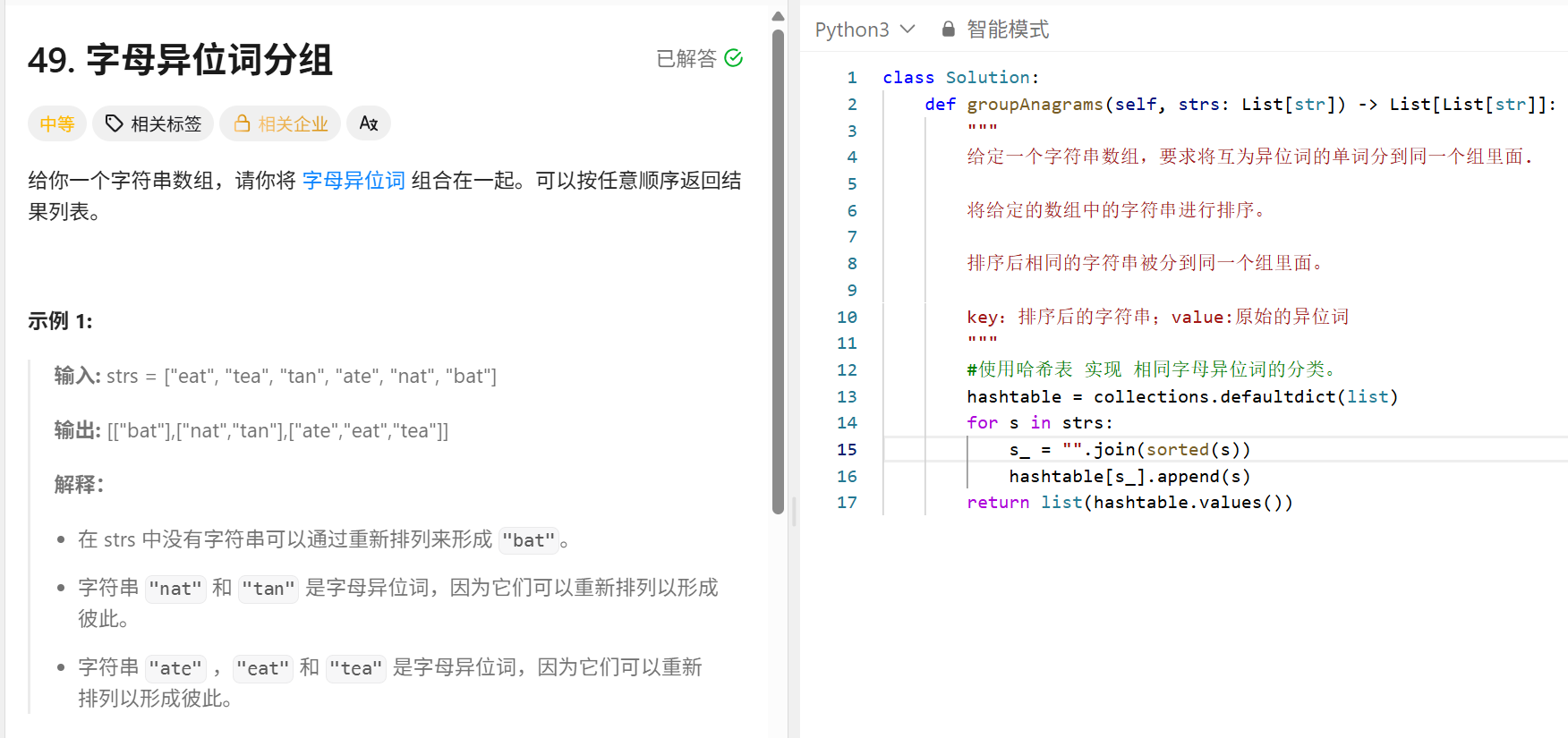
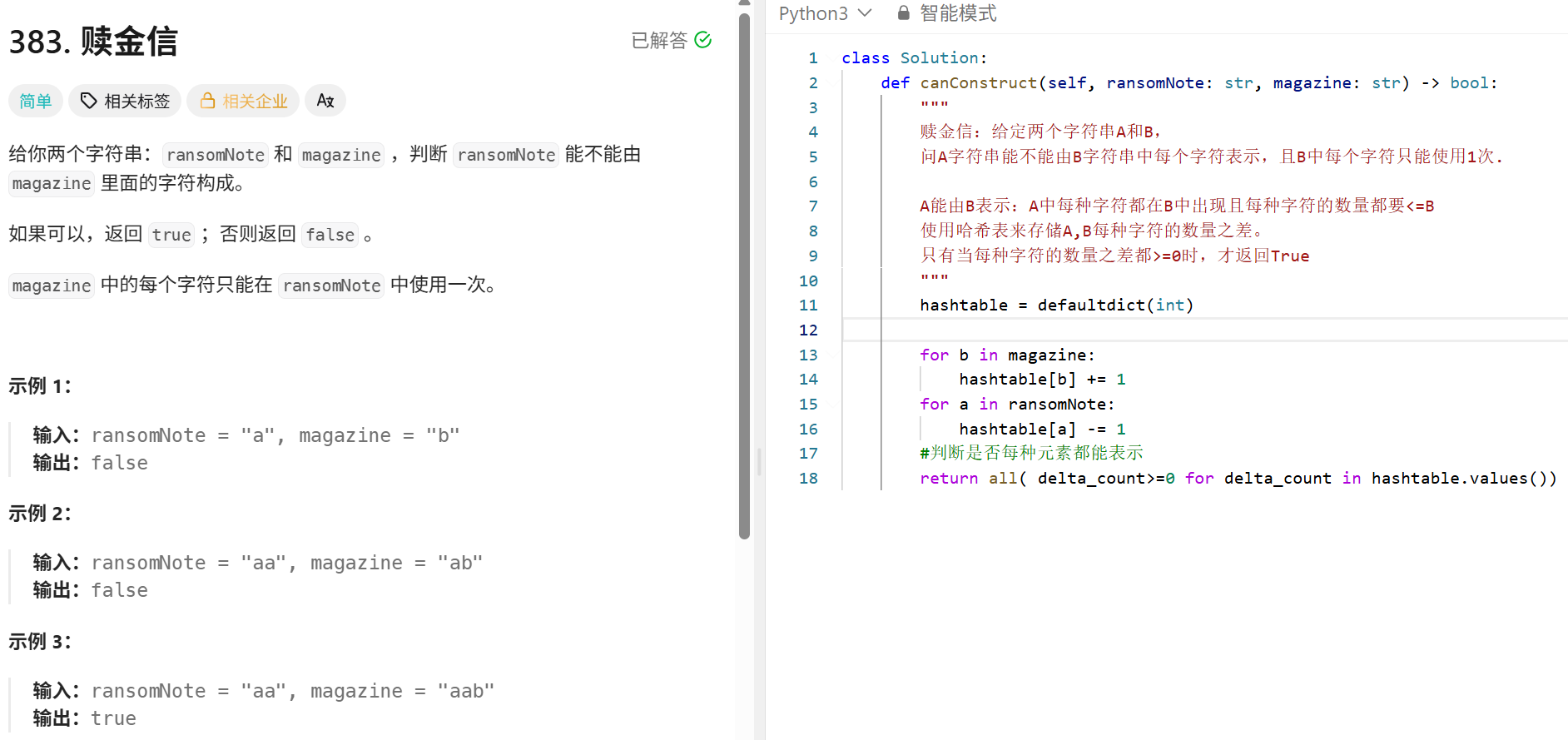
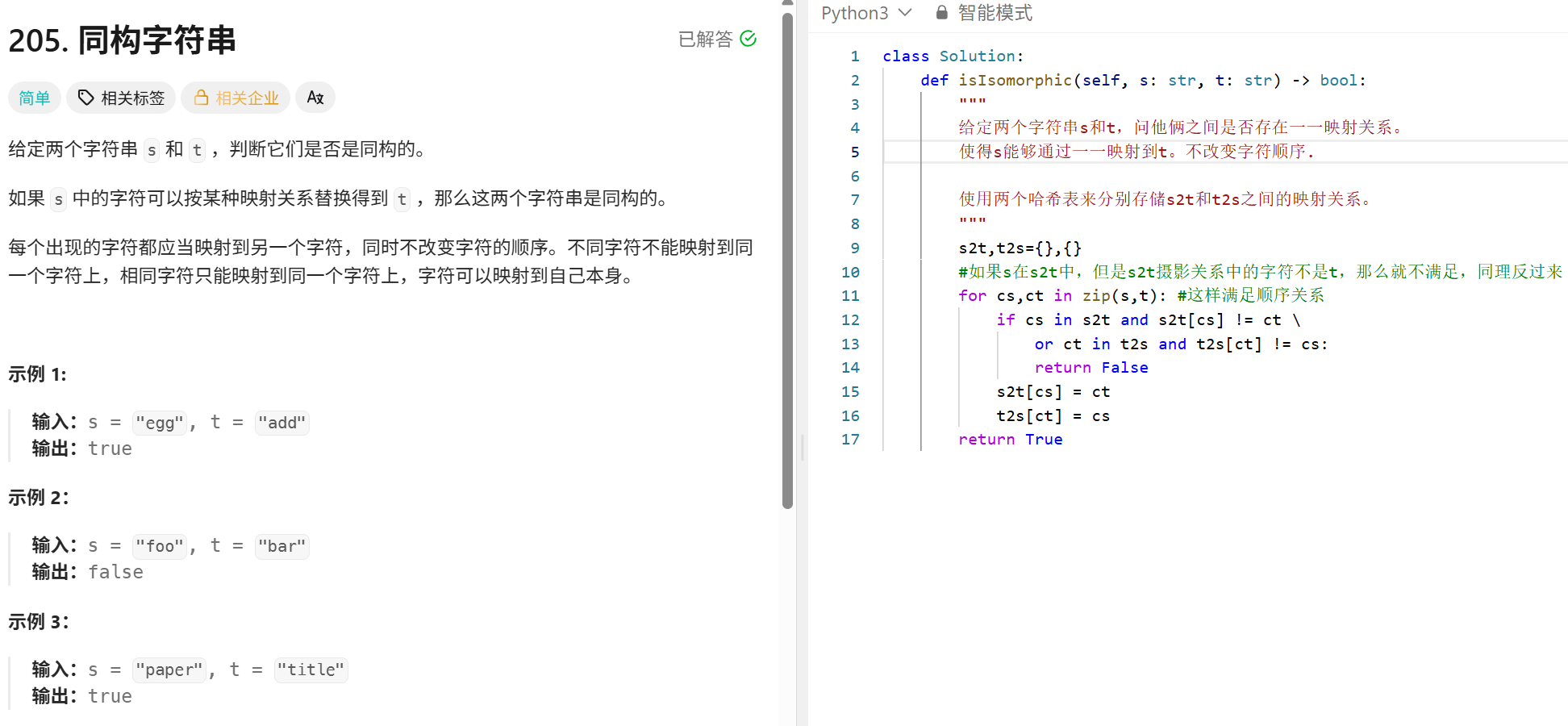
哈希表：

贪心算法

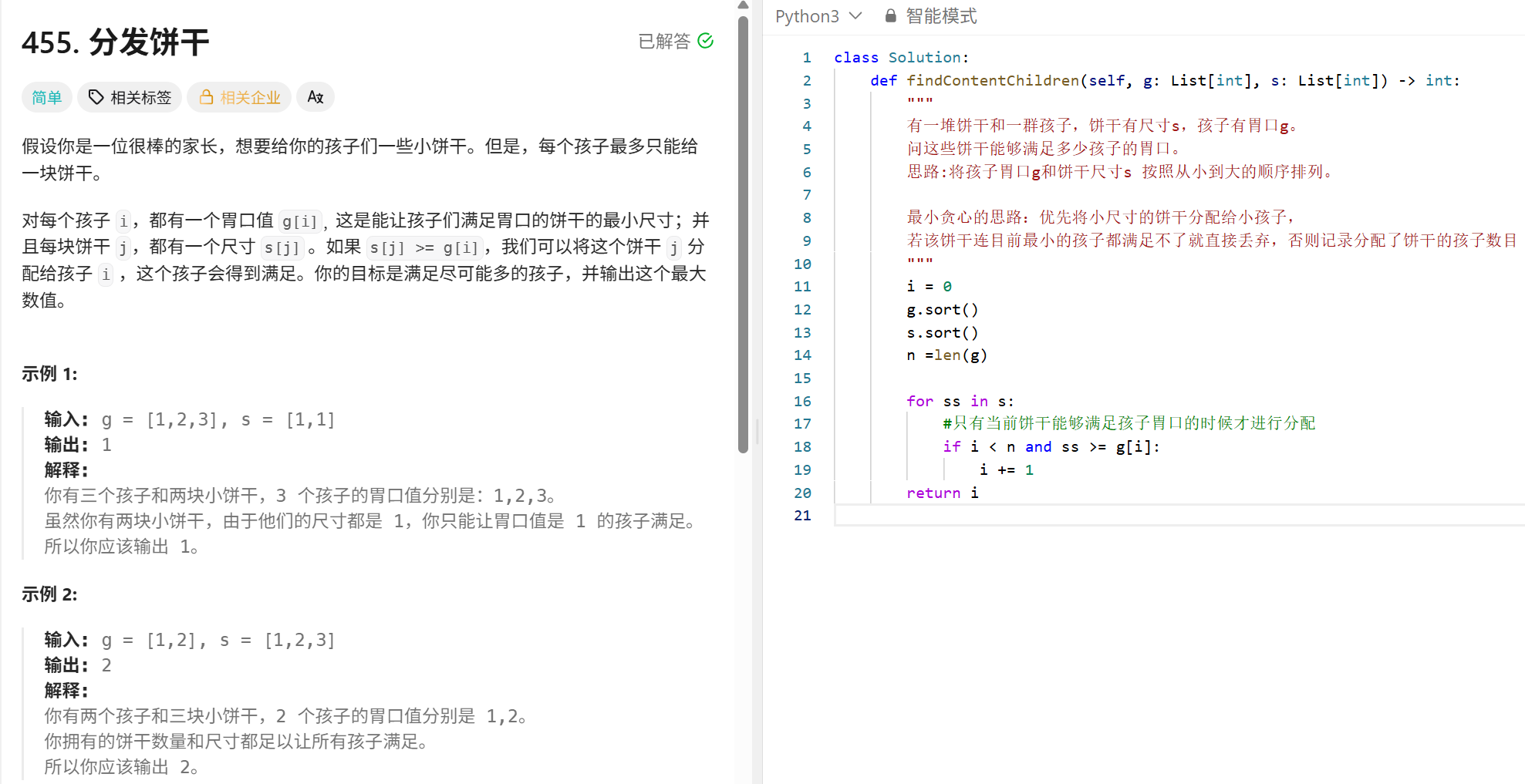
class UnionFind:
    def __init__(self,n):
        self.list = list(range(n))
    #查找操作
    def Find(self,x):
        if self.list[x] == x:
            return x
        self.list[x] = self.Find(self.list[x])
        return self.list[x]

    #合并操作
    def union(self,a,b):
        rootA = self.Find(a)
        rootB = self.Find(b)
        if rootA != rootB:
            self.list[rootA] = rootB
    

class Solution: 
    def maxEvents(self, events: List[List[int]]) -> int:
        """
        要想参加尽可能多的会议，需要保证早开始早结束，
        优先参加结束时间早的会议，确保参加的会议数量多，
        在结束时间相同的情况下，优先参加开始时间早的会议，保证后面预留足够多的时间
        思路:
        1.按照结束时间排序，结束时间相同，按照开始时间排序。
        2.遍历排序后的数组，在start-end之间找到第一个空闲时间。这里使用并查集实现O(1)的查找空闲时间
        """
        #排序
        events.sort(key = lambda x:(x[1],x[0]))
        #定义并查集
        max_days = events[-1][1]
        uf = UnionFind(max_days + 2) #确保并查集的大小涵盖所有可能的天数 0~max_day

        #遍历排序数组，找到一个空闲天数
        res = 0
        for event in events:
            a, b = event
            #找当前会议区间内第一个空闲天数
            free_day = uf.Find(a)
            #如果当前空闲天数在该会议区间内，则选择参加，并堆并查集进行更新
            if free_day <= b:
                res += 1
                uf.union(free_day, free_day+1)
        return res

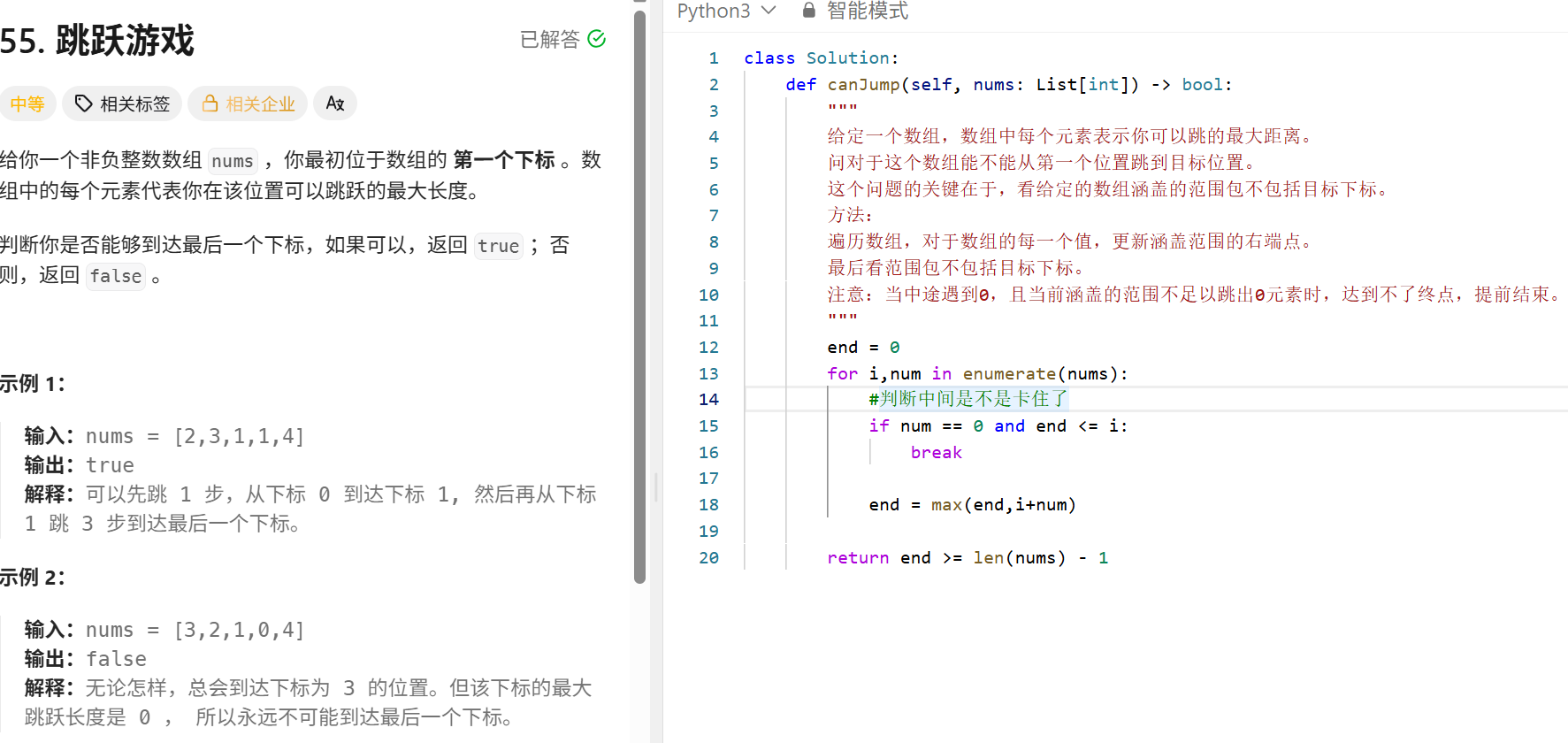
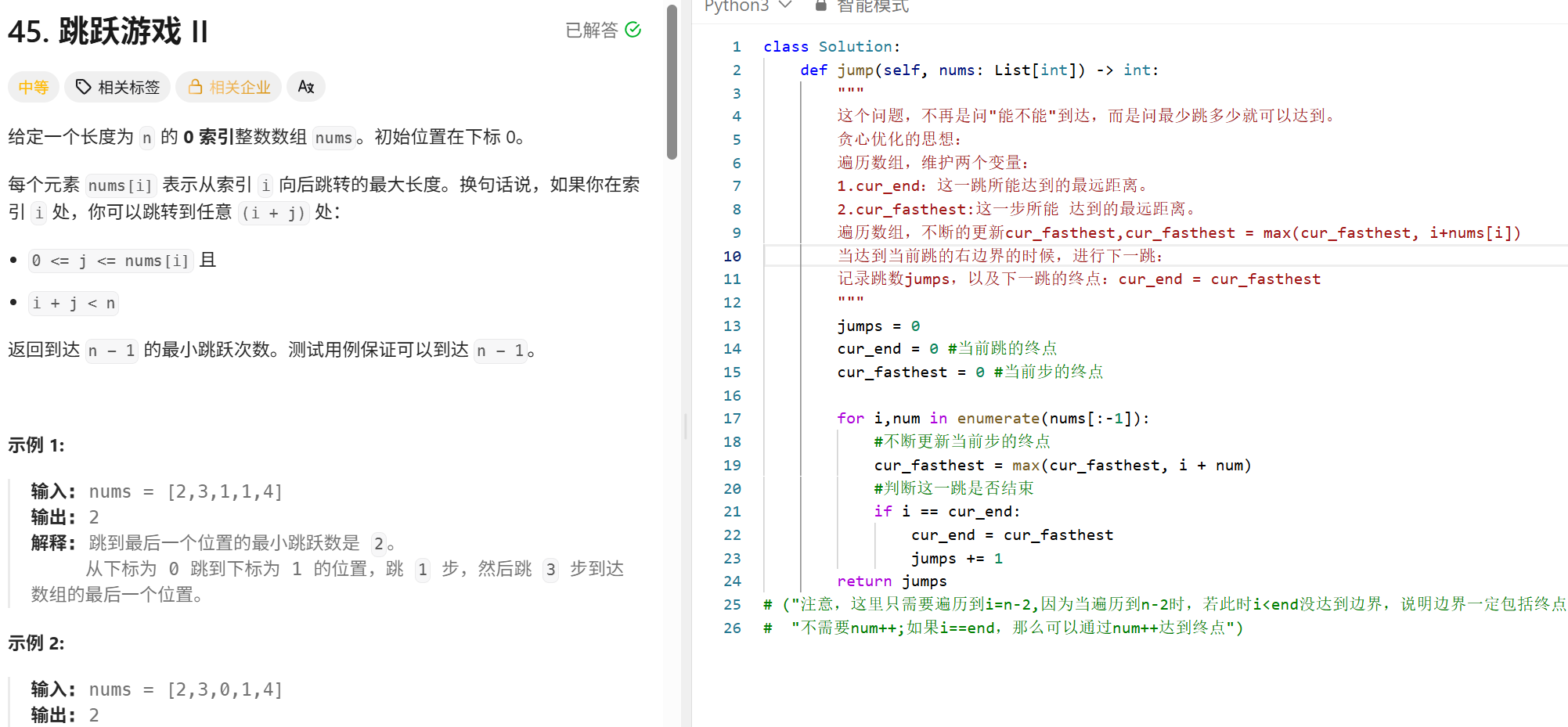
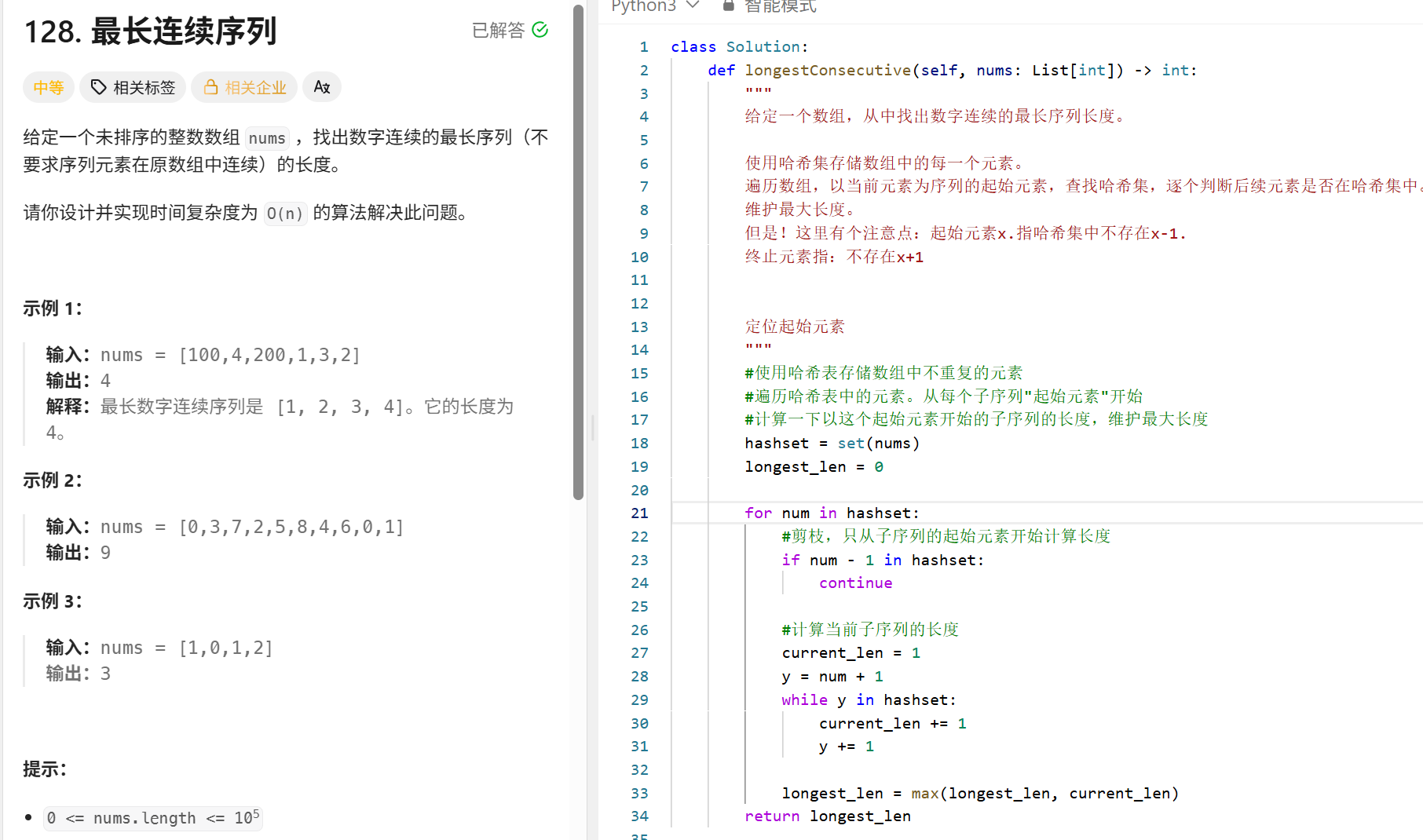
最长连续子序列 （哈希）

"""
使用哈希表来存储列表中的每一个元素，做到O(1)的查找时间
对最长连续序列的起始位置进行定位：
起始元素num：哈希表中不存在num-1
终止元素：哈希表中不存在num+1

时间复杂度：外层遍历去重后的每一个元素O(n)内层实现定位；只对序列的起始元素进行查找O(n)实现O(N)的复杂度
"""
class Solution:
    def longestConsecutive(self, nums: List[int]) -> int:
        """
        对于当前元素x，逐个判断后序x+1,x+2..是否是列表中，维护最大长度。
        优化：
        使用hash集存储列表中的元素。
        遍历hash集，定位最长连续序列的起始位置：
            对于当前元素x：
                若x-1在hash集中，则continue（当前元素不是最长连续序列的起始位置）
                否则，就逐渐判断后序元素是否在hash集中。
                维护最大长度
        """
        longest_list=0
        hashset=set(nums)
        for num in hashset: #!!!注意这里是遍历哈希表，需要去重
            current_length=1
            if num-1 in hashset:
                continue
            y=num+1
            while y in hashset:
                y+=1
                current_length+=1
            longest_list=max(longest_list,current_length)
        return longest_list

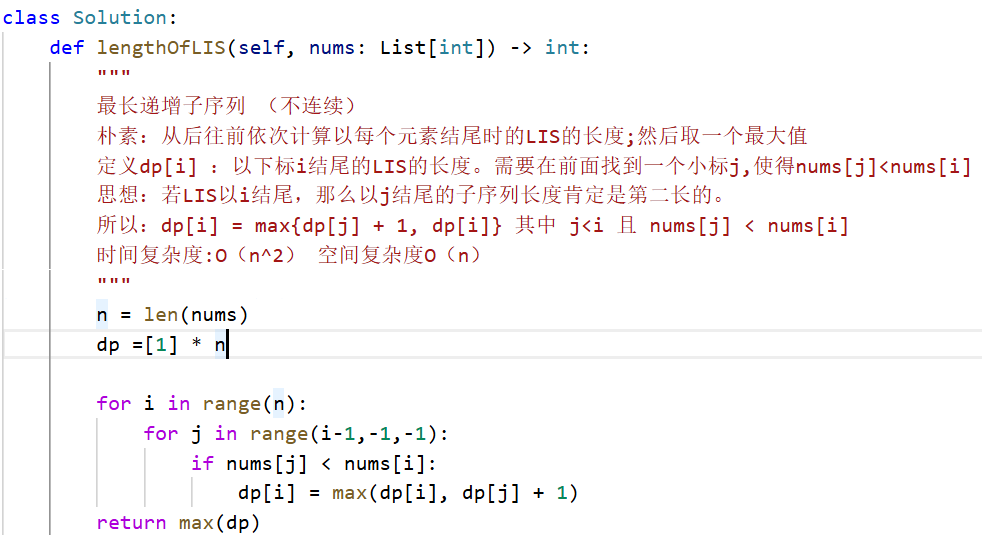
最长递增子序列（dp / 贪心+二分）

from functools import cache
from typing import List

"""

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列

思考：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 

考虑枚举方法：
从最后一个数字开始挨个枚举，考虑以当前数字结尾时的递增子序列的长度，取一个最大值即可。
假设 nums[i]是LIS的最后一个值，那么现在要到前面找到第一个比他小的值：
找到nums[j],使得j<i 且nums[j]<nums[i]

考虑子问题：如果nums[i]确实是 ”最长“递增子序列的最后一个值，那么nums[j]就必须是”最长“递增子序列的倒数第二个值，

以i结尾的最长递增子序列的长度=以j结尾的最长递增子序列 +1
即dfs(i)=max{dfs(j)}+1    j<i 且nums[j]<nums[i]
"""

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        n=len(nums)
        #表示以i即为的递增子序列的长度
        @cache
        def dfs(i):
            maxlen=0
            for j in range(i-1,-1,-1):
                if nums[j]<nums[i]: #注意这里是严格递增，所以是< 否则是<=
                        maxlen=max(maxlen,dfs(j)+1)
            return maxlen

        return max(dfs(i)+1 for i in range(n))

#时间复杂度：状态个数*每个状态的时间 O(n)*O(n)=O(n^2)
#空间复杂度：O(n)

"""
2.记忆化搜索改成递推：
即dfs(i)=max{dfs(j)}+1    j<i 且nums[j]<nums[i]
变为：
f[i]=max{f[j]}+1   j<i 且nums[j]<nums[i]
最后 max(f)
"""
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        n=len(nums)
        f=[1]*n
        #枚举每个值结尾时的递增子序列的长度
        for i in range(n):
            for j in range(i-1,-1,-1):
                if nums[j] < nums[i]:
                    f[i]=max(f[j]+1,f[i]) #f[i]=max{f[j]}+1 注意这里的j是个范围，所以要跟上一个值比较，
        return max(f)


from typing import List


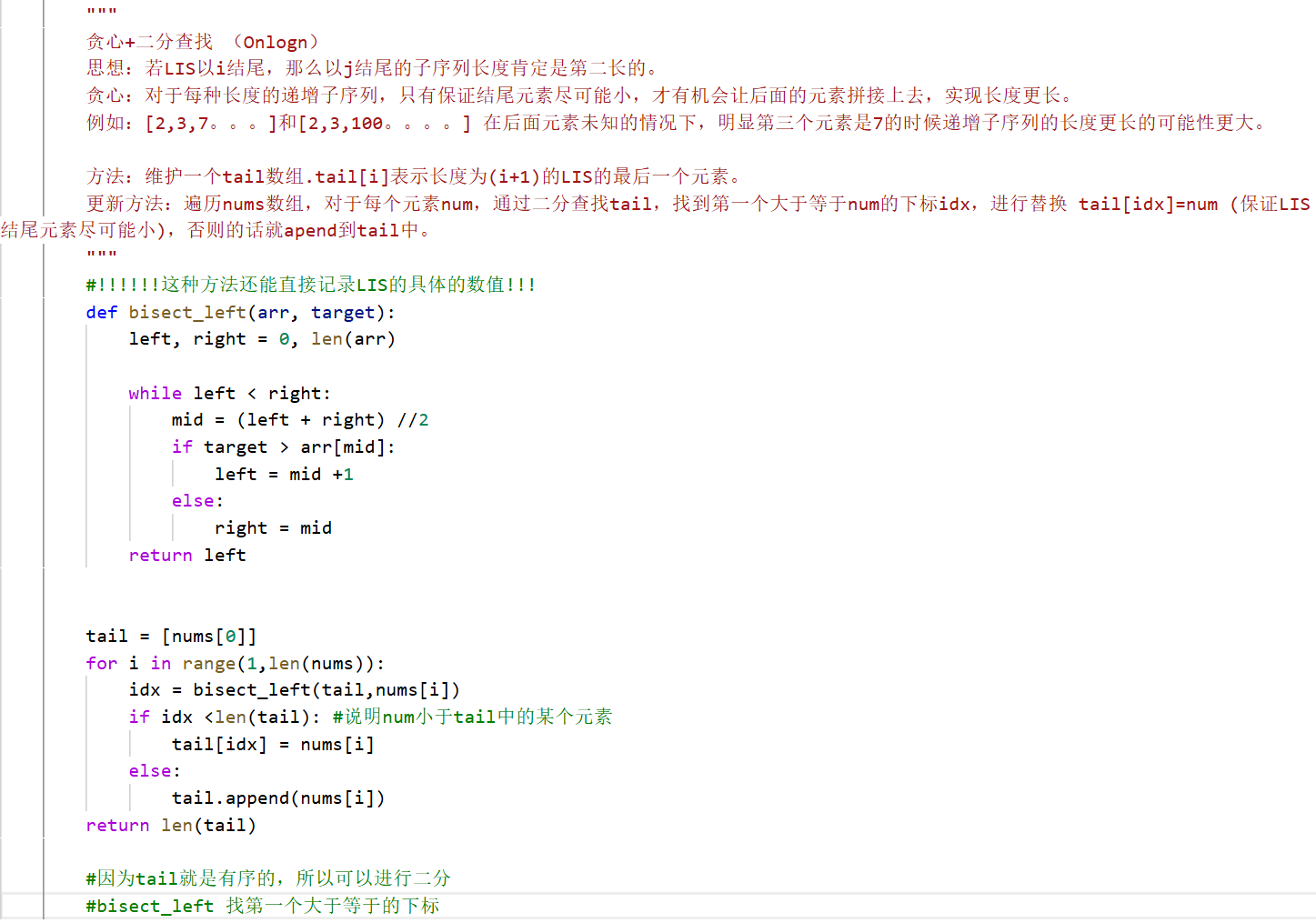
# 最长递增子序列，贪心+二分查找
""" 
贪心+二分查找 （Onlogn）
思想：若LIS以i结尾，那么以j结尾的子序列长度肯定是第二长的。
贪心：对于每种长度的递增子序列，只有保证结尾元素尽可能小，才有机会让后面的元素拼接上去，实现长度更长。
例如：[2,3,7。。。]和[2,3,100。。。。] 在后面元素未知的情况下，明显第三个元素是7的时候递增子序列的长度更长的可能性更大。

方法：维护一个tail数组.tail[i]表示长度为(i+1)的LIS的最后一个元素。
更新方法：遍历nums数组，对于每个元素num，通过二分查找tail，找到第一个大于等于num的下标idx，进行替换 tail[idx]=num (保证LIS结尾元素尽可能小)，否则的话就apend到tail中。
"""
class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        #!!!!!!这种方法还能直接记录LIS的具体的数值!!!
        def bisect_left(arr, target):
            left, right = 0, len(arr)

            while left < right:
                mid = (left + right) //2
                if target > arr[mid]:
                    left = mid +1
                else:
                    right = mid
            return left

        tail = [nums[0]]
        for i in range(1,len(nums)):
            idx = bisect_left(tail,nums[i])
            if idx <len(tail): #说明num小于tail中的某个元素
                tail[idx] = nums[i]
            else:
                tail.append(nums[i])
        return len(tail)

        #因为tail就是有序的，所以可以进行二分
        #bisect_left 找第一个大于等于的下标

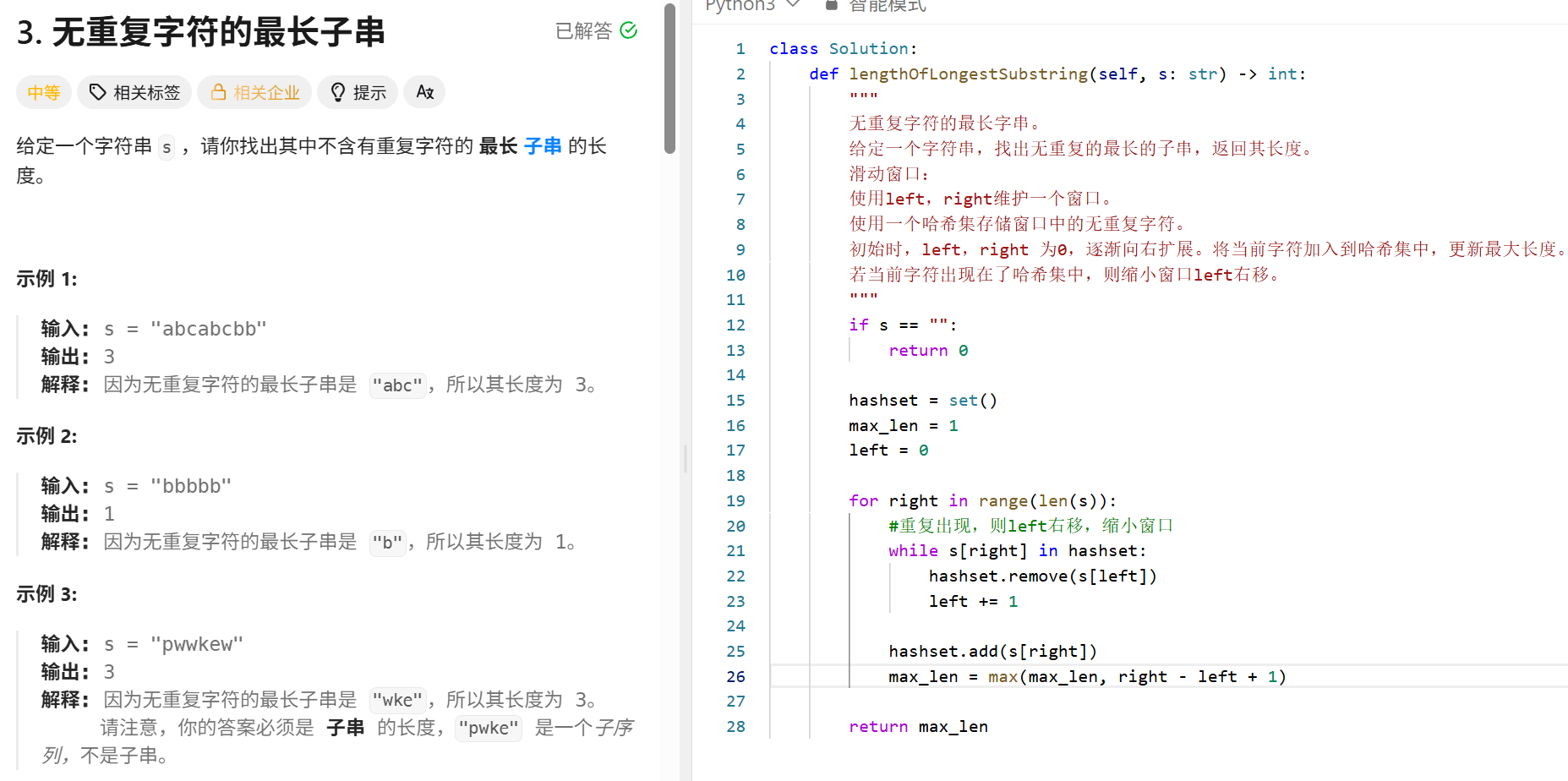
无重复字符的子长字串 (滑动窗口)

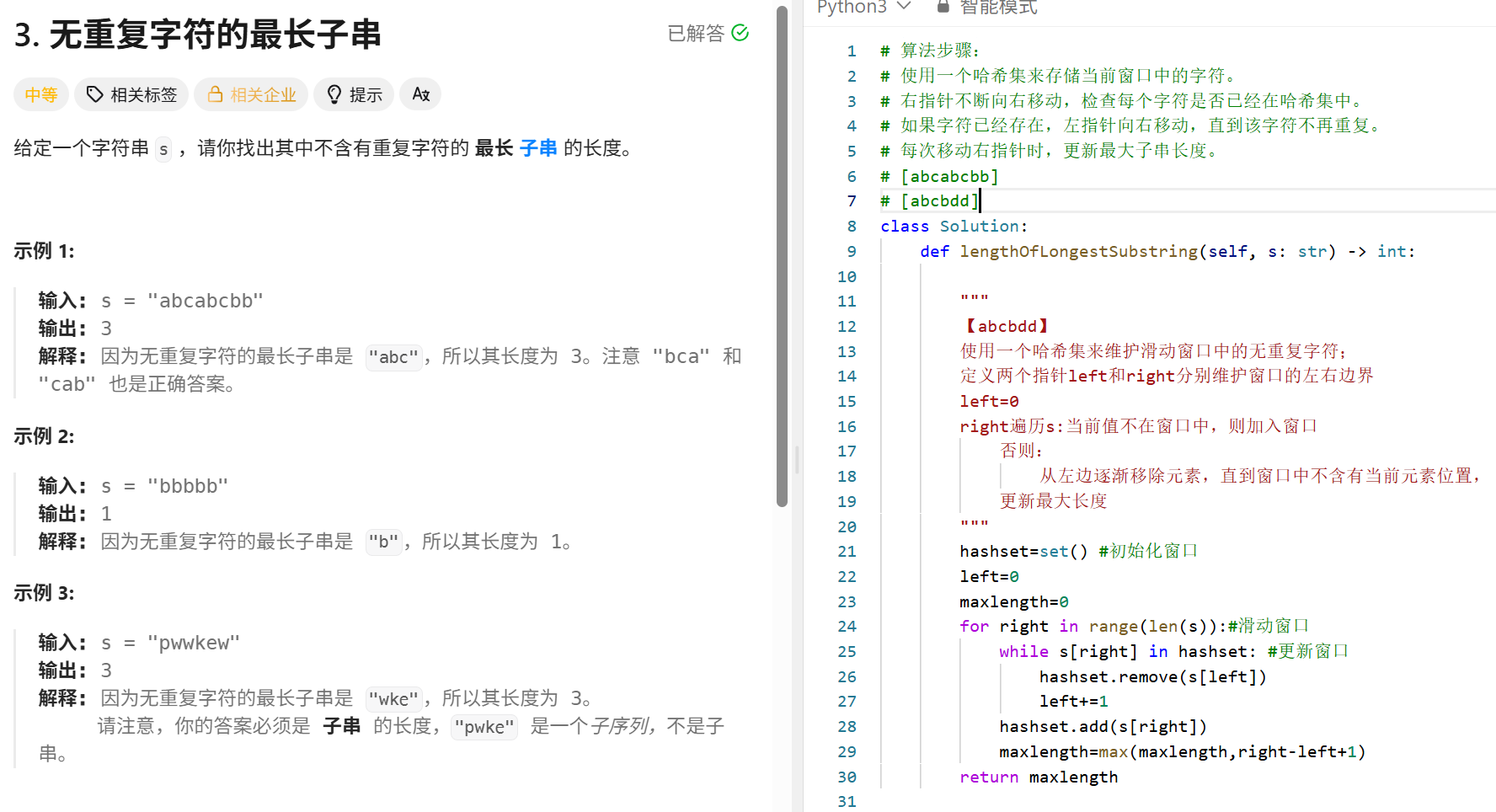
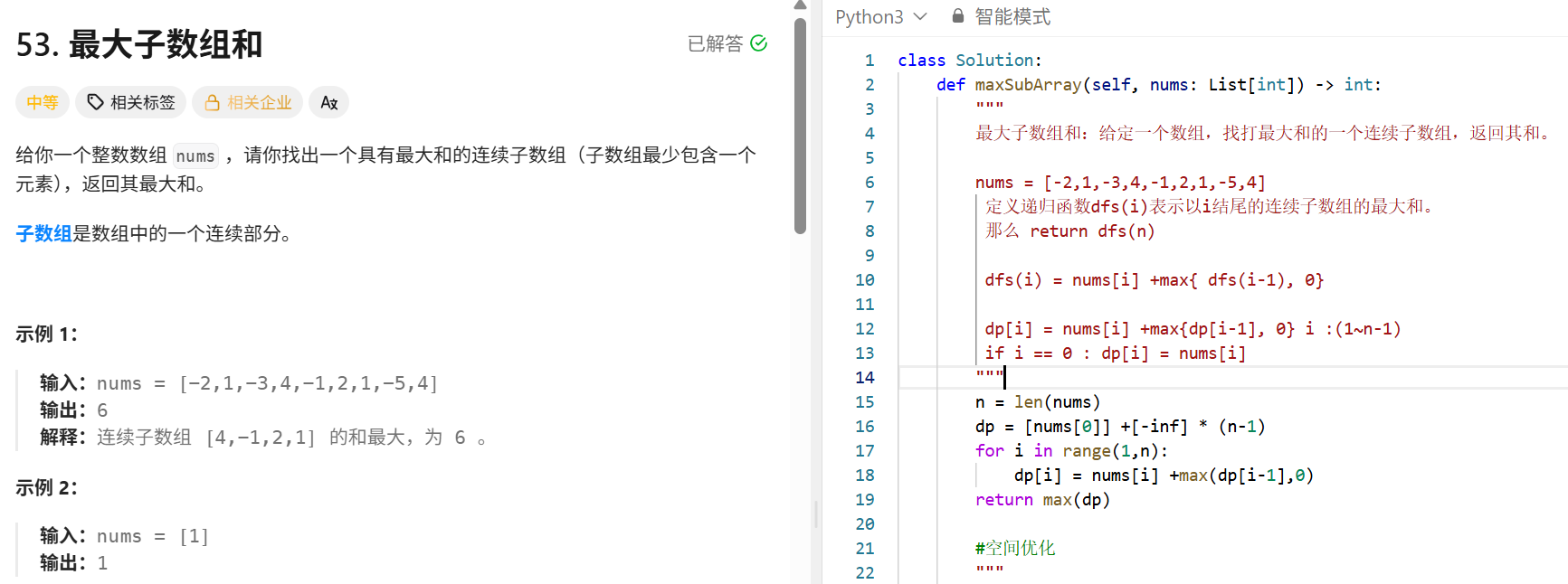
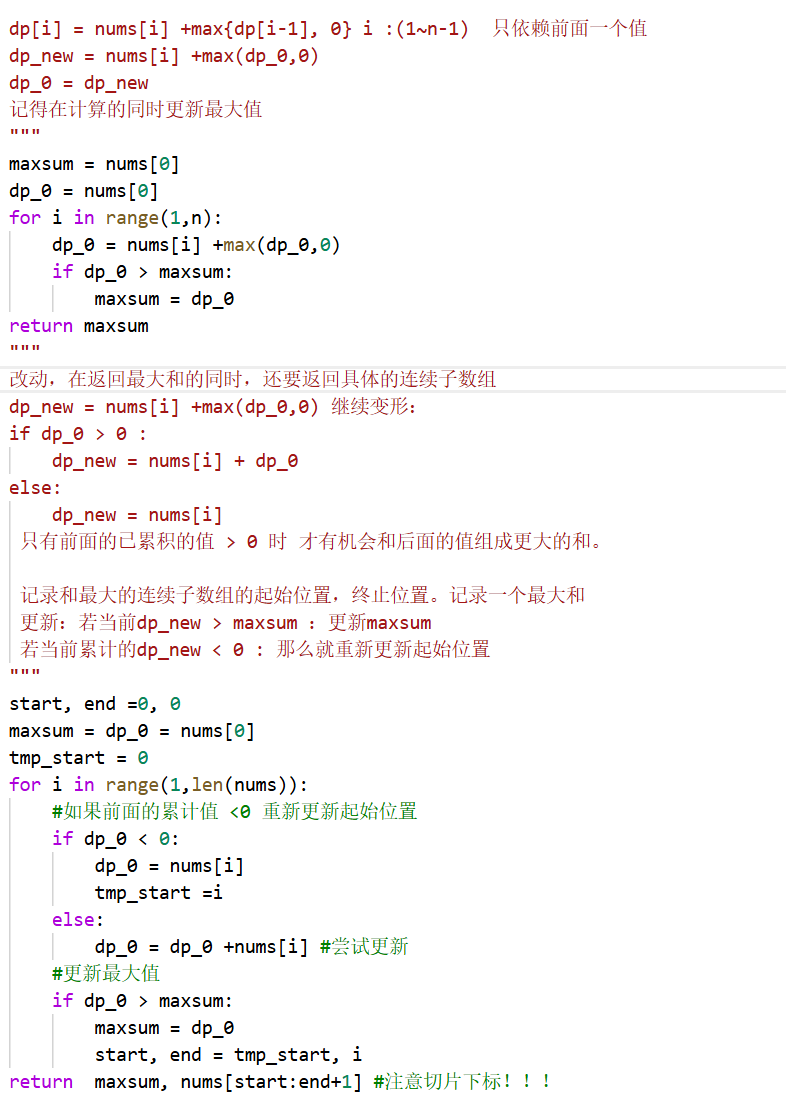
最大子数组和：(dp)

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        """
        最大子数组和：
        给定一个数组，要求返回和最大的子数组的和，以及具体的子数组。
        ⭐贪心：
        记录一个当前子数组的和变量cur_sum,最大子数组的和变量max_sum
        遍历数组，尝试将当前每一个值加入到cur_sum里面。
        if cur_sum < 0:说明当前值只会连累最终结果，应该从当前值重新累积。
        然后每一步都需要跟max_sum进行比较，记录最终的起始位置和结束位置 
        """
        start = 0
        cur_sum = nums[0]
        max_sum = cur_sum
        best_start = best_end = 0

        for i in range(1,len(nums)):
            if cur_sum < 0:
                #重新累计
                cur_sum = nums[i]
                start = i
            else:
                cur_sum += nums[i]
            
            #更新最大值
            if cur_sum > max_sum:
                max_sum = cur_sum
                best_start = start
                best_end = i
        return max_sum
        """
        动态规划的思路：
        定义动态规划方程 dp[i]表示以i结尾的最大子数组的和。
        dp[i] = nums[i] + max{dp[i-1], 0}
        既然是以i结尾，肯定包括nums[i]；"最大"：还要看一下前面是不是正数
        """
        n = len(nums)
        dp = [nums[0]] +[float("-inf")] * (n-1)

        for i in range(1,n):
            dp[i] = nums[i] + max(dp[i-1],0)
        return max(dp)

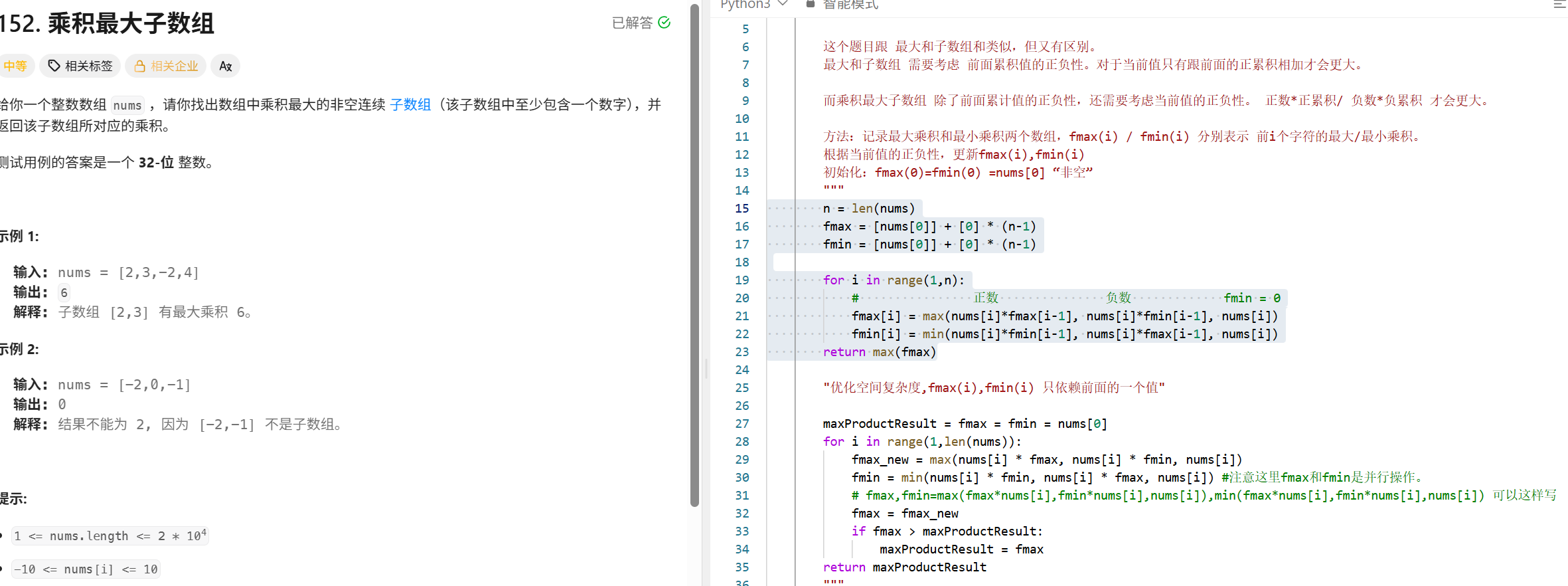
乘积最大子数组 (dp)

这个题跟上面的最大和的还是有点区别的。最大和只需要考虑是否是负数的情况。
而对于乘积来说，当遇到一个负数的时候，只有跟前面的最小子数组相乘的有可能得到更大的子数组。
例如：
[-2 3 -4]
如果只计算最大乘积子数组：
-2 
-2 3
-2 3 -4
显然这样是不对的。
正确过程应该考虑当前值的正负性，然后考虑到底跟最大的相乘还是跟最小的相乘。
[-2 3 -4]
最小子数组
-2
-2 -6
-2 -6 24

这里需要维护两个数组：
fmax(i)表示以i结尾的最大乘积子数组的值。
fmin(i)表示以i结尾的最小乘积子数组的值。
其中：
              正数               负数               前面是0的情况
fmax(i)=max{nums[i]*fmax(i-1),nums[i]*fmin(i-1),nums[i]}
fmin(i)=min{nums[i]*fmin(i-1),nums[i]*fmax(i-1),nums[i]}
初始条件，子数组只有一个字符：fmax[i]=fmin[i]=nums[i]
"""
# 乘积最大子数组
class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        n=len(nums)
        fmax=[0]*n
        fmin=[0]*n
        fmin[0]=fmax[0]=nums[0]
        for i in range(1,n):
            fmax[i]=max(fmax[i-1]*nums[i],fmin[i-1]*nums[i],nums[i])
            fmin[i] = max(fmax[i - 1] * nums[i], fmin[i - 1] * nums[i], nums[i])
        return max(fmax)

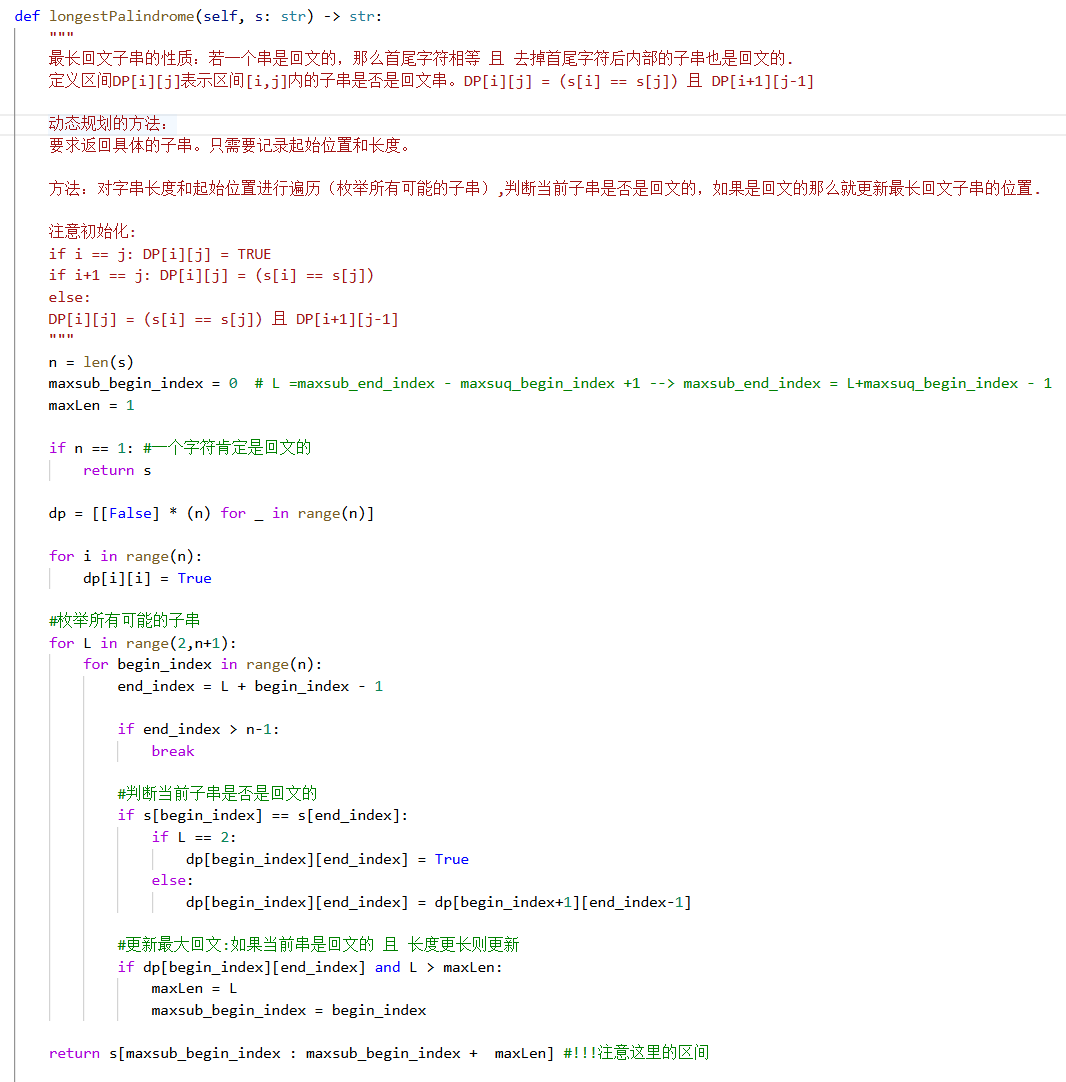
最长回文子串 （dp,中心扩展）

class Solution:
    def longestPalindrome(self, s: str) -> str:
        """
        最长回文子串的性质：若一个串是回文的，那么首尾字符相等 且 去掉首尾字符后内部的子串也是回文的.
        定义区间DP[i][j]表示区间[i,j]内的子串是否是回文串。DP[i][j] = (s[i] == s[j]) 且 DP[i+1][j-1]
        
        动态规划的方法：
        要求返回具体的子串。只需要记录起始位置和长度。

        方法：对字串长度和起始位置进行遍历（枚举所有可能的子串）,判断当前子串是否是回文的，
        如果是回文的那么就更新最长回文子串的位置.

        注意初始化:
        if i == j: DP[i][j] = TRUE
        if i+1 == j: DP[i][j] = (s[i] == s[j])
        else:
        DP[i][j] = (s[i] == s[j]) 且 DP[i+1][j-1]
        """
        n = len(s)
        maxsub_begin_index = 0  # L =maxsub_end_index - maxsuq_begin_index +1 --> maxsub_end_index = L+maxsuq_begin_index - 1
        maxLen = 1

        if n == 1: #一个字符肯定是回文的
            return s
        
        dp = [[False] * (n) for _ in range(n)]

        for i in range(n):
            dp[i][i] = True
        
        #枚举所有可能的子串
        for L in range(2,n+1):
            for begin_index in range(n):
                end_index = L + begin_index - 1
                
                if end_index > n-1:
                    break

                #判断当前子串是否是回文的
                if s[begin_index] == s[end_index]:
                    if L == 2:
                        dp[begin_index][end_index] = True
                    else:
                        dp[begin_index][end_index] = dp[begin_index+1][end_index-1]
                
                #更新最大回文:如果当前串是回文的 且 长度更长则更新
                if dp[begin_index][end_index] and L > maxLen:
                    maxLen = L
                    maxsub_begin_index = begin_index

        return s[maxsub_begin_index :  maxsub_begin_index + maxLen] #!!!注意这里的区间

        """
        中心扩展的方法：
        动态规划的方法是 枚举所有可能长度的回文串并判断是否回文。
        当前方法是 枚举所有可能的回文中心，并尝试向外进行扩展,记录每个回文中心扩展出来的最长长度。

        若中心是回文的，且边界可扩展（s[i] == s[j]） 那么有理由相信向外扩展后的串也是回文的。

        回文中心:
            奇数: aba :中心是单个字符
            偶数： abba :中心是两个相邻的字符
        """

        n = len(s)
        maxsub_begin_index = 0
        maxLen = 1
        
        def expandcenter(s, cen_i, cen_j):
            #尝试向外扩展
            while cen_i >= 0 and cen_j < n and s[cen_i] == s[cen_j]:
                cen_i -= 1
                cen_j += 1

            return cen_i+1, cen_j-1

        #枚举所有中心
        for i in range(n):
            #获取当前中心扩展后的最长回文子串的左右边界
            #奇数情况下
            left1, right1 = expandcenter(s, i, i)
            #偶数情况下
            left2, right2 = expandcenter(s,i, i+1)

            #更新最长回文子串的长度
            if right1 - left1 + 1> maxLen:
                maxsub_begin_index = left1
                maxLen = right1 - left1 + 1

            if right2 - left2 + 1> maxLen:
                maxsub_begin_index = left2
                maxLen = right2 - left2 + 1

        return s[maxsub_begin_index : maxsub_begin_index + maxLen]

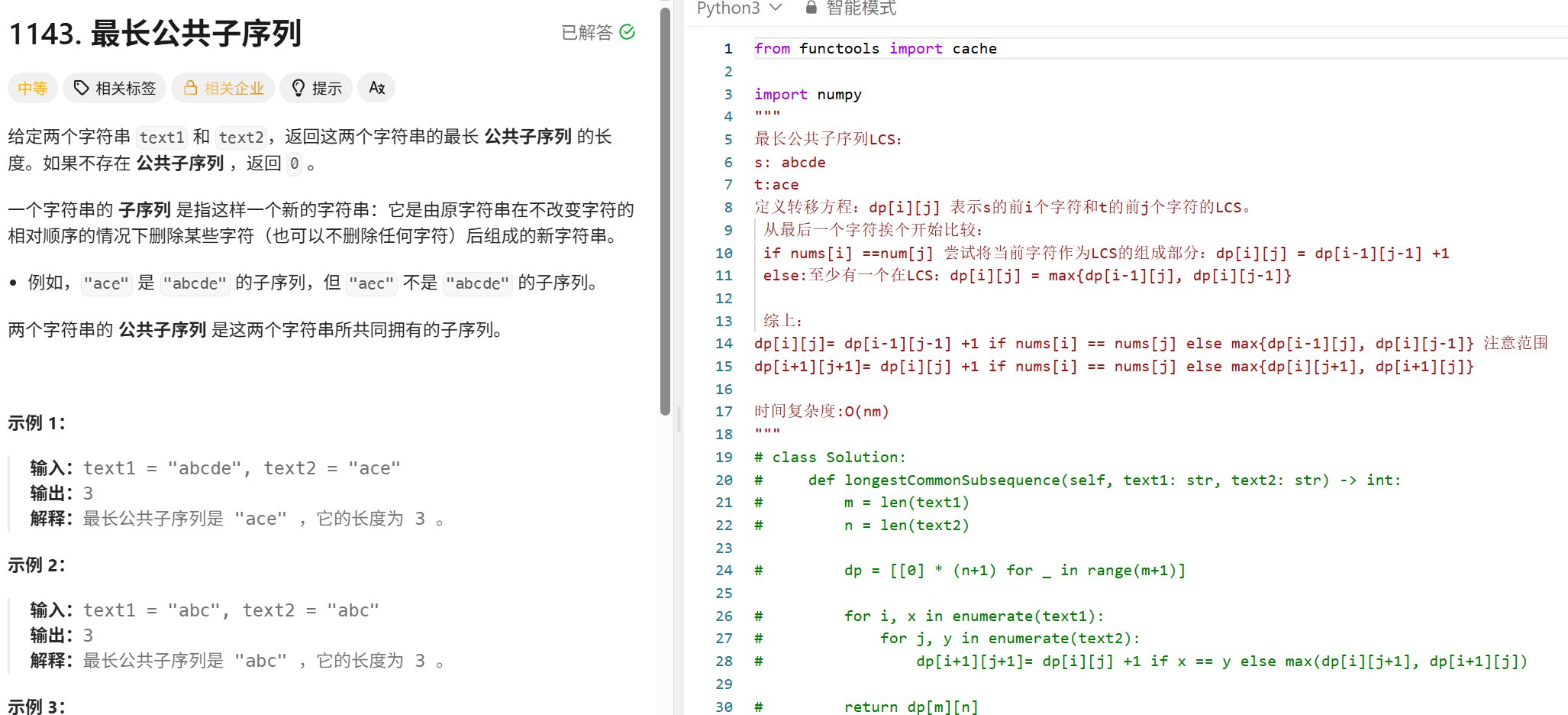
最长公共子序列

from functools import cache

import numpy
"""
最长公共子序列LCS：
s: abcde
t:ace
定义转移方程：dp[i][j] 表示s的前i个字符和t的前j个字符的LCS。
 从最后一个字符挨个开始比较：
 if nums[i] ==num[j] 尝试将当前字符作为LCS的组成部分：dp[i][j] = dp[i-1][j-1] +1
 else:至少有一个在LCS：dp[i][j] = max{dp[i-1][j], dp[i][j-1]}

 综上：
dp[i][j]= dp[i-1][j-1] +1 if nums[i] == nums[j] else max{dp[i-1][j], dp[i][j-1]} 注意范围
dp[i+1][j+1]= dp[i][j] +1 if nums[i] == nums[j] else max{dp[i][j+1], dp[i+1][j]}

时间复杂度:O(nm)
"""
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        m = len(text1)
        n = len(text2)

        dp = [[0] * (n+1) for _ in range(m+1)]

        for i, x in enumerate(text1):
            for j, y in enumerate(text2):
                dp[i+1][j+1]= dp[i][j] +1 if x == y else max(dp[i][j+1], dp[i+1][j])
    
        return dp[m][n]
"""
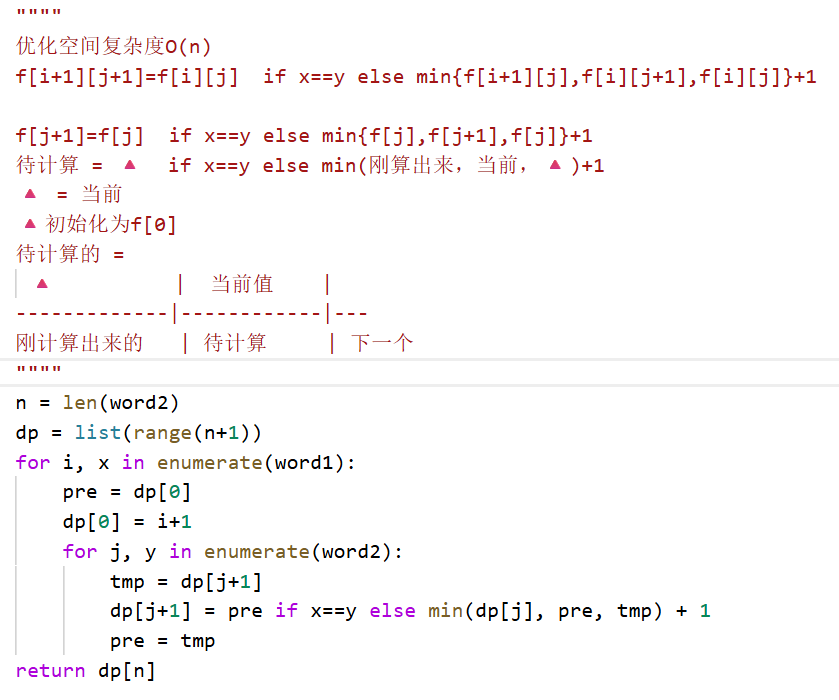
时间复杂度优化：O（n+1）
dp[i+1][j+1]= dp[i][j] +1 if x == y else max{dp[i][j+1], dp[i+1][j]}
dp[j+1]= dp[j] +1 if x == y else max{dp[j+1], dp[j]}

当前值待计算的值 依赖于 上一行左列的值， 左边刚刚计算出来的值，当前值。
当前待计算的值 = 🔺+1 if x == y else max{刚计算出来的值，当前值}
🔺 = 当前值

🔺         |   当前值      |
------------|---------------|----- 
刚计算出来的  |  带计算的值   |下一个计算的

🔺初始化为当前行第一个值（0）因为dp[i][0] = 0
"""
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        n = len(text2)
        dp = [0] * (n+1)

        for x in text1:
            pre = 0 
            for j, y in enumerate(text2):
                当前值 = dp[j+1]
                dp[j+1]= pre +1 if x == y else max(当前值, dp[j])
                pre = 当前值
        return dp[n]

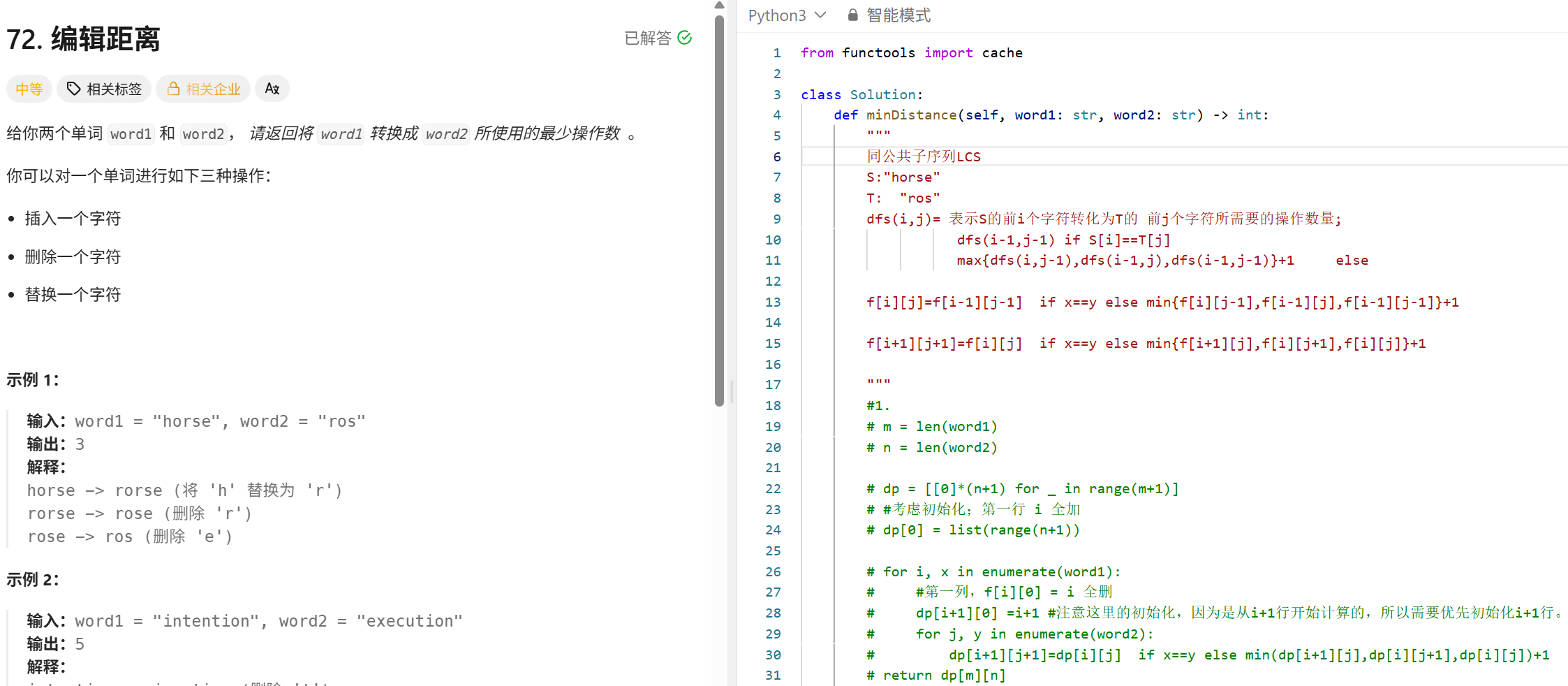
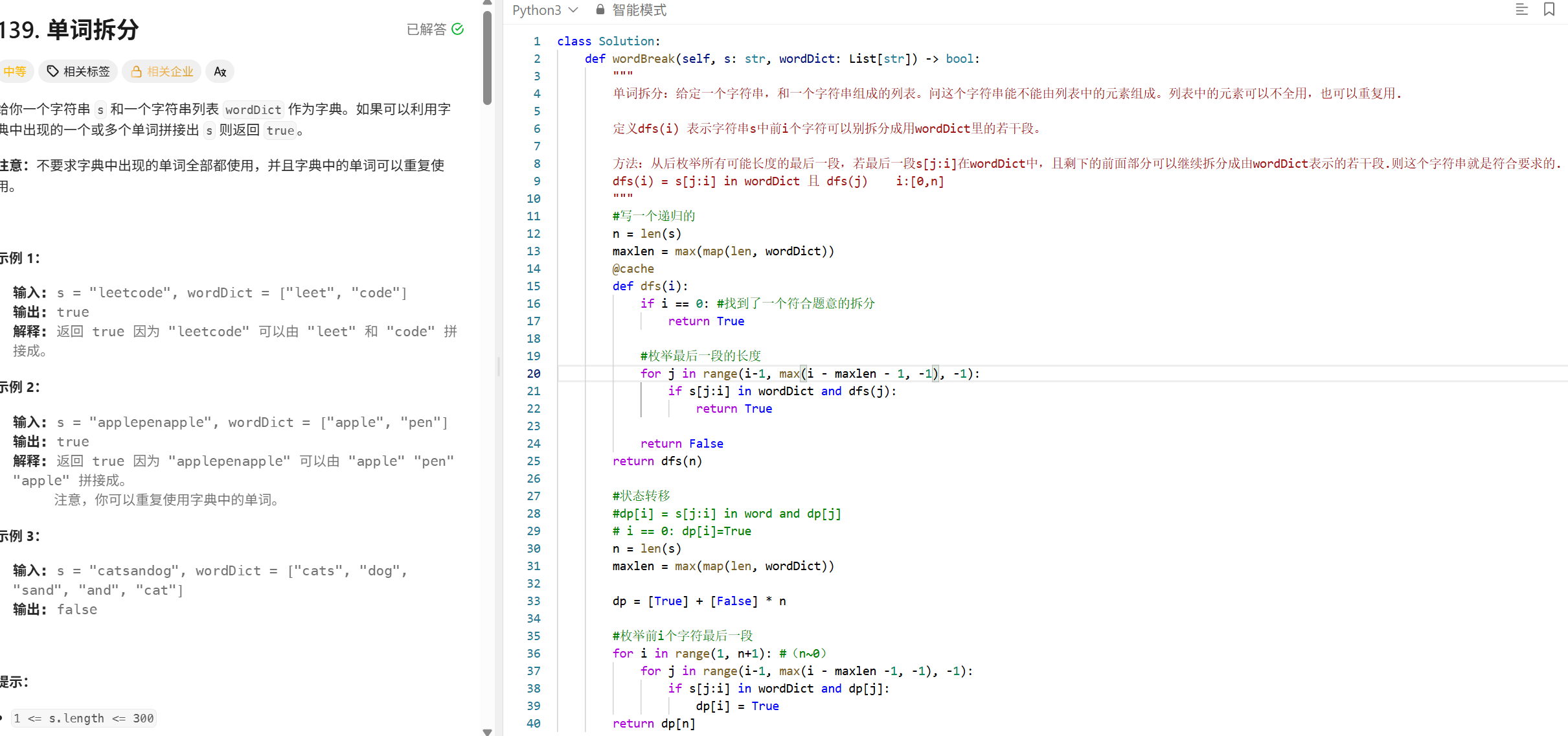
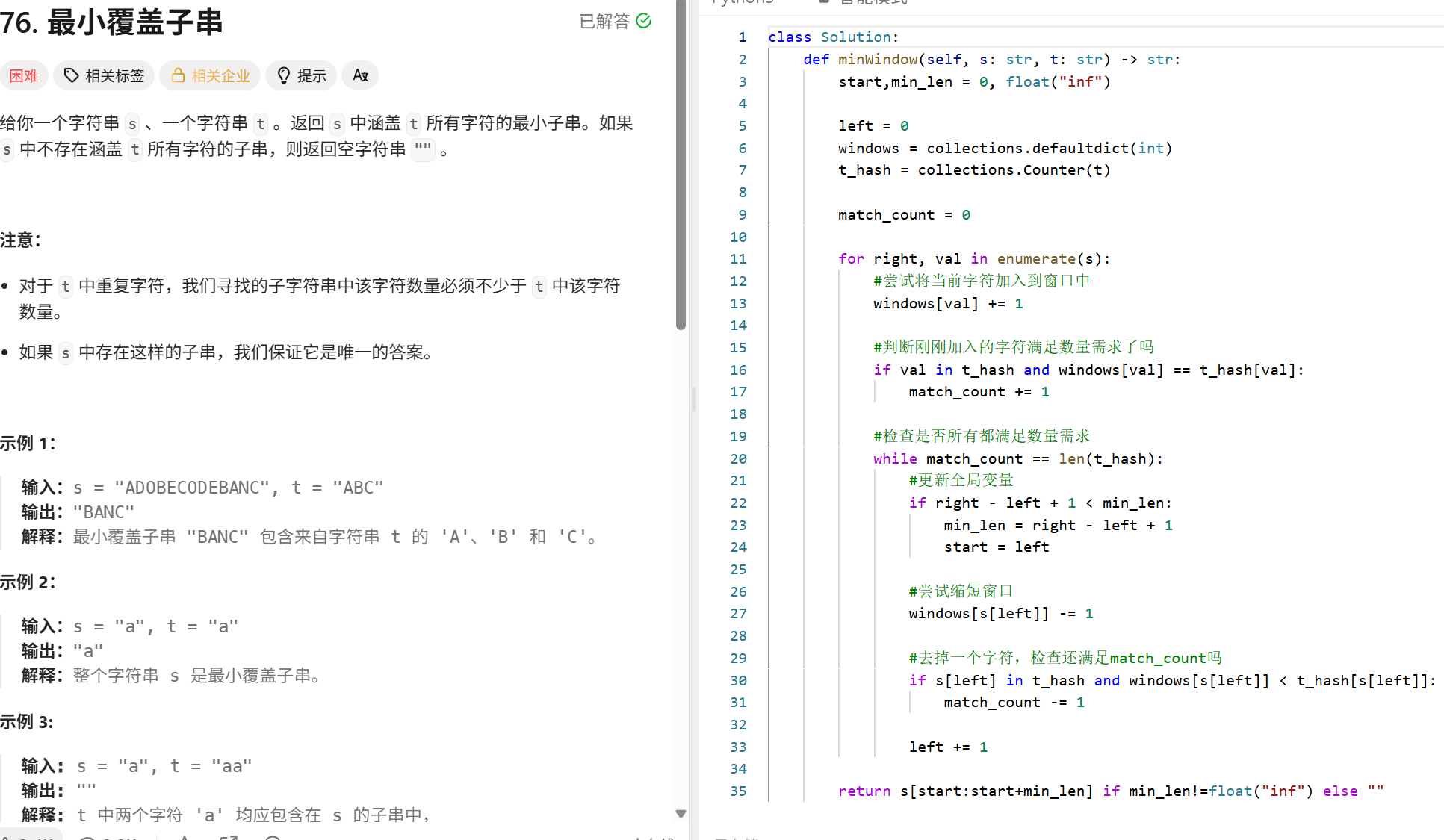
最小覆盖字串

图论：

并查集的思路
class UnionFind:
    def __init__(self,grid):
        row = len(grid)
        col = len(grid[0])

        self.root = [-1] * (row*col)
        self.land = 0
        #root数组初始化，记录陆地数量
        for r in range(row):
            for c in range(col):
                if grid[r][c] == "1":
                    #因为只会对陆地进行合并，所以不需要管水"0"的值是多少
                    self.root[r*col+c] = r*col+c
                    self.land += 1
    #查找
    def Find(self,x):
        if self.root[x] == x:
            return x
        else:
            self.root[x] = self.Find(self.root[x])
            return self.root[x]
    #合并
    def Union(self,x,y):
        rootx = self.Find(x)
        rooty = self.Find(y)
        if rootx != rooty:
            self.root[rootx] = rooty
            #陆地-合并次数
            self.land -= 1
    #返回最终的岛屿数量
    def getCount(self):
        return self.land

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        """
        岛屿数量：给定一个由1和0组成的二维网格。
        要求求岛屿的数量。岛屿是被水包围的陆地的连接。
        岛屿的数量 = 陆地的数量总和 - 联通操作的次数.
        使用并查集，将二维矩阵转化为一维的root数组，初始化的同时记录陆地的数量。
        在union操作函数中记录 合并的次数。最后返回陆地数量-合并数量.
        """
        #从左上角依次遍历，遇到"1"对其上下左右进行搜索并进行合并操作。最后返回getcount

        if grid is None or len(grid) == 0:
            return 0
        uf = UnionFind(grid)
        
        row = len(grid)
        col = len(grid[0])

        for i in range(row):
            for j in range(col):
                if grid[i][j] == "1":
                    for x,y in[(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:
                        if 0 <= x < row and 0 <= y < col and grid[x][y] == "1":
                            uf.Union(col*i+j,col*x+y)
        return uf.getCount()

广度优先遍历的思路：
class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        """
        岛屿数量BFS
        遍历网格中的每一个元素，如果当前元素是"1"说明找到了一个岛屿，result+1；将当前网格放入到队列中，
        循环队列不空：以当前网格(i,j)为岛屿的起点，进行上下左右四个方向搜索相邻的陆地，把他们都做上标记，并放到队列中。

        （result记录的是岛屿起点的数量. 有多少个不同的起点，就有多少岛屿
        """
        row = len(grid)
        col = len(grid[0])
        queue = collections.deque()
        result = 0

        for r in range(row):
            for c in range(col):
                if grid[r][c] == "1":
                    grid[r][c] = "*"
                    result += 1 #表示找到了一个岛屿
                    queue.append((r,c))

                    #循环队列，进行搜索
                    while queue:
                        i,j = queue.popleft()
                        #对其上下左右进行搜索
                        for x, y in [(i-1,j),(i+1,j),(i,j-1),(i,j+1)]:
                            if 0 <= x < row and 0 <= y < col and grid[x][y] == "1":
                                grid[x][y] = "*"
                                queue.append((x,y))
        return result 
        
深度优先遍历的思想：
class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        # DFS 以当前格子为起点，进行上下左右dfs深度搜索
        row = len(grid)
        col = len(grid[0])
        result = 0

        def dfs(i,j):
            if i < 0 or j < 0 or i >= row or j >= col or grid[i][j] !="1":
                return

            #做标记
            grid[i][j] = "0"

            dfs(i-1,j)
            dfs(i+1,j)
            dfs(i,j-1)
            dfs(i,j+1)

        for i in range(row):
            for j in range(col):
                if grid[i][j] == "1": #起点进行dfs
                    result += 1

                    dfs(i,j)

        return result

class Solution:
    def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
        """
        课程表：给定选修的课程总数，以及课程之间选修的顺序关系。
        判断是否能够按照这个规则选修完所有的课程。
        拓扑排序：判断有向图中是否存在环路。如果有环就说明不能按要求修完。
        拓扑排序：
        定义 入度表 和 有向表。
        初始时，将入度为0的节点入队列。
        循环队列：
        取出队头元素，记录删掉的节点数量。将相连的节点入度-1.
        若入度减到0，那么入队列。
        最后判断删掉的节点数量是否跟有向图的节点数量一样.
        """
        #定义入度表 和 邻接表
        indrgree = [0 for _ in range(numCourses)]
        adjancey = [[] for _ in range(numCourses)] #n*n的矩阵,以每个元素的下标索引为值
        queue = collections.deque()

        count = 0

        for pre,cur in prerequisites: #cur -> pre
            indrgree[pre] += 1
            adjancey[cur].append(pre)
        
        #将入度为0的点放入队列
        for i,ind in enumerate(indrgree):
            if ind == 0:
                queue.append(i)
        #循环队列，取出，相邻入度-1
        while queue:
            pre = queue.popleft()
            count += 1
            #相邻节点 入度-1
            for cur in adjancey[pre]:
                indrgree[cur] -= 1
                if indrgree[cur] == 0:
                    queue.append(cur)

        return count == numCourses

"""
前缀树（字典树）：26叉树。


节点结构:
1.指向孩子节点的指针(一个字典（孩子字符可能有26个选择）)，存储当前字符的后序所有可能的字符
2.一个结束标志位，表示是否以当前节点结尾。

2.inset 向前缀树插入字符串word：
 从根节点逐字符插入，如果当前字符不在子节点中，那么就创建一个新节点。最后一个节点is_end=True

3.查找：判断word是否在前缀树。
从根节点逐字符查找，查找完成且查找的最后一个节点的is_end=True

4.前缀匹配:判断前缀树中是否存在某个前缀 prefix
只要能够从根节点逐个匹配完成就返回true，没有is_end=True的条件
"""
class TrieNode:
    def __init__(self):
        self.children={} #以“a”字母开头的word的中第二个字母有26种选择；所以每个节点的子节点是一个长度为26的数组或者大小为26的字典。
        self.is_end=False

class Trie:
    def __init__(self):
        self.root=TrieNode() #根节点

    def insert(self,word)->None:#只是共用了前缀字符节点。
        node=self.root
        #从根节点开始逐字符插入
        for c in word:
            if c not in node.children:

                node.children[c]=TrieNode() #不在，就新建一个孩子节点
            node=node.children[c]
        node.is_end=True
    def search(self,word)->bool:
        node=self.root
        for c in word:
            if c not in node.children:
                return False
            node=node.children[c]
        return node.is_end

    def startWith(self,prefix)->bool:
        node=self.root
        for c in prefix:
            if c not in node.children:
                return False
        node = node.children[c]
        return True

class Solution:
    def solve(self, board: List[List[str]]) -> None:
        """
        把被包围的区域去掉。
        只有边界上的O以及与边界O上下左右相邻的O才是安全的。其他都是不安全的.
        方法：
        从边界开始，依次遍历边界上的O，使用DFS/BFS搜索上下左右相邻的O。
        将这些安全的O标记为#。
        然后从头重新遍历矩阵：
        if val == #:
            重置为O；
        elif val == O:
            重置为X
        """
        """DFS"""
        if not board or len(board) == 0:
            return 
        
        row = len(board)
        col = len(board[0])

        def dfs(r,c):
            #只对O进行搜索
            if r<0 or c<0 or r>=row or c>=col or board[r][c]!='O':#注意这个条件，排除X和#
                return
            
            board[r][c]="#"
            dfs(r+1,c)
            dfs(r-1,c)
            dfs(r,c-1)
            dfs(r,c+1)

        #遍历边界,标记O及其相邻区域
        for i in range(row):
            dfs(i,0)
            dfs(i,col-1)
        for j in range(1,col-1):
            dfs(0,j)
            dfs(row-1,j)
        
        #重新依次遍历，还原#,并删除不安全的区域O
        for i in range(row):
            for j in range(col):
                if board[i][j] == "#":
                    board[i][j] = "O"
                elif board[i][j] == "O":
                    board[i][j] = "X"
        """BFS"""
        queue = collections.deque()
        #依旧遍历边界，标记，存入队列
        if not board or len(board) == 0:
            return
        row, col = len(board), len(board[0])

        for i in range(row):
            if board[i][0] == "O":
                board[i][0] = "#"
                queue.append((i,0))
            if board[i][col-1] == "O":
                board[i][col-1] = "#"
                queue.append((i,col-1))
        for j in range(1,col-1):
            if board[0][j] =="O":
                board[0][j] = "#"
                queue.append((0,j))
            if board[row-1][j] == "O":
                board[row-1][j] = "#"
                queue.append((row-1,j))
        #循环队列，遍历
        while queue:
            r,c = queue.popleft()
            for x,y in [(r-1,c),(r+1,c),(r,c-1),(r,c+1)]:
                if 0<=x<row and 0<=y<col and board[x][y]=="O":
                    board[x][y]="#"
                    queue.append((x,y))

        #重新遍历，还原
        for i in range(row):
            for j in range(col):
                if board[i][j] == "#":
                    board[i][j] = "O"
                elif board[i][j] == "O":
                    board[i][j] = "X"

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        """
        01矩阵：给定一个由0，1组成的矩阵。
        输出一个相同大小的矩阵，矩阵中每个元素表示其到最近0的曼哈顿距离。
        方法：
        使用多源BFS；将所有的0作为BFS的起点，向四周层层扩展(步数+1)；
        那么每个格子第一次被访问到的层数就是它跟最近0的距离。
        具体：
        初始化目标矩阵：
            0元素的距离为0。
            1元素的距离初始化为inf。
        将0元素放到队列中。
        循环队列：
            取出队头元素，向四周扩展。
            如果邻居元素距离没有被更新，那么就更新
            即：if 邻居元素距离 > 当前元素距离 + 1：
                    更新邻居元素距离 = 当前元素距离 + 1
                    并将邻居元素入队列。
        """
        #初始化目标矩阵
        row, col = len(mat),len(mat[0])
        dist = [[float("inf")]*col for _ in range(row)]
        queue = collections.deque()

        #将0元素位置放到队列中，作为BFS的起点。
        for i in range(row):
            for j in range(col):
                if mat[i][j] == 0:
                    dist[i][j] = 0
                    queue.append((i,j))
        #循环队列，四周扩展搜索距离
        while queue:
            x,y = queue.popleft()
            #搜搜四周
            for i,j in [(x+1,y),(x-1,y),(x,y-1),(x,y+1)]:
                #当前位置的距离和邻居位置的距离比较
                if 0<=i<row and 0<=j<col:
                    if dist[i][j] > dist[x][y] + 1:
                        dist[i][j] = dist[x][y] + 1
                        queue.append((i,j))
        return dist

数学

"""
一个数字后面跟着的0的个数：比如100
暴力的想法就是 从末尾不断的mod10
while x mod 10 ==0:
 num++
x中末尾0的个数就是x中因子10的个数。

n!中尾随0的个数就是n!中所含因子10的个数，而10=2*5，一般来说5的因子个数要小于2.所以n!中尾随0的个数取决于因子5的个数。

对n!从末尾不断的 mod 5 并记录。
优化：即 [1~n]中每个数字中的因子5之和。
时间复杂度O(N)

优化：
从倍数的角度出发：

为了计算 n! 中 5 的因子的数量，我们需要考虑以下几点：
直接的 5 的倍数：例如，5、10、15、20 等，每个数都贡献一个 5 的因子。 （x有多少个5就至少有多少个因子5
更高次幂的 5 的倍数：例如，25 是 5平方，它贡献了两个 5 的因子；125 是 5的三次方，它贡献了三个 5 的因子。 

count=sigma(k=1->inf) [n/5^k]
时间复杂度优化O 

例如 n=25  即25！中尾随0的个数
(25*24*23*....)还是方法一的思想，挨个找每个数字中的因子5的个数。

[25/5]=5  (5，10，15，25)
[25/25]=1 (25)

直到5**k>n  -->k=math.floor(log_5 n)  所以复杂度是O(logn)
这样
"""

class Solution:
    def trailingZeroes(self, n: int) -> int:
        k=1
        count=0
        while True:
            if 5**k>n:
                break
            count += n//5**k
            k+=1

        return count

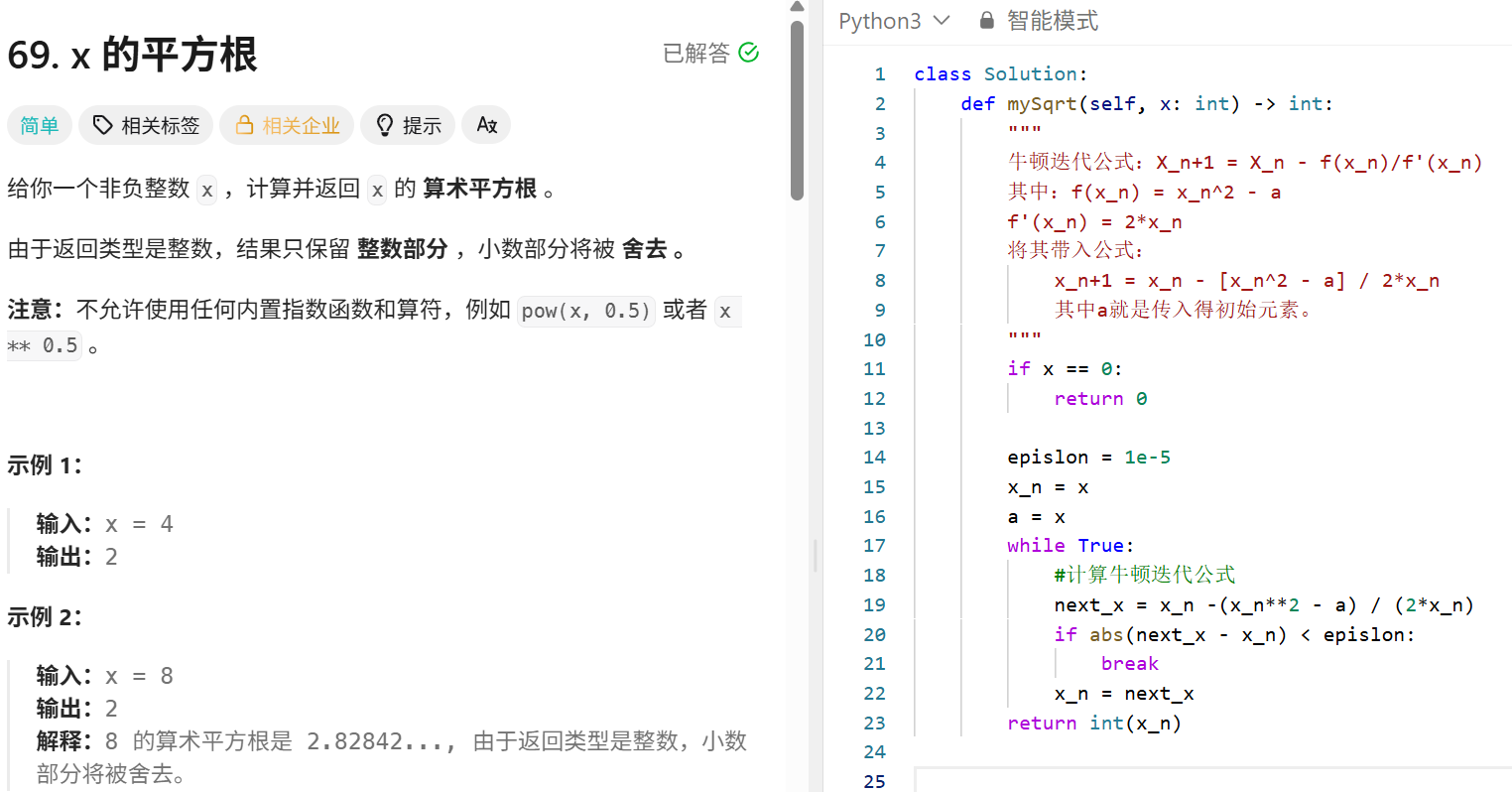
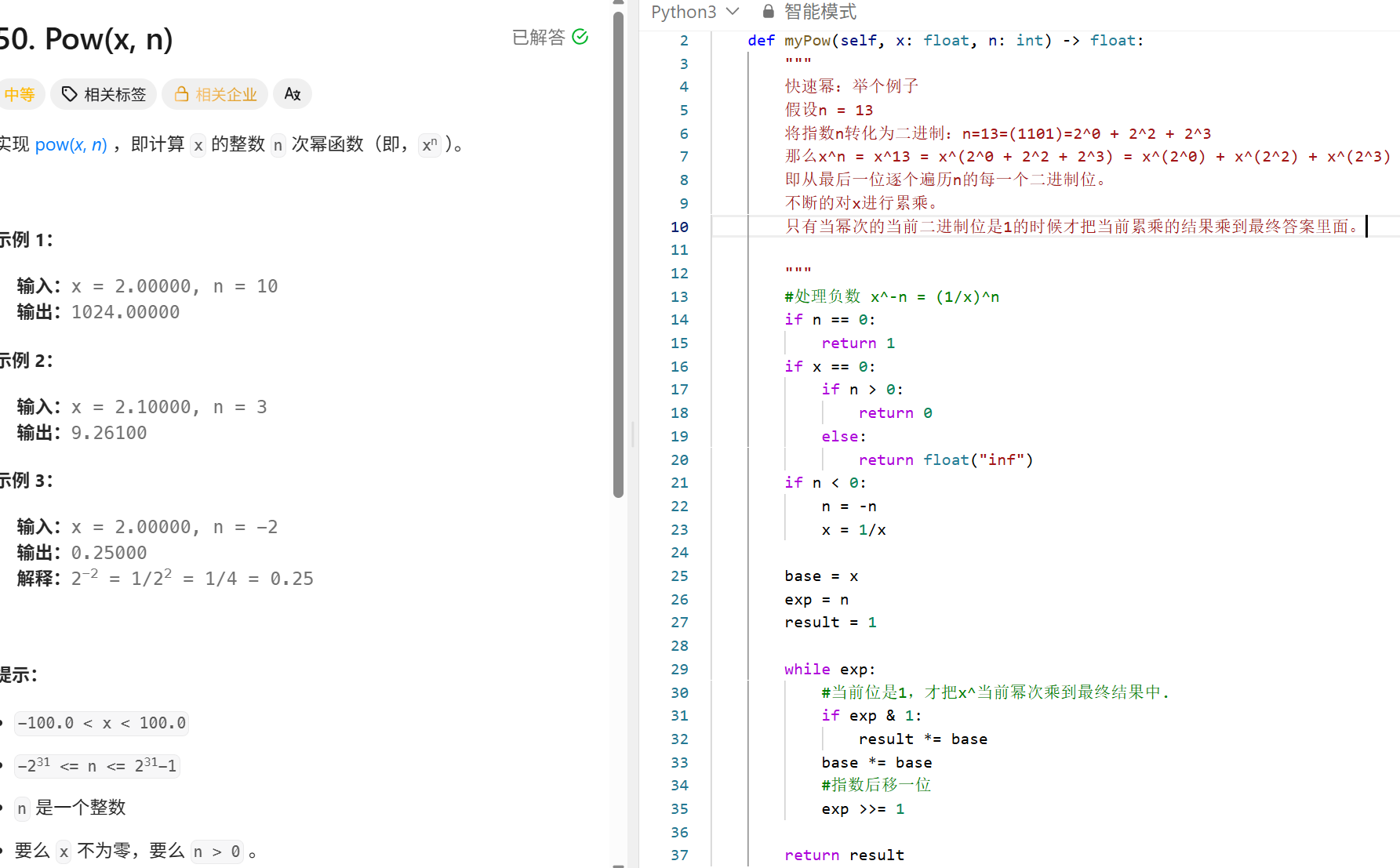
二叉树

二叉树前中后序遍历：

"""
二叉树的前序遍历：根左右。

"""
import collections
from typing import Optional, List


class TreeNode:
    def __init__(self,val,left,right):
        self.val=val
        self.left=left
        self.right=right

#递归版本
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        #注意判断root是否为空
        result=[]
        def preorder(root):
            #根左右
            if not root:
                return
            result.append(root.val)
            preorder(root.left)
            preorder(root.right)

        preorder(root)
        return result
#非递归版本：用栈来模拟递归的过程
"""
注意：栈是后进先出，(根左右)，
当前节点入栈，
while 栈不空:
    则出栈访问。
    右孩子入栈。
    左孩子入栈。
这样保证 先左，再右的顺序
"""
class Solution:
    def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        result=[]
        stack=collections.deque([root]) #栈是append，pop
        while stack:
            #栈不空，出栈访问
            node=stack.pop()
            result.append(node.val)
            #后进先出
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return result


"""
中序遍历：左 根 右
"""
#递归版本
class Solution:
    def InorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result=[]
        def inorder(root):
            if not root:
                return
            inorder(root.left)
            result.append(root.val)
            inorder(root.right)
        inorder(root)
        return result
#非递归版本
"""
栈，一路向左入栈，直到叶子节点。
栈顶元素出栈，访问。转向右子树。
向左入栈-->访问当前元素-->转向右子树
"""
class Solution:
    def InorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        result=[]
        stack=collections.deque([])
        node=root
        #从根节点开始一路向左入栈
        while node or stack:
            #向左入栈
            while node:
                stack.append(node)
                node=node.left
            #弹出栈顶元素，访问，转向右子树
            node=stack.pop()
            result.append(node.val)
            node=node.right
        return result


"""
后序遍历：左右根
"""
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        #给定树的根节点，返回后续遍历结果
        result=[]
        def postoerder(root):
            if not root:
                return
            postoerder(root.left)
            postoerder(root.right)
            result.append(root.val)
        postoerder(root)
        return result
"""
后续非递归版本:左，右，根。
只有当左，右孩子节点都访问完了之后才能访问根节点。或者说没有左右孩子节点时才可以访问根节点
方法：
使用一个变量prev用于记录上一个访问的节点是谁，
初始时，依然是根节点入栈，然后访问根节点（注意并没有弹出）
while 栈不空:
    if 左右孩子为空 or 左右孩子都访问完成：
        弹出栈顶元素，访问。
    else:
        右孩子不空:右孩子入栈
        左孩子不空:左孩子入栈
"""
class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        result=[]
        stack=collections.deque([root])
        prev=None#记录前一个访问的节点
        while stack:
            #访问栈顶元素
            node=stack[-1]
            #如果prev指向左孩子，且当前有右孩子，-->由于我是先右入栈，再左入栈，
            # 且前一个访问的是左孩子，说明现在是右孩子我是肯定能够访问的
            #  既包括了 根节点左右孩子都访问完的情况，又包括左孩子访问完即将访问右孩子的情况
            if (not node.left and not node.right) or (prev and (prev==node.left or prev==node.right)):
                result.append(stack.pop().val) #注意这里是val
                prev=node
            else:#还有孩子没有访问
                if node.right:
                    stack.append(node.right)
                if node.left:
                    stack.append(node.left)
        return result


"""
层次遍历：
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]
注意这里需要明确划分每一层的节点

思想：
使用BFS，队列。队列中存储还没有访问的元素。
根节点入队列。
while 队列不空：
    队头出队列。访问。
    左右孩子不空则入队列。
注意，如果需要明确划分每一层，则需要一个变量size记录当前层的节点数量。弹出一个，size-1，直到size=0，当前层遍历完了。level++；
这是直到当前遍历到哪一层的方法
"""
class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        result = []
        queue = collections.deque([root])  # append,popleft,
        # 队列不空
        while queue:
            # 记录当前层的节点
            tmp = []
            # 依次访问当前层的节点
            for i in range(len(queue)):
                # 弹出队列，访问
                node = queue.popleft()
                tmp.append(node.val)
                # 如果左右孩子不空，则入队列
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
            # 将当前层的节点加入到最终数组中
            result.append(tmp)
        return result

前序中序，前序后序，后续中序构建二叉树：

from typing import List, Optional

"""
前序+中序构造二叉树

前序：根 左子树，右子树  -->确定根节点的位置
中序：左子树 根  右子树  -->确定左右子树的节点个数范围。

根据前序遍历的第一个元素确定根节点。
到中序数组中确定根节点的位置。进而确定左右子树的范围。
这样进而可以确定前序遍历数组中左右子树的范围。通过递归构建左右子树。进而构建完成的整棵树。
"""

class TreeNode:
    def __init__(self,val=0,left=None,right=None):
        self.val=val
        self.left=left
        self.right=right

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        in_hashTable={val:index for index,val in enumerate(inorder)}
        #给定子树的前序和中序数组的范围
        def hepler(pre_start,pre_end,in_start,in_end):
            #确定递归终止条件：所有子树都构建完了，数组没有元素了
            if pre_start>pre_end or in_start>in_end:
                return None
            #确定子树根节点
            root_val=preorder[pre_start]
            root=TreeNode(root_val)

            #到中序数组中确定根的位置
            root_in_index=in_hashTable[root_val]
            #确定左右子树的范围
            #左子树节点的个数
            left_count=root_in_index-in_start

            #递归创建左右子树
            root.left=hepler(pre_start+1,pre_start+left_count,in_start,root_in_index-1)
            root.right = hepler(pre_start+left_count+1, pre_end, root_in_index+1, in_end)

            return root

        return hepler(0,len(preorder)-1,0,len(inorder)-1)


"""
中序后序构造二叉树：
中序：左子树 根节点 右子树  -->确定左右子树的节点范围
后序：左子树 右子树 根节点   -->确定根节点

跟前序+中序构造是一样的。
后序最后一个节点确定根。
到中序中找根的下标，确定左右子树的范围，进而确定后序数组中左右子树的范围。从而可以递归的构建左右子树
"""
class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        in_hashTable={val:index for index,val in enumerate(inorder)}

        def helper(post_start,post_end,in_start,in_end):
            #递归终止条件
            if post_start>post_end or in_start>in_end:
                return None

            root_val=postorder[post_end]
            root=TreeNode(root_val)

            root_in_index=in_hashTable[root_val]
            #左子树节点的个数
            left_count=root_in_index-in_start

            #递归创建左右子树 这是唯一的区别
            root.left=helper(post_start,post_start+left_count-1,in_start,root_in_index-1)
            root.right = helper(post_start+left_count, post_end-1, root_in_index+1, in_end)

            return root
        return helper(0,len(postorder)-1,0,len(inorder)-1)

"""
前序+后序构建二叉树：

前序：根节点  左子树  右子树
后序：左子树 右子树 根节点

注意：前序+后序不能唯一构造。
因为：存在多种情况：
1. 没有右子树
前序：根节点  左子树  
后序：左子树  根节点

2.没有左子树
前序：根节点  右子树
后序： 右子树 根节点

3.都有

所以你不能确定 前序序列中preorder[1]到底是位于左子树还是位于右子树，所以存在多种解。
这个题目要求只返回一种解即可。那么我们规定preorder[1]就位于左子树上。
"""
class Solution:
    def constructFromPrePost(self, preorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        po_hashTable={val:index for index,val in enumerate(postorder)}

        def helper(pre_start,pre_end,post_start,post_end):
            #递归终止条件
            if post_start>post_end or pre_start>pre_end:
                return None

            #构造根节点
            root_val=preorder[pre_start]
            root=TreeNode(root_val)

            if pre_start==pre_end:
                return root
            #根左右
            #左（左右根）右根
            #前序的第二个节点是左子树的根
            left_root_val=preorder[pre_start+1]
            #在后序中找到左子树根的位置（左子树最后一个节点）
            left_root_po_index=po_hashTable[left_root_val]#左子树最后一个节点的位置
            #确定左子树的范围
            "注意左子树的节点范围"
            left_cont=left_root_po_index-post_start+1 #注意还要算上left_root_po_index,因为这是左子树的根，当然在左子树中

            #递归创建左右子树 这是唯一的区别
            root.left=helper(pre_start+1,pre_start+left_cont,post_start,left_root_po_index)
            root.right = helper(pre_start+left_cont+1,pre_end,left_root_po_index+1,post_end-1)

            return root
        return helper(0,len(preorder)-1,0,len(postorder)-1)

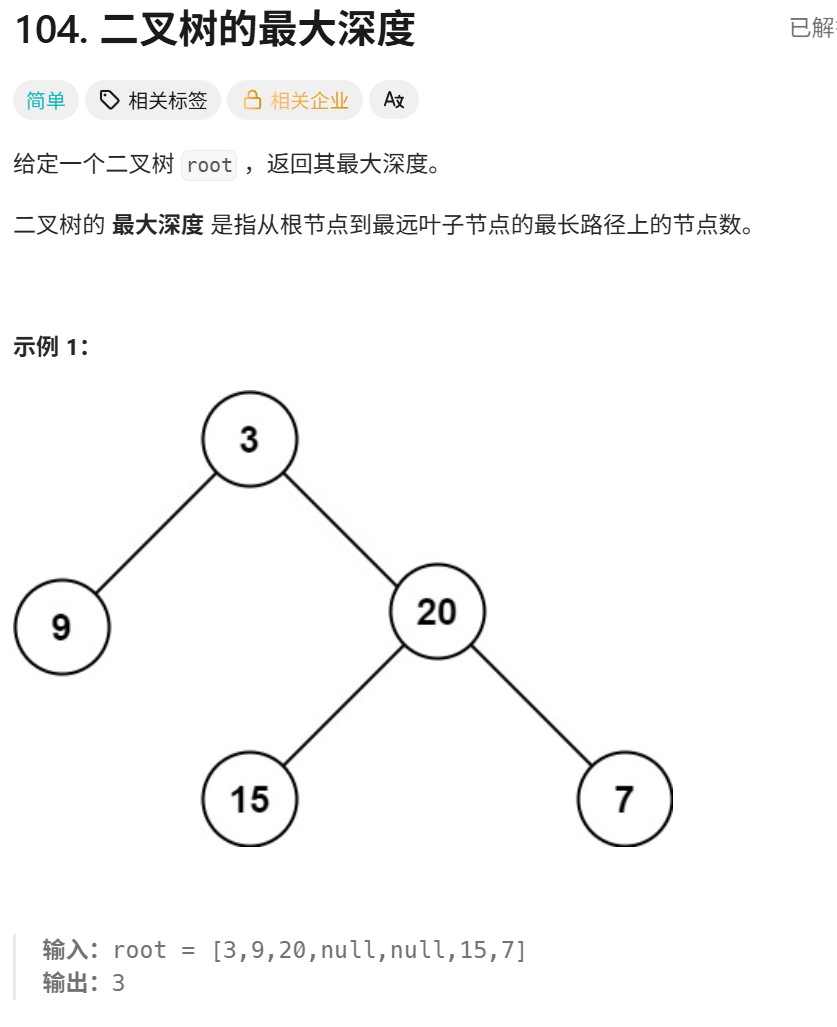
# Definition for a binary tree node.
from typing import Optional


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

'''
二叉树的最大深度是指从根节点到最远叶子节点的最长路径上的节点数。

二叉树的深度是从根节点开始算起，依次往下深度为1，2，3；
二叉树的深度（从上到下）等于二叉树的层次（从左到右）；最大深度为最大层次。
二叉树的高度（从下到上）是从节点算起，叶子节点高度为1，依次往上。

递归求解最大深度：
递归左子树的最大高度，递归右子树的最大高度，根节点的最大深度=max(左右子树最大高度)+1

！！高度是从叶子开始算；深度是从根开始算

递归终止条件：节点为空；高度为0

'''
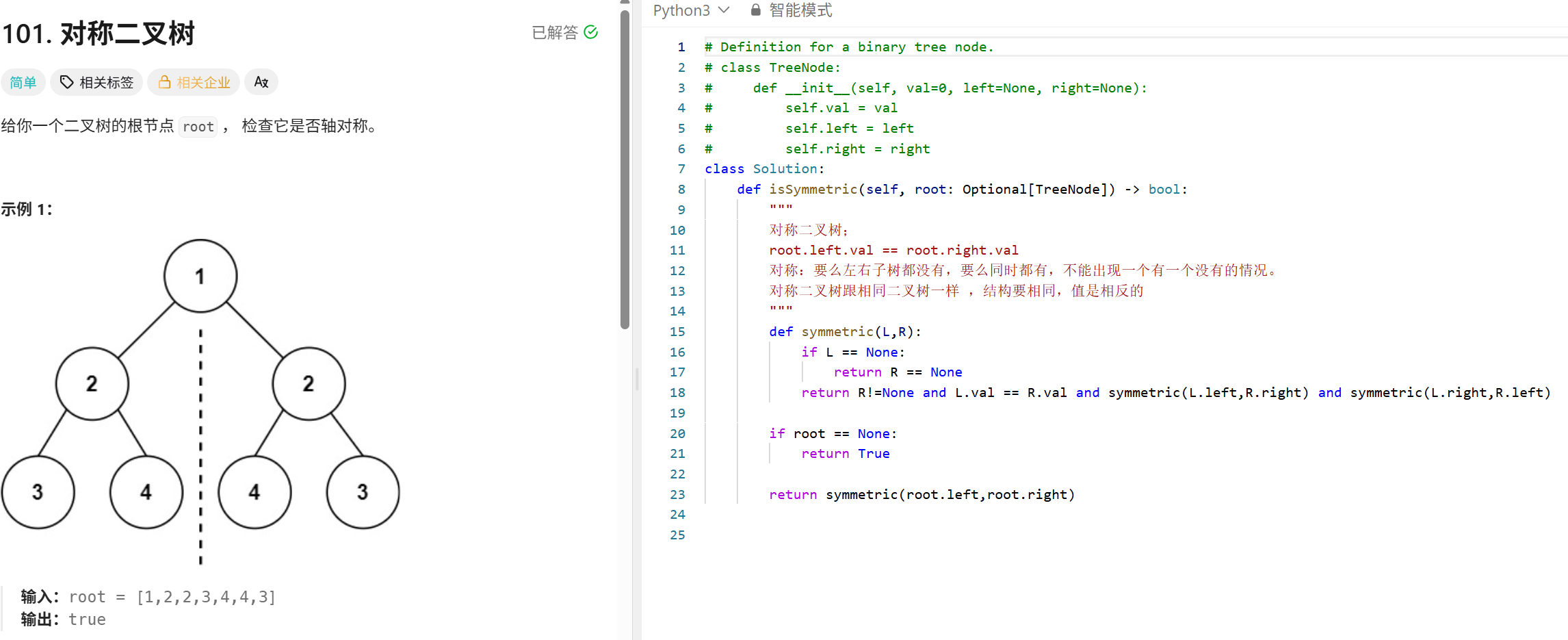
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        if root==None:
            return 0

        leftHeight=self.maxDepth(root.left)
        rightHeight=self.maxDepth(root.right)
        rootHeight=max(leftHeight,rightHeight)+1
        return rootHeight
        #后序遍历
    
'''
迭代版本：动态维护一个值
（层次遍历的思想）
初始化一个队列，每一层入队列，深度+1；直到遍历完所有层，得到最大深度。

初始化空队列，根节点入队列，depth=0
队列不空：
遍历队列中的每一个值，出队列，若左右子树不空，则入队列。
每一层遍历完之后，depth++

tips:可以用一个额外的数组tmp来存储下一层的子节点，当前层节点全部遍历完之后，更新队列（让队列指向tmp）

'''


def maxDepth(self, root: Optional[TreeNode]) -> int:
    if root is None:
        return 0
    queue,depth=[root],0
    while queue:
        tmp=[]  #如果我用了一个额外的数组来更新队列，那就不需要出队列了
        for node in queue:
            if node.left: tmp.append(node.left)
            if node.right: tmp.append(node.right)
        queue=tmp
        depth+=1
    return depth

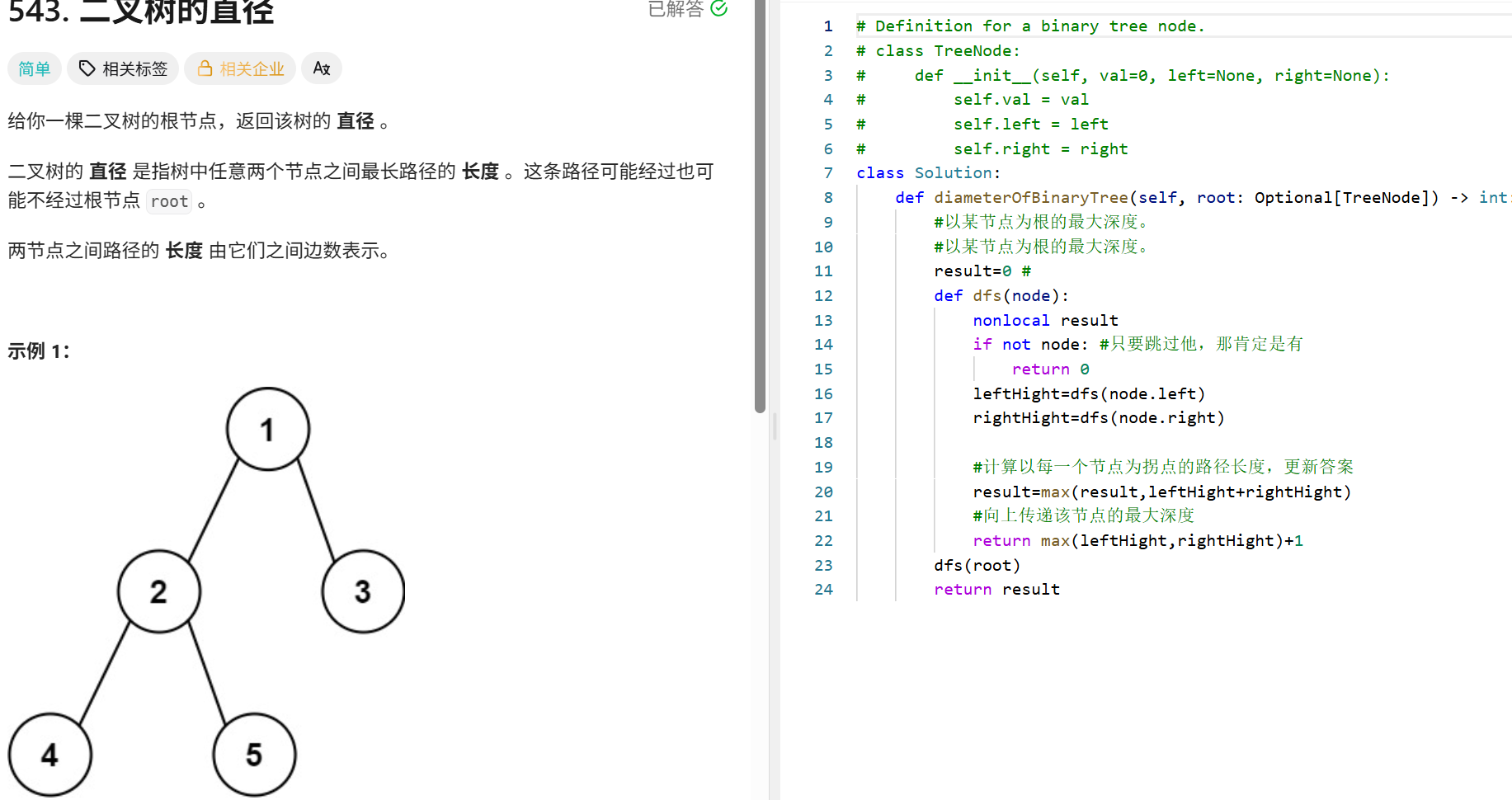
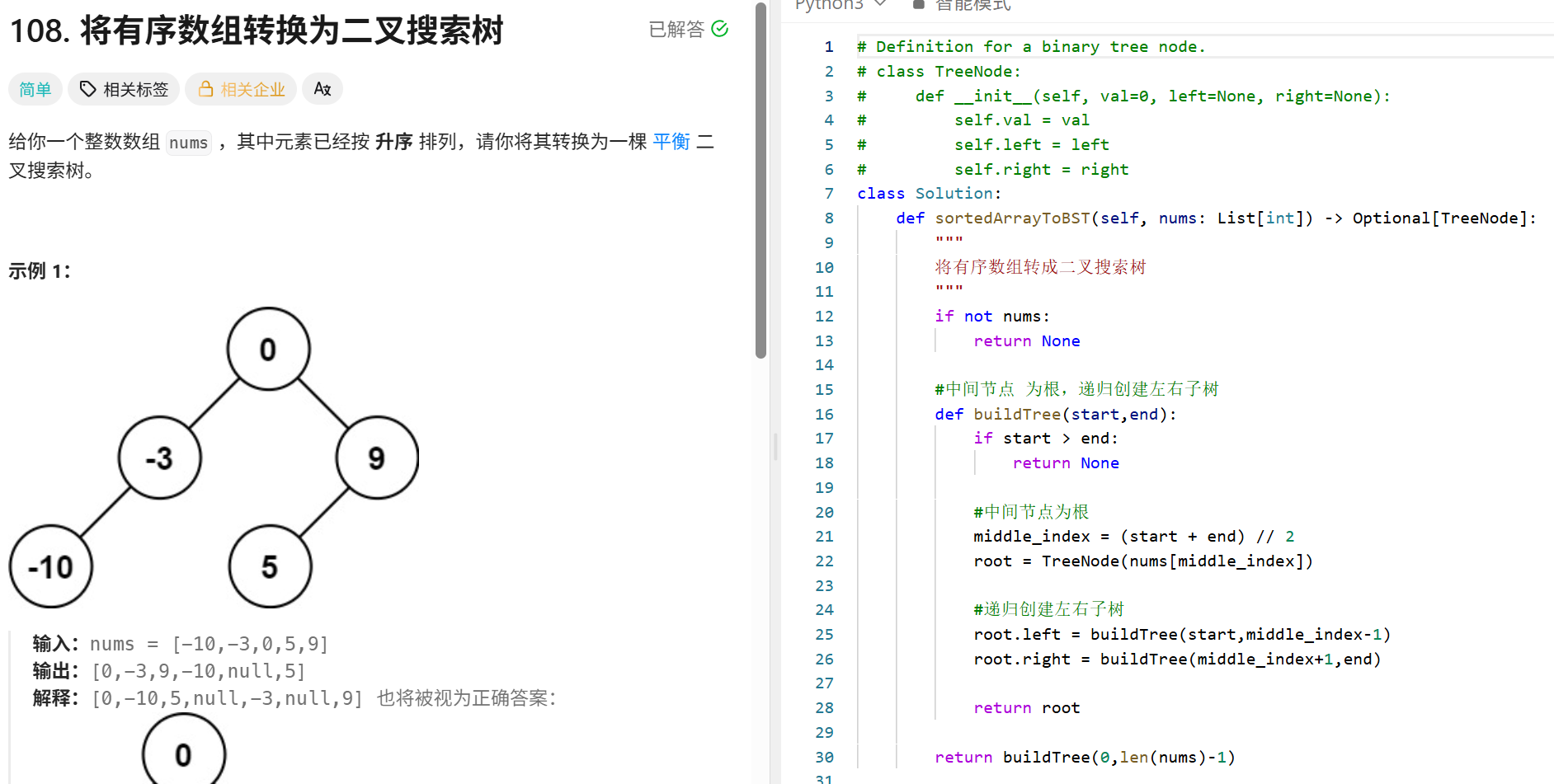
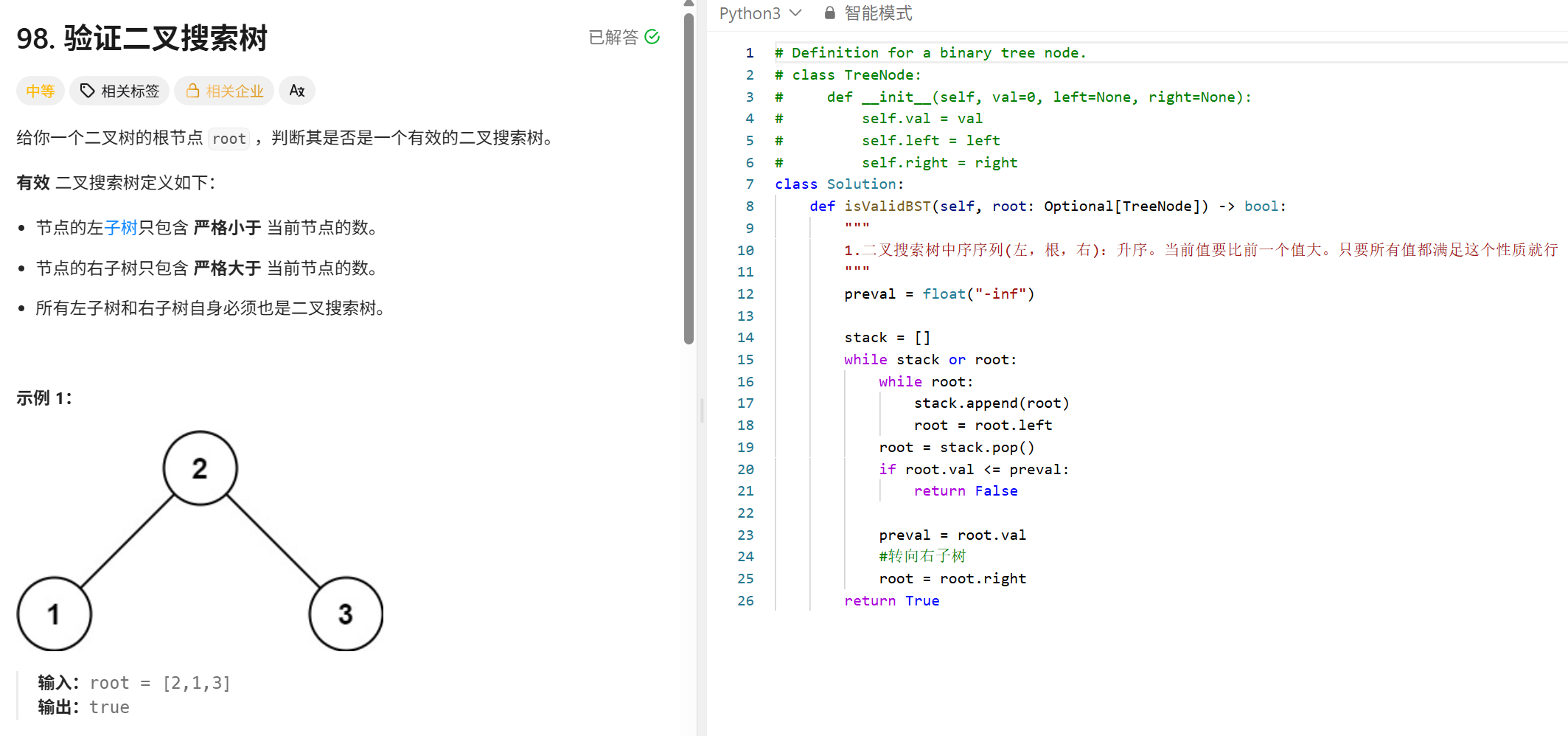
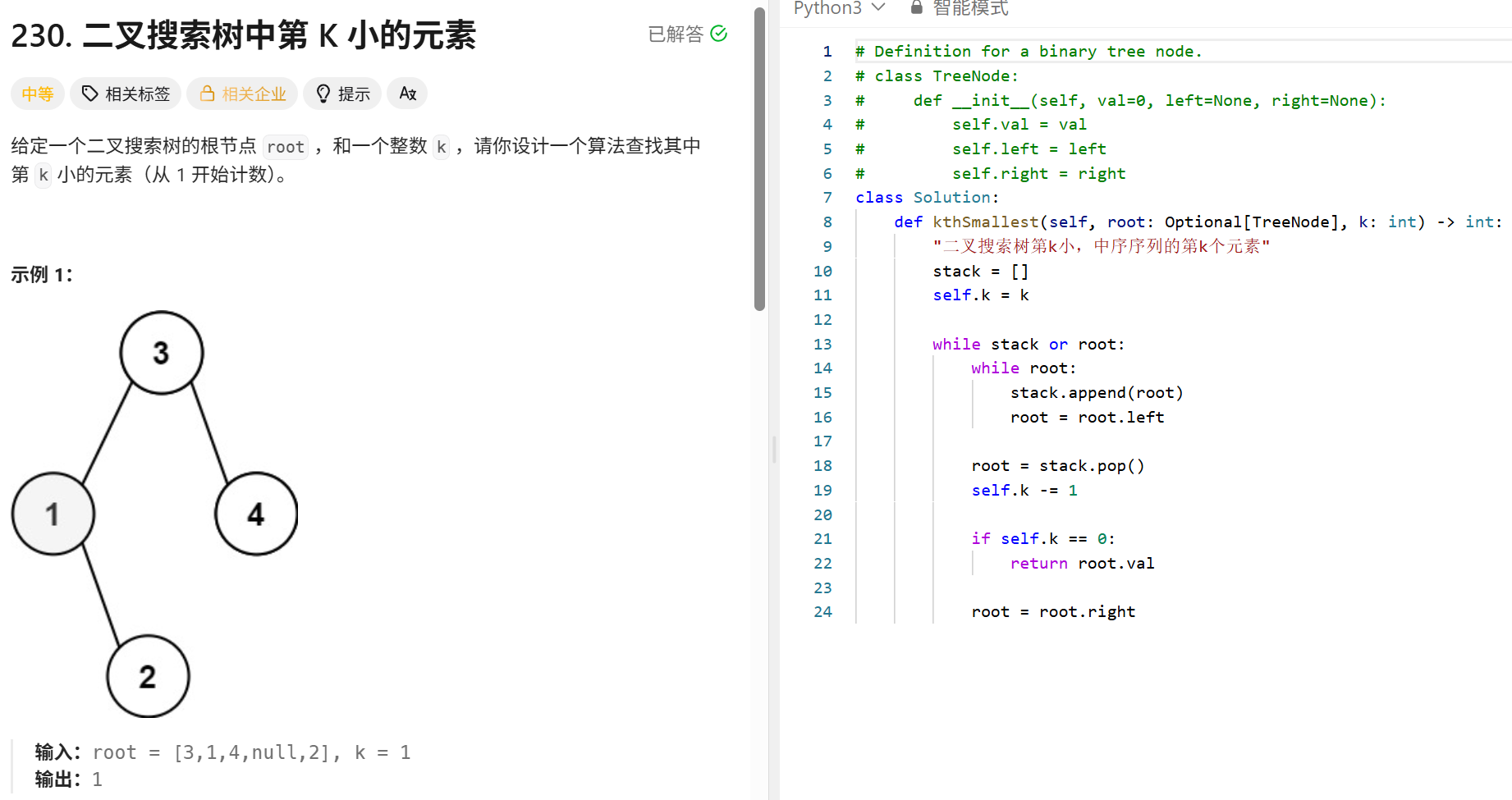
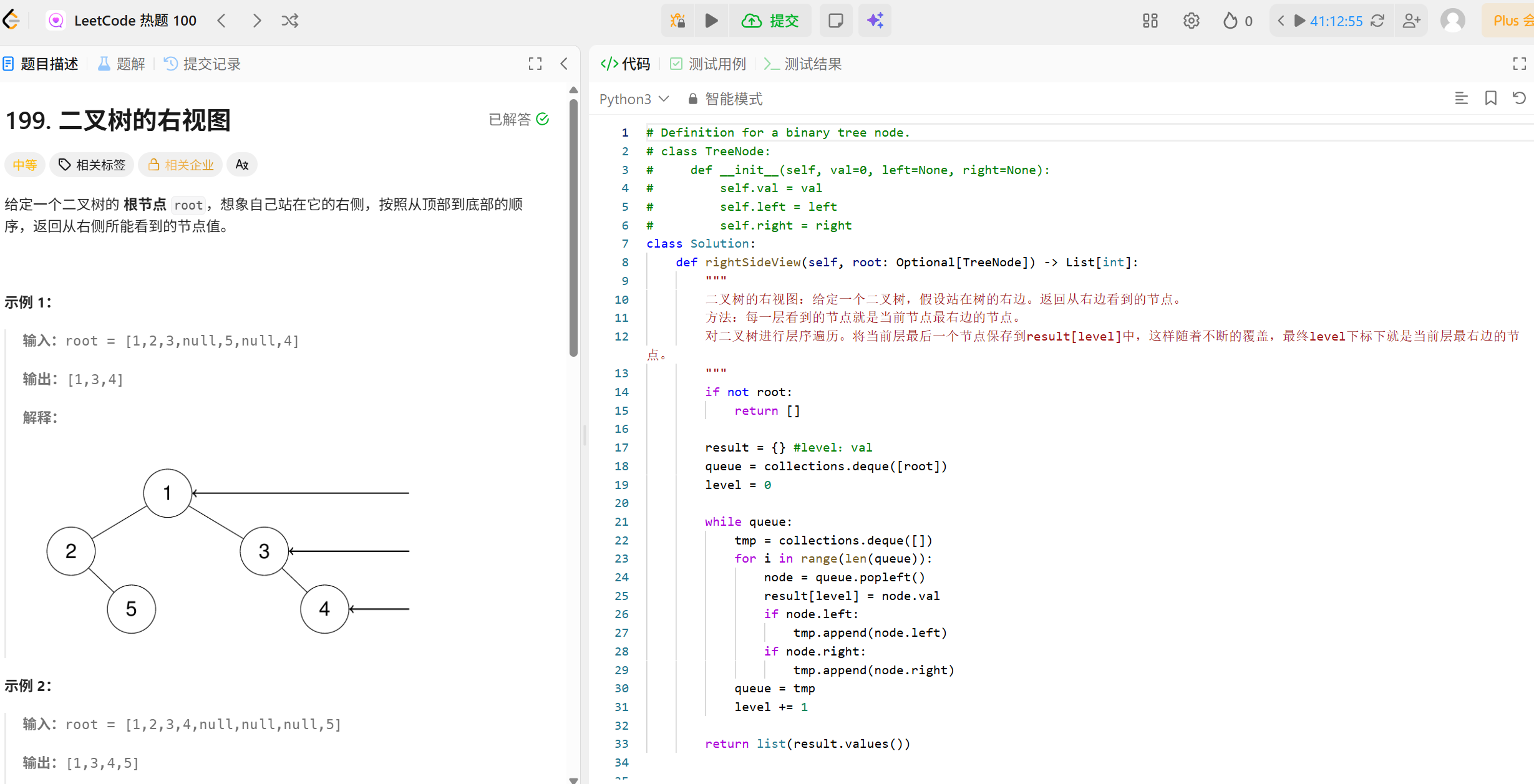
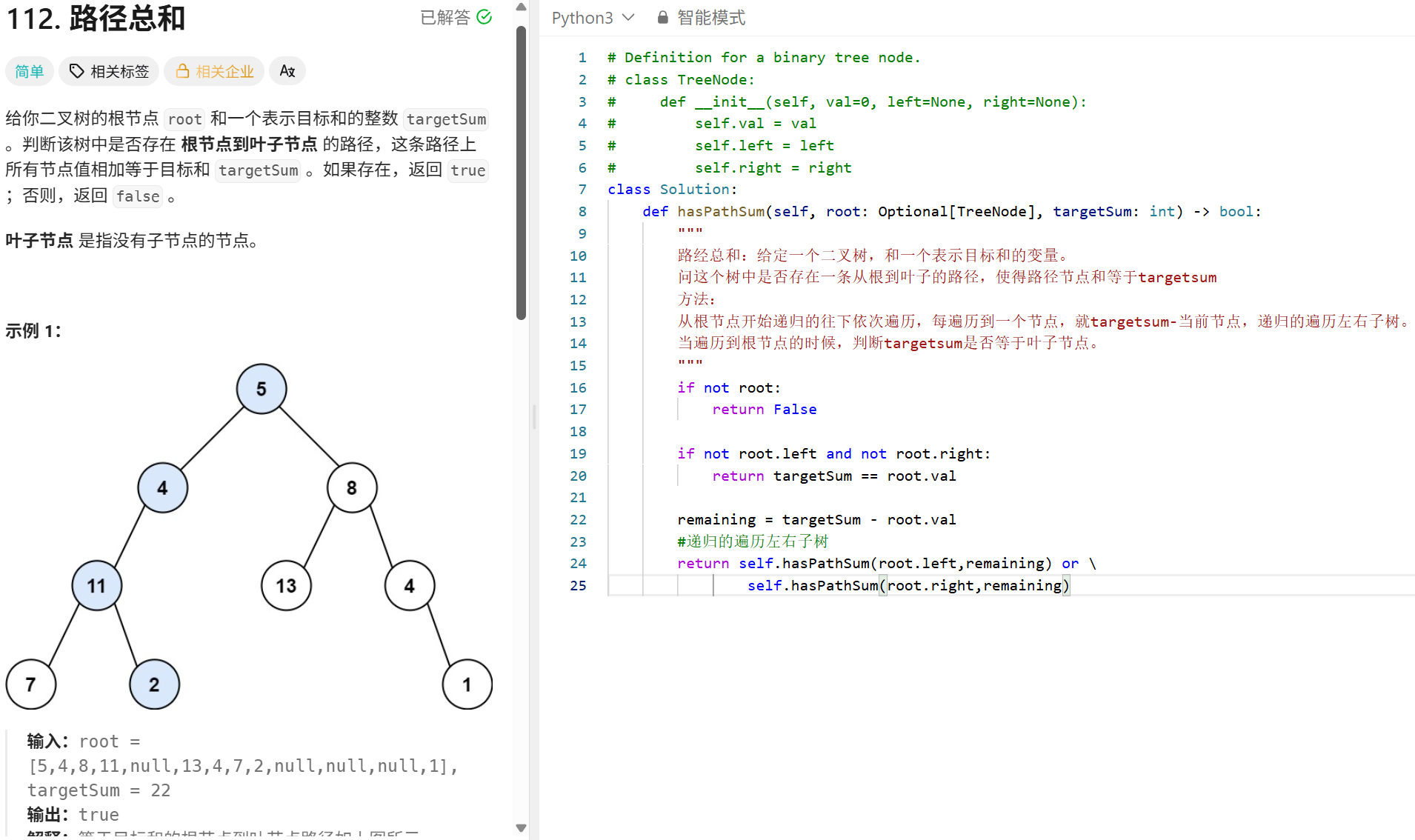
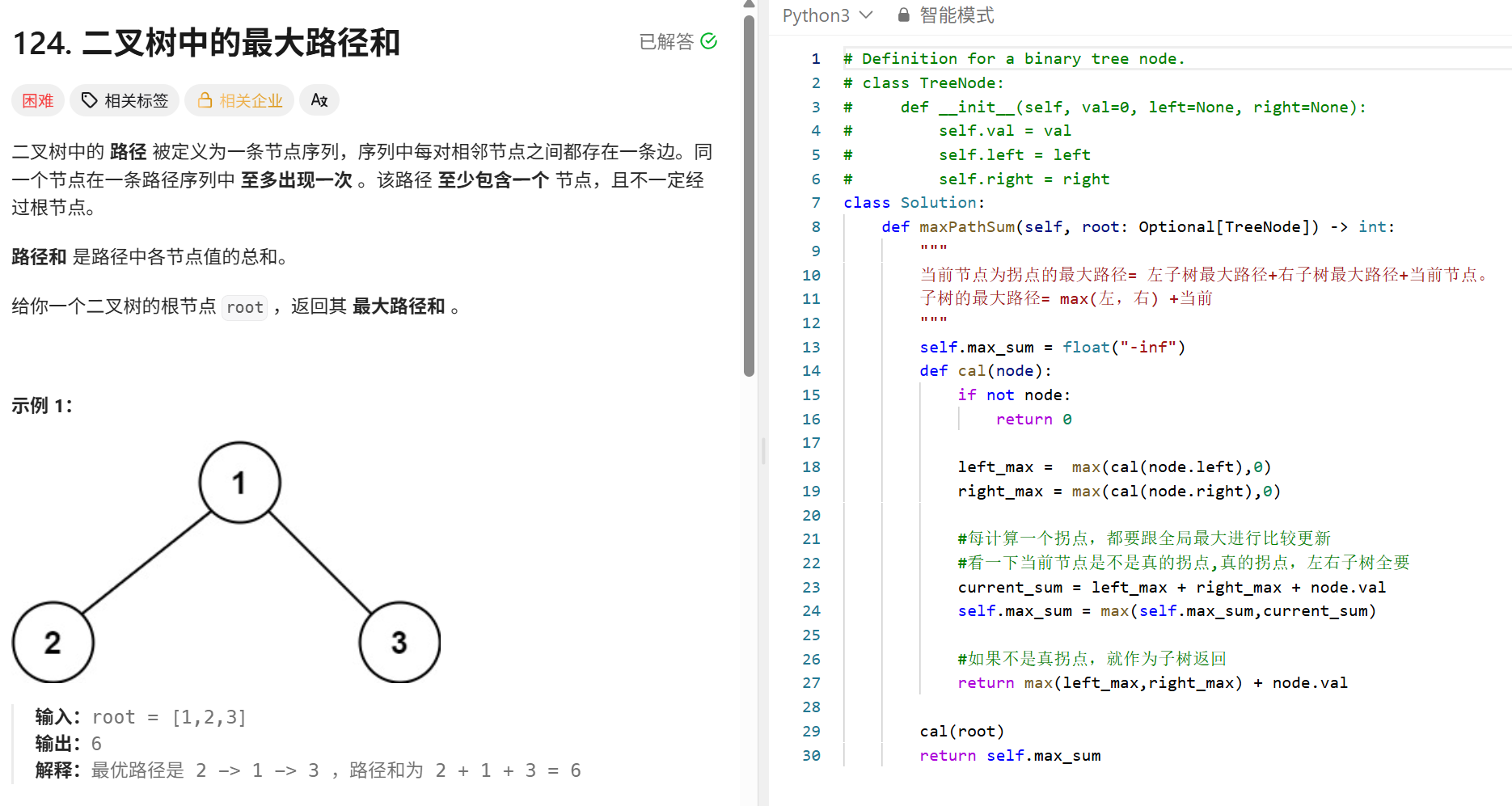
Transformer(MHA):

import torch
import torch.nn as nn
import numpy as np
import math

from einops import rearrange

"手工实现"
class Config(object):
    def __init__(self):
        self.vocab_size = 6

        self.d_model = 20
        self.n_heads = 2

        assert self.d_model % self.n_heads == 0
        self.dim_k  = self.d_model % self.n_heads
        self.dim_v = self.d_model % self.n_heads

        self.padding_size = 30 #统一到长度30
        self.UNK = 0
        #从分词器的词汇表中获取特殊标记PAD的索引。
        self.pad_index = tokenizer.vocab('[PAD]')

        self.N = 6
        self.p = 0.1
config = Config()

#Embedding部分 (输入[batch,seq_len]-->[batch,seq_len,d_model]  短补长齐)
class Embedding(nn.Module):
    def __init__(self,vocab_size):
        super(Embedding, self).__init__()
        # 一个普通的 embedding层，我们可以通过设置padding_idx=config.PAD 来实现论文中的 padding_mask
        """当你创建一个 Embedding 层并设置 padding_idx 参数时，PyTorch 会在内部的权重矩阵中，将该索引对应的向量初始化为零。"""
        self.embedding=nn.Embedding(vocab_size,config.d_model,padding_idx=config.pad_index)
        "对但序列进行填充<PAD>,将序列统一到最长序列的那个长度；（但是最长序列不一定是想要的长度，想要的长度是config.padding_size）而<PAD>在embedding中是0"

    def forward(self,x):
        for i in range(len(x)):
            if len(x[i])< config.padding_size:#如果最长序列比这个还短，那肯定需要再次填充
                x[i].extend([config.UNK]*(config.padding_size-len(x[i])))  #短补
            else:
                x[i]=x[i][:config.padding_size]#长截

        x=self.embedding(torch.tensor(x))
        # 注意这里不是矩阵乘法，而是索引操作，所以padding_size可以不等于vocab_size.(详情见Transformer.md
        return x

#手工实现位置编码
class Positional_Encoding(nn.Module):
    def __init__(self,d_model):
        super(Positional_Encoding,self).__init__()
        self.d_model=d_model

    def forward(self,seq_len,embedding_dim):
        #根据位置编码的公式计算位置编码矩阵
        positional_encoding=np.zeros((seq_len,embedding_dim))
        for pos in range(positional_encoding.shape[0]):
            for i in range(positional_encoding.shape[1]):
                positional_encoding[pos][i] = math.sin(pos/(10000**(2*i/self.d_model))) if i % 2 == 0 \
                    else math.cos(pos/(10000**(2*i/self.d_model)))
        return torch.from_numpy(positional_encoding)

#多自头注意力
class MultiHeadSelfAttention(nn.Module):
    def __init__(self, d_model, heads=8):
        super(MultiHeadSelfAttention, self).__init__()

        self.heads = heads
        self.dim_k = d_model //self.heads
        self.to_q = nn.Linear(d_model, d_model, bias=True)
        self.to_kv = nn.Linear(d_model, d_model * 2, bias=True)
        self.W_0 = nn.Linear(d_model, d_model, bias=False)
        self.scale_factor = self.dim_k ** -0.5

    def generate_mask(self, seq_len):
        # 生成 causal mask（防止未来信息泄漏）
        mask = torch.tril(torch.ones(seq_len, seq_len)).bool()  # shape [L, L]
        return mask  # bool 类型 mask（True 代表允许，False 为屏蔽）

    def forward(self, x, y, requires_mask=False):
        # Q from y
        q = self.to_q(y)  # [b, t, dim_k * heads]
        q = rearrange(q, "b t (h d) -> b h t d", h=self.heads)
        kv = self.to_kv(x)  # [b, t, 2 * dim_v * heads]
        k,v= tuple(rearrange(kv, "b t (two h d) -> two b h t d", two=2, h=self.heads))

        scores = torch.einsum('b h i d , b h j d -> b h i j', q, k) * self.scale_factor

        if requires_mask:
            seq_len = y.shape[1]
            mask = self.generate_mask(seq_len).to(x.device)  # [L, L]
            mask = rearrange(mask, "i j -> 1 1 i j")  # 扩展为 [1, 1, L, L] 以匹配 scores
            scores = scores.masked_fill(mask == 0, float('-inf')) #上三角置为 -∞

        attention = torch.softmax(scores, dim=-1)
        # attention 输出： [b, h, i, j] x [b, h, j, d] -> [b, h, i, d]
        out = torch.einsum('b h i j , b h j d -> b h i d', attention, v)
        # concat 多头输出 -> [b, t, h * d]
        out = rearrange(out, "b h t d -> b t (h d)")
        # 输出线性层
        return self.W_0(out)
"FeedForward"
#就是两层Linear
"""
Linear1
Relu
Linear2
"""
class FeedForward(nn.Module):
    def __init__(self,input_dim,hidden_dim=2048):#input_dim是512
        super(FeedForward,self).__init__()
        self.L1=nn.Linear(input_dim,hidden_dim)
        self.L2=nn.Linear(hidden_dim,input_dim)

    def forward(self,x):
        output=nn.ReLU((self.L1(x)))
        output=self.L2(output)
        return output

"Add & Norm"
#即残差链接和LayerNorm  LayerNorm(x+Dropout(Sublayer(x))) ;此外还有dropout操作
class Add_Norm(nn.Module):
    def __init__(self):
        super(Add_Norm).__init__()
        self.dropout=nn.Dropout(config.p)
    def forward(self,x,sub_layer,**kwargs):
        #LayerNorm对每个符号的所有特征进行归一化。
        layer_norm=nn.LayerNorm(x.shape[-1])#就是dim的维度大小

        out=layer_norm(x+self.dropout(sub_layer(x,**kwargs)))
        return out

"将上述部分拼接为Encoder："
"""
Embedding
positional_embedding
multihead_atten
feed_forward
add_norm
"""
class Encoder(nn.Module):
    def __init__(self):
        super(Encoder,self).__init__()
        self.Positional_embedding=Positional_Encoding(config.d_model)
        self.Multi_atten=MultiHeadSelfAttention(config.d_model,config.n_heads)
        self.FeedForward=FeedForward(config.d_model)
        self.Add_Norm=Add_Norm()

    def forward(self,x):
        x=x+self.Positional_embedding(x.shape[1],config.d_model)
        output=self.Add_Norm(x,self.Multi_atten,y=x) #encoder下 x=y
        output=self.Add_Norm(output,self.FeedForward)

        return output

"Decoder"
class Decoder(nn.Module):
    def __init__(self):
        super(Decoder,self).__init__()
        self.Positional_embedding=Positional_Encoding(config.d_model)
        self.Multi_atten=MultiHeadSelfAttention(config.d_model,config.n_heads)
        self.FeedForward=FeedForward(config.d_model)
        self.Add_Norm=Add_Norm()

    def forward(self,x,encoder_output):
        x=x+self.Positional_embedding(x.shape[1],config.d_model)
        #一共有三个sub_layer (残差链接
        #第一个sub_layer
        output=self.Add_Norm(x,self.Multi_atten,y=x,requires_mask=True)
        #第二个sub_layer        KV                          Q
        output=self.Add_Norm(encoder_output,self.Multi_atten,y=output,requires_mask=False)
        #第三个sub_layer
        output=self.Add_Norm(output,self.FeedForward)

        return output

"组装Transformer"
#6个Encoder和Decoder
class Transformer_layer(nn.Module):
    def __init__(self):
        super(Transformer_layer,self).__init__()
        self.encoder=Encoder()
        self.decoder=Decoder()

    def forward(self,x):
        x_input,x_output=x
        encoder_output=self.encoder(x_input)
        decoder_output=self.decoder(x_output,encoder_output)
        return (encoder_output,decoder_output)

class Transformer(nn.Module):
    def __init__(self,N,vocab_size,output_dim):
        #N=6
        super(Transformer,self).__init__()
        self.input_embedding=Embedding(vocab_size=config.vocab_size)
        self.output_embedding=Embedding(vocab_size=config.vocab_size)

        self.output_dim=output_dim

        #这个是分类头
        self.linear=nn.Linear(config.d_model,self.output_dim)
        self.softmax=nn.Softmax(dim=-1)

        #构建6块8头
        self.model=nn.Sequential(*[Transformer_layer() for _ in range(N)])

    def forward(self,x):
        #所以Transformer的数src和tgt是一起输入的
        x_input,x_output=x
        x_input=self.input_embedding(x_input)
        x_output=self.output_embedding(x_output)
        _,output=self.model((x_input,x_output))
        output=self.linear(output)
        output=self.softmax(output)

        return output

GQA:

import torch
import torch.nn as nn
from einops import rearrange

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads, group_num=4):
        super(MultiHeadAttention, self).__init__()
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.group_num = group_num
        self.head_dim = embed_dim // num_heads
        self.wq = nn.Linear(embed_dim, embed_dim)
        self.wkv = nn.Linear(embed_dim, self.group_num * self.head_dim *2)
        self.wo = nn.Linear(embed_dim, embed_dim)
        self.scale = self.head_dim ** -0.5  # 缩放因子提前计算好

    def forward(self, x,y, mask=None):
        B, L, _ = y.size()
        # Q: [B, L, H * D], K/V: [B, L, G * D]
        q = self.wq(y)
        kv = self.wk(x)
        # Q 拆成多头: [B, H, L, D]
        q = rearrange(q, 'b l (h d) -> b h l d', h=self.num_heads)
        # K/V 拆成多组: [B, G, L, D]
        k,v = tuple(rearrange(kv, 'b l (g d two) -> two b g l d', two=2,g=self.group_num))
        # 将 K/V 按组 expand 成多头：每组分配 H/G 个头
        # K/V -> [B, H, L, D]
        "需要确定，每一组有多少个Q。（把heads这么多头分成gropu组，每组有多少个头），现在就需要把每组的K,V扩展成这些头"
        heads_per_group = self.num_heads // self.group_num
        k = k[:, :, None, :, :].expand(B, self.group_num, heads_per_group, L, self.head_dim)
        v = v[:, :, None, :, :].expand(B, self.group_num, heads_per_group, L, self.head_dim)
        k = rearrange(k, 'b g h l d -> b (g h) l d')
        v = rearrange(v, 'b g h l d -> b (g h) l d')
        # Attention score: [B, H, Q_len, K_len]
        scores = torch.matmul(q, k.transpose(-2, -1)) * self.scale
        if mask is not None:
            mask = mask.unsqueeze(1)  # [B, 1, Q_len, K_len]
            scores = scores.masked_fill(mask == 0, float('-inf'))
        attn = torch.softmax(scores, dim=-1)
        out = torch.matmul(attn, v)  # [B, H, L, D]
        # 合并多头: [B, L, H * D]
        out = rearrange(out, 'b h l d -> b l (h d)')
        out = self.wo(out)
        return out

MQA:

import torch
import torch.nn as nn
from einops import rearrange

class MultiHeadAttention(nn.Module):
    def __init__(self, embed_dim, num_heads):
        super(MultiHeadAttention, self).__init__()
        self.num_heads = num_heads
        self.head_dim = embed_dim // num_heads
        self.wq = nn.Linear(embed_dim, embed_dim)
        self.wk = nn.Linear(embed_dim, self.head_dim)
        self.wv = nn.Linear(embed_dim, self.head_dim)
        self.wo = nn.Linear(embed_dim, embed_dim)

    def forward(self, x,y, mask=None):
        # q: [B, L, E] → [B, L, H, D] → [B, H, L, D]
        q = self.wq(y)
        q = rearrange(q, "b l (h d) -> b h l d", h=self.num_heads)
        k = self.wk(x)  # [B, L, D]
        v = self.wv(x)  # [B, L, D]
        # 添加一个 head 维度：→ [B, 1, L, D]
        k = rearrange(k, "b l d -> b 1 l d")
        v = rearrange(v, "b l d -> b 1 l d")
        # attention scores: [B, H, L, D] x [B, 1, D, L] → [B, H, L, L]
        scores = torch.matmul(q, k.transpose(-2, -1)) / self.head_dim ** 0.5
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))
        attn = torch.softmax(scores, dim=-1)
        # attention output: [B, H, L, L] x [B, 1, L, D] → [B, H, L, D]
        out = torch.matmul(attn, v)
        # 合并多头: [B, H, L, D] → [B, L, H * D]
        out = rearrange(out, "b h l d -> b l (h d)")
        return self.wo(out)

RMSNorm:

import torch
import torch.nn as nn


class RMSNorm(nn.Module):
    def __init__(self,d_model,eps=1e-8):
        self.eps=eps
        self.scale=nn.Parameter(torch.ones(d_model))
        self.bias=nn.Parameter(torch.zeros(d_model))

    def forward(self,x):
        #计算均方根
        rms=torch.sqrt(torch.mean(x.pow(2),dim=-1,keepdim=True))

        #数据归一化
        x_norm=x/(rms+self.eps)
        #缩放和平移
        return x_norm*self.scale+self.bias

RoPE:

"1.拆分向量，二维旋转"
import torch
def rotate_half(x):
    "对最后一个维度进行二维旋转，（x1,x2）-->(-x2,x1)"
    x1,x2=x[...,:x.shape[-1]//2],x[...,x.shape[-1]//2:]#获取前一半和后一半
    return torch.cat((-x2,x1),dim=-1)

"计算旋转位置频率矩阵，用于后序sin和cos的计算"
"""
get_rope_frequencies 的作用是计算 RoPE 旋转编码所需的频率矩阵，
用于在不同维度上施加不同的旋转角度，
使得 token 位置信息能够通过正弦和余弦变换隐式编码进去。
它确保低维部分变化快，高维部分变化慢，从而增强模型对相对位置的感知能力。
"""
def get_rope_frequencies(dim,seq_len,base=10000):
    "1.按照维度的大小计算theta频率" #低维频率大，高维频率小。
    theta=1.0/(base**(torch.range(0,dim,2).float() / dim))
    "2.计算位置编码角度"
    positions=torch.arange(seq_len).unsqueeze(1) #二维
    "计算每个位置和每个频率的乘积"
    freqs=torch.einsum('i,j->ij',positions,theta) #（seq_len,dim//2）
    return torch.cat([freqs,freqs],dim=-1)

"应用旋转位置编码"
def apply_rope_emb(x,freqs):
    return (x*freqs.cos())+(rotate_half(x)*freqs.sin())

CE:

import torch

def softmax(x):
    """
    x：（batchsize，num_classes）
    softmax(z)=exp(z)/sumexp(z)
    """
    exp_x=torch.exp(x-torch.max(x,dim=-1,keepdim=True).values)
    return exp_x/torch.sum(exp_x,dim=1,keepdim=True)




"对概率取对数后与实际类别的one-hot编码进行逐位相乘再求和的操作，最后记得加个负号"
def cross_entropy_loss(y_probs,y_true):
    """
    :param z:模型输出值 (batchsize,num_classes)
    :param q: 真实标签 (batchsize,)
    :return：平均交叉熵损失
    """
    probs=softmax(y_probs)
    """
    -sum(logqi)
    """
    #找到真实标签对应的概率
    correct_q=probs[torch.arange(y_probs.shape[0]),y_true]#一个向量
    loss= -torch.log(correct_q)
    return torch.mean(loss)

InfoNCE:

import torch
import torch.nn as nn
"假设就是图文的InfoNCE损失"
class InfoNCE(nn.Module):
    def __init__(self,temperature=0.1):
        super().__init__()
        self.temperature=temperature

    def forward(self,image_feature,text_feature):

        similarity=(image_feature@text_feature.T)/self.temperature
        #定义正样本索引
        labels=torch.arange(image_feature.shape[0])
        image_loss=self.cross_entropy(similarity,labels)
        text_loss=self.cross_entropy(similarity.T,labels.T)
        total_loss = (image_loss + text_loss) / 2
        return total_loss.item()

    def cross_entropy(self,similarity,labels):
        probs = self.softmax(similarity)
        """
        -sum(logqi)
        """
        # 找到真实标签对应的概率
        correct_q = probs[torch.arange(similarity.shape[0]), labels]  # 一个向量
        loss = -torch.log(correct_q)

        return torch.mean(loss)

    def softmax(self,x):
        """
        softmax=exp(x)/sigmaexp(x)
        """
        exp_x=torch.exp(x-torch.max(x,dim=-1,keepdim=True).values)
        return exp_x/torch.sum(exp_x,dim=1,keepdim=True)

贪心：

…贪心的想获取所有代码

etc…
last but not least：
好牛马求内推。技术栈：
•多模态：精通 CLIP、BLIP-2 、LlaVA等多模态模型结构，具备实际调研与应用经验。
•语言模型与微调：了解 LLaMA、Qwen 等主流架构，熟悉 LoRA、QLoRA、P-Tuning 等微调技术。
•强化学习：掌握 PPO 、DPO、GRPO、GSPO等主流强化学习算法，具有相关应用经验。
•AI Agent：熟悉 LangChain、LlamaIndex使用及RAG的工作原理和向量数据库(Chroma，FAISS)。